[b]Contenido[/b][br][br]- Conceptos[br][br]- Elipse con eje focal horizontal[br][br]- Elipse con eje focal vertical[br][br]- Otro procedimiento de construcción de la elipse[br][br][br][b]Elipse[br][/b][br]Es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es una constante: [math]distancia\left(F_1P\right)+distancia\left(PF_2\right)=2a[/math]. La constante es [b]2a[/b] y equivale a la [b]medida del eje mayor[/b] de la elipse.

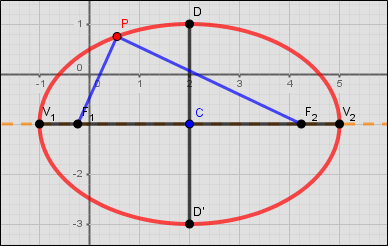
Cualquiera que sea la orientación de la elipse, se tienen los siguientes elementos:[br][br][b]Centro, C = (h, k)[/b]: Es el puto de intersección entre el eje mayor y el eje menor. Es el punto medio de cada uno de los dos ejes de la elipse. También es el punto de simetría de la elipse.[br][br][b]Eje mayor, [math]V_1V_2[/math][/b]: Es el segmento de mayor distancia entre dos puntos opuestos de la elipse. Contiene los dos vértices y los dos focos de le elipse. [br][br]La longitud del [b]eje mayor[/b] es [b]2a[/b]. Por lo tanto [b]a[/b] es la longitud del [b]semieje mayor[/b]. Equivale a la distancia [math]CV_1[/math] o [math]CV_2[/math]. [br][br][b]Eje menor, [math]DD'[/math][/b]: Es el segmento mediatriz del eje mayor. Sus extremos son puntos opuestos de la elipse.[br][br]La longitud del [b]eje menor[/b] es [b]2b[/b]. Por lo tanto [b]b[/b] es la longitud del [b]semieje menor[/b].[br][br][b]Focos, [math]F_1[/math][/b] y [math]F_2[/math]: Son dos puntos fijos de la elipse que hacen que la suma de las distancias de ellos a un punto de la elipse sea una constante. Son simétricos al centro de la elipse y se ubican en el eje mayor.[br][br][b]Eje focal[/b]: Es la recta que pasa por el centro y contiene los focos y los vértices de la elipse.[br][br][b]Semidistancia focal, c[/b]: Es la distancia entre el centro y uno cualquiera de los focos, es decir, la distancia [math]CF_1[/math] o [math]CF_2[/math]. [br][br][b]Relación entre semieje mayor, semieje menor y semidistancia focal[/b]:[br][br]La relación es pitagórica: [math]\left(semiejemayor\right)^2=\left(semiejemenor\right)^2+\left(semidistanciafocal\right)^2[/math][br][br] [math]a^2=b^2+c^2[/math] [math]\Longrightarrow[/math] [math]c=\sqrt{\left(a^2-b^2\right)}[/math][br] [br][b]Excentricidad, [math]\epsilon[/math][/b]: Es la razón entre la semidistancia focal y el semieje mayor. [math]\epsilon=\frac{c}{a}[/math] Su valor se encuentre entre cero y uno. [br][br]A continuación se presentar tres applets con una metodología similar a los applets de la parábola.[br][br]- Elipse con eje focal horizontal[br][br]- Elipse con eje focal vertical[br][br]- Otro procedimiento de construcción de la elipse[br][br][br][b]Applet 1. Elipse con eje focal horizontal[br][br][/b]- Dar los valores [b]h, k, a, b[/b]. Tenga en cuenta que [b]a > b[/b]. Se puede hacer en las casillas de entrada o con los deslizadores.[br][br]- Activar [b]Centro, eje mayor, vértices, eje menor [/b]y [b]focos[/b]. La aplicación calcula automáticamente el valor de [b]c[/b].

- Activar [b]proceso de construcción[/b]. Se visualiza el proceso de construcción: El punto [b]P[/b] es un punto de la elipse. Activando el rastro y desplazando el punto [b]A[/b] sobre la circunferencia generatriz, [b]P[/b] deja la huella que es la elipse que cumple las condiciones definidas al comienzo del applet. Se puede comprobar si se activa [b]gráfica[/b].[br][br]- Activar [b]radios vectores[/b], segmentos [math]F_1P[/math] y [math]PF_2[/math][br][br]- Activar [b]Comprobar definición[/b]. Se muestra una demostración geométrica y la comprobación mediante una tabla de valores: las medida de cada radio vector varía pero su suma siempre es [b]2a[/b].[br][br]Otra comprobación se obtiene cuando [b]P[/b] coincide con [math]V_1[/math]. En este caso [math]PF_1=V_1F_1=F_2V_2[/math] y por lo tanto la suma de los dos radio vectores equivale a la distancia entre vértices, la cual es [b]2a[/b].[br][br]- Activar [b]excentricidad[/b]. Se observa que siempre está entre cero y uno. A medida que [b]b[/b] se acerca a [b]a[/b], [b]c[/b] se acerca a cero. Cuando esto sucede, los dos focos coinciden con el centro y la elipse se convierte en una circunferencia. Por eso se puede afirmar que la circunferencia es un caso particular de la elipse.[br][br]- Activar [b]ecuación canónica[/b]. Cuando el eje focal es horizontal la ecuación es de la forma [math]\frac{\left(x-h\right)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1[/math][br][br]Un ejemplo: Si una elipse tiene su eje focal horizontal y [b]C = (2,-1)[/b], [b]a = 3[/b], [b]b = 2[/b], la ecuación canónica es [math]\frac{\left(x-2\right)^2}{9}+\frac{\left(y+1\right)^2}{4}=1[/math] .[br][br]Otros datos que se pueden obtener son:[br][br]- semidistancia focal, [math]c=2.24[/math][br][br]- Excentricidad, [math]\epsilon=0.75[/math] [br][br][i]Observación: Si [b]h = 0[/b] y [b]k = 0[/b] se tiene que el centro de la elipse es el origen del sistema de coordenadas y la ecuación canónica es [math]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/math][/i][br][br]- Activar [b]ecuación general[/b]. Para la elipse del ejemplo anterior, la ecuación es [math]4x^2+9y^2-16x+18y-11=0[/math]. Se observa que [b]A[/b] de [math]x^2[/math] y [b]B[/b] de [math]y^2[/math] son positivos.

[b]Applet 2. Elipse con eje focal vertical[br][br][/b]Es un applet con las mismas características del anterior.[br][br]En este caso, el eje mayor es vertical y el eje menor es horizontal.

Vale la pena destacar que la ecuación canónica de una elipse determina el sentido del eje mayor dado que los denominadores son [b]a[/b] y [b]b[/b]. Además, siempre se cumple que [b]a > b[/b]:[br][br]- Si el denominador mayor es el denominador de [b]x[/b], el eje focal es horizontal.[br][br]- Si el denominador mayor es el denominador de [b]y[/b], el eje focal es vertical.[br][br][i]Si [b]a = b[/b], la elipse se convierte en circunferencia porque los dos focos coinciden con el centro.[/i]

[b]Applet 3. Otro procedimiento de construcción de la elipse[br][/b][br]En el applet se muestra un procedimiento geométrico para dibujar una elipse con el eje focal horizontal.[br][br]Active el proceso de construcción. Active el rastro y desplace el dial del deslizador. El punto [b]P[/b] deja su huella . La huella es una elipse con eje horizontal y se puede confrontar cuando se activa Gráfica.