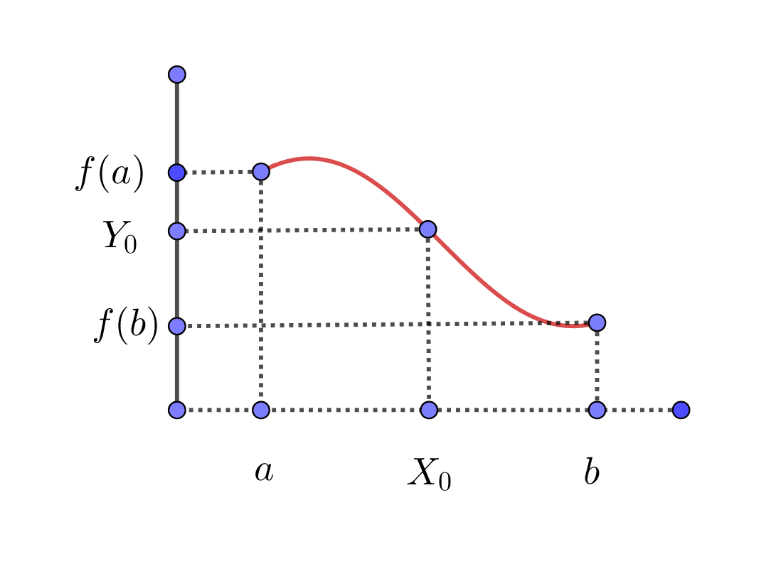
[b]Teorema do valor intermediário. [/b]Seja [math]f[/math] uma função contínua no intervalo [a,b]. Se existir [math]y_0[/math] , tal que[math]f(a)\le y_0\le f\left(b\right)[/math] , ou [math]f\left(b\right)\le y_0\le f\left(a\right)[/math] , então existe [math]x_0[/math] tal que [math]f\left(x_0\right)=y_0[/math].[br]Observações importantes:[br]A função precisa ser necessariamente contínua no intervalo [a,b];[br]Não importa se f(a) é maior ou menor que f(b), o teorema vale quando [math]y_0[/math] está entre f(a) e f(b);[br]Se f(a)=f(b), a única opção é [math]y_0[/math] =f(a), bastando tomar, por exemplo, [math]x_0=a[/math] para que o teorema seja válido.

Escolha uma equação movendo os controles deslizantes da construção e prove que a função [math]f[/math] possui pelo menos uma raiz real ou mais.