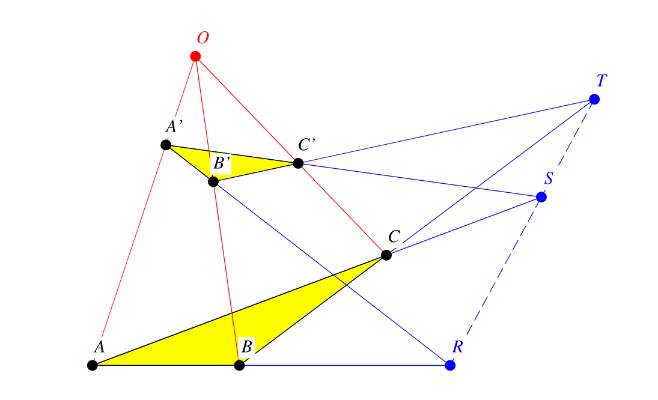
Desargues's Theorem

What does Desargues's Theorem state?
Let [math]\bigtriangleup ABC[/math] and [math]\bigtriangleup DEF[/math] be triangles lying in the same or different planes. [br]Then, the lines [math]AD[/math], [math]BE[/math], and [math]CF[/math] intersect at a point [math]O[/math] if and only if:[br][br] [math]AB[/math] intersects [math]DE[/math] at a point [math]L[/math][br] [math]BC[/math] intersects [math]EF[/math] at a point [math]M[/math][br] [math]CA[/math] intersects [math]FD[/math] at a point [math]N[/math][br][br]with [math]L,M,N[/math] collinear.[br][br]In other words, two triangles are perspective from a point if and only if they are perspective from a line (concurrency and collinearity).
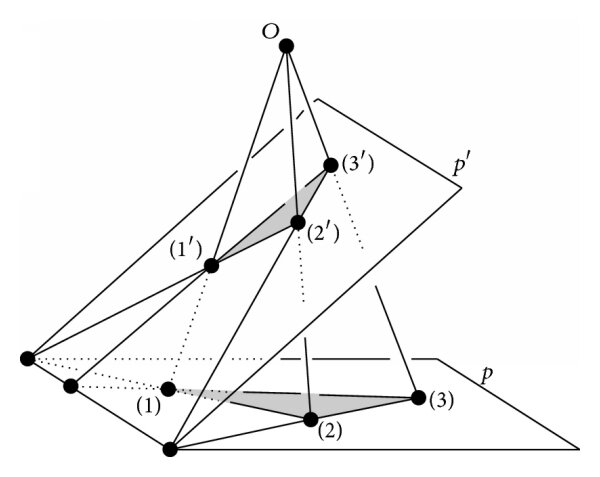
Proof for Desargues's Theorem
[b][br][br][br]Concurrency -> Collinearity (Non-Coplanar)[br][/b][br]Let [math]\bigtriangleup ABC[/math] and [math]\bigtriangleup DEF[/math] be two triangles that do not lie in the same plane. Assume the lines [math]AD,BE,CF[/math] all meet at a single point [math]O[/math].[br][br]Consider that each triangle defines a plane, can these planes [math]p1[/math] and [math]p2[/math] respectively. Since the two planes are not identical by assumption, they must intersect at a line. Call it [math]L[/math]. [br][br]Now, since the lines [math]AD,BE[/math] both pass through [math]O[/math], all these points exist in the same plane. In other words, we can say [math]A,D,B,E,O[/math] all lie in the same plane. Since this plane cannot be parallel to [math]L[/math], it will intersect [math]L[/math] at a unique point. This unique point will be the intersection of lines [math]AB[/math] and [math]DE[/math].[br][br]Repeat this logic for the planes containing [math]BE,CF[/math] and [math]CF,AD[/math]. We find that the intersections: [br][math]AB\cap DE[/math], [math]BC\cap EF[/math], and [math]CA\cap FD[/math] all lie along line [math]L[/math]. [br][br]Thus, concurrency implies collinearity for the non-coplanar case.[br][br][br][br][b]Concurrency -> Collinearity (Coplanar)[br][br][/b]Let [math]\bigtriangleup ABC[/math] and [math]\bigtriangleup DEF[/math] be two triangles that lie in the same plane. Assume the lines [math]AD,BE,CF[/math] all meet at a single point [math]O[/math].[br][br]We can use a method called lifting to perform a very simple proof. Choose a point [math]E[/math] that does not lie in the plane of the two triangles. Then, "lift" one of the vertices out of the plane by choosing a point, say [math]A[/math], and choosing a new point [math]A'[/math] along the line [math]AE[/math]. Similarly choose a new point [math]D'[/math] along the line [math]DE[/math]. [br][br]Now, we have two new triangles, [math]\bigtriangleup A'BC[/math] and [math]\bigtriangleup D'EF[/math] which are non-coplanar. Apply the above non-coplanar proof to these two new triangles, resulting in our line [math]L[/math]. Finally, project the configuration from point [math]E[/math] back onto the original plane. [br][br]Since projection preserves collinearity, we have that concurrency implies collinearity for the coplanar case as well.[br][br][br][br][b]Collinearity -> Concurrency (Coplanar/Non-Coplanar)[br][br][/b]The other direction is fairly straightforward. Assume [math]AB\cap DE[/math], [math]BC\cap EF[/math], and [math]CA\cap FD[/math] all lie along line [math]L[/math] with [math]\bigtriangleup ABC[/math] and [math]\bigtriangleup DEF[/math] non-coplanar. Then we must have that each of these pairs share a plane (the plane containing [math]A,B,D,E[/math], for example). These three planes will then intersect at a point, call it [math]O[/math]. (We're essentially creating a triangular pyramid using three planes, with point [math]O[/math] as the tip). [br][br]For the coplanar case, we can again use lifting in the same way do the for the forward direction, lifting up, applying the non-coplanar proof, then projecting back down.[br][br][br][br][b]Conclusion:[br][br][/b]From the above, concurrency implies collinearity and vice versa. Therefore, two triangles are perspective from a point if and only if they are perspective from a line.
Where Does the Theorem Fail?
In 3-dimensional space, Desargues's Theorem will always work. You can always rearrange the triangles in 3D so that the theorem holds. This assumption is a big part of our "lifting" proof above. [br][br]In 2D, Desargues's Theorem still holds for most planes. These kind of planes are called Desarguesian. However, Non-Desarguesian planes have been discovered in which the theorem fails. Examples include:[br][br]- The Moulton plane, which is identical to [math]\mathbb{R}^2[/math] aside from the fact that lines with a negative slope have their slope doubled when they pass the y-axis. [br][br]- Hall plane and Hughes plane: projective planes of order 9 which cannot be described using ordinary field arithmetic. [br][br][br]
Why Does it Matter?
In normal Desarguesian planes, the fact that Desargues's theorem holds is very deeply connected to being able to assign coordinates to all points and lines in a way that follows usual algebra. Because of this, Non-Desarguesian planes give us insight into alternative geometric systems and are therefore a huge subject of study in finite geometry, which has applications in coding theory, cryptography, network design, and quantum information theory.
