Durante tutta la trattazione fatta sinora, le coniche che abbiamo creato avevano a volte delle limitazioni. Arrivati al termine del percorso dovreste essere in grado di creare i seguenti tipi di coniche:[br][list][*][b]parabole [/b]con qualsiasi vertice, fuoco e direttrice;[/*][*][b]circonferenze [/b]con qualsiasi centro e raggio;[/*][*][b]ellissi [/b]con assi di qualsiasi lunghezza (verticale e orizzontale) ma [u]sempre con centro nell'origine[/u];[/*][*][b]iperboli [/b]con assi di qualsiasi lunghezza (verticale e orizzontale) ma [u]sempre con[/u][u] centro nell'origine[/u].[br][/*][/list][br]Per disegnare ellissi e iperboli con centro non nell'origine degli assi cartesiani ricorriamo al seguente teorema:[br][br][b][color=#ff0000][u]Teorema[/u][/color][/b]: [color=#0000ff]il grafico di una qualsiasi equazione nel piano cartesiano può essere traslato di un vettore [/color][math]V\left(v_x;v_y\right)[/math][color=#0000ff] sostituendo la variabile "[/color][math]x[/math][color=#0000ff]" con "[/color][math]x-v_x[/math][color=#0000ff]" e la variabile "[/color][math]y[/math][color=#0000ff]" con "[/color][math]y-v_y[/math][color=#0000ff]".[/color]

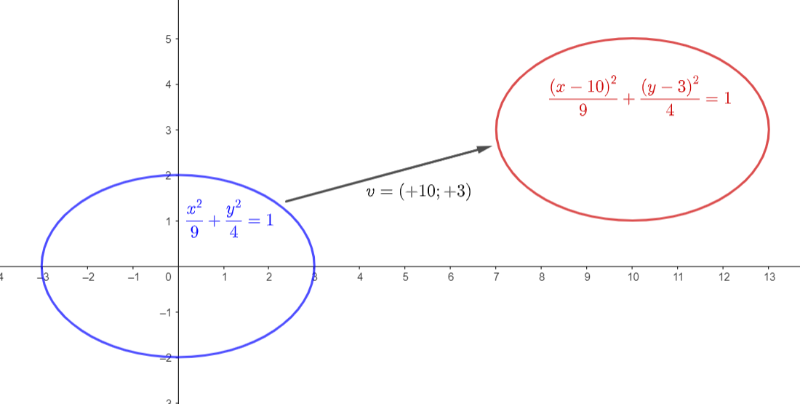
[b][color=#0000ff][size=150]ESEMPIO 1[/size][/color][/b][br]L'ellisse di equazione [math]\frac{x^2}{9}+\frac{y^2}{4}=1[/math] ha centro nell'origine degli assi ma può essere facilmente traslata in modo da avere centro nel punto [math]\left(10;3\right)[/math] tramite la trasformazione delle variabili descritta nel teorema, quindi sostituendo nell'equazione "x-10" ad ogni "x" e "y-3" ad ogni "y". [br]La nuova ellisse ha quindi equazione [math]\frac{\left(x-10\right)^2}{9}\frac{\left(y-3\right)^2}{4}=1[/math] e mantiene tutte le proprietà dell'ellisse di partenza (lunghezze degli assi, distanza focale, eccentricità).

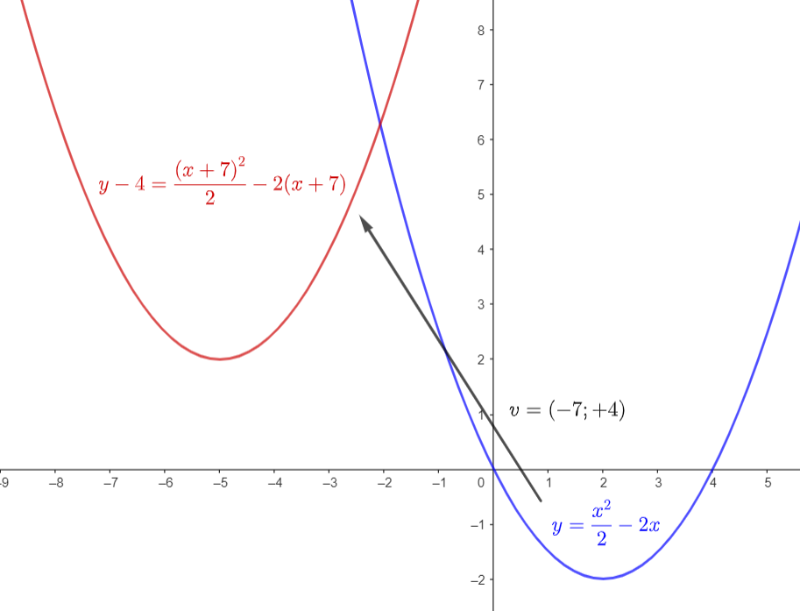
[b][color=#0000ff][size=150]ESEMPIO 2[/size][/color][/b][br]La parabola di equazione [math]y=\frac{x^2}{2}-2x[/math] ha centro nell'origine degli assi ma può essere facilmente traslata in modo da avere centro nel punto [math]\left(-7;4\right)[/math] tramite la trasformazione delle variabili descritta nel teorema quindi sostituendo nell'equazione "x+7" ad ogni "x" e "y-4" ad ogni "y". [br]La nuova parabola ha quindi equazione [math]y-4=\frac{\left(x+7\right)^2}{2}-2\left(x+7\right)[/math] e mantiene tutte le proprietà della parabola di partenza (ampiezza rispetto all'asse di simmetria, distanza fuoco-direttrice, eccentricità).

[b][color=#0000ff]ADESSO PROVA TU[/color][/b][br]Scrivi l'equazione di una conica qualsiasi e usa il file già pronto qui sotto per traslarla di un vettore a scelta. Sfida il tuo compagno di banco a scrivere la giusta equazione per la conica traslata!