기울기
[b]지금까지 일차함수의 그래프에 대해 계속 알아보고 있습니다.[br]일차함수의 그래프는 어떤 모양이었죠? 네, 맞아요. "직선"입니다.[/b][br][br]그렇다면 <직선의 특징>을 한번 살펴볼까요.[br][br][u][color=#9900ff]다음 직선과 직선이 아닌 두 도형이 있습니다. [/color][/u][br]1. 어떤게 직선인가요? [br]2. 직선이 아닌 것과 직선인 도형은 어떤 차이가 있나요?
그렇다면 이 두 도형의 차이를 수치화하려면 어떻게 나타내야할까요?[br][br]자, 다음 두 직선 f, g가 있습니다. 이제 이 두 직선을 기울어진 정도로 구분해볼게요.[br]어떤 직선이 더 가파른가요?[br]
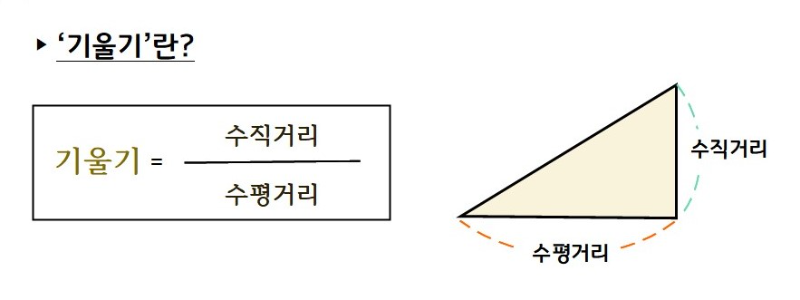
일반적으로 기울어진 정도, 즉 "기울기"는 다음과 같이 '수'로 나타내요.[br]

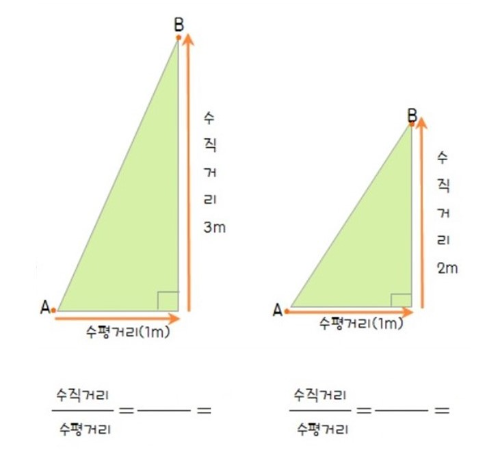
자, 그러면 이제 좌표평면 위의 선분의 기울기를 구해볼까요?
감이 좀 오셨나요? 그럼 처음 봤던 두 직선으로 돌아가볼게요.
정리해봅시다.[br][br]좌표평면 위의 직선의 기울기란?
교과서 104쪽 문제 2번
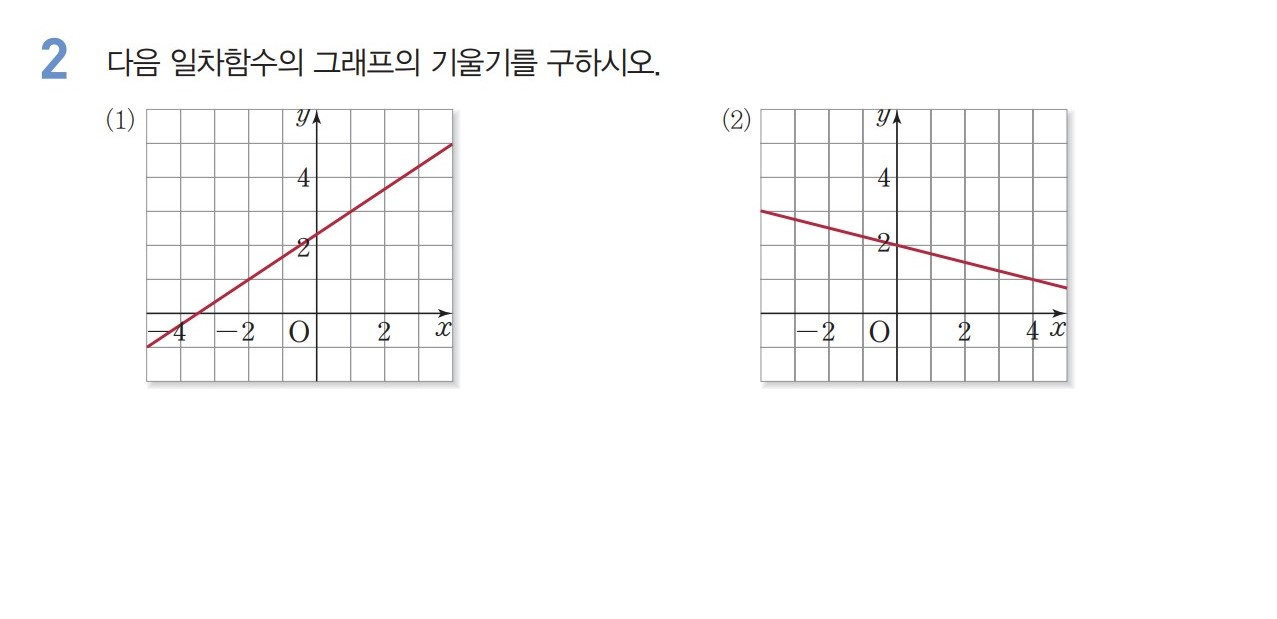
[b]자, 여기까지가 "그래프"에서 <일차함수의 그래프의 기울기>를 구하는 방법이었어요.[/b][br][br]그렇다면, [color=#0000ff][b]"식"이 주어졌을 때는 기울기를 어떻게 구할까요?[/b][/color]
교과서 104쪽 문제 1번

다 왔습니다. 그럼 제대로 공부했는지 점검해볼까요?
[b]1. y=2x+1에서 기울기는?[/b]
[b]2. 두 직선의 기울기가 각각 2와 5일 때, 어떤 직선이 더 가파른가요?[/b]
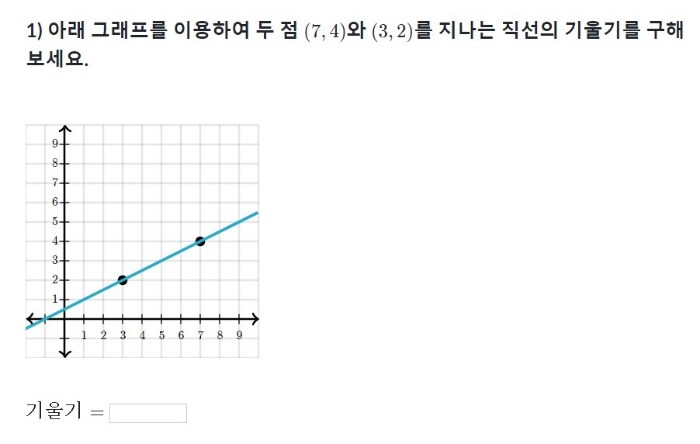
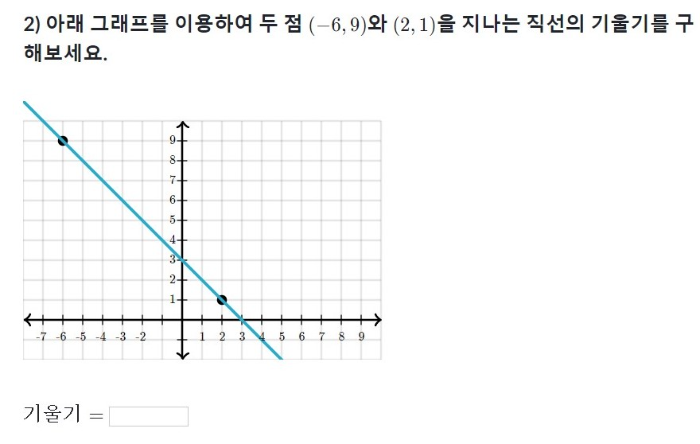
3. 두 점을 지나는 직선의 기울기를 구해봅시다.