
Mengenal Persamaan Garis Lurus

Sistem Koordinat
Sebelum mengenal persamaan garis lurus, sebaiknya kita ingat kembali materi tentang sistem koordinat dan fungsi. jika berkaitan dengan fungsi maka akan kita ingat sebuah variabel-variabel dan bagaimana cara menentukan nilai - nilai variabel. Dalam sistem koordinat nilai koordinatnya ditulis dengan bentuk (x,y). untuk itu dapat kita lihat tabel berikut menunjukkan nilai masing-masing variabel untuk persamaan 4x − y = 5.
Tabel nilai variabel persamaan
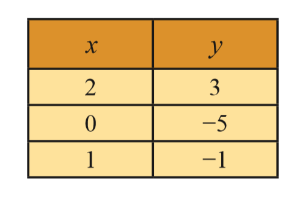
Berdasarkan tabel diatas setiap pasangan berurutan (2, 3), (0, −5), dan (1,−1) merupakan penyelesaian dari persamaan 4x − y = 5. [br]yang menjadi pertanyaan berapa banyak penyelesaian yang memenuhi 4x − y = 5? [br]Sesuai dengan konsep sitem koordinat yang tidak memiliki batas maka penyelesaian yang tak terhingga.
Tambahan
Lengkapilah tabel berikut yang memiliki persamaan 2x + y = 5
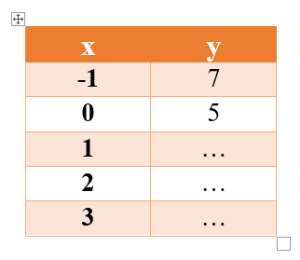
Tabel persamaan 2x + y = 5
Penyelesaian
Untuk yang pertama berdasarkan nilai diatas untuk nilai x = 1[br]2x + y = 5[br]2(1) + y = 5[br]y = 5 -2[br]y = 3[br]maka menghasilkan nilai variabel yaitu (1,3)[br][br]yang selanjutnya untuk nilai x = 2[br]2x + y = 5[br]2(2) + y = 5[br]y = 5 - 4 = 1[br]maka berdasar diatas nilai koordinatnya adalah (2,1)[br][br]dan yang terahir x = 3[br]2x + y = 5[br]2(3) + y = 5[br]6 + y = 5[br]y = 5 - 6[br]y= -1[br]maka berdasarkan diatas nilai koordinat xy nya adalah (3,-1)[br][br]Berdarkan data diatas maka di dapatkan nilai - nilai dari tabel.[br]
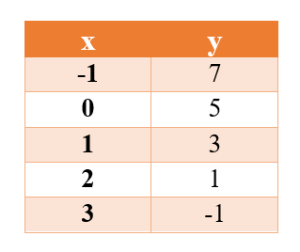
Tabel persamaan 2x + y = 5
titik koordinat berdasarkan persamaan
berdasarkan nilai dari tabel diatas maka kita dapat mengetahui letak titik berdasarkan nilai diatas.[br]berikut titik koordinat hasil dari pasangan berurutan (x,y) yaitu (-1,7), (0,5), (1,3), (2,1) dan (3,-1)[br]kita buat pada seistem koordinat sehingga membentuk berikut
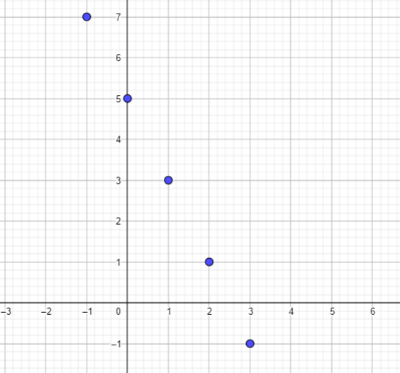
titik koordinat dari persamaan 2x + y = 5
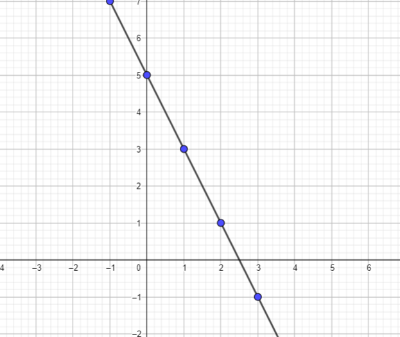
dengan menghubungkan titik-titik maka kita dapat membuat sebuah garis lurus.
sebagai tambahan buatlah gambar persamaan garis x - 3y =7
Hint *[br]1. Untuk menyelesaiakan permasalahan diatas pertama buatlah titik - titik koordinat dengan tool berikut
2. hubungkan titik dengan klik line dan klik pada titik - titik
kesimpulan
Pengertian dari persamaan garis lurus ialah sebuah persamaan yang jika kita gambarkan ke dalam sebuah bidang koordinat Cartesius yang nantinya akan membentuk sebuah garis lurus.[br][br]Serta yang di maksud dari garis lurus yakni sekumpulan titik – titik yang letaknya lurus atau sejajar.