IM Geo.3.12 Lesson: Practice With Proportional Relationships
These are the plans for a vegetable garden that a school is designing.
[size=150]Scale: 1 unit = 2.8 ft[/size][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYUAAAEsCAYAAAAsMK9uAAAgAElEQVR4AeydBXRURxfHJ+4hbsSVeLAEJyGCu7u7u1NIQgIE70dpCy3aAoVSpFCkUNyLFK97ixYotEjh/507L5ssyW6yu9kku8m8c3Le7pO5c3+zuXf0DoM4BAFBQBAQBASBbAJMkBAEBAFBQBAQBGQEhFOQkRBnQUAQEAQEAQinIH4EgoAgIAgIAjkEhFPIQSE+CAKCgCAgCAinIH4DgoAgIAgIAjkEhFPIQSE+CAKCgCAgCGjFKcyZMwcpKSmoU6cOmjZtiosXLwqygoAgIAgIAnpIoEhO4ffff4ePjw+io6OxcuVK7Nu3D0OHDsVPP/2khyhElgUBQUAQEASK5BT8/PzQokULQVEQEAQEAUGgjBDQ2CkcOHAAZmZmePDgQRlBIdQQBAQBQUAQ0NgpJCcno3fv3oKgICAICAKCQBkioLFT8Pb2xooVK8oQCqGKICAICAKCgEZO4eHDh3BwcMCOHTsEQUFAEBAEBIEyREAjp0D6u7m5Ydq0aWUIhVBFEBAEBAFBQGOnsHnzZjDGsH37dty6dQu//vorTpw4gRcvXgiqgoAgIAgIAnpKQGOnQPqOGzeOOwZyDvTXpk0bPHv2TE9RiGwLAoKAICAIFMkpCHyCgCAgCAgCZYuAcAplqzyFNoKAICAIFIlAsTuFV69e8XGHjIwMXLt2rUiZFS8LAoKAICAIFC+BYncKkyZNyhl3MDIywsmTJ4tXI5G6ICAICAKCgMYEitUp0KwkZ2fnHKdAg9E9evTQOLPiRUFAEBAEBIHiJVCsTuH+/fvw9PR8zSn069eveDUSqQsCgoAgIAhoTKBYnQLlatOmTTxwHrUSHB0d+ee0tDSNMyxeFAQEAUFAECg+AsXuFCjrR48e5a2Fv//+m4fGIAfRunVrUEtCHIKAICAICAK6Q6BEnMJ3333HncLTp0+55hRuOyIiAvb29jh79qzu0BA5EQQEAUGgnBMoEadw8+ZN7hSePHnyGu4RI0bw6/Pnz3/tuvgiCAgCgoAgUDoEStUpkMoUaZWmqlKIjEePHpUOBSFVEBAEBAFBgBModadAubh37x5ofwZLS0vcuHFDFI0gIAgIAoJAKRHQCacg010WYG/evHmyS+IsCAgCgoAgUIIEdMopkN4bNmzg4wwdOnQQs5NK8IcgRAkCgoAgQAR0zilQpmhsgTbxod3dvv32W1FSgoAgIAgIAiVEQCedgkx32eykxYsXyy6JsyAgCAgCgkAxEtBpp0B6b9y4kXcndevWrRgxiKQFAUFAEBAEiIDOOwXK5OPHj1GxYkWYm5vjypUrouQEAUFAEBAEiomAXjgF0v3ly5cYPHgwbzW88847xYRDJCsICAKCQPkmoDdOQVZMH330EXcMLVu2xPPnz2WXxVkQEAQEAUFACwT0zimQzr/88guCg4N5WO6LFy9qAYNIQhAQBAQBQYAI6KVTkBVdz549eath1apVskviLAgIAoKAIFAEAnrtFEjvrVu3csfQtm1bPu5QBBbiVUFAEBAEyj0BvXcKVIK0wM3Hxwfu7u4idlK5/0kLAIKAIFAUAmXCKcgA9O7dm7caVq9eLbskzoKAICAICAJqEChTToH0pu0/aWc3mp0kDkFAEBAEBAH1CJQ5p0Dq005vYWFh8PPzw+nTp9UjIp4WBAQBQaAcEyiTTkFWnk2aNOGthu3bt8suibMgIAgIAoJAAQTKtFMgvT/99FPuGNq1awfZHtEF8BC3BAFBQBAo1wTKvFOg0v3yyy9hb2/Pu5N+//33cl3gQnlBQBAQBAoiUC6cggxA9+7dxewkGQxxFgQEAUFAAYFy5RRI/xUrVnDH0KNHDwU4xCVBQBAQBMo3gXLnFKi4f/75Z/j7+/MFb5cuXSrfvwChvSAgCAgCcgTKpVMg/V+9eoVmzZrxVsOWLVvkkIiPgoAgIAiUXwLl1inIilwWipt2dnv48KHssjgLAoKAIFAuCZR7p0Cl/tVXX8HKygoeHh64d+9eufwhCKUFAUFAECACwinI/Q569erFu5NWrlwpd1V8FAQEAUGg/BAos07hzp27OH/hEl7891Kt0ly8eDF3DP3791frPfGwICAICAJlgUCZcgqXL19G1x5SbZ+C4lmaMG7g7Z1csXjJm/jvv/9UKjMKxe3m5oaAgAD8+OOPKr0jHhIEBAFBoCwQKDNOYdXqNdwBBNgzjG8RiKW9o7F1XE281TcGfeK9+L2wqCp8OqoqBffy5Ut06tSJv0drG8QhCAgCgkB5IFAmnMKIUaO48R6a4ovj6Q1wJjORn4+kJvDzqYxEnJydiBgvcxgYm+GPP/5UuWwXLVrE0x4/fjz++ecfld8TDwoCgoAgoI8E9N4pjJswiRvtN/tE42JWMg7NiscXM/P/Hc12EFW8zOEbEIz/Xqo+1kBdSDQ7ibqU/vjjD30sZ5FnQUAQEARUIqDXTmHs+AncISzvVwUnMxoodAbyDoIcA/2ZMoYevfqqBEj20P3799GmTRtYWlqC1jaIQxAQBASBskhAb53C6LHjuEOgMYNzc5IKdQgy53BidgOsHRbL3133wQdql2lWVhZ/d+DAgWq/K14QBAQBQUDXCeilU5g8dSo3zNRldHJ24S0EmUOQnWmMYVhDXz6+8PXX36hdRufPn+fdSVWqVBHdSWrTEy8IAoKALhPQO6cwbIQ0qPxO/8o4N1f1FoLMIdD50Mx4XFqQguo+5qgaV1vj8qHuJJr6um7dOo3TEC8KAoKAIKBLBPTKKbwxaxY3wot6ReFkRmK+LqPDsySDL3MANPtI9jnv+WhaAj4eV5Ond+bsOY3LJDU1lacxbdo0jdMQLwoCgoAgoCsE9MYpDB46jBvf9wZVVTiGQLX/9SNi8dmUuiDn8PmMelg1pDoKcgzUjdQ40h7Va2reWqCC/P777+Hk5ARfX1/cvHlTV8pW5EMQEAQEAbUJ6IVTSM/I5A5hQfdIkCHPW+un78fSEjC1TShmd47AVwtSML9HNCa0rMTXKSh6nq5RWhNbBsHSylptcHlfuHPnDuLi4mBsbIyjR4/mvS2+CwKCgCCgFwR03in0HziQO4S1w6orbCHIDD61FA68UR+DUwLQta4PP5/JLHjMgRa6vdU/BpbmZqBYSdo43n33XZ5f2vpTHIKAICAI6BsBnXYKGXPmcgOb1T1KaQtB5hToTAvXqMWwe0pdfpa/p+gzOYX/9SWnYI579+9rrewOHDjAWwy1a9cGrW8QhyAgCAgC+kJAZ51CvwGDuENYN6w6zqqxDkHmHBQ5gbzXTqQ3wMIekTA3M8Oz58+1XmYNGzbkOnz88cdaT1skKAgIAoJAcRDQSaeQOXdedgshkscxymvMtfWdnE2/eC+4engXB1ueZkZGBteFYieJQxAQBAQBXSegc05h0JCh3IjSGMLpTMWDytpwCtTVdHhmPFzMGdIz5hZrOV29epXHTYqJicH169eLVZZIXBAQBASBohDQKafw4YZNOS0EZV1GNN2UppnSuSjOgdLP7BTK5akTNVVT2E+ePEHlypW5vLNnz2qajHhPEBAEBIFiJaAzTuHs2XPcYE5vE6J0DIEcAS04WzMsFlvG1uQDyzTrSF3nQKExtoytweXNmZtVrIDzJk57M9AqaBE7KS8Z8V0QEAR0gYDOOIUWrdshzNUI1xc3UmrkaRXygp5RGN0sGIMb+mNa2zClobKVOYov5yZh1ZBq3DC3bN2uVMpg165dMDExQf369XH79u1SyYMQKggIAoKAIgI64xSo9ky7pdGMIGUGna6TY6BIp3QelOyPFQOr8nDYBb1D96iVQYvV0jtKXUYdOnVVxKNEr9WtWxfm5ubYvXt3icoVwgQBQUAQUEZAp5zC2mFxKq0vICNP6xHeHVQNM9qGFbhqWeZIaNC6bXUX3kJY+uYyZTxK/LosdtLkyZNLXLYQKAgIAoJAXgI65RRWD41V2SkcT09AeqcI0MI2chDKWgo0frB7Sh1U9baEsbkV9uzdl5dBqX8/ceIEbG1tkZCQgN9++63U8yMyIAgIAuWXgM44BSNTK4xvHqDyugSagbR6aHV8NrUuD4WtyClQ62DjqDgYMwbfwFDcvaudUBbF8XP5999/ERsrbf5DK6LFIQgIAoJAaRDQGacwddoM3rVDA8EF1fzljT85BkWzj2j8gNKZ2a4ST7NN+4548eJFafBVW2Z6ejrP86xZs9R+V7wgCAgCgkBRCeiMU3j27Bmq16gDFwuG7RNq82mptMBM3gmo8pniGR1PS0Cv+p7cuM5MTS8qoxJ///Dhwzzv1HL466+/Sly+ECgICALll4DOOAUqAqrNe3h6c4M4tVUgTs1uwGcM0UyjghwCtQzIGdBObJ+MrwUfO0OexqnTp/W2ZCmQXs2aNWFvb4+DBw/qrR4i44KAIKBfBHTKKcjQrVq9FkYWFbhhH9vMHxtH1+Ath3NzkviezDR4TH80ZnB+XjJ2Ta6D94dUQ91g6Z3GzVriwYOHsuT0+jw1ez/qN954Q6/1EJkXBAQB/SCgk06B0N26dQtZ8xeCManWH+pijNZVnDC5hT+mtw7EjNZBGJrshTBXE1gyxh2Ii4c3duzYqR/k1cglbdpD6zgSExPx8uVLNd4UjwoCgoAgoB4BnXUK8mp89/2P6NG7H2rVa4CQiMrwDQrjf+Ex1dGhc1fQuoOnz7Qf+lo+D6X9+b///gPtz0DOQSx2K+3SEPIFgbJLQC+cQl78NChNf+XxGDduHHcMy5cvL4/qC50FAUGgmAnopVMoZiY6n/ylS5e4YwgLC8PTp091Pr8ig4KAIKA/BIRT0J+yei2nv/zyC2rVqgVnZ2fQFFZxCAKCgCCgDQLCKWiDYimmMWrUKN5qyMzMLMVcCNGCgCBQVggIp1AGSvLQoUPcMdCe0I8ePSoDGgkVBAFBoLQICKdQWuS1LJfiOlWvXh3W1tY4cuSIllMXyQkCgkB5ISCcQhkr6dGjR/NWw5IlS8qYZkIdQUAQKAkCwimUBOUSlkFRVg0MDBAfH4/Hjx+XsHQhThAQBPSZgHAK+lx6BeSd9mWoUqUKXFxccFqPY0AVoKK4JQgIAsVAoMw5hW+++Ra9+w5AbM26qOjtizrxiVj5/mo8fvykGPBpnuTz58+xYNEStGrbAU4u7giNiMLQEaNx5uw5zRNV8KaYnaQAirgkCAgCSgmUGadAsZKqVK/B+9ODnAyRUKkChiR7o2UVR9gZSbGRsubPVwqiJG/MmTOXx3SyZgw1/CzRq15F9KzrgcqeJjz/pMfX33yjtSzt2rULpqamaNWqFW7fvq21dEVCgoAgUPYIlAmn8NXly3B0cUcFE4YVg6qAQmmfyUzMiaK6b3o9zO8ewQ1utx69SrUUR4waw/PRo64n9k+vz6O9nslM4lFgKfz3zom1UcPfij9z+vQZreWVnGZgYCDf9vPq1ataS1ckJAgIAmWLgN47hQsXLnIDSi2DS/NTcCK9AfJuziNzErsmSwHlhgwbXiqlWL9BMs/r5jE1cCErmTsv+X0iaBc52juCwoF3runKn/3jzz+1mtdJkybxdLOysrSarkhMEBAEygYBvXYKN7/+GqZWdqgXbMu38CTjL29k836mmvjb/Spzo7ht+44SLcEevfpwubTvA+0DkTdv8t9Jj1MZDVDZyxzVatbVej4/+ugjnpe2bduCoq+KQxAQBAQBGQG9dQrnzp3jhi0p3A6XFzbMV+uWN7Lyn6mGPrKxH3/3++9/kHEo1nNCotRC2DO1Lt9JTj4/yj4fTU3gOlGo7F59+ms9f0+ePEFwcDAfa7h586bW0xcJCgKCgH4S0Eun8OOPP8HY0hY1A2x4d1FhLQR5w0tdS9TFFOZmitCIysVeaj379JNaCIOrqewQZPk9MbsB5veI5O9/cah4gt6NHDmSp79w4cJiZyEECAKCgO4T0DunQHPuqfbcKNIBV9RoIcgMLZ2PpCbgRHoCTBnD0OEji62U4hNTeF73TFO9hSCfT/p8MSsZwxv6gjEj/Pjjj8WS1x07dvB8tmnTBn/99VexyBCJCgKCgH4Q0Cun8MMPP8DIzBq1qIUwu0G+LiNqMdBgrcywFtSCOJWRiLldw7kxvH9f+4awa49ePO1VQxS3EOTzJv9ZlnfZmVo2tB+1qwVD3wGDi+1Xdf/+fbi7u/PYSd9ocTpssWVYJCwICALFQkBvnMKpU9RCMESjKAdcmKd45s7H42qB+u3JkH4+oz4+GlMzn+PIMbYz40EDz+Guhhg8TLuthZTGzbhD2DGhNk5m5B9U3jutHraOr8XzSQ5hy9ia2DetXo4zk+VRdiansLBnFE+zWH4FcomOHTuWy3nzzTflroqPgoAgUF4I6IVT+P6HH8CMzVEz0IbXmhXVrI+lJWB44wCsGlqdT+ncMKoGBiQF8OdlxjXvmWYBDWjgDXsnV62Vd8cu3blRXT20usIxBMr7hyNrYFCyP87OSeTdQx1renLHoEgvyjNdJ6dhbczwybbinzX14Ycfch3at2+Ply9fao2NSEgQEAR0n4DOO4XTZ85wh0BjCOfmJCqt+dM4wYZRceiT4IuJrSqhVXUPbJ9YW+nzZGyppbCsXwwszMxwXwt96c1atoYBY9zAU+0+rxOSfT+SGo+RTYMwqVUljGoahINv1M+3tkL2rOxMYwu+9oaYMGlqifyqaOVzUFAQHB0dcf369RKRKYQIAoJA6RPQaadAs4wYM0atAGuczUwq0MCT8aTWwrYJtbG4VwzvnqHvMqOq6ExO4X99o2FpYY57RRxXaNexM69drx0Wi9MKuozk5dO4Bzmx5f2r8D/5cRD55+Q/fzk3CXWDrEEtkZI8hgwZIrqTShK4kCUIlDIBnXUKtA7ByNwaDSPs+UIuZV0r8oaTPtNztCpYlefJKbzZJxqW5uZ48PChxkXRpn1H3kLYOCquwO6qvHmltQj0l/e6ou+0vsLTlmFmarrG+dT0xQ0bNnDH0KFDB02TEO8JAoKAnhDQSafw888/cyNUM8AaX84rvIWgyIiqco1mIE1sEQQLK2uNi6t12w48rx+MKLyFoEqeFD1DA+fH0uLhYM7w9rsrNc5rUV789ddfERYWBldXV5w5o72YTEXJk3hXEBAEtE9A55wCxTKi0BW0Uvl4umo1fkWGVJVr5BTiQ2zQsElzjch26tqNtxDWDY9Vq4WgSt7kn6EWzVv9pfAct+/c1Siv2niJQmJ07y4NpNNgtDgEAUGg7BHQKadw9949XuuO9bfGVwtSlHYBqdIHL29UFX2m8YZNo6VQ26c0iEYqi2W0cXRcoWMIiuSrc+3snCQ0irBHaGSMTvwCt27dysupRYsWePHihU7kSWRCEBAEtENAZ5zCv//+i5CwKNQJtMKxtPwL02RGlMYK9k+vxxepqdofL3tXdqY0aDZPkIsx6sYnqk3y3RUruVF8q1+MwmmnMjkH3qjP10tQPqkLSHZdnTMNWi/vF8PlHThwUO28FtcL165dg6+vL/z8/ECLCsUhCAgCZYOAzjiF8RMn8a4YmrtPM3MUGU6KWTS6WRCGNgzAiCaBWDs8FodT1TO2ZKCPpScgObwCTMytcffuPbVKkra5ZIbmmNoqiK+HUJRPasnQHg79E/0xtGEgprcLk6adyq22VvRe3mu0J8Tb/atwhzA7c45a+Syph3v1klZuv//++yUlUsgRBASBYiSgM07B3NoeY5v6881x8hpH2Xeq4dOitM+m1MXG0TXQM96Xb0qjykwjSoOcCjmEUBcTVHBwws2bX6uN9v1Va7iRpjAbhdX+t46rhc+m1kVqx3BMbVOJy5fpUtCZ9KEpqBmdw7isvv0HqJ3Pknzhgw8+4Pls165dSYoVsgQBQaAYCOiMU6Agd+tHxPG1BoUZTDLGtDhsae/KSO0YxhehFfQO3Ts3NwkrBlaBMWOoVqMOHj58pBHOlm3aIyHEusBuI1leyLjTHzmjNrEVcTJD+YI22TvUSiLdmsU4ckO78j39qIHT7KTw8HB4eXnh1KlTGrEVLwkCgkDpE9App7BmaGyhTkFmPGmgmJzCzA4FOwVyIOQQFmSHoKY1BUXZWKZh0xZoHk1rJ/LHNJLlLe+ZWhUtqnsU+g49Rw4hzJX2ajbGnr17S/8XomYOUlKkyLB79TDvaqoqHhcEyiQBnXIKS3tHqdzFQsZ+VodwfDy2ltJZSlTrpvhGzWOcea179dp1RS7EaTNmwtOGFdjNJe8UqKVAgflmti/YeVF3Ea1wphZTdNU4PH36tMh5La0E9uzZw/Vo2bIlaAKBOAQBQUB/COiMU4irVRdRHia4saTRa+Gv5Q1s3s/UWiCjm/c6fadaNw0q1wm04QZq1+7dWimV4ydO8PR2TqzFZSiSnfca5VHZNFpybjQTal52GO9mLVoVqSWjFSW1kAgtcLOxsUFgYCAePHighRRFEoKAIFASBHTGKXz33XdgzACjGvvx2r0yY5/X4Cr6TtM4N4yM48bbyc1T6xx79x0AM8awtwib51C+yamR82peWWrJvL96jdbzWtoJ9uzZk5fDe++9V9pZEfIFAUFABQI64xQor9u3SzuA1Qu2xfm5STg3J0np9NS8zoBq3DSge21RQ0xqEcQNEYWg+O8/7Yd+pgVbderFcxmLe0biq/kpfCxAVUdG3Vrn5yVj24RaiKloxtPZ//nnKhSXfj6yYsUKriNNXxWHICAI6DYBnXIKhOrm198gpqpUy+9S0xV8o5rZDfggLXUHyRveI7Okmjb1x1Ote0mvGLhZMzBDUyx983/FTj5tdiYfEK5gwjC/WxQOzKgPWn1MeSHDL+syojNdo3UH9Ld9Qm10r1ORG8rImCrlYlUwxbOiriRa8Hb58uViLxshQBAQBDQjoHNOQabGuvUfwCdImqdfzcccM9oEY+PI6tg/rQ6uLkzBV1nJ2DW5FmZ3rISWVZwR5GjAjWxszTr4/vuSW2F75coV9Ok3gMt2NmPoWtMd7w+qjG3jauB0RgLP69nMBnh/UBX0S/BCvSBb/iztIvfOu+/K1C0XZ9qwhwafaTB906ZN5UJnoaQgoG8EdNYpyEAeP3EKbdt3gpOLG49mampmnm1UGYyMTWFr5wDfgBCMmzAZf/zxp+y1Ej+/fPUKi5a8Cb/AEFSwc4CZhWVOPskImltYwdHFnYfV+GzvPrx69arE86grAmmxm5GREfr06YO///5bV7Il8iEICAIAdN4pyErp2bNnuH79Bs59+SU2b/kYn2zbjpOnTuHPW7dkj+jM+Y8//sClry7js8/24OOPt+KzPXtw9eo1ncmfLmTk0qVLsLOzg7e3N+7cuaMLWRJ5EAQEAX1yCqK0yh4BWShuExMTrF27tuwpKDQSBPSQgN60FPSQrciyigQWLVrEu9oGDhyo4hviMUFAECguAsIpFBdZka5aBL755hs4OzsjNDQUf/5ZemNDamVaPCwIlEECwimUwULVV5Vo8L1jx4681bByZelsO6qv7ES+BQFtERBOQVskRTpaI7BgwQLuGKZNmwaaxioOQUAQKDkCwimUHGshSQ0CtNjNwsIC7u7uoNlc4hAEBIGSISCcQslwFlI0IHD37l2+2M3S0hK7du3SIAXxiiAgCKhLQDgFdYmJ50ucwMKFC8XspBKnLgSWVwLCKZTXktczvc+fPw8zMzNUr15drILWs7IT2dUvAsIp6Fd5lfvctm7dmrca1q9fX+5ZCACCQHEQEE6hOKiKNIuVwOzZs7ljmDlzZrHKEYkLAuWRgHAK5bHUy4DONDvJwcEBPj4++Pbbb8uARkIFQUA3CAinoBvlIHKhAYF79+6hfv36oNhJx48f1yAF8YogIAjkJSCcQl4i4rveEXj77bd5dxKF4i6ug0J8U7dVRkYG/6Ouqz179hSXOJGuIFBqBIRTKDX0QrA2CRw6dAhWVlaoU6cOaH2Dtg9aJ0H7YvTt2xddunRBmzZtsGrVKm2LEekJAqVOQDiFUi8CkQFtEkhKSuLG+9NPP9VmsqDZTuRwxCEIlHUCwimU9RIuh/rNmzePO4YJEyZoTXvqLho6dKjW0hMJCQK6SkA4BV0tGZGvIhGgxW5OTk6Ii4vD999/X6S06OXRo0fDw8MDTZs2RYMGDZCZmSmC9RWZqkhAFwkIp6CLpSLypBUCtIVrtWrVeKvh7NmzRUqTHMuaNWtw4sQJvPfee/D19UWjRo2KlKZ4WRDQRQI64xQePnwI+icuykEzRJ4+fao0Cdr+8dHDR0rvq3KD0njw4GGBjz569AjPnz0v8JnCbv796O8C03jx4j+QnKIcL168wMNCdHn48BHouaIcjx8/LrBsiSnpW5SDQmwr02XZsmXcMYwaNaooIvK9SwPP5CTEIQiUJQI64RQ2f7SZ/9PaWTlg+7bt+fg+ePAAo4aPRt3Y+lj5bv7NV8iZjBw2Skqjgj3u37+fL43nz58jJDiEP9OrWy/cvXsv3zNbNm9B0+Rm6NOjL3799dd8948ePQpvNx+exoIF8/PdpwsrV6zk951sXbDtk235niGn1a9XPyTWScZHmz7Kd582mhk8YAhPw8vTG7dv3873DF2grgwySv17DwA51LzH+nXrEV+rAYYOHAZa6JX3OHniJLxcvXkaS5YuzXubf1/x7gp+39vNF1s/3prvGXJK/fv0R70a8di4YUO++3ShZ9eePA1Pdy+FIbDJYQT4BfBn+vbsp1iXtevRKKExhg0arlCXz/cfgH/FQJ7G4sWLFeZj3759MDU15esa7ty5o/AZdS8S/y+++ELd18TzgoBOEyiyUyBjW1DtnLS/efMm/4d98uRJPhj0vq+nH/wG2yNkjBN/bsLY1wcIGyU2BrNncGljzu+vXb0uJ50nj5+gVrXaYMYM1d/yhYEvQ/qs2Tn3ZR+WLFwCZsZQc6UfmCODq70b7t/LdR779+7nads3MgXzZagWVR3//vOv7HWsfm81v+/V3Rbh011hbWGDX37+Jee+7IO9nQN8B1AFWmUAACAASURBVNgjYJgjfz5rzuvOo2FCIzA7BrdOVvz++rW5MXz+/vsxqkRUBTNniHvXD8yFYcyIsbKkc847tu4As2CIe8cPzInBy8Ubf97K3cKSjCQZLEfSxYchKjQGxFl2LCYWjKFiJxtEZbjD0dIZv//+u+x2ztnYyBgBgxzg18+ePz9h3MSce/QhoW4Drot7Z0mXVe+tzrl/+9ZtVA6vAmbDEPe2L5gbQ14W9PCypW/xNOLe8gNzZqhgYffa72n/PqlcnFqYg3kyBPuG5MigD+8sf5fnzb2dFSJnu8PFxg0FGf0aNWrA3NwcNIVV1YPY5d3TgVofLi4uBbaAVE1fPCcI6BIBjZ0C1bxCQkLg7e3N/zns7Oywf/9+hboV5BSo26CiiydqrvFDk8NRqDpPqr2OHTmOp/Xucqm2mrQzDE2PRyN0khs3Av88+YfPR3e0cYZxEEODT0L5fYcEEzRLaZ4vH5lpmTBwZWh6MhrJn4XDuroRLIysceb0Gf6sObOET087fr/RgQhudPv3GsDvpc1M4zIrjXFDk2NRqLM+AJamVrh8+cprcv66/xdsbGxRea4XmhyJQuU5UquiV7feUjqzpHQafh7B0wkdL+lCN3/88Ud4uniDeTAkfRrOdbGqboCh/Ye9JoO+EBuTSgxNT0QjeXc47OqbwJiZ4sb1G/xZZ2tX7pjofsP9EWDWDP169ef35s+TdjULn+TB89j4VDjMmRVu3JDelRfGTBjilvmi8dEoVM2SyoVaHnRkpmdyJin7wtHkaDQqjXbl3+keddFZGFnCyI8hZU8419UuwQT9e0o85WVkzZ4PqxqMP5O0Oxw2sUawN3PE+S/Pg7qVHMyc4NvPnpdL0qdhYFYME8dKzonO5NzCxkvl0mBnJf6d9nsu6JDFTpo6dWpBj+Xco5YojR8EBQUhMjIS/v7+/DcvwmvkIBIfyhABjZ3Czp07+YAbdW9QNwIt7jEyMspXoyJWBTkF6j7wcvNGxEwPbuDIyNVeJXUFkDF1quCCwP5OSNkbgcTtYUjaGQ5DH4aeXXrBzyMAZv4GSNoVxg1pw88jYV/fBK2atMlXROQUqObd+FAkyMGQHOdkC1gaWGP86Am8pVF/YyUk7QjjhixiotQ9M2n8JG5oqi3y5Xkgg11rtT8szaxxJY9TePDXA9jaVkBMhidPn/JcY7k/f79nt16wMLJC0EBnNNyXq4uRN0Pndl3g6+YPqxijHB0bHYiERQxT6BSmTpjGDS4ZfNKF5NjHmcHSxBojhozktfOknaE8LTLK4RM8YGJkigF9BvK8VJnjzR0jvVtrjT9sDOwUxg8igxs9K1eXqnO9OadmjZrD0cIZQYNzdUnZHQ5TX4aGDRrBzz0AVpGG3FFTeTU8EAmrWEMMGzgiX7lkZS6AYQDjehDb5E/D4VjfHAbMENMmTQMzZUjeG56ry0R3ONk5Y8TQkVyXmFQvpBDPHWGI30rdgwYKdckr+NixY7w7idY1KOp+y/v8P//8g0uXLoHeo0FrGr8ShyBQFglo7BQUwSAjQv3ueY+CnAJeAYHeQQge5YyUz8KRuI2McgTqrQ/mBsHY0QCJ20P5Pz2/91k4qmb6coPgkmyFRl9EckNO98jgk+HPTJ+TNwtYt3odmAPjxpCeJSNCNXbP1nY8rZCBbqBaL7+3PUxqTQSZ8XvVF/jyZ+le8q5wRGdUhJujOyj2Tt7DxdEFgYOduA70POlSd10Q18XM3RANtuTqQi2W2EWS03CoZSHpsjOM54H0MvZmmDZpel4R2LxhM1gFhoSPK3FjSbo0/iISvl2lLqvICZ5I3hMh6bItDORgLH1MuC5xy/xzdCEjXG2JN1yt3RV2H1F5ho51y2FGxrfeh9K4DNflYzlddoej5tuSM3dOtEKzk9Gvl4sDw9zZ8/LpsmL5St611GCr5MTIKVO5+HaSdIma5JXDkng2ORIJU3cjrkut9wJ5S0hWLjFzPeHp4K3yimZqicTGxvK01OlOyqeEuCAIlCECWnMKWVlZ8PLyeq3vWsapQKcAIDo0Gp6dbKUaX7bBJiNh5mSC4IFuOf/49M9Pf1RDtnQ3hU9bp9fuUa2Y+tipnzrvsWfXXjBLhvobg3McDKVTabA7DAwYErflGjiSQWlVniV1mdRdE8xbItz47A5H+Ax33uVF4xl5D28PH/j1dpBaNtuoZROG+I8qwcTaCMEDXHOuy3QhY27uYgLfDo65+pODOxLJ8/vOW+/kFYETR0/wGnu99SE5hpcMf3B/N5hUMJL02y6x4nn+LByV06WuLDLq5Axk10PGuyDMN+K1fnyZwGCfEPj0tM/JM+lC3XTGloYI6pNflyZHo2BoagC/js45jofkNDos6SI/FiSTceSLI6BuKp6vHdkO8UAkQoe6w8TWCNxZZF+X5Tl6hhc35JQfciL8OpXLG24IqhiiUs1fJp/Os2bN4unNnTtX/rL4LAiUSwJFcgqbN2+GtbU1/4cyNjbGv//mDszK0yzMKTRr2AwODcxyDAnVSIP6Sn3UVPunf3r5P+r6kdWw67wfzA0v7z74qBI3pLs//UxePP/82y+/gxky1HwnQOqqoO6GjVIfdKWh+R0PyWt8KAoWrsZwrmHDa+J0jfLm1aECIipF5pNBF5qltIBDA1NQVxZ/fk8EfNpKtV4aj5DXgz6TLtUX+nGG3DBSS2F7GG8FGFgyKNLl159/5c/XXhEk6bIzDPXWhYAZMJDB5F1t8syyWz42/uZwirXmLSqet70R8O1rh+qRcQp1odlebq2tc9KjVo9PGycYmBig0cFIqZUiJ4daPjHTJUfK9ZQZ+cMRPL87tu3IJ+enH37m9+qsksqRDD3XhTHEzPTOkZ3DjXchhsEmwByeje2lfFC57I1AxS62aFArKZ8MVS6cOnWK5yMmJgbUpSkOQaC8EiiSU6DxhMOHD+PgwYOYOHEiIiIiFDbdC3MK/Xr2h3kUy/kHJ+NJXRe8Zr0nu0tHzviQ0UzcGQYrL1N4tXTk75ExqbUikBvGr69/na88H9x/wNOM+5+/NP6wPwIhg9z48/GbcmvcOcaHDPZnEYicWJG/R06HZFDrwrW5FWrH1c0ngy4M6D0IVtUNpS4XGp/YG87f591TNC4irwd9Jl12hMHa2wxeLRxyusPqfRgMcgqHvzisUA7xiV3sj6Rd4XyMImSAGwzNDJC8KzvNPHLIYEeMk3QhZyjTxamRBZLqpSiU0bd7P1jXNOJdZrxGviOM60K1+HyOh+TtCEMCtfAcjOGdrQtdq7cpCGamZjh7Jv8Cslf/veJp1nonkJcLOV1q8ZB+1IrKxyu7FRc+riIMjA2QsDlXF8dG5mitYDxJoXIKLtLYQq1atXhFR6w/UABIXCoXBIrkFPIS8vT0xPLly/NeLnCgmR5+a8lyMG+GZDK6ZBT6usLUTq7rYIfUl0+1at71kV3zrZIujS3U/yCE9zvHLpVq3A//yj9vn+SQoYma6ikZtE9C+XcyQGS4+SA2DXTulv5kRpDGEGz8zOBa15a/RzVkyyoG6NVVcZjm2bMyYBTEeHqNPo+EdxtHmDkaI2FLKO/qoHRzZFA3TrYu1eZKulDtnwxj5bneMDE3QUG6VM304c6HDDTpFjm+otT/nl2bzpFDNfbt5NAiYeWVrcueCO5MzSMYhvRXHNNn1vQ0GAdLg8Ckt3crR27wG2yVHADXZVc2r2xdqDUh63ajMQb6HveuP6ytbPD1zfzOmsqFZk5Vne8tcflMcqLSWIKCcsluSZHDsHAzgVdzBy6Dl0sMQ98e/fL9/tS9MH36dM4zNTVV3VfF84KA3hPQqlOwt7fHihUr8kEprKWwfvUHYK6S8Un4OJT3JVcaIk0zbHw4EvU+DkVUui/Cpnih2luBaPBpOBofjuLdIFaepryGTd8rp0ldF/kykH3B0twKoePc0PhIFO8TNzRmSNwZzr8n7QlH7NuBCJvqjbBp3qi3KRSNvogC9ZNXyZD642uvDOKOwSiAIX1m/rUQJIYPAttLU2TjN1WCkZkhHxehdKg7qt7mUETM8uFyqi0NQOKeCH6dpttauJnCu6UDN9bRaZ4wNTNRuqqZZk2FTXbn+aP+fRpLIIdJuiXujkDsiiDOK2KmD+puDkWjQ1H8XrXsQXrqrml6PAoGPgyTx01WiOz9d1fxMZrET8N43z7VzIP7u3L2TY5Fo+6mSojO8JV0WZZdLoci+VRZetanjSNv+USnVQQNwD/+W3G3jK2RHaJnV+RTZKnFY2IjjYuQLsn7IlF9eSDCpngjMtUHtdaESPKpXLLHfMjh0rOGHgxpb6Qr1EXdi6dPn+aOISEhQcQ4UheeeF6vCWjsFAYMGICNGzfiyy+/xMmTJ9G/f3+4ubkpXAlcmFO4cukK/wckIxoyyB0GxoyPLwQO9wAzMIQJLbQyZfAxZ3A2YvxZ42BLVJnnixrLpNk7NOgaNV3qHlFWIiE+ofAf4MAHS6lfPHS4B+9yMouUxkUqMEmGtzmDGWNgBgbw7OTMja2Vhylc61dAw33hfIbTqhW5C7Xk5R09fIwPAjfYFgq/Ts68S6fh3nAEDHADMzSEMWPwMpPkOBpKuhhVskTV+X6IWyzpEr+5EsLGusLU2FQ+6dc+B3mFIGCQI8iJGhoboHKaD2q+GwSTUGkhmYOhJINkmZMuhgbw7umK+C2VYBtkDpfatpwxzfvf8cnO19KWfTl3+hxnTS0O3/ZOMLY15K05/yHuYMaGnJGHiSTHxVjSxSTaGtUW+KFymtTyoe6sSuNd4OXhLUs23zkuuiZ8+9lxx2NowhAzwxu1VwXBKNiSy3cwkGR4mjFYkC4mhvBo6wz6vdiGWMCruT2anYnmM7LeXvZ2vvQ1vUBTrak7ycDAgHeRapqOeE8Q0CcCGjuFLVu2oHbt2oiKikLVqlUxePBghWsUCEZhTuHu7Xv8n5+mWBqZG8K3gzOYsxk3Zm83YTjbn+HhJIZn0xh+H8NwsAdD/wjJCDk2tEeFMEv4d3JGyDgX+Lr6K+XfNKk5PDpYIXSEO++ecm8jraDuEMCwvxvDdyMkGU+nMVwYwLCyKYOLAQMzN4Zfdxeex7prg/mK4+NHFMe8uX/3vvTcumDe5+3XVdLFijG81UjS5fEUSc7PoxkO9WQYEiXp4tzYAXZhlvDr4IzAYY4I9g1WqktS3RR4dLJB2EgPmLubwr2dpEu3YIa9XRkobeJFsi4NZFjXksGTDHcFE/h1lXSpR7pYMBw6oHh1741rN7guNAZBrSofkuFpAQ9DhncaM1waxPDXRAbidWscw6FeDL1DJV3cWzvC3M0Evh2dEDzSGd7uPkp1aZrUjJdL+EgPPuPMs4szl9svnGF3F4YfR0m6/D2Z4cpghrcbM7iTc3Azg3c7JxjbGILGYGj19L7P9imVo+mNKVOm8Py89Vb+WW2apineEwR0lYDGTkEdhQpzCpQW9YlT1wnNEGImRhhdleG/GQzIZEA6A1IZMCv7PJsBGQy/jGIIsmFg1sZ8KqRbKyvE105QmjUa0KaVtcY2RmBGBnAxZzjTN1sGpZmWLYPkkMwM6TyrLhk6A55H51hrHi7jpoLBbBJMXSSki1uSraSLoSGGxjBgZgG6ZDJ8M5zBx4qMtjHMHExgX9cMCXUaKNVl+OARsK1nDCNzAzBLY3haMFzoL6eLjBfpQnqRLmkMb9RmYEaGPG/20VZgRgy//fKbQjkU/8mEmaJi8wowMDcEY4YYWTWbEZULpSuTQ+fscrkzlsGWWnQOJny6rUU4Q4e2HRXKoIuD+g2GTU0jmDoYgdmawMOc4ZwiXUiGTJc5DBPiJAfEeSdXgKE9w8XzF5XKKcqNM2fO8HKtXLkyKD6VOASBskpAd5xCdrcQ/YP3JiM6P9vgkDFV9jeb4d9pDDEuucahYwflxmfxIinmD8lwsmT4ZXS2EVWWPl0no7qIYX5yrgx6X9lBcaBoUJWeob/JdRiwQAVdMqRad6Bdrpwhg4coE4NZb8zi8/tJhret9C53oIXpksUwgzs5BmZGhl65LhRDyNVFmhpMz42MY8AcFXSZzXBnAkOcR64uPbr3UKpL5uxM7mhJhpUJw+3xKpbLHIblTSUZNFOLpuQqWlCoVLCaN27duoX4+Hg4OjriyJEjar4tHhcE9IOAcougxfyr0lJwcpS6PwZSTZRqtWSMCzJwsnvpkkGsaCsZh0WLFinN+aaPNnEjSIbnypDsmq0sncLOcxlmxucaOWVCqBZJ8XHIwA2spoEukxgqmElyZrzxhjIx2L59O5dhY8pwmXQhZoXpILs/h2GWCrrQfP2IbF0GULlQS0CNcvlnKoN59lhDQeXy7rtSUDtbM4Ybw9XURcVyUQpSgxvDhg3j7BcuXKjB2+IVQUC3CeiMUwiLqgIrw2yDQN0EMgOmyjlT6s8mQ7zugw+UEr946SL/Z17bmgHz1JRBxjCLobIrdW9ZKZVBN6rE1oaXpVz3iio6yJ7JZDjYU3IKmxWEq5YJPnhAioT6cUcVatWytGVn0mUuQ6QzyTGUJZnvTGEgKsfWhr9NNit1y2UOw9aOki7vr1I8ME9Ct2/bxstlY7vslogsn6qcSZcMhsouDEYW1vl0KK4LNLmCFmympKSIOEjFBVmkWyoEdMIpXL/xNTcKp/upWXuXNxqZDCOrM9g6uisFWb12Apr5F0FGGsPPoxhMGcNn+z5XKOfqdWlw9ssBRZCTwTAohsHdO0ChDLoYUaUGkn00cG4yZmnSOIYRY9i8Nf++DyTj3JcXeLl8M6xougyMZggMjVKqS0LDFmgTWDRdaJIAzRjbul3xTCqlwotwg8ZcaMGmra0tzp07V4SUxKuCgO4Q0Amn0L5LTzT01KCWKDNwdE5j+HMcgyFjOH/pcj7CD/9+wg1ckYw1yZnHMDiGIap67Xwy6EKj5m3RNkDNLhB5PbJ1uTuB8emrBw/l77t+8u9Trst16jaiAfG876v6fT7DoGiGuHrJCnVp3Loj2hVVl1SGp1Ol1sIhBbo8ePSI68LHd2gQWdW8531uPkOvcIb6CsKmK1ROixdls5OWLFmixVRFUoJA6RAodadw//5fsHaqiE+pG4T6rPP+s6vzfS5DfQ+Gjtn7F8gjnZmeAW8LLchIk6ZFMlMbXM+zB8GDh49gaWOHre21IGceQ203hp79BsurwT/PnD0XlazkZv6ow0j+2VSGX0fRGgY7KNqDgLrjtKJLFkN1R4bBCjYMmjwjHdXss8cqVB2vkNdB9jmN4euh5Hys8dNP+XeaywdRyxd2797NnVtycrKYnaRltiK5kiVQ6k5h5ao1/J+Jz2qR/YNrek5nONePwaCC52uhoClQX8WgaD6/vdAZOqrIXsRAC8/eSMt4rbSWvb0CNjQuUlTnRnlIZzjUg8HIxv21ncRoFzAHz0CsaKLBWIIi3RYw2LP8uix96x04GWvBWJPM2Qy7OjEwY5vXoui+fPkK9s7u+F9DLekym8HTiGHBkmWvlUtJfaFtYGlnNwcHB76os6TkCjmCgDYJlLpT6DdkFFr7FaE/Wd7QUU1zttRVcfBQbiC5a9eugTFz/DdNjdkz8unm/ZzJkFqHIbpG/Gtl0bJDd3QL0Z4uz6dJuly5ej1HzrkvvwRjllKLqig1a5lOmQyT4xiq1Hp9TUSLdl3RrZKWdElleDiZwYAxfHnxqxxdLl2+AlNzC77ehK93kOVJ03MGQ3o9hoCI6jkySuPDkCHSHtsFzbgqjXwJmYKAKgRK3SkERcVhaXIR++DljUgmgx1jWPvBphz9Dx05JrVGtFGDJ1npDPu7MBjbeebIoA9V6yQjK0FLupDBT2UIsWBYLafLzk+lbgosLGJXm4zZbIY9Xcj5mOXoQrOOImLrY1mK9nSh1dUBZgxrP/woR87GTR9J5bJIe7p82JrBwNQiR0ZpfaBNe2gv6ObNmxfr2onS0k/ILbsESt0pGFWoiL1dVBwwla1opQFJZX9zGRLcGEaNz91/9701H8DXVEUDl22MlaafvaKWZuRQn7tsbSt1Udm4B2F/Vy3qksHQ1Jth+NjcgHVr1m/gsaD44j6ZYVd2VkWXTIZzAyRdZD9zivnj7BuBvZ21pAsNhqcx1HdleENu97VFS/4HimdEU30LHUtSUZfD2dN5ZbqU5vm3336Du7s73/bz559LfpyjNHUXsvWXQKk7BTKs12gWTSEzT17NZLg2lOFYH4YTfZX89ZPi8bQPYqid0DCnVAaPHIfkiio4hVkMNOvneF/pT5mcMwMYtlEfOWO4decul3P3HsVvMsSfY1VY8fsGw1UVdLkwiKGVP0NKs9w9p/sPGYXGXip068ySVhUXpsvZAQybO0i63PvrAdfl+++/B2MW+GeKCt1tqdLiuQLLpa+kb9tAhhr1cjfBGTxiHJKoXApbMzKL4d5EhmOFlAvpsqWDNAPth1IYbM75weX5QCG46bcyf/78PHfEV0FA9wiUqlOgWjb9s1Dcn8KcAtUkbw6TnMGpfgzK/i4PZugQzFA3sXEO7W59BqNrsGpOgYzPyb4MJwuQQTXrXV0lQ/rnbckp3LtHgfCM8McYFZzCTIYbKurSLZQhOrZOji79h46Wpu+qaEhJj8J02d1N0uXKtZtcztdf07oRQ2n1MtXQlbVE6Hoqw9UhhZfL9aGMT9WtWT93+mv7bn3QncYt5hYiYybDX5MkGQXpQtONt7SXOYVfcpjpwocNGzbw33rbtm11ITsiD4KAUgKl6hQoV8zSBQe7a6mbglob8xia+TCQ8ZQdS5a9iyBVp6Oq0k2RwfDDSMmQvvjvJRdDISGM7b1wopcWdclgaOnLMHjkBJkqWPbOe/CiWUFa7HI5P1DSRSbkwYMHcPAKxcFu2tWlqRfDiHFTZGIwZ/5ieKvafZTtgArs1stkIMdAFQ1dPJ49e4bw8HCYmJiAWmPiEAR0kUCJ/PcUFPvIN6wq3qYpierE7imo5prJ4GHEsHzFqhzeB2hzeDIU2pKRznCsFwOzcM6R8fLlS4RVq4f3m2pRTipDuDXD4v+9kyNn6zYp5pE2B5r38VZPbrgLmvZaqUodvNtYS7rMYng+nSHEkoHGd2THmrXr+WJDbeqypZ3uOgWZ3mPGjOG/x6ysLNklcRYEdIZAqTuFLr0HoYeKXQgFdmPIHEWmZBQ+P5i7R8DVq1fBmKlWp3Fm1KMpqa+H6aYpqVrTZRbDqxmSLpflpqQeP34cjBlL3W2Fde3ImBR0zmCYG8/gH17ttR9lk9adpJDfKnTtFFouqQwPJjM+QC4/JfXM2XMwMTXH/QmqdbkVKidbl4qBka/pootfPvnkE95i6NixI6iVKQ5BQFcIlLpTeHPZ21JtURvTEmWrWs1d8eOPP+Ywvnv3Liq4B+JjCrimjWmp8xlCrRiGjRqfI4M+zMlaCBtqkVDY74IMsSr30hhuDKFw0DavLcSjmUEV3Pywo4OWdJnHEGlLs7Vyu3VIl8yshfCmoH7a4JUmbfRDrTUKLS47/v33KaztHPGJNlaAE9M0SZcJU2fKROj0mcJ8077mFhYWoHEccQgCukCg1J3C5StXQSEjfh6phdriHIax1Rmq180dzJRBbt+1N1IovlJRa745NXgjHPwitzVCcm5+8y3MzMxxeZBqA+cFOo65DAOjGOokNZWpkHNu26kHmnhrQRcypNktK2qByB/ffv8jd9Za0WUO462OBk1yZ1HJZKU0a4vWFKSwqF17sxj+my61rC5+lT/2lUyerp0p1PrYsWN5d9I77+R2E+paPkV+yg+BUncKhNo/JAppdYsYEI8MXDpDgBXD7LkL8pXgjl17UMGAgbZ0LNLq2dkM2zow2Dp54PGTJ/nkOHv4YF4DLegyh8HVlGHu/MX5ZGzZthO0n/SDSUXXZXMbBruKwaDB5byHma0zFiVpwWBnMZ7f+YvezCsC23Z+BgfG8IjKpSjdYbMZdndicPQJx8OHD/PJ0fULH3zwAXcM7dq1A41PiUMQKC0COuEUJs9IQw1HFWe6KOt6SWO4OEiqKf7wk+LpiNR9sU/VGTXK5MxhvGbbpJXiHd5GjJ2EGk7Z3UeaGrnsoHtmRgw3v/lO4W+DdDnSu4jM5jK09Gdo3razQhkjx09FXZciOp40hh9GMJiYW+H6DWnKq7wwin9EulwYWMTW1TyGJE8GahHq60GhuIODg1GxYkUxO0lfC7EM5FsnnMK33//EDQNtNq9xLT6D4a3GDIYW9kqLJbRyLQyvUoR+8lRpEZUtY7yGq0jQja+/5brQdpQa65LJeGvD0s5FkQh+rXLNBtJ+ybRXsjIHVtB1ikc0iYF0+XTPfoVyzl+4xHXhe2Vr6uAyGTLqM3j5ByuUQRcphtS46kVoXc1ieDGdwc6Y4ZMdnyqVoy83Bg0axLn/73//05csi3yWIQI64RSIJzOyLtpA8GyGeDeGgcPGKC2ed1auhrNBEWqkFIW1kHnw1EdsZu+JbUUZPJ3FUNuZgWrqyo6FS5bxLhmV1isocg7pDAcKCQnx14MHsHDywfaiDGqnSeUyaoJyXbIWLeXOSeMB+tkMe7MXE5aVjpd169Zxx9C9e3dlPwFxXRAoFgI64xT6DBqhWsgDRQaOarGzpK6jk6fOKAX1ww8/8lXHf2lai88eyKbAdwUdnXr0l8JqFLbqWJEuqQyPp0i6nJeLKJpX3uXLl3koiieajpFkMIyqyhAZWz9v0q99b9+1D5r5qhCKQokuv42RdKEWlLLj4qWvwIytVAsRokhOBsOYagwR1RRvfKRMrq5fv337NkJDQ+Ho6Ch2dtP1wipD+dMZp7Bl61ZeM9JoIVM640H1rFwDC4xISdMhA6PiNI/+uYDBgjHMyVpU4E9g/YcbJV3maNC1Q1FLOzOYOnjhiYKBbJlgapH4hVXDm5pGMp3D4MRoYdxyWZIKz2vXb0AFWkFNxljdLiTaR6EzAzOzU5i2/EU37wAsb6TBoHZ2nrxNGN55f6189NBdiAAAIABJREFUkmXiM62C7ty5M/890doGcQgCxU1AZ5zC77//DuMKFXGmrwbdO/MY2gQwtGzftVBeYydOQ2gFDaZzpjK+yIrWDVAtvaDj3v37sK7gqHrEVPna7zyGxIoMnXr0K0gEvzdy3GTE2GnQF0+tkclUgzfD9eu5ezUoEvjw0WMYGDJ8rskA/TzGg/f1HDBMUdKvXRs4fAxiaYBe3e1FUxl+z26N/Prbb6+lWZa+7NixgzsGCsVNFQJxCALFRUBnnAIpWK12AobEqGmws2uKLiYM761eVyin46fOwNqI4e54NQeCMxjeacTg4RdaqAx6ICSyGl8zofa6iAypNaKKLqfOfsk3rvlJ3QH6bF38I2JBeycUdvhWisakGhrsjjZP6jpau/7DwkTwzXdoE54/xqlfLhSOIyi61mu7uhUqUA8fuHTpEjw8PBASEoI///xTDzUQWdYHAjrlFCgujo8JA4XJVrmrIp1hT/Yg49Nnz1VizozNsa6Vml0VGQxV7BmGjhqnkoy33n2fB657MlU9XfZ3YzC3sMSjv1ULfUDTOT9qq+aMqkyGGHuG4WNyA+0VpNTbK1fzclFrFlI6w/HeDNYO7rhz915Byefco5bLbtrDQZ1V1FkM/pYM46fMyEmnrH/o1asXbzWsXVv2usvKetnpg3465RT+efqc/9ivDcs22Hk30lHUp529BaObT4jKvJObtZNCNtMq2rwyaCMf+e4c+pzK8Et2F8WFS1dUkvPXg0dcF4qmyo1cXjmKdMlkGBfH4BmgWmuEMtK4VUd0prDgNDU1rwwlutB0WSvGcPLMOZV0+eFHacowX/iXvWHOa7Ly8qLvc6WB7IiqNVSSQQ8lNW0D2guDz6hSUZcHExksjRgOHjqispyy8CA5BKoQ0HiDOAQBbRLQKadAijn5hGJhorTfAG3cItsk5mgfhj+pa0HemNLnWYzXyN9cvlJlLl9kb895b4K0aY9MBsm7NJiB14jlDd1shu0dpa4QlYUA8AuP5YOnXw9/Xc7h3tJmPnl1eTGD8RDfK1bnRhItTN4n23dy4/ByBsPR3rm8SBdazPfqjTxObjbD+lbq6UJdTIFRNZAZz/D9yPy68JXV8ryyo6IGmDO8vXJNYSrk3N+6Teo3JydMC/Pky4XCe+dz1hkMq5ozWNgoX5uSk3gZ/ECr0MPCwuDs7CxmJ5XB8i0tlXTOKdCK4FhHhpvDGb7oyXCoF8MXvaQ59b/RrmbyTiGV8d3BqMZ07foNlRn+eesWGLPEl/0YyECTDPo72FOKx5/PKcxl6BTE0KhlB5Vl0IOkSxU7Burzp7Rlcvb3YLhNYxp5dLk1TjLWP//6q8py+C5pRvYKdaE1FS8VOIXeYQzJzdupLIMeHDJyHCrbMfw+No8u3RnuT8yjS5q0cRKVy6O/84cCUSb4u+++g6GlE471lpyCjBexO91fgVNIZ+gSwpDUpLWyJMvF9ZSUFF4x2LdvX7nQVyhZvAR0zimcOnWK/8BB0znzdlXIG1GqmWYwLE5kCKlcGy9evFCLVIMmrTE4OjuiqXxXhaIulyzJWG/+eKtaMg4fOSrtYEZpqqDL240YfMOqqyWDHq6X3FxaqU3RWQvShfilSbrsVrKKWZlw6p4xNWL4h9ZFUJ+/vBwF5UIxk1z9I5Qlp/R6dGxdaXUzbSIkLyNvucxieDqNwZgx7Nl/UGl65eUGOQRywm3atCnzA+7lpUxLS0+dcwp37tyFpbMfdnVSYcBxPkNNF4Y+Awuf8pgX8Jz5i+BmqsKMmjTGI7gyEydQTVad49+nT+Hg5qXaiuD5DJXtGUaMnaiOCP5sasY8hNqqwItq8MMYmKEtfvzxJ7XkvHwFGJtaYlMbFQbo5zPeQho+RhNdsvhmPLwVldfZyHdRpTF8xXeMM8eDB/oXAE8t+Co+fObMGb7QjbqU7ty5o+Jb4jFB4HUCOucUKHvtuvRCCm1OX1CY61SpC8aS5tDLbajzunrKv/30y68wNzbA1cHZNVJ5gyP/OXvAtFrtROWJFXCnSav2fG9i3vKRT1f+M/XBT5Nq8Hv3f15Aaopv3b57j9cSvyosZPcchpFVGOo3bKk4oUKuUvdZJxrULmh2kFxr5MDBLwpJMf/tR4//4bpcGVJIucxhGFGZQos3y59IOb/SrVs3znD9+vXlnIRQXxMCOukUPtq6HY6M4Z+CpnNmMGxsQ7VeE0305u9UcPbA4uRCWgtpDH5mDLNmz9VIjiw0NO089toYgrxTyB7ItrFzBEUN1eQwtLTDssK2NZ3N4GfFkD5Hs20gd+zeW3i5zGb4tCNDBRdfjUNYM3MHrGlRSIuEwnEbMmQoCJOuCb+y9g7tzUDdSf379y9rqgl9ipmATjoF0pl+0Ad7FLDCNZ2hVxhDfMMWGiMaM2kGajkXYKzTGK4NlWrwNF1W04N0OdmnAF0yGDoEFW3AdPTE6Yh3LUBGGsPVIYxvnPP1t5ptGv/33495uVwvqBZP4bj9GFooCcetCsOho8ajknX21FR55yn7nK2LmakJbtz8RpUky+UzP/30E/z9/flit2++EZzK5Y9AA6V11ikERsZiDIVTVrQjV6o0q8aeMXy8fZcGakuvXLl6nRu5v6coWUWbwbCyGQMzstJYBr0YU7MBptVU0iKhkBNTGZwZw47dms8eOXrsBNeFD2gr6ovPZHizIYORZdGmb1av1xCTla1upnDckxnfNGfjZs3j9Hxx6LCki7LYUXMYFiYxOLh4FqlcysPLtGFPy5YtOc9NmzaVB5WFjkUkoLNOgQK1OVGYaznDQLNNqEuJplle4RvqGOLWrVsaI6CAc+aO3tjTJbeGTWsFSMa/06Q+bap9Dx75+l7M6gpctHQZXyyGBbnTKmW60DqCc/2l1siz55q3Rv766y9YuQViL60Izo4f9Hy6pAvJomm2FFp8yCjVVjEr0zFrwWI4Gr6+D7VMF1pHcLiXpIuy91W5fv/+fVBww/1y5SKvy7PpDLVcGAaPUG11uSoyy/ozFIrbyMgIw4YNE7OTynphF1E/nXUKFKiNMVNpCmQqAxmFPd0Y1rdh2N6Z8XDOdZOaFFF9oE3nnjxoGyjM9SwGWmi2pjXDhnYMOynCJ2OgqaVFOS599RUYs8Kj7O0zX81g+LwHw7o2DDs6MzTyYYirm1QUEfxdGqBvQ/sdky6pDJcGMaxtzbCxHcNH7SVdzp77skhyzl+4CGMTM9yWxShKY6B1FzJdUrwZqtaML5IMejmpaWvepcYrBakMZ/szrGvNsKk9w8oWki5Xr6m+NqXIGSoDCVAgR1tbWwQFBYHCcotDEFBEQGedAoW59g2tKu0RnCmtzH02TZqbToaiIg3+ps9RpJNa19Z+sAEWso13aPP3GdkyZjFeU7V08dPK9D7fkGgpNHT2TmlU26UaNs2wcjZiWLA4//7FaikC4L3V6+FmxgBasEa7kcnpsr09g5mDZ4GhxVWV5+TmzbuiZF178rrYMYZ5C/LvK61q2rLnNny0NXdQO7tSwHmlMnzSjsHUzkPttSmytMvzmdbzdOnSBWZmZtiyZUt5RiF0V0JAZ50C5XfEmImItn+9C4kWNP00isHM2ADnL15Sopbql2/fuQszcwsc6ZXb7cLDKWQxPv1S2f7FqkuQnhw0Ygxq0qC2/BhJGsOdsQzM2AJfnr+gbpL5nqd5S9Sy+SLvAH0W4y2I1p165HtHkwvUnVbPLc+U0VSGF3xarRkuXryoSbL53iFdKHSHrDtMVi5NffR7L+Z8ipbChcWLF/PfyogRI0pBuhCpywR02ikcO3Gab2rzB4W3kK1ozWB4uzGDnZOb1rgGR1bD+Fg555O9WtbNiGHlKu1Eorx4+Rr/J/x1zOu6rGjC4FzRV2u6+FWKwRQa1JY5n+xBZwcThvfXaGfe+sWvrvKQ3RQ76rVyacTgGRwDGtzUxuHsHcL3d87RhWYfzZG6jlatKTxMujbyUJbToMWYFSpUQEREBP7++++yrKrQTQ0COu0USA+qLX7YWm7BVBpDSkWGvoNHqaFmwY8uXLqcr0WgbhC+liCd8fg7JFubB2OGr69uTmd8SmyfgcO1JmbewjcRbJ5trMkhpEstB9LlwSPt/eNT7KjPaCBYtpBtDkNVB4Zho4o2KC8PYsGS/8GaykC2iDGd4WB3BkubCrh77778o+JzEQh06NCB/5+JxW5FgFiGXtWu1VMC5ubNm/xHV9D2kkpeRUrzdlJoaKr5pjI84juGMZw+e17ZK2pfv33nDs8fb5FQvJ0Mhtn1GVx9gtVOq6AXkpu1RY9KuQPBVNOmjWUuX7tZ0Gtq3bt+/QbXRTaoTbpMiGWg1pA2j/bd+qCJd/ZaAtr9jLrBGMPxU2e1Jub8hQs8TT5GQi3FOQyDohkiqtTUmgyRkERg0aJFnHVGRoZAUs4J6LxTOJwd5poGmTGfYUVjBme/SK1vSVildhKGUIC8hVLtmgwc7bWszePo0WOSkSPHk8X4/som9l7aFMHTqpPUHGOrSbo8nyEZ601bNF83oCiDn+7azXV5SqvO5zEsb8xgbOmg6NEiXYuKrSd17c2Xptea0XqOXXuKlKZ4WTGBP/74A8bGxvD09NTK5ArFUsRVXSeg806BAAaEV0WXIIaHE6QVuXPmLdA6140fbeFG7puhDFNiGaycfbTez0p76/qGRKF7CMODCZKxfvN/b2ldF9r+kpwa6TK7NoOFQ0U8ffZMq3Jom2AP7wAMjJANMDNkLSz6rKO8mdywSSqX74YyjK7CYGnvhhcqbCGaNx3xXTUCtN6F9oE2NTXFkSPla+Mi1QiV/af0wik8fvwYbj7BYMwEAwYPLbZSmTx1OpiBNSzs3XD+vPa6p+QzfPfuXVg7evD9HIYOK76ZHzNmpvJ1Hk6egSiuEAfPnj2Ho7svaBvN8RMmyaup1c+jxo7n5eJUMQAUCVQcxU9gyZIlvGIhZicVP2tdk6AXToGgPXz4EF999VWx8yMDSs3o4jxopse1a9eKUwRP++rVqyAnVJwH6UKLoor7oHK5d0+1vZ6LOy/lJf0rV67AysoKcXFx+Oeff8qL2uVeT71xCuW+pAQAQaCUCLRo0YK3Gj75RLvjUqWkjhBbCAHhFAoBJG4LAoIAsHDhQu4YZs2aJXCUcQLCKZTxAhbqCQLaInDjxg3Y2dnxxW6/qrGPuLbki3RKhoBwCiXDWUgRBMoEARrba9iwISwsLHD8+PEyoZNQ4nUCwim8zkN8EwQEARUILF26lHcnjRqlvcgCKogVj5QAAeEUSgCyECEIlEUCJ06cgJOTE+Lj44t9lltZ5KerOgmnoKslI/IlCOgBgf/++w/16tXjrYajR4u274geqFsusiicQrkoZqGkIFC8BN58803uGKZMmVK8gkTqxU5AOIViRywECALlg8CxY8f4YjfRnaTf5S2cgn6Xn8i9IKBzBGrXrs1bDRcuFH3jKJ1TrhxkSDiFclDIQkVBoKQJyBa7TZ06taRFC3lFJCCcghzAo8eOoVGT5hg1Zixu3bold0d81JTAoUOH0bRFa4weMw4//fSTpsmI9+QI7N//Oeo3SEb67Eyd/p3SwLO1tTUSExNx/77YFEmuCHX6o3AK2cVDRovCTYc4G8GIMZhYVsCwEWIOdlF+vYOHDONMq3ubwcJA2ot69Fjt7cxWlLzp67s9e/fhTGv4mcPKiMHQzAYLFy/VWXWeP3+OypUrw8DAoNgiD+us8nqaMeEUAFSPq8n/0VYPqYZrixri2sKGmNQyEK6W0p4HI0eNEfOw1fyBV64Wy5numVIblxek4OK8ZKR3DIWTucR0+MjR+O2339RMtXw/XqN2Xc7004m1ONML85KxoHs4rMjhMoas+Qtx+/ZtnYQk29ktNTVVJ/MnMpVLoNw7hffeXyX9o02qjZOzG+CLmfH870xmIg6+EY9JrWgfBwYTaweQIRNH4QTeXbGSM/tgRBxOyDE9nZGIz2fUx4y2lWDCqOVghRGjxhSeoHgCi5f+jzNdNzwWpzISc36n9PngG/WR2TkMhozBwLwC5hfDZkfaKIKDBw9yHZKTk7WRnEijmAiUa6fw4K8HYMwA09sE4+ycpJx/NJljODwrnv8D3lzaCBNbBMLZQqqR0SCaOBQToEBpzMwG87uFFcj0UlYK0jtUymk5rFixUnGC4ip+IaYGxryldW6u4t8pVWguZlHLIQI2RtLvdNmyZTpJr379+tw5nDx5UifzV94zVa6dwtFjx/mPc9/0eiAHIHMGis7Ucjie3gBJ4XZw9dD+vspl5Yco27uZujYUcZS/Ri2HY2kNkBRqC2+/wLKCQOt6fLhhI28FnM1MxKHslqw8R/nP1HIgBxEfYgNff91lSiG4qQU+f/58rfMSCRaNQLl2Cm3ad0L9YGucSM/tNpL/B8v7+dL8ZES4m2DQ0OLbRrNoxVn6b7fv1BU1/SxATjQvP0XfyYBV9TLFmHETSz/zOpqDTl17opa/Jc6r4GjJadDvubKnCcZP0u3poNRSMDExAa1roAFpcegGgXLtFCJjqqFbbTeF3RyKDNj1xQ157WbDxk26UXo6mIvAShEYkOD1Wr+3IpZ07dCseByZlcCZHvzisA5qoxtZiq5aA8NSvEAtK2UsZdePpCZg56Q6vGVx4uRp3VCggFw8ePCAx06ytLQUobgL4FSSt8q1UzC1sOSzjOQH7mT/XHnPR1MT8OGI6jA0swZtNiIOxQRoKi+N0cgP2udlKftOTDeNjAUztcHvv/+uOEFxFSERlTGmia9KjvZYWgJWDqrCHe2rV/oDb9q0aTzPixcv1p9Ml9Gclm+nYG6JSa2CcHJ24TUwqqUNS/GBT0BwGf0paEctUys7TGtDTAvvkiNnPDTZG5FV4vDixQvtZKAMplIpsgpGq+gU6Hc6OMkLUVVr6B0JCsVN6xko6urLly/1Lv9lJcPl2imYmJljsopOgWZ9RFU0RfdefctK2ReLHuo4BRqMruRqgr79BxVLXspKouo4hQtZyQhwMMDkqTP0Un1aZ0FjDPb29jhz5oxe6qDvmS7XTsGtohdGN/HDaZrVMSuez0CiPln6o9lIdI26Ouj7p5PrwJIxbN+5S9/LvFjzb2xRAdPbBvOuDoVMs2fPEN8DM+rD0phh40ebizVP+p44OQXqPqJWgEKm2b9TGmQ+NyeRd8PQLDB9PiZOnMj1WL58uT6roZd5LxdO4d9//8WTJ094k1S+WVqrXgK61nIF1VgPvFEfe6fVw6eT6mDX5Dp8kRU5BOqjpVkfa4ZJK3Rlpfzs2TOeJnV7vNKnzluZAkU4k77E9J9//gFtsiKvf0XfIExpFYhzc5L4oqp92Ux3T6nLmZJRkzF9Z0BlmBgZ4MHDhzw3T58+5WnSTBT5NIuQVb15lX6X8kzlM04DzeOa+kK2RkH2O1XEdM2QqrB3csHvf/zBk5D9TvWRKe0BTdNWExIS5HGIz8VMoMw5heMnT2HsxKlo07kXYmomIii6JpiZIxizhGdwNMKiq6Fb9x6YOnUaPH0C4GJrhpRod/i7WsPQyIT/COmH6FzBApHeFRAf4YZu9f3QMMYVjBmhbfuOCK8cBzMHb56mjXsQ/CNikdi0Hbr0Hoily97Gt999X8zFVrLJ7/v8ACZOm4lWHXsgKi4efuGxYMb2YMwaHgERCK8ci85dumLCxEkIjawMOwtjNIh0RaWKNjCQY+pib4nKfvaoH+6GLvV8UT/MmfPu2r0nQqNjYWTrDsasYOMWwJk2aNIWHbr1wftr1uH6za9LVulilvbZ3n2Y+kYaWrTvhpiaDeBdqSqYBfGwhotvKKrG1UHXbt0xdNhw+AWFoqK9BRIj3RDqaQtmmPs7dbCxyGbqit4NAlAr2AFWtnZo0rwlKkXHwtSuIv+dWrv6IzCqBuo3bIX2XXtj5arVuH7jZjFrWfTkKZAe7c/g4OAA2q9BHMVPoEw4hXNfXuDGw6qCE5iRCYKtGXqEMixLYXi7EcO3wxj+GMOwswND+xBptScZfgPG0DGcwcNauja4GsP5gQy7ujBUdpOutQxmiHbNfcfOiGFcLMO1QQy/jmI40oNhZROGGTUZ2gcy3sVkamEN36BwTJqemlMLLv6i1K6EC5e+Qot2XWBj78JXfQdaMfQJZ1iUyPB+M4argxh+G83wcVuGbmG5fMwMGTpHsJy4UeNrMZwfwLC9M0MNT+m5FkEMkc6571QwlJheHsjwyyiGvV0Y3mvCMKE6Qxt/BitDBhNzS/gEhiE1cz5evtSjaTVyxXL1+g00adUBDq5kqBkCrBgGRjLMb8CwtjnDhf4Mv41i2NGBoaFPLh9TA4aukQxu2bG4ptVjuDqEYWNbhprZTJsHM4TY577jYMyQXo/hfH+J6f4uDCsaM0ypwdA2gPEpq6bmVvANjsDUmelyudTNj4MGDeLM/t/edUBJVWTtO6QhDznPgERhBUEQEBRUgmTJQVGQnHMOwvRM90QEASOKiyAYVgEThhVZV3dN6xoRFdPqmn7FhIppv/98Va/g2Xa/1zN0z3Tje+fMed099Sp879a9VbduuPnmm+Ozg6dQrxJaKPz7xRfRf8hoRSx9Ggj+PFDw5RIB1gmQLUBAgFwB/IIHLxVUKC2onCxYcZ7gyQkCXCXYNkSQXErw0nQB8gTIPPFcVk9BUpLg2CrBr2sEd4wQDGiuJ96wloJXZ+g6kCVQfzkC5Atenia4squgpZrEpeDz5+C7779PCLJ59bXX0L33IIXpkMaCLf0EP64MgWm2YOdwQZWygjoVBau7CfaP03jcPlxQuqTgFeJD/A2meYKl5wrKlhL8tFrw05WCXcMEgyxBPaa14PkpAlxt4Ulc+XyO4PUZgmWdDaYl4AvkgOqmRLhefe0g2nY+X2HKhcPNAwQ/rLBhynGS9gKCPw8W1CgvSK0sWHiO4JnJAmwQbO6nFzGvzdQ0dhzT9YIr2grKl9Y0T1q9ZbBe7FDwENt35gbRqQ3TpZ0FjcuQpssgPTMrrq3AnnnmGZQqVQqMnXT06NFEePUJ2ceEFApcJ06YMlOtYM+rbRG932LmPgHWWn9Zgo8XCWpbO4HcXoJvllsCI1vwxmzN4PeO1ozn+HN8Pl3/1quxoFYFPTGVkMkUHJ4jOL+RfnZCW6ssGZ9pN8NqY61g7whdrnSlmvjL7r1xTSQDh4yESGlc3FhwkAydQpV/xMKMLVtAxpSWoseV1cPC1GI0/5qqfz8w3mLs5jmDqV/QvaGgRXWLEZIhBgTvzhO0tXZnszoKfrnSEibmeWLKsumC7RcLyoqgcq007N57X9xiyh3N0FFjIZKM3qnWIsIabzCm/5woaFFDY5ffW/AdBTEXGTmCpybo3/eNtd6HwcRgGhB0rC8grSphYS2IXp0paG3tciefJQDnRgg6/d8awa0X6zZqNmga13T67rvvomXLlqhTpw4OHz4ct+8+kTuWcELhzTffQtU6DZFW2mJcXGGRYQRPlDxBXi9N6DM6CI5yknGyGKGRqyfhtLNDMC9TV4bg6+W6jpsH2cqxvVzBS9MEjaro3cdbc2z/N8+TmZKpZgtu6KvrGXXpuLijl4MHD6JSrUZoU0nw9ESLWYfCNEtwXX89jmkdLMzJuAym6wU1ygkmtrPqMDjY7xmCH1cLkkvqXZrCh/9ne3mCgzMF1cvrXd2RZXqX97t3S8aaJfCfb/VlVvxFr33rrbdQrmodNCkrOMhdKHevoTANCK4foMcxpb2NqRNT0o9PcHoNwXTSKeuwY2k+s6xf17FzmA0ztrde74qrlRPUqyT4bLHt/+Z5tkNMcwWruuh65i9eHnd0au/Q8uXL1c5r06ZN9p+9z1FAIKGEwksvvwqpUAPn1LJWUtwdGMI2dxK4XxDoqYk7r7e14jKMi+UyBU9P1v8/NCvEZDV18Z4lmN9Z0KSqNUlZv/l/QPD9Kr1rKFdK8OK0EzuE42VM2VzB38brNgcMHROFVxedKngoLlIK3etZzD0cpnlanUGVBNUTvxGwHGOG4L8L9fiUWi2YARoceM8RLDtX8KdaFpZ2TP2C71cKOtYTlCoheJkMlcLc/jw/85lswTOTdJu9BgyNDiBRqOWJJ/6uDnf7NrL6GQ7TDYJJZ+n+/2WUxayD6NTsvD5aZBO+wVjwe66Au4Ez64RYnAT0zsucPygVVDhMs05g2n/IqCigEbsq9uzZowTD0KHx8+5jN9qiqzlhhMLWP9+qCGDZOZZ+1D55zCSxBAK30WRer5Phcydh/m/uPq3C6NfcYfVlyrLOPF3fbqqZgic4+3GVZnJs8zau1Lh6Ns/b79w15AhqlxCUKlcJP/5YvEHAbrJySWzoGUJwmn5z/OkaL+qtqXILyaQtFcb4Mx3Gb+r0aaFOvO6/NAymmwQzz9a4P8AyXMma5+33LMHRFYLGyYKUGnWLXSe+fcdORXs5F7hjSpUPz1cOhcM0R9CsukDtykg79nEHf/YJ/m+JxouC8jdqIpYlneYKlnTVZXjG9jtaNnVmCb5ZJjgtWVA7tQmOHv2u6DhSAVuiyW3Hjh1RuXJlvPjiiwV82iseCoGEEArvvPOuWs36ujswBxJ0niDjQk30tCIKybx8gi+W6jJqZe+0ojWTJFdw8emCnk0c2s8WrOmu6z3Mg71wkzhDr9pOryg4v8/Fod5Jkfz2wYf/VczrynOtg0sz1uD7egF1/ErIknmFYs4Z+kyAZZQaLRJM/YIRrQQDWoQR3OxH4IQK8G2q54IFsulrhjYEqFNa0LP/sCLBL1Qjetcl2NzHwokC1fTRfl8vmNpeY/pVKBUZy/r0eViZkpZRhP0swF6X/XOWgAsd0mrIxRD7ExD4LtBtf8rdRzhMMwU8a6hZStCt14BQw42r34x10pYtW+KqX4nYmbgXCh999DGkbHUsoA6bh5nhJlqWgAd0ZExvkymHYl6cQH7BjmGClLLWhA1Xn32yZZ7YUqtJFO6Z9QKeUZRMEnywwEEtRabJDDhkAAAgAElEQVQZEJSidciwkUVONww+J0kVlIVU2F2NhdVG6yxEWRI5YLploMaeljIhGaEdT6vu+y6xnuF3B0zHtdXl1OFrOIHD3/3aQmfIiKJXz33yyaeK9vxcuITbKXKcAcGWQXo8PD/h95B4BQSZPQRVkl2Eth1Xv4CYViwt+IoGFeF205aqiXNFtR0O00zBj6u0+erk6bOLnE4L2iCd3ZKTkzFo0CAw+qp3FQ6BuBcKjVudhTOrWNvhcIwj84QlEZmYEh72yWL/nCdoX886DA23SrKX52dra87JRnv7sKsr9i9T63Vb1XTph1+vADkxb9iytXBvr5BPpTU/E21p/eMkZDMFr0zXzOv4GUIwLuZ7lqB9XUvNEUpXbcrZ7+mCH1YJKpUR7Db6dPv/zWdimq7PH7qmWcLDgQ6et86Kdt5RdKEz6H3dtHVHdK/vTqe0MuI7f4iWRE70ly44r6FgTucwO16Dj/1OXKwD5z2hVJ2mLIVFuqBxVUEPWizx93CY+vVZGfu8c1f8h4z/4IMPkJaWhpSUFHxseXUXcpr8YR+La6GQlXsVKorgW9p0h1vNkJh9grqVBLM7ujBils3Uk/Ix2tQ7TUozgczdUiGN/JNLGz7BL2sEKckCOhmFXQmy3mzB3pHsT2kceqNovEuXrrwS1UX7XoRcSZrxBrQpLnXQjitflg9oTEPqsk19oe55gv7NBcNbuTA+vnvrva2/yB3TfWMEUrIyyCCK4lq1NlPRqaLRUKtzM/Yc7RMzg3SaH2aHwLI2FafyMQhH+6Ze+z1PcOFpgmm0ZHKibxum1w1w2Fmz7mzBX4bpd/zZ/31eFJCedBtr165Vwnfjxo0nXdcfrYK4FQrc/iWlNMCfSbBOq8+A4O5RmmDpDOXI6DL0qqdiGcGHVO84TWD7ROPngODqvto+P6yAMs9kCzb3F5RIsqyknNrJFTQpL5gxd3HMae/bb48iOaUWNpKxhlMFWUxgq2W3rsxCnfqfoc8RuJJ8f37hMKXHOPXXYVerVp+utcxhHVe2LJsjSE0WTJwae5XHjz/9rMKfbLvYXVjtGKrp9EueI7hgStUSMf02nBrI0FrwPUuQ3VNwBi27nNrgc1kC+u6wHSWkwu0WrN8blBLMmhd7Oo3WRLjtttvU2MaOHRutKv8Q9cStUJi9YAkqk1idBEK6ZiY8jAv0iGBFm6XLpaa41Bs80fg9QzvJlSxhOcs5TThrR0IfBh7SOqqzMgXG7PCdd9+PKdHNnrcQten56rJK/WaF9hW4YaCL8CAuAe1t25LqMo47HGMJg+khi/nRnNWRiaVr/XaDytqCxpEu/IL9l2tm9/U3sfV8nTpjDhqXt1bl4cbu0/4ujAir1JtOApk40QfjQu3M5yosg3HlwsdS+7kKT6u/dETk+YXjzsIvOKAwTcKbbyWO0xg9n1u1aoUqVargww8/jOn8OlUqj1uhwNXL7pEuhBoQ0FmHK3KaJToyFWuyDW+pY/O4qkSCJxu/52pG8zi9dd2sQfy6bxyH68T2CXo1EPQdGDvLmR+OHVOrpgeczkQ4xoDg+IqcKoZwjM7gkyu44DTB2DYuws+Ut99Zd7rG9GV6ULupSQKCO0cIuNNTKkUnwRwQ9KgnGDb68pjNVTIZBvB7jg5/Tqoav+CaftphLyK6yxX0amKpgNwEiB1PfvYJPlmkMXX1wWH5LMFdI/UcUo5tTpjmClpWElw2YWrMMI1VxfPnz1f0v3nz5lg1ccrUG5dC4c/bd6Kq0Xs7MaVcfQC5gL4LTjsKEr9VDw9Ec3u7bPWDJ5r5vk572t5E7+ZwViOmrMXwGCLjRq64ncr7BWTW5StXwdfffBsT4tp6607UK6FjDhks1ErS9Nfc12kvbcYycuyzKZ+jQ1bQFNhRJWXK2+/EyCeoX0kze0fGap7L1gzvZjd1jV/w93GCMtUa4tNPP40JpjfevE3RqRJmTnSaqTGlybIrnXKc+YIq5QTX9I/wHRhseE/XKieGdrn/EhdhZZ6zFjv3ui0YuAMbKyhRqS6++fabmGAay0rvvvtuZZ00ceJE0L/Bu0IjEJdCoe/FwzGsaRhba0PIlkUQHaoiWrmn6xg9DN6mHKbcVvqmHfs9V1su0Rs3IgaWKxh8umAQneSchILFUEowic+9sYnl061HP4zjgW4E/eDu5nEexLthlC44tlLHllLxo5xWy3Yc7Z8zdNyeNedHKFRydVBCRrd17Z9lifPUU/8ITf0n+Wvn8/tgKp31nMadrv1SiOmr9M522w0Rm2wBVaLcFTnWbcfRfLZoiRFpIxbU2YI+TTWtOu5k0gXfrdBCmVF0E/H6/PPPkZqaqjK7ebGTQr/BuBMKPGCuXK8FHqfJnhNTsiJKcrI5MjozWXwCOuswdIKyuY9kcppnzT1HMOh0wTgyAifmaspnCh67XFsiuR4u5gk6MsbNnIWh39RJ/PrzL78ipVoN7HFTx/kFXIHXrmAFpHNa/XKMPsE78zSmvLuq7wwu9rtfq57oyObIkMwzmYKHLxMwrMjPNCxw6mOu4OxqscGUr4O0xzDrjozbL9g+VMcdUvG3nPprYXpkqd6R/jOUZ7LBwemeLRh9hmBoywgx9Z8w1gjp9GZvyyfoVluweGX6SVBk8T7KhENz585VEVd5GO1dv0Ug7oTC3554Qk02x4lGIvULxrcVXOS2ozAEbbOSgZuli3km+G5ZdqiYPU4CyzxHBmCZUj5FvbPTM37B7YMF9Zq2UdnMfvuaTu7b3nvvV7kjXMedKxh1hjYTdWUOHGOG4N/T9Mrx2GoXBm0wCb4HBBkXCJqbqKnB/w/+bjPXfMMtbpVfcGM/QYWaDU8OwBBPH/j7P5QhBENLOArDHMFFTQSXcSERyflAhuC5Kdp/gxF+HesOxsZ8zxbM6aRzLTgaOZjyGQJ64VPIhXV6M2WzBOt6CipUrRUClcT6aedOHZLkkksuSayOx7i3cScU7tl7nxYKoWIWGcLk3acPONMZYybCycaQ1yR8FZbZbcVmb8t8ztIhAs6q68LgTXneLRv+Ry5zeSZD8CYtcUqkqJSU0XzvjMdD7+mwUTZNf9MFbWoLNjBMQ4Q7ob9aVj6M/xTyjMLUHe6epdvj7sTRKso8n64D5rE8vXcdBW2m4MA4/c6jiSfr2njtjTiNVkduOOVrJzFlHRcJnbLPV2ihwAi9hRIKAcFVfQR1K0aOKSPX8mznHidHQr4DLl6GCZJKlok2pMVS33/+8x80adIEzZo1wyeffFIsfYi3RuNOKGy+/iY0KuOy7U3XsW4apghuGeKyfTfMJEPwtBVRU6kcCiMUGCJjqHaUc2RGpk3eA4IO9QSr3eI2+QTvWau1b6J82LxiTaYKi+24+qfue40OJ85EL647NY4tU3DSQoEM7CKdqCdSofDrldpckyGnHZkyo+Gadx7lmefzZ4PZ6BwxJUZ0rKwouHVo5Jg+MUELBVeVo53O7J8DgvV9CoYpBTo9nG91m08Zgn9NFlRILoGvokynUX5FBapu6tSpasHoZXYD4k4ozF+6Cl1o8+4UPyZdW9HQa/hvV7isFs1kyRRQR6vOICgQCiMUMk+Ev45YKPgFXVMFS3g47bRS9Ak+s0wJPz8S3bgti5Zfqc4rHFUJ1sF95TJWti8nVZcN02gIBVrZMNNYREKBbadrr91FXVwwzdBxsPjOP/viywIxCbfCo8ZOADPTudEpTaWrlxM85LZTtGFKocCMdgwDUig6LahQYNs5gk4NBIvpwe5Epxk6s2D5Mkn48KOP3WBKqP9v375d8Yfp06cnVL+j3dm4EwpMDj+5tQthpmu/BE52FT0zkkPjKAkFppxUgiUSpsnJFhAwrAFDD7gxZWaFKyOCF185GNX33H/oGMygTtvJbJf27YsFZUvqzGoRWclEY6dgpUpVmIZLImMYprlnCa5oJ+jH8ySnxYNPByakVdfb7/0nqpj2GzJa5QF3a//N2To8tgrSGAmdBgQb+wiqlrNCxJsxF+ReGKFAf5NGlrOlE51Ycy+ljODR/Qeiimk8VHbkyBE0b94cNWrUwEsvvRQPXSryPsSdUBgxdgJGNnNhYIkmFM4W9IhAKNDqhMzx9Tei6zFKoTA9EqGwSAsF1yQ5hkFFSSgwX0KBhEJAcPmZAuZ0dmPKjFZLoXA4yt7ifQePwjg36x6f4MOFWhWk8lBEKBToB8Psc65nQOY9BN8LKRSYYnYWM7xFKBT+egoKBXJg5v4eOZKpaQX79+8vcqZc3A3GnVBYEKH66OfVelvuGLXUPlmitFMw2dMKoj5iMhU/wwg4bcstk1kS4udRVnWsycxFO0aaZVRUOyb2z5ZVD9UWBVHJRUN9xLSpPOQskPqokWBRBKqONy3jgp9/je5UmzxjLgYws5rTTsVavDAV5oNuJtbmXWQKaKnG0O7KS78was7CCIVsffa14jwXOqXF2RSeKZQ8pc4UQlHHvn37lGAYMmRIqH+fsr/FnVC4ces2VKOljBMDsw5F0yoX4AAvQ+vK1Yq0sGcKfp2KUqXmdHJYMhOcd+ugmQnuHQ9FGVtJMbASYOC6aF5rM7K1UHCy6LIwZT5gFfPIzaqGY4vGToEMrIAHzT+tFjSrJmDQPkdMmQfDCqUdTTxZ19rMbDSLxGIqoM9Lthbg8D5qB82R9I/v0Xr3NNxwPRDPELyghEIJfPV1bLzvo/2uTqa+l19+GfXq1UObNm3w9ddfn0xVCfNs3AmF3ZGapGYIBrfQ+ZMdt7uGQVsB7SgUuMso1AFeloAmsO0KYZLq6nWdIXiNNv/J1fHDDz9ElYB23n6nVs84BcIjTj4BzW0ZZdNxV2MwtQuFSM8DzLPmniW4uo8O0x3RTsEySWX4kEhMUvdfZqmmoooosG3H7WhEvb/b4iBf5/fOjDQMiGWSygN/njEV1iR13UVWRF+nhYB5BwUx8/ULbh1M0+nSUUY0vqu7/PLL1Ry6666iy9NRXIjEnVD4+9+f1AyMk81p6+wXXNFWcE5qBGaBJH678xq/O9VtJkvwPUuQ08tKOB/JQTPbyNBM6dnJLiEOeMDYU9Cq/blRp4VHHn0MpZK0fb/juHO0JywD3EXEoG0ROVVWtMJg6tf5rZn4yHF3aN6FzXnN1cggIFjXQ1CrUcuoY/rs8/9GeRH81y0Ee46gbzPBJW7GE2Z8XBzM1NnTVC4FpwB15pnge7Y+MOYZQUSYZpxIUsUIuY6CiBFcuwtqNmgcdUzjvcJdu3Yp3sTYSafyFXdCgavk2o1b4w43e2m/YB+Dc1HVxAM8N4ZEk8vFOsnJC9NcGHTwJDPfcwT9mgkmtXNRW5jyVqTUepWsvApOfcwXnF5JsHDpqpjQW43a9bE1Art+HvpylRqRjbxP8NEiQYUyApUTO5KDVIONufsFjGOkmKaTft5Wnr4iNctrXxXH954jaJgsWL46NiEZuOvc5eZ/kCmgxRoxOuLm/cwxWjG6GNPryQkRmlsbbMzdLxjYXDDxLJdDY1M+oNWiSrXqtJu06Ld1JUFW/tUxodN4r/Szzz5DixYt0LBhQxw8GF0rwXgZe9wJBQIzaPgl6NfQ5RDPp6NBMkY9GZnrNt7aIjesIrijMIHGOIHyBM2q61j3jrpsM9nydPC2YbRScbHoYHhtTsqHHnk0JrTRd9BwXMaE7k5nBZz0VhA513SRHCNTaq7Uqh/XCJsGk+B7huDs+lotF5HKKk+nqRxPayon1Y1tLE8//UxMMO05YDgmnhFBP3y23WIkO8wcQekShaRTjjtd76Aj9vbPETCA3lRma3OiU5/ebZJOD735VkwwTZRK+/fvr+brqWidFJdC4YmnnkZZiWC1mifo3kgwmSsiJ8sew4jSdUROV0sgUz74vk7HxFcev07Mlc9ZQos5iF0tpLhSGyioWqtuzObEQ399XPlAuOYhyBN0qi+Y28lFgBhsGL68ZgQe26a8/U4G5hNUThY45hQ2z7C8pY5zDQsd0LGkqqe1xHfffRcTXPfc94BWdVLFw76ZfgbfA4LzGwqmd3BZ6Jjn8gVMBMWsaBHRtXmO93TB18u0SSstwyKykrPCkbueewUEO2gum9YS0T73iskLinGl992nQ/KMGzcuxi0VbfVxKRQIAVcjN7jFk/cL7hmtV2FfuaU45ITJEjAa56AWEepa7ZONn3N0WwciSbIT0HkU1Jacq8NwTMNijJ1rCEZeOj6mb19KlscOWsE4CVC/YNdwPc5fGTjQTaedo3dDY7hidrIYC8aS3zn2giTZydLhG8qWcvH2tTBtkyKYPH1OzDClKqFkpdq4gyokF0xp0aVowe2szKIzBnpkwEfH3VAoTH0CZrFjWxGlnM0W3DBAC2a1YAhHp2wrS9CkomDBkpUxwzTRKn7++edRu3ZttG/fHgzLfSpccSsU1l29WZ8XRMBQGbVU6U/dmFJAwCTlzKngqEYJNdkyBM9P0TsFOkQ5MktrYnFiMq+z45Y8ICqkNct+/8OxmNJU3roNmjG5YMqQ1E2rW96tbnr+gIDOVk2qRaDjD8aVcXSmCEqXFHzupm9nSstlgkrJguu4WHBiwgHBXZZgiymgAFauyUDVpBMCLuRugfSwRkAT6lVMXuTUd2IU0GbBLaoXInijPd4T63Ji8j7B50s1TW9h4iinfgUENw8QJJWpELNEULF+V7Gsf8yYMWpu7d69O5bNFEndcSsUmBmpWurpWMX4Nk7M3i/YM0avjL5Y6nKAnKFzKZQrrWPiODL2YAZmWR4xaJjj5OFzuYK83nr15Rq/Jk9QQQRLVlwZ8xf+3fffo2rtVOTTZ8JJdxzQOQsoqHiQrA7yg/Ew330ChnhmWRXKwW1nYZ7jPUvA5Drt6kSQsjRXsPw8K6Wl02qbTDBbUFpE+RLEHFQApcpVRq6byWlAwB2mwpT5qJ0O5TMEr8/SZQscKTVLCx6e07jSd7aA8aMoaB3nGDFNF9QQwer0QFFAmpBtbNmyRb3fOXNitzstCmDiVihw8Dt23YmSIvjPfBfdaLagS6q2DHK1RLJCWbuGCLYzL34O6PMLmsE6erFmCmhKmJSkk6s47kioDmFs+ur1EO3IqOGIZ+ftdynCfZ9JcZwOPXN1ms2BVLU5MWFiY6nVaGXjWGcwplZ+50luVjIZAiaoIUO9bbiLSiVbkNVdUKZKfVC9UxTXpmuvV31TOY6dMM0WNK0mGMqEQk4LHe6KluvxRhxyxGCbL2hdW7CQKWqdDuIzBcwFQUypgnWk01zBqq6C8lXr4piXxtKRpN555x2V2a1t27b4+OPEDBgY10KB6Hfr1R81S+jtd9iVT4bg08WawBdyZ+HkSJWnBYjKnuY0acwk492KYcMJ9JJTgnmf4H9rdeaynoyg6bQaz9Z5mVnnvodjY3EUjno7d+uJBgxPztVquJW9LcKoSpXpxMSydEIXBqlzFJh2TJlLeIWgUmnBfU65gX3anJehIkYwBaeLiuORsZoOHiviuDxdL+yLloz0ylV1OEwzBQyQx3e+kWpFJ2MFK1/INMYiclPhGVyttlm/cuwLR98UsisENcsJLm3jsmsJCB61MI2VZVw4Ok3k3xkag+9h7969CTeMuBcKR48eRcPmZ+o4M2QIJHwzCez3gDZN5Yu4lyufcAzZL9g9Wvsr0Aw0bH32uv0n1Clh62W/sgX9mwkaVLYOQsMxB/+JleCqNb4iJxpa49Q97XQdeNBpF+AXPGol0bmbyVccMKXvALHH+jDvx44nP/t1DmL1TDg/E2KaL+iaJqhPhsvnHDClHwrrS8/MKnJMf/n1V1SuVgej3XZW/hNqpH00pQ6HqRW/qEKpAggFWlwNF1R1CrtN/PzaZLUR42Hx/YfDNCBgdjtimrtuQ5FjmugN3nLLLQq75cuXJ9RQ4l4oEE3qwiU5BZfSzp6CIRwRZ+scwyRileks1OrWJzDRSJWXsdN23zCyPMH5pwmUmiPUSpXMy69NDnlo+hkPTcPVG9DWITS5vWT85GIjFsZXEknGNKrDnDDN10lwiKlSD4XB9P35mnkoJ7ZwYzd4WkKBVmBD6MMRpk5iyB0drY34zsJi6te5KCqJYOyEqcWG6Yf//QgiFbDArO7D0Wm+IL+3xuv1mWF2P1Z+i5IltBBRzNuOX6jPfgF3qGpHFQ5TRgJoJyo9q3JQDHe24deH/8nFjGmxvcwoNXzo0CFUrFgRLVu2BPPPJ8KVEEKBQD773POQEuVwSXNLKIRjPDmC8e30hHuQKzFOjuDdRabORazCADh5cHLi8VnrHOLRUIlSOKlyNXMj41QRRkMJDtaVJXhvnu5b+3O6FTt9/PWx/RBJwmVkzBxHOAaRKZjcXvdbOalxdRuMaZagR2NB7yYRrGx92geFeNGi63fM3sKUDI5liNnvyhimSEytjHWt251d7Jg+fuBvqs/jqepywZSHvBwfd65qxxCMqZXfeTjPIMLRu8GB6VytiLCvhVJx8vlMndeDbfIgO2yd2YIXpwooEM7p1qPYMU30Dvzyyy8YNWoUypQpg0ceeSTuh5MwQoFIfnHkSxXHJi1Z8CmtYsJtvfO0NyiJ/7iXpp3hZQg+smy5VSiBcLpXTrhsvUOgx+fvVmvZetVPdRGdjWgfHlLnzRVjroBOb+zTgiXL4oYweMBdOqUeGiRrHX9ITMms8nRUUvZfHWIS+yBM6SvC//97qgPDIab5Woiem2YJeDszzBZ8tEDA0CA8lFW7rlC6d2KaI7hlkG5z6cq1cYPpl199hXLVU9G0ooVpqP4Th/U6QiwxU0EIWS4IU7OIOEQmbv+fEQbmniegrwiz/P3uHQZ0sqEa5QT06P+Su65QfSKmWYLdIzWmU2YkthVN3BCE1ZFNmzap+bFsWfzM/1AYJZRQ4AC4BTujfRfl8aychngIF0ovniugzpYT7tyGgk8oRLhrMBMrT3BmbcFFXNlygtgZk5lomfo51vHPibZ22F6u1okz9hKT3avY98HChZPMElwz2uq+rFwdP8zLEMSXX36pMC0ngu20V7/KNlaDBe9Zgr2WsyB3BLRxVzmKDabrdJTVAdzNhTvst1m93DnS1o6F6e5RGif6nqgzn+AVssHUJxjfSpfNzl1nhhI3d9Jp6/adla/NblpMbbCN1Y6pX/DUBD0Oej0rCyZGNiWmpEmfoH1dHcso7HlNpuDH1boOtTs284H3fMHOYfp/HetZfg/mfZl+WAKWO4eBp+myt2zbHjdYnkodee+991C2bFnQOiler4QTCgbI627cCildHZV5fjDWcpyigLATfJaeLEyFScbOGEQqAxYZdc6JOC5MHK8EhpkkvFvMh8lfmCQHGy21iE8nq2cyGtaZZ55lefM8J2OOFig5F+hyTVqdhXfee990Py7vazOyIJXqo04pzfyVeiEEpvS96NtUj2vknwSH51jCL/eEFdgt9JwO1msTI5+AB5xDqbKi8MnW7+7hywQMAkdMeViqLG6CMc3WB/RLOulyrTt2w+uH3oxLLE2n1vgyIZXrIUUED1OdSfokpvaxBXQ49/7N9bhGnSE4PNfadeZqz2Tiopz2gnfHVj21K1oe0BQorD9dhw7hc8kltXe9eh+mXQoci04Z4Xa2pR7s0LUHDr5+yHTfu8cIgREjRihav+eee2LUQuGrTVihwCF/+umnWLpyjQK3URnB8s6CFyZZqzIyJE4O3tfpcMRt6whKJAloe8/VEyemybmsYulwQvE8gM8FBFPaa/NSfn9rtmB1N51LgRNt5XmCY8zLQGsb0w7PJwKCe0cIxlgTPKlsCu67/wH8+muUU38V/p07PslEIpeOm6Qw/VNFwcIOgrdnW6G07ZjmC6i7ZshrBm/jgfG19DTOEzw9STM3tWol4zeY5gpGtxYYB0CqRujh26qmLh/ooZm+WlXbMc0S7BkhGNZUO6VVqpmK23be7jiOePrnJ598gglTZylM21QSLOgg+Ii+N9xN2THNE/xrqvYzKJmkw7HcZoXQMHSqAhVy18HdLTFaJ+DZGIUCaZGhLZZ00btg0mnGhZYlHJ+hQGF7pFO/YO8IQd80AQ/opUJN3H77HfEE2ynfl40bNyqauOqqq+JqrAktFAyStE7K37AZLdt2gpSroYA+t5bg4kaC5R0F1/YW3D1McE0vwbAmmgFxwvCvWXlBmrXqvzBVcF1fwTJ6eSbp//egILHKsnzVEoIlZwtu7CO4fYjA300w40xBn1TBnyroZ6rVb4pe/S7G/fvi/1DJYBh8/+nnX7A63Y+2Hc+FlKmmsOpRVzC0sWDVOYLrLhLcPVTngBhk7cQMpqeVFZWAht/7NxbcNECw7Bx9cMnfOlX/7TuoWUqwopPgpr6C+0YK1nYVzGkn6F1fcEZFXbZK3ca4aOAQ7HvkseCuJtT3RctXoU2HrpAyVRWmfRsIBqQJfF0Fm3sLqGq6/iJBrwa/xei0ZFG+JcTvglTBzQMFK7qcwLRnvd+W5w56bRfBdb0F+0ZrTBecJehVX0Bhz3oq1kzD4BGX4s67E8+WPqFeukNn6eDGd9GkSZO4yex2SggFO+Zvv/02tu3YiflLVmLc5Jk454K+aNq6I2o1aoW2nc/H8DGXY9GSpaBL+p69e7Hp2hsxf+ESTJw4CU1Obw2Rksr8tWu3CzB79hwsXr4a22/bhd279yDd58PM2XNxYd+LVTKcag2ao02n89F70AhMnjkfazKy8dj+x5UJrb1Pif75jTfexB133Y1Z85fiimlz0Kl7HzQ5oyPSTj9LYXrZhClYuGgxrr/+euzdey9uvHkbZs9dgPHjxqF+o+aK6JMr10LnLudi7tx5CtNbd+wEt84ZGRmYu2ARuvcagDPO7oaKtU5Duy4Xov/QSzBl1gIE8jbgwIG/4ZtvT63Uj4cOvYG779mDWQuWYfq8JWrMjVq1R53GrRWmY6+YjNlz5mHr1q24557d2HjNDZg1Zz7GjR+P1MYtFKalK9VEm3btsXjJUrVjvvOuvyhM/f6AxrT3QI/jw4EAAAVFSURBVLTr0gMpdZuq+vsOGX0c08cff/yUCeCW6POLfkNUJ9F09cknnyz24ZxyQqHYEfU64CHgIeAhUAgE1q1bp4T9ypXFG4XWEwqFeHneIx4CHgIeArFA4I033kC1atVw3nnngdEciuPyhEJxoO616SHgIeAhEAaBY8eOoU+fPmrX8NhjRX+G5gmFMC/G+9lDwEPAQ6A4EbjmmmuUYMjOzi7SbhSJUPjggw/U4Oju7V0eAh4CHgIeApEh8MILL6BcuXLo2LEjjhw5EtlDJ1kq5kLhf//7HwKBgBIK+/btO8nueo97CHgIeAj8sRD46aefMHjwYFSvXh2PPvoorr32WsybNw+0IIvFFXOhwKTWtMPlX4kSJeAJhli8Rq9ODwEPgVMdATq5GV5q7txJRPuKqVCgY0bVqtpJxwyidOnSKoxsixYt4P15GHg04NGARwPuNMDQ2x06dPidUJg0aVK0ZQJiKhQYFKxp06a/GUivXr2UQw63QDxI8f48DDwa8GjAowFnGrjuuuuwefNmcFFtFti8+/3+xBIK7C1NqurWrasGQttbxtbxLg8BDwEPAQ+BgiPAbG41a9ZEUlISzj47NvlDYrpTMENmQLCDBw/ihx9+MD95dw8BDwEPAQ+BQiBAtfzrr7+On3/+uRBPuz9SJELBvRteCQ8BDwEPAQ+BeEAgakLhpZdewhNPPBEPY/L64CHgIeAh8IdF4N1338WOHTuwbds27Nq1C1988UWBsIiKUGDmruTkZDRo0CBh8gYUCCWv8B8GAUbZ5QHe+vXr/zBj9gZ6aiHQt29fpKWlYebMmWjfvr2i5xtuuCHiQUZFKPAEvF+/fupAuaBSKeKeegU9BIoAAZr91apVS4UBL4LmvCY8BKKKAB3dGjVqhAMHDhyvl87DVapUOf7d7UNUhAJXVgzixDuj/HmXh0AiIjB+/HhMnToV06dPx9VXX52IQ/D6/AdHgDmgyYft16JFi9CpUyf7T46ff/u0Y9HQ/5w2bRqGDBmi/pmSkhIXSSJC99T71UMgPAJPP/20WmGxxMiRI7Fhw4bwhb3/eAjEKQLPPfecEgoPP/ww7r//fhUOo1mzZnj55Zcj7vFJCYXXXntNdeD993VCem5R7rrrrogb9wp6CMQDAsyfXbt2bTz77LOqO0OHDvWEQjy8GK8PBUZg9erVipYZXoh+DFyoP/JIwdICn5RQYAo5blU4oUw4i02bNhV4IN4DHgLFiQDpOD8//3gXxowZo9K1Hv/B++AhkCAIdO7cGbm5ucd7u3//fsWjvy1AOttCC4XDhw+rxng3TmmMwxGLWBzHR+h98BCIMgKGjnmeQNqdPHkyUlNT0a5dO3WuwF2Ed3kIJAoCZcuWxUMPPXS8uxQGXLgXxACo0EKBk2b58uXHG+cH6mEZ99u7PAQSBQHG51q6dClWrFih6Jnbb+pgu3fvju3bt4Oh373LQyAREKDlUcmSJfH9998f7+7ixYtRvnx58H+RXoUSCjzAoF9C8PXAAw8oNVLw7953D4FEQoBnCgzQ5l0eAomEwIMPPqh2BTVq1ID5a9y4MWhEUZCrUEKBW27G3gi+uFV55plngn/2vnsIJBQC69atAxc43uUhkEgIMCbSk08+iaeeekpFl3jllVcK1f1CCYVCteQ95CHgIeAh4CEQ9wh4QiHuX5HXQQ8BDwEPgaJDwBMKRYe115KHgIeAh0DcI+AJhbh/RV4HPQQ8BDwEig4BTygUHdZeSx4CHgIeAnGPgCcU4v4VeR30EPAQ8BAoOgQ8oVB0WHsteQh4CHgIxD0C/w8JutrJZnt7rQAAAABJRU5ErkJggg==[/img][br]Write at least 3 equivalent ratios or equations using lengths from both the diagram and the full-size garden.
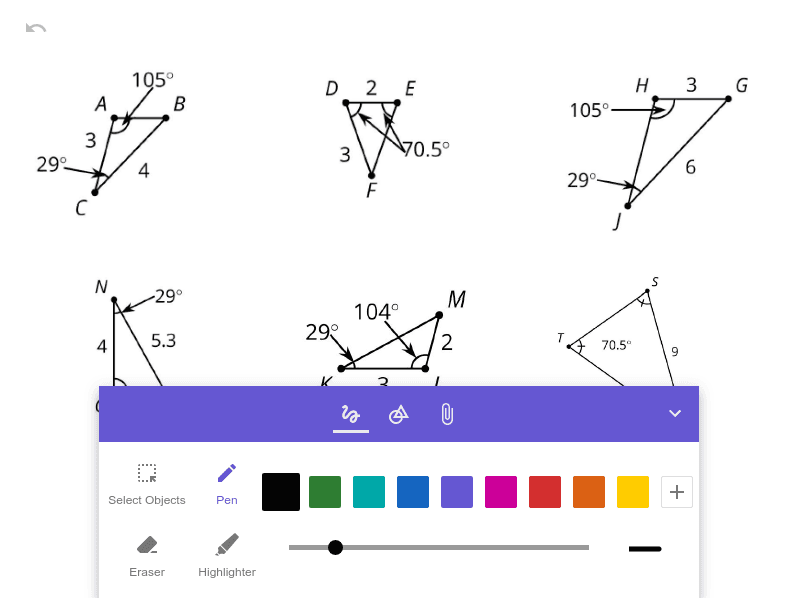
Here is a set of cards. Group them into pairs of similar figures.
For each pair, determine:
a similarity statement[br]
the scale factor between the similar figures[br]
the missing lengths[br]
Here is a quilt design made of right isosceles triangles. The smallest squares in the center have an area of 1 square unit.
Find the dimensions of the triangles.
Are the triangles similar? If so, what are the scale factors?[br]
This quilt is meant for a baby (1 unit = 6 inches). To make a quilt for a queen-size bed, it needs to be 90 inches wide. [br]What dimensions should the center squares of the big quilt have to reach that width?[br]
Here is a quilt design made of right triangles. Find as many different size triangles as you can.
Write similarity statements for 2 pairs of triangles.[br]
The smallest triangles have legs 2 units and 3 units long. Write some equivalent ratios or equations that will help you determine the dimensions of triangle [math]LCQ[/math]. Use your equivalent ratios or equations to find the dimensions of triangle [math]LCQ[/math].[br]
IM Geo.3.12 Practice: Practice With Proportional Relationships
Quadrilateral [math]ABCD[/math] is similar to quadrilateral [math]A'B'C'D'[/math]. Select [b]all[/b] statements that must be true.
Lines BC and DE are both vertical.
What is the length of [math]AD[/math]?
The quilt is made of squares with diagonals. Side length AB is 2.
What is the length of [math]BD[/math]?[br]
What is the area of triangle [math]AEH[/math]? [br]
Segment A'B' is parallel to segment AB.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARgAAADRCAYAAAAXHq1EAAAgAElEQVR4Ae2dCbQU1fHGg7LKougTZAdBY3BBQAVlkUVBAWWPIMiOooJEARGMgCgIuAQQg0BEkFUWMcqiIg81sgkoIJCAQQmyBAmSGKMYjfd/fvW3n/O2mZ6Z7pleqs6Z8+bN9HT3/W731/fWrfrqF0ZNEVAEFAGXEPiFS/vV3SoCioAiYJRg9CJQBBQB1xBQgnENWt2xIqAIKMHoNaAIKAKuIeAowQwYMMDccMMN8mrTpo157bXXXDtx3bEioAh4HwFHCeYXv/iFefnll826devMgw8+aPh/2rRp3kdBz1ARUARcQcAxgtmyZYsQSuRZdujQwbRv3z7yI32vCCgCIULAMYIZP368ueqqq7Kg+/rrr83ll19uJk6cmPWZvlEEFIFwIeAYwTRt2tRUrFjRjBw50gwePNjgj2Ga9M9//jNciGprFQFFIAsBxwimePHiplOnTkIuXbt2NdWrVzcrV67MOpC+UQQUgfAh4AjB/O1vf8vlf3nmmWdkyvTFF1+ED1VtsSKgCAgCjhDMokWLTEZGRjZIWU2qUqWKOXz4cLbP9R9FQBEIDwKOEEy3bt1Ms2bNBLV///vfZv/+/RIL069fP/Pdd9+FB01tqSKgCGRDwBGCYSm6Xr165oEHHjC9evUyF198sWndurU5evRotoPpP4qAIhAuBBwhmA8//NCsXbvWrFmzxqxevdrs2LEjXChqaxUBRSBPBBwhmDz3rB8qAopA6BGwTTDHjx838+bNMxs3bgw9aAqAIqAI2EPAFsG899575sILL5SlaPKLiNpVUwQUAUUgFgIxCYZVIALnIBbrVbBgQfPpp5/G2rd+rwgoAiFHICbBfPPNN7kIBqIpVaqUueOOO8zSpUvNRx99JPEuP/74Y8jh1OYrAopAJAIxCYaNFy5cKIRijWBatmxphg0bZm688UYJsOPzGjVqmEGDBpnZs2eb9evXG3w2aoqAIhBuBGwRzOnTp01mZqbp27evTJOef/75LNQ+/vhjcf6OGzfONG/e3JCTVKRIEVOnTh0Z4UyaNMls2rQpa3t9owgoAuFBwBbBRMLBaKVhw4aRH2W9P3XqlNm1a5fEwkA4BN+xPT6bmjVrmltvvdVMnz7dkLukpggoAsFHIG6CYTWpRIkSxo6/5T//+Y/5+9//brZu3WoGDhyYNZ2CdIoVKybZ12+++WbwUdYWKgIhRSBugnn33XdlVJLMUjXL3tZ0C7LhVbJkSXPXXXeZDz74wBZ5hbS/tNmKgK8QiJtgaB2E0KJFC0caivLdSy+9ZG6++WZz7rnnyr7Z/69+9Svz+OOPG6Q4mVJ99dVXjhzPTzvZvn27jP4YATL1ZESIHTp0yLRq1cqsWrXKT83Rcw0hAgkRzPXXX2/Kly9v9u3b5zhke/bsMVOnTjWsVOG3KVq0qDnrrLNMkyZNzJNPPmlef/11wzY4noNs5HNBtPi7atWqZUqXLi1TStrMKLJ+/foGn5eaIuBlBBIimA0bNsjF/9RTT7naNuQ2Wb2CWPr06SM3Gr6b8847z7Rt29aMGjXKLF682BWic7VhNnb+xBNPiJPc2nTv3r2COVNICPjRRx+1vtK/ioBnEUiIYL788ku52Hv27JnShiH/wNP7hRdeEFkIYm8KFChgypYta9AEHj58uKxgBUGDhikjjvFIY0TDkn///v3FeR75nb5XBLyIQEIE8/3338sNfv7554uPIB0N++9//ys3GeJW8+fPN507dzaFChUS4iMW55prrjGjR482SEn40YiUJoYIydE///nPssQPoWKIqaspAn5AICGCoWHov/BEJcPaS8YNyRQCHwXnZ70Y4RCD45cqB9Z5W3/vueceL8Gs56II2EIgYYLB0Xr22WcbpknffvutrYOlY6NPPvlEVqNYlbJuVgL/UNxj5EOczr/+9S/zww8/pOP08jzmq6++agoXLpz1HVNDlvERUldTBPyEQMIEQyN/85vfyE0L2fjBmNq99dZb5v777xcHKs5iSOeXv/ylQT+YnCucqOkWKienixrfkcZnrKSpKQJ+QiApgiGxkRuUpWM/GpITVESgUBx5VCy9MyqjIiUO1lmzZhlWzHBqp9IqV65sZsyYkXVInNZEUI8dOzbrM32jCPgBgaQIhpFLtWrVzC233GIYHfjZkKUgcXPZsmWyBEysD05spia1a9eWxM3f//73EvDmZjv/97//CWl3797dkM/FyKVu3bpStSHdIys32637DiYCSREMkHAjMIrxsh8mka5j1EIgIULmDz/8cJbTmJUqqibge6L2k9PBbpR9Ib7o2WefNdOmTTPEwzB1O3HiRCLN0N8oAmlFIGmCIScJglm3bl1aG+L2wRmhQaL4cMijIrKWdvMiDgd/1LZt29w+Dd2/IuArBJImGPJjiM+oUKGCrxru1MlSpoUoY4ts+MsIh1gVYnDItWLak9NYtWJaZicrPedv9X9FwC8IJE0wNJTER26ssNtf//pXgxgXujc4jMEEHw4rQk8//bRE4eJHQfGvTZs2pkyZMuJghoTUFIEgIuAIK8ydO1duJq8F3aWzwxiZENY/efJkyZtiVMMK1SWXXCIJnJEjHipiqikCQUTAEYIBGILXLr300iBi5EibGLm88847EoNDKkMkwRCPwxL0G2+8oVrGjqCtO/EKAo4RDLk/3DRBl1FItuOIabniiiuyEQxL/Yxw0DJmakVAHVMqv+ZRJYuR/j44CDhGMIgiQTAsq6pFR2Dz5s1SkQG8qlevLhuTroAkA0vTVGuwRjiMdsisJoP85MmT0Xes3yoCHkPAMYKhXdwU1157rcea6N3TIVsazJCgyMvIFCfY7sorr8wiHMS3evToYV577TVDzIyaIuBlBBwlGFTokBnYvXu3l9vsqXODYNAitmOkLZBHxXTqjDPOENLBaUymNfE5SIv6JVvcTnt1G/8j4CjBEPnKDTNmzBj/I5OiFlSpUiWhUd+RI0ckkvjuu++WKONzzjnHlCtXzjRq1MiMGDFCUh527typhJOiftTD5I2AowRDtCsE065du7yPpp/mQoClfTBDoiEZQxT8xRdfNPfdd5/o+EJcEA4O4yFDhoi0KMJVQTJrZY64IutFxQqmnKlOUA0Srk62xVGC4cS4wHmaMpxXi40ANwkE89hjj8Xe2OYWOIOpF/7KK6+Yhx56yFx11VWSzkDVBlb7SKBcsWKF70c3LPtzvTGKu/fee6Vd1EvHcf7222/bREs3cxMBxwmG4DJuGNTj1GIjgM/k6quvNo0bN3YtoZGnOdIUJG7ir7HEt1gWR5oCAXE/5lGRaoGCofXif0rgQKJEVaulHwHHCebAgQNSn/r2228PXIa1W93FSANSTmWVSyKNlyxZIlrGVGrg+Lyuu+46yeRG6c9vhk5zly5dzCOPPOK3Uw/s+TpOMCBFLAwXK0XT1GIjsHHjRsGLPKZ0GSMpfDjkSBGVTf+RR9WxY0cR3kJ6lG3yStxM1znnPC7TcnxPxBOpeQMBVwgG0SYuUNTi1GIjQDwLdZ5Ycj527FjsH6RgCx4OSHEQ9Gcp/ZEKcuedd5o5c+bIlIpz9VI2OP6Xrl27pgAdPYRdBFwhGKZJXIxkWWumsL2uoBICpExwndcMpzFVJCjlywiHOJyqVauKrnHv3r0NSn/43ohGTpcdPHjQZGRkpK2MTrra7fXjukIwNJqVCm6Y48ePex0DT5wfqx5UEiAHyevGdAkdHCpuMoXCUYzoFhHH3bp1M3/4wx9clxbNiRHKis2aNcv5sf6fZgRcIxieahDM0qVL09xE/xyegvYsJXvZz5ETTVZuiCDGj4TUJ3lTaBlDlhdccIFIi5LW4HZcCtfa+++/n/P09P80I+AawTA1ImsYv4KaPQSGDh0qpGxva29uZSn17dixQyK6I/OoCPwjLgcyctJQD2TapuY9BFwjGJpKOVeeLGr2EKCqAcmMqa75be/sktuKbPthw4aJih/XBC/iVUgrIbs8P2lRO0dlaoQPSM17CLh697OKxIWEQr6aPQTq1asXeFJGx5laWqz6VKpUSUi1YsWKUv4GRzIrWIcOHRLNYnuo6VZeRcBVgqHR6M6GVRA8kU4nSAxSdrocSiLnkqrfkH0/c+ZM06tXL6kBBelQi6p9+/ZmwoQJkilOJLLfa2+lCk8vHcd1grEEwXEGqsVGgJgYCCaI06TYrTcyVWK6Q9AhOUYNGzaU0r6U9+VaYuWKxEZdnbSDZvq3cZ1geDpxw5DvomYPAUrHsuyrZgwpC+RJkdZAQiNVLllpY2R80003iag69cTVvImA6wRDsyGYWrVqeRMBD54VsTBglp/SnQdPOSWnRNQw6QpMlxYvXiwxNwimgxUCXOQh4ffzSjR0SkDx+EFSQjCEwVNyVZXu7F8N3DQkjKrFRoAVqFmzZkmgHbjxgnj69esnIx+3Y3Bin2F4t0gJwVBpgE5H+EjNHgIXXnihxBHZ21q3ikQAYS2cw0ynyBQvUKCAZImjHUOeHFIO6UxriDzXoL9PCcEAIgTTvHnzoOPpWPuYAoDZggULHNtnGHdEPXHqTRHEiJwo/i30cHjPZ0hl7Nmzx/VI4zBiT5tTRjAjR46UeIfMzMywYh1Xuxn2QzAEp6k5h8Bnn30mpML1SFoDvsHLLrtMRjgIquNMZgSEtoxa8gikjGD+8pe/yA0zceLE5M86BHtgWonKHYF3uiTrTocT8MfohaA/pCnwFUI2lPglypi0Br4j6E8tMQRSRjB49kuUKCHBUxoTY6+z/vjHPwopL1++3N4PdKukECAGicRN0hoIeCQGh8UJRpLImhJlTFqDlzRwkmpwCn6cMoKhLTNmzJDOQqxZLTYCJAxycT/33HOxN9YtXEGAzHZI5YEHHpCIdPqDF9OryZMnp1yWwpVGJrhTBOuRZUFUnteAAQNyjfZSSjAUB6NzKIOqFhsBRnosVSPuROyHmjcQYGSJcl7p0qXleiZLnBicKVOmGB4KX331VeB9ONZgAT2g+fPny+Dh4YcfNmgFRVpKCYa5bJ06dcz111+vXvvIXojyHnlKSFn1jaOAlMavuKaJwWndurU8CCAbyifzYGCE8+GHH5qjR48GinBYlaOddrSeUkowXAfU/+GGycl0abxGPH1otFPwXVHHWs3bCLDyhOgVwlso7PEw5cX0AaU/RNgQJqcqp18NxzgyLCSm2rGUEwx1ayCYuXPn2jk/3cYY06lTJ1nZYOit5h8EyKNat26dyJUQVUzsDdPdiy66SKZYVHEgz8pPix6sBqNUaLcSacoJhuVXK0NWvfH2bhZWLyBlP12I9loWnq2QmsApun37dkO5YEYAEA39Wq1aNdO3b1/xZXh9ZI+PCYJB2N+OpZxgOKkePXoIsHZOULcxMo+nRhFVGdWCgQAPVx4YLIszdbrhhhvknoBwiDQmwJJFESRIvWT4m2rWrCmObDvnlRaCsSoZOlmP2U5j/bwN9Ym4+NSCjQBlcBmxWuV96XN8OORRrVq1ynz33XdpJZ2dO3dKQT7+2rG0XbHUTSIRTc0eAla1TPXD2MMrKFshrkUMDqVhcPZDPFSfIMqYUjekPqQycZMVMe7dgQMHSi11nL44rTmPvCxtBGMJgqsMYl7dkvszLiI0T9q1a5f7S/0kFAh8/vnn4qdhqowfE9IhY5zRLZHHEA5OWG56N40yNKyOMa0jf4ugw7Fjx+Z5yLQRzL59+2TIT9KZmj0EKAFCvSE1RQAfDtMUgtwIcONmh2wo30KVBW74lStXio/HDbRw8iLuxWowL3xJeVnaCIaT4WZh2U7NHgJUTGROrkp39vAK01aU92WFhyhjRjPIibLag7wo79EyJkUn1VPstBIM8R3cMIxm1OwhAF4dOnSwt7FuFVoESNy04nDQMq5evbrca9TduuWWW2TlKtp951QGf1oJht7nhkE9Xs0eAgyBUbtTUwTiRYDETWqKU4+K+44XIf/kVVHFgbQH4tQo/ct3Z555pq10gGjn4QmCQfNEzR4CXCB0PnWE1BSBZBBghGPF4BBnxZSKlV2LfPhbo0aNpGYYaScYypmwOkIClZo9BOj4Pn362NtYt1IEbCJAYiY+m0iC4X98O4la2gmGMhQ0CE+4mj0EWrZsKYLgTs2T7R1VtwoyAqQoDB48OBfBMH1Kpspo2gkGZ1RGRoZU7UOHVi02Aoz2IGVNGI2NlW4RHQHSFYioZ3pExPCaNWtk+ZkRMvK2xN4kY2knGE6etXxuGJ0m2etKym6AV37BTfb2oluFHQH0XCjJiwbx7NmzpaidhYlTibWeIBg0T7hhUMlSi40ApThIGCULN9pSY+w96RZhRIAHFNG33HOE/OOmcMs8QTAIgtevX18U9LXsp72uXrFihVwgDGnVFAE7CBw8eFBC+yEWQv2Rj3DbPEEwNJJlVxqOXoZabAQsj//o0aNjb6xbhBoBlqOnT58u+jMsOyPDmirzDMGgkKXTpPi6vXfv3qZ48eISsRnfL3XrMCCAhCfSKDhvL7nkEjNq1CjDokoqzTMEg1+hRYsWwrK6mmTvEpg6daqQMpUI1RSBSASYCZCDROUDUgUoMJcO8wzB0PghQ4bIDeN2unk6gHbjmLt375blReQW1RQBEMBhSzxLgQIFRAN47969hhSBdJmnCObll18WgtHysv9/OTB35snDRcLro48+ynWdtGnTRjDL9YV+EDoE8GOWKlVKlp2RakgnsVjge4pgOClqJuGLCbuRVk9SI1hEvnLiQu0dvs9PjyPn9vp/8BCgcoGVLT1hwgRPNdBzdzLlHZRgjEHfg3rI1EmOZjjtzjnnHNO4ceNom+l3AUSAES0F3rhfbrvtNk/WW/IcwTAVADBEjsNsJ06cEO8/eMQyyEVJORZKwfmeQLnf/va3ItaGEgESll41zxEMQKFRQRZnmA1xZUgDsW/UyKilw0pbXmalWjBUVgsuAoxWWTkkloVAueeeey7fa8IrKHiSYO666y65ucK8/MrFhDD6iBEj5IXIc6VKlfItvgYZocuqFkwEkLukogDTYXLQUhGF6wSSniQYGsYNgz8mzMaIhTo4VF6gAFfTpk3zlcusVauWKJGFGa8gtp2RbJcuXeR+QGLWbzFiniYYKsip/YwAsoY8wfKyzZs3y0VI8pqa/xFgBEvtIx60TIl27drly0Z5lmAmTZok4KKSHkYjzDunMaJDsDk/42JkuZLaOGr+RIARK6oClStXlihcvysMeJZguDy4YQYNGuTPKyXJs0bCgvIT5Gihwztu3DhTpkyZqE8y8OJFykWqy1Mk2dzQ/xxiyczMNM2bN5dAOao5UkbW7+ZZgiEKsUKFClLBzinxGz91FqMQYhx49erVSyovxBLksgiGvxRPV/MHAmTG08fly5eXEeq2bdv8ceI2ztKzBMO5L1y4UJ7IZISG1SgZa1cQKJJgeB9m3PxwvRDrhJ+FMiHEMi1btkwc+n44d7vn6GmCYZmaG+WZZ56x255Qb2cRDPko1nsVBvfmJUHeHQ57sp1nzZrlu9Uhu6h6mmBgeCIVUbtjuU4tOgKQCitv/OVpSKnZKlWqRP+RfptSBJgOWZHXQ4cOTemx03EwTxMMgHCjcMOoNGTsy6NgwYKG+Tu+q8iL97PPPov9Y93CVQTwqfXs2VOu5QYNGoTmgel5grGU7ojuVYuOgFWC9/777zdFihQx5KyopReBI0eOSOQtDtxLL7006VKs6W1N/Ef3PMHwRK5ataowP3NVtfwRsMLHX3zxRcGL8HK19CBAmMDy5ctFqhLZDWQUcNiHzTxPMFScQ1OUaRJTAL9GNKbywgIzAu66d++eysPqsX5CYP369ZIXxuoQkdX79+8PLTaeJxg6h8xRCIYXTwO12AhALuBFDpNaahBgOnTHHXeYwoULS90h0jfCbr4jGG6aX//612Hvt5jtZ2kfrMKckR4TJAc3GD9+vODN0nOsgEgHD+v5XfmCYMgURsSYG4ZcHP5q2dTo1xYjF5aoNWE0Ok7Jfoufhbwhrslp06Ylu7vA/d7zBIOTlxsFBa+SJUua4cOHm3/84x9S40X9MdGvR4uMo2+l38aLAGksONBvvfVWmQ4xog6jA9cObp4nGOQA27VrJ22xRjJWw7ygmm6dixf/WjFEOmR3rnd27NghjtuMjAxJKlVso2PreYJ57733zJIlS6QVjF4Yin766afRW6XfZiFw5plnSiR01gf6JiEEGDU/++yzUoeKVU1CJvKS1Eho5wH+kecJhiJsiO9YBsF069bN+lf/xkCgWbNmsrwfYzP9OgoCBHtSepVlZ+JZqFelZg8BzxNMzmaUKFFC82tyghLlf/xUkDIC0WrxIUA8ETKl4IdcJblxavEh4DuCseoxr1ixIr6WhnhrbhCEjNTsI2DV50JoW1Mu7OOWc0vfEQwN4Ibp0aNHzrbo//kg0KFDB1HD0+qP+QD008cImzHSw4HLCz0iteQQ8CXBEM1bt25djVK12feWrg46x2q5EaB6A/osyCgwBR81apT58ssvc2+on8SNgC8JhlUlRjELFiyIu8Fh/AFPZvK4kN9Uy44AeUP4V3DgIqewYcOG7Bvof0kh4EuCOXbsmBAMTxo1ewigD1O2bFlDPWM1Y7iGBg8eLKpyN954o6F6xY8//qjQOIyALwmGVPhGjRpJcXgSzNRiI0A8EaO+OXPmxN444FvMnj3bFC1aVCpl8j6MovKp6mJfEgzgEOHLDUOMglpsBA4cOCCOS4S7whoBzfSHeBauG0ucKy/kTp8+LX4YSvGSBgB2aokh4FuC2bJli1woLFur2UOA2krcXIS7h8kgCPKGaPtNN91kTp48mW/zt2/fLtsRzMm1NX36dKOj5HzhivmFbwmGYe1tt90mw1xdfo3Zz7KBlZsUlmqZ+FmoD8WSc+3atc2qVauiAsVq0tlnn20o0avmDAK+JRiaT8wCT6U9e/Y4g0bA94L492WXXWY6duxoqCQYVKOOFHlDaOAigE51hVOnTsVsLv4pS9AsMj0l5g91g3wR8DXB4LgsXry4asPk2725v0DCEVK2c8Pl/rX3P8EnxwLABRdcIKOXeOp0I5Z+5513SkWG9u3bm9atW8tDDJ+MWmII+JpgaHLbtm1FQV8zW+1dAGQBQzBr16619wOfbEUwYefOnWV1iL+bNm2K+8xbtmwp2CxevNjs3LlTgu8YBc2dOzfufekP/h8B3xPMgw8+KBeFdqg9BJgakV+D5EBQ7Mknn5RrgOlNLD9LtDa3atVKpo+R2zzxxBMSoEhohFr8CPieYMh4RQcV9TY1ewh07drV96TMUvv8+fOl7xmRUaolWbvvvvtM7969s+1m5syZInimqQPZYLH9j+8JhpY2bNjQ9zeM7R5zYENWkbgpmQr4zZgKZ2ZmioxCsWLFTP/+/Q1OXScMn165cuUkypf9saqEQ5xRclhjh5LFNRAEYym6a6F3+5fDeeedJ0Fn9n+R/i13794tgW84cBmx/ulPf3L8pPr06SNO4pEjR0pdKWQuOK5aYggEgmDw8vNExvOvZg8BsAIzPzyZUZAj74yERHxHjMDcCu8nH4nM6hEjRsgKksqz2rue8tsqEARD43DwESSlZg8BRJQgGOonednwrVx00UUSUIkzV30hXu6t3OcWGIJ54YUX5IZZs2ZN7lbqJ3kiAMFce+21eX6X7g+3bt0q58Y59u3b1xw8eDDdp6THTwCBwBAMbeditEqcJIBF6H6CPgyBikT4esWoL0T5VfqySZMmZt++fV45NT2PBBAIFMGQKUuMh5o9BAiH50amqF26jTiTp556Sqa55557rlm9enW6T0mP7wACgSIYgqy4YYhWVbOHQKFChSQk3t7Wzm/FiGXevHnivEUQC2cupWrUgoFAoAiGuAUIZtCgQcHonRS0YvTo0TJq2Lx5cwqOlv0QVEWkblPFihXNgAEDQicjkR2NYP4XKIL5/vvvDeHeV155pWp42LxeifGAlMk+TpXh80H4iqqTxLNQ59kPy+WpwidIxwkUwdAxrCJxw2jJCXuXKWJKBK4hsOS2hANRuPhZcCxXrVpVIondPqY9FHQrtxAIHMF8/PHHQjBej+9wq0MT2e+0adMEMzenSStXrhRSKVCggPhZdMSSSE/57zeBIxiekmh64DCMRwvEf13n3BnjC3Fr1Mcyc4MGDWT/jJJw6qqFB4HAEQxdR5YtNwzJa2qxEWCaRAg+/iunlNyQMUXAiehqfGJu5A3FbplukW4EAkkwCDcTSzFmzJh04+ub47OaBCkfOnQoqXMmb2jChAmSSEmIP3KV6mdJClJf/ziQBEOPMBwvUqSI5q7YvDwXLVokBIMweKL20ksvmVq1apkqVaoYMtw1UTBRJIPzu8ASDE9RnsgnTpwITm+52BKW+OvVqyfTmXgPs3fvXtOiRQvBm7whrR4ZL4LB3T6wBINzsUyZMqLpEdzuc7ZlvXr1EpKwu1cibocPHy6/wc+iPi+7yIVnu8ASDF2IKjyjGDV7CFipFpSDiWZff/21YWmbKShypSqKHQ2tcH8X6LtvypQpQjBHjx4Ndy/H0foaNWqIsFNeP8FZ+9Zbb8k0qmTJkmbIkCFGqznkhZR+ZiEQaILhhuApS41hNXsI9OzZM9eoD5U3/CpU0kRqE0kM9bPYwzPsWwWaYOjcq6++OtcNE/ZOj9Z+6gExrezUqZOUANm1a5dBbb9y5cqC5fr163XUEg1A/S4bAoEnGKsesyrdZev3fP+x4mEgGWKJyHRGYwfFwC+++CLf3+kXikBeCASeYGg0N8vNN9+cV/v1swgEiOKtVKmS4AVmvCCXbdu2RWylbxUB+wiEgmBq164tRdDtwxLOLUl2xHlrkQt/27Rp41j6QDhRDXerQ0EwW7ZskZuGVSW13AiQN4RsJjIKjFiYGp1xxhnid6FEiJoikCgCoSAYwOFpTPqA2s8IEOVMDAukQtkXyoJg77//voGMteDYz1jpu8QQCL44aUAAAAdXSURBVA3BdO7c2Vx88cXm8OHDiSEVoF+hxbJu3TpzzTXXiEbL4MGDzYEDBwLUQm2KVxAIDcEgF8AoJuyC4IxK2rZtK/EsxLXwP3EuThmF0SjqpqYIgEBoCIbCXRAMNYfDahRxL1q0qETiMoJJNgoXaQamWJEaMqQZkNOkpgiAQGgI5ocffjBMBcqVK2f27NkTqt6n/GpGRoY566yzZATnlD4LqQKQtjXtRK2ObOoZM2aECl9tbP4IhIZggOD111+XG+LVV1/NH5EAffPuu++axo0bS5sp5k6SolO2YcMGifaNnHYiUUqVAK1r5BTK/t9PqAgG3ZIKFSoYpgpBNsL9KQtSrFgxCTB0esTG1Kp///7m8ccfl/KukyZNEjhXrFihNamCfGEl0LZQEQz43HPPPaZw4cLm888/TwAub/+EekOPPfaYISO6fv36rpVu2bRpkyxtf/LJJ6K7a/lcIJhkJTe9jbCeXbwIhI5gnn/+eZkyBC0beM6cORLLgvATJVvcVPIjnmjs2LFyrU2ePFmmYfxz+vTpeK8/3T7gCISOYIhaJagsKEF3H3zwgalbt66E+LNCdvz4cVcvWSsqunTp0qZmzZriOK5WrZqrx9Sd+xeB0BEMXdWhQwcZxfi324z55ptvjKXd0qRJk6yVHLfbVL58edGDIYVgyZIlUkEAR6+aIpAXAqG8Mgi246bwY2E2piFIKlDXmbIgrOakypBswH8VaQTWKcFEIqLvIxEIJcEAAPWYKTbmF2PE8sorr8i0BFU5AtqI7UmVETsDkbDUH2lUI+DztWvXRn6s7xUBQSC0BGOV2fD6dUAYP/EshPeT5Uy1xHSsgL3zzjumS5cuecJFqd79+/fn+Z1+GG4EQkswKNzx5PWy0h15Qty8OFHRweUmV1ME/IRAaAmGToJgGjVq5Mn+GjVqlCQk4sBdvny5OHU9eaJ6UopAFARCTTANGjQwpUqVigJP6r8iCZG8Ic5r5syZSSckpr4FekRF4GcEQk0w+DIYxfzud7/7GZE0vSOcv3nz5nI+AwcOTNNZ6GEVAWcRCDXBACUEk05BcISeIBTkKnE8+3Hp3NlLUvcWJARCTzDk0aCkn+ocmpMnT4osZfXq1Q2i5PhZ1BSBoCEQeoJhpYZRDDk1qTDiSYiCpSAcEp5Tp041p06dSsWh9RiKQMoRCD3BMJKgvCzLwW4beTytWrWSZed7773XkI2c07Zu3WrGjRtn0G8ha1lNEfAzAqEnGDrvkUceEaU7yqS6YUS7op9SqFAh07FjxzwLmSHEffvtt5vLL7/c9OnTR95TVRF5CTVFwK8IKMEYY95++22ZJi1YsMDxfly4cKHsu0qVKiYzMzPq/vEDRarBbdy4UTK/qQetpgj4EQElGGOkZAfRskxbGEkka4T3v/HGG6ZOnTpCLrNnz05ol9u3bxfxqDfffDOh3+uPFIF0I6AE81MPjBkzxhQsWNDs27cvqT4huxmtmbJly8q0COX9eAyhKKZq7Gf48OHm7rvvVidwPADqtp5CQAnmp+6wpjJMlxIx5CqHDRsmUxryhqjDlIgtXbpUkgopigZJkeiopgj4FQElmJ967tixY6ZWrVqGYmTxFCJDRoGQfsTEyRtatmxZUtKR+GGQ80S4m9WkevXqaZKjX+8uPe/w1EWy09f9+vUTn4ndukHkDV1xxRVSfhUdXOoCOWnovRBlPHHiRCd3q/tSBFKGQGhHMMS/5BTGpmAYQXc7duyI2gHffvutxLOwLeVB4vWzRN15xJcch+oASjARoOhbXyEQSoIh/wdy6N27d67OQsgaUfD8jJpK/JaCZkeOHMlvs7g/Z1pE2sK0adPMokWL5IWUBHEx6RCYirsB+gNFIA8EQkkwRO2ef/75Mr3JiUn37t2FQCI/p/Yy5VeZDvG71atXR37tyHu0bSGX6667zlSuXFkyq8ePH2+OHj3qyP51J4pAOhAIHcEQtEaZj6efftqgkJ/TrLpJRNVS2B2nLXKVjGoeffRRw7RFTRFQBOwhECqCIYiOVaKHHnpIguuY6kQazl2rpAnf8YJYhg4dakiKVFMEFIH4EMh+h8X3W99tvXLlSpHIPHz4sJw7BBLpoCU0HzU5i1z4iwiU3VUl3wGiJ6wIuIxAaAiGekJt2rQRmQTiVubNmydEErliRHYzPpZIgrHqLrvcD7p7RSCQCISGYNBggTiIkCV4rWHDhqZAgQJm+vTp2TrWWqpm26pVq5q9e/dm+17/UQQUAfsIhIJg8L3UqFFDisJHQtO0aVPxx0R+xnscuW5JN+Q8lv6vCAQZgVAQzJQpUySvJ2emNLorjGTUFAFFwB0EQkEwEAnJjDkNHVyU49QUAUXAHQRCQTD5ad6yOuR0/pA73aR7VQT8iUAoCMafXaNnrQj4HwElGP/3obZAEfAsAkownu0aPTFFwP8IKMH4vw+1BYqAZxFQgvFs1+iJKQL+R0AJxv99qC1QBDyLgBKMZ7tGT0wR8D8CSjD+70NtgSLgWQT+D2VOJczzOrlUAAAAAElFTkSuQmCC[/img][br]What is the length of segment [math]BB'[/math]?
Elena thinks length BC is 16.5 units. Lin thinks the length of BC is 17.1 units.
Do you agree with either of them?
Explain or show your reasoning.
Mai thinks knowing the measures of 2 sides is enough to show triangle similarity. Do you agree? Explain or show your reasoning in the applet below.
Line g is dilated with a center of dilation at A. The image is line f.
Approximate the scale factor.