
Figure 1. On the side of the can, it is mentioned that 12 g of yeast has been used per hectolitre, or 100 litres.
Table 3 presents a summary of the most common multiples in use. In the first column, a prefix is written, in the second column, these prefixes are together with the meter of the base unit of length. In the third column, the prefixes are combined with the unit of volume cubic metre and in the fourth colloquial language with the more common unit of volume. The last two columns describe what is done when moving up or down. If you want to convert centimetres to millimetres, i.e. move upwards, then multiply the number by the number 10 mentioned in the top row. This multiplier is [b]used every time[/b] you move up one row. If you want to convert centimeters to decimeters, then divide the number by 10.
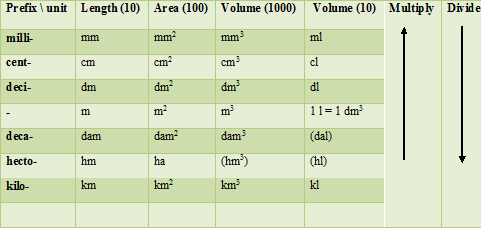
Table 3. The most common multiples used in Finland.
Table 1 of the SI system describes the basic units. For example, the basic unit of length is the metre and the kilogram of mass. These are the units used in the calculation. Colloquially, it is more common to use multiples of these. For example, the length of a car trip is more likely to be described in kilometres and the weight of a spider in grams. Another example is that a cardboard strawberry box is designed with length measurements. In this case, its volume is obtained in cubic meters. However, in practice, volume is described in litres. [br][br][br]The unit prefix, e.g. [b]kilometer[/b], describes the size of the unit in relation to the base unit. Table 4 shows the most common multiples and their identifiers. The power notation in the last column [br]gives a numeric form to the multiple unit. [br][br][br] [math]1\text{ km} = 1\cdot 10^3\text{ m}=1000 \text{ m}\\[br] 1\text{ cm}=1\cdot 10^{-2}\text{ m}=0.01\text{ m}[/math][br][br] [br]If volume is solved with units of length but the context requires solution in litres, transformation can be done with [br][br] [math]\large\textcolor{blue}{1\text{ l}=1\text{ dm}^3.}[/math] [br][br]

Table 4. Multiples, their symbols and multiplier in powers of 10
The last column in Table 4 can be used for multiples exchanges As known, one metre is 100 cm. If we use the previous table, the idea is to[color=#0000ff] subtract power of end case from power of starting case[/color]. In our examples, the starting case is [math]1\text{ m} = 10^\textcolor{blue}{0} \text{ m}[/math] and the end case is [math] 1 \text{ cm} = 10^{\textcolor{purple}{-2}} \text{ m}[/math]. [br][br]The transformation formula could be written as follows using powers:[br] [br][math]\Large 10^{\textcolor{blue}{\text{from where}}-\textcolor{purple}{\text{to where}}} .[/math] [br][br][br]Thus,[br][br] [math] \large 1\text{ m}=1\cdot 10^{\textcolor{blue}{0}-(\textcolor{purple}{-2})}\text{ cm}=1\cdot 10^2\text{ cm}=100\text{ cm}.[/math] [br][br]The same idea is usable also with harder cases. See the examples below.
[u]Lengths:[/u][br][br][math] 2.3\text{ cm}=2.3\cdot 10^{-2-0}\text{ m}=2.3\cdot 0.01 \text{ m}=0.023 \text{ m}\\[br]\vspace{7mm} 0.5\text{ km}=0.5\cdot 10^{3-(-1)}\text{ dm}=0.5\cdot 10^4 \text{ dm}=5000 \text{ dm}[/math][br][br][u]Area:[/u][br][br][math] 1\text{ m}^2=1\cdot (10^{0-(-2)}\text{ cm})^2=1\cdot (10^2)^2\text{ cm}^2=10^4\text{ cm}^2=10000\text{ cm}^2\\[br]\vspace{7mm} 0.01\text{ ha}=0.01\cdot (10^{2-0}\text{ m})^2=0.01\cdot 10^4 \text{ m}^2=1\cdot 10^2 \text{ m}^2=100\text{ m}^2\\[br]\vspace{7mm} 4.7\text{ dm}^2=4.7\cdot (10^{-1-(-2)}\text{ cm})^2=4.7\cdot 10^2 \text{ cm}^2=470\text{ cm}^2[/math][br][br][u]Volume:[/u][br][br][math] 1\text{ m}^3=1\cdot (10^{0-(-1)}\text{ dm})^3=1\cdot (10^1)^3\text{ dm}^3=10^3\text{ dm}^3=1000\text{ dm}^3=1000\text{ }\cal l\\[br]\vspace{7mm} 2\text{ }\cal l=2 \text{ dm}^3=2\cdot (10^{0-1}\text{ m})^3=2\cdot 10^{-3} \text{ m}^3=2\cdot 0.001\text{ m}^3=0.002\text{ m}^3\\[br]\vspace{7mm} 5.2\text{ dl}=5.2\cdot 10^{-1-(-3)}\text{ ml}=5.2\cdot 10^2 \text{ ml}=520\text{ ml}\\[br]\vspace{7mm} 3.1\text{ dl}=0.31 \text{ }\cal l=0.31 \text{ dm}^3=0.31\cdot 1000 \text{ cm}^3=310\text{ cm}^3[br][br][/math]
[color=#0000ff]Example 2[/color]. Wind speed is informed to be 18 m/s. What speed of a car does it correspond?[br][br]Speed of a car is usually given as km/h. Let us transform the given wind speed to this unit:[br][br] [math]18 \text{ m/s} = 18 \frac{10^{-3}\text{ km} }{\frac{1}{60\cdot 60}\text{ h}}=18\cdot \frac{3600}{10^3} \text{ km/h}\approx 64.8 \text{km/h}.[/math][br][br][br][br][color=#0000ff]Example 3[/color]. It is noticed, that there is dropping water from a pipe with a speed of 60 litres in two hours. Calculation need units in SI system, so let us transform it to m[sup]3[/sup]/s. [br][br] [math] \frac{60\text{ l}}{2\text{ h}}= \frac{60\text{ dm}^3}{2\cdot 60\cdot 60\text{ s}}=\frac{(10^{-1})^3\text{ m}^3}{2\cdot 60 \text{ s}}\approx 8.3\cdot 10^{-6}\text{ m}^3\text{/s}.[/math][br] [br][br]



