Castillos y Cuadriláteros
De ruta por la comarca de La Serena podemos visitar varios castillos que se erigieron como fortalezas defensivas antes las diferentes invasiones que sufrieron sus habitantes. Algunos de estos castillos se conservan en buen estado y pueden ser visitados. Nos centraremos en cuatro de ellos por su carácter de atalaya desde las que divisamos gran parte de la comarca: Magacela, Benquerencia, Capilla y Puebla de Alcocer, este último en la comarca de la Siberia. [br]
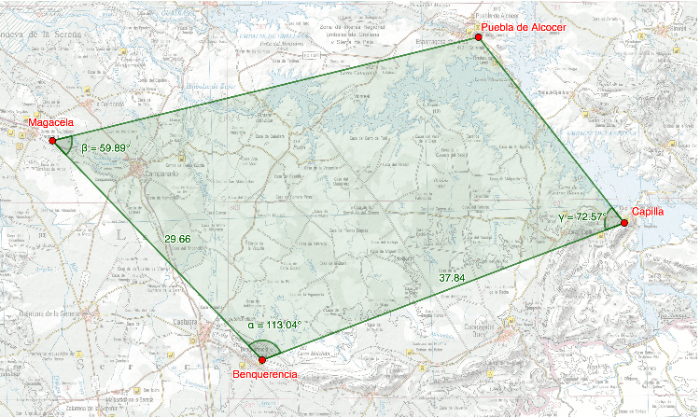
Observa el cuadrilátero que hemos construido con vértice en cada castillo.

TAREA 1
Teniendo en cuenta los datos que se dan , construye un cuadrilátero igual. La escala del plano es 1:100000
TAREA 2
Indica el ángulo que desde Puebla de Alcocer se observa Magacela y Capilla
TAREA 2
Teniendo en cuenta que la escala del plano es 1:100000, indica la distancia real en línea recta desde Puebla de Alcocer a Capilla.
TAREA 4
Vamos a comprobar el Teorema de Van Aubel en el cuadrilátero construido en la tarea 1. [br]El teorema afirma que los segmentos que unen los centros de los cuadrados sobre los lados opuestos del cuadrilátero son iguales y perpendiculares.
DETALLE DE LA CONSTRUCCIÓN
[list][*]Construimos un cuadrado sobre cada lado del cuadrilátero, de manera que el cuadrado quede dibujado en el exterior del cuadrilátero.[/*][*]Marcamos el centro de cada cuadrado.[/*][*]Trazamos los segmentos que unen los centros de los cuadrados sobre lados opuestos.[/*][*]Hallamos la medida de cada segmento y comprobamos que miden lo mismo y son perpendiculares.[/*][/list]
TAREA 5
Un cuadrilátero se dice que es cíclico o inscrito si sus cuatro vértices se encuentran sobre la misma circunferencia.[br][list][*]Comprueba si es cíclico el cuadrilátero de la tarea 1.[/*][*]¿Cuánto han de sumar los ángulos opuestos para que un cuadrilátero sea cíclico?[/*][/list]
TAREA 6
Realiza la siguiente construcción:[br][list][*]Sobre el mismo cuadrilátero de la tarea 1 trazamos los triángulos formados por vértices consecutivos, obteniendo así cuatro triángulos.[/*][*]Hallamos el baricentro de cada triángulo.[/*][*]Trazamos el cuadrilátero cuyos vértices son los baricentros obtenidos. [/*][*]Halla P[sub]1[/sub]=perímetro del cuadrilátero mayor y P[sub]2[/sub]=perímetro del cuadrilátero menor.[/*][*]Halla A[sub]1[/sub]=área del cuadrilátero mayor y A[sub]2[/sub]=área del cuadrilátero menor.[/*][/list]
TAREA 7
Halla la razón entre [math]\frac{P_{^{_1}}}{P_2}[/math] y la razón entre [math]\frac{A_1}{A_2}[/math].[br]¿Qué observas?
TAREA 8
Si habitases en la zona delimitada por el cuadrilátero y tuvieses que huir buscando refugio, a qué castillo te dirigirías. Representa la solución geométricamente.
Referencia:
Todas las imágenes que aparecen en esta actividad han sido tomadas de la web [url=https://www.ign.es/web/ign/portal]Instituto Geográfico Nacional[/url] y tienen licencia CC-BY