Differential Geometry: Curvature

What is Differential Geometry?
"Differential geometry provides the language and theory to understand the geometry of curved surfaces."[br] - [i]Thinking Geometrically, Thomas Q. Sibley[/i][b][br][br]Differential Geometry[/b] is the study of smooth [b]manifolds[/b]. [b]Manifolds[/b] are multi-dimensional spaces that locally (on a small scale) look like Euclidean n-dimensional space. [br][br]Ancient Greeks found that some curves will 'bend' more at some points on the line than others; consider a parabola for example. However, most concepts involving the curvature of a plane only become relevant with Calculus.[br][br]Sir Isaac Newton developed the correct formulation for curvature, but didn't publish his work! This allowed Gottlieb Wilhelm Leibniz (another founder of Calculus) to publish his findings on [b]curvature[/b]. A few years later, Jakob Bernoulli published his work on [b]geodesics[/b] and [b]surfaces of revolution[/b].[br][br]A few decades later, Alexis-Claude Clairaut and Leonhard Euler analyzed how much such curves twisted out of a plane, now called the [b]torsion [/b]of a curve. Once curvature started becoming more popular, Carl Friedrich Gauss developed many advancements in differential geometry. One of his profound theorems generalizes some theorems you may know.[br]
Gauss-Bonnet Theorem (for geodesic triangles)
In Spherical Geometry we have:[br] The area of a spherical triangle is proportional to the difference between its angle sum and π. More precisely, on a sphere with radius r, the area of a spherical triangle with angle measures of α, β, and γ is [br][center](α + β + γ − π)r[sup]2[/sup].[/center]In Hyperbolic Geometry we have[br] In hyperbolic geometry the difference between π and the angle sum of a triangle is proportional to the area of the triangle.[br][center]π − (α + β + γ)[/center]Gauss-Bonnet Theorem (for geodesic triangles):[br] Suppose a triangular region T of [i]any[/i] smooth surface is bounded by geodesics and the measures of the angles made by the geodesics are α, β, and γ . Assume that T can be shrunk continuously to a point on the[br]surface. Then,[br][center]α + β + γ − π = [math]\int\int_T\kappa\left(u,v\right)d\sigma[/math] where κ(u, v) is the curvature at (u, v).[/center]
What is Curvature?
In simple terms, curvature is how fast a line bends. The literal definition of curvature is rate of change in direction over a certain interval:[br][center][math]\kappa=\left|\frac{d\theta}{ds}\right|[/math][br]where [math]d\theta[/math] is change in direction and [math]ds[/math] is change in arc length[/center]If you have taken any Calculus course, "rate of change" should trigger a bell in your head. Maybe you are thinking of something like slope or a derivative. And that's exactly right! Curvature is derived using derivatives. There is a geometric solution to curvature, but it uses perpendicular bisectors which become very hard to analytically calculate with complex curves. Hence, why curvature is a big part of [i]differential[/i] geometry.[br][br][br]The formula for curvature is:[br][center][math]\kappa\left(x\right)=\left|\frac{f''\left(x\right)}{\left(1+f'\left(x\right)^2\right)^{\frac{3}{2}}}\right|[/math][/center]There are several ways to derive this formula, here's a generally straight forward one:[br][list=1][*]Start with our basic definition[br][math]\kappa=\frac{d\theta}{ds}[/math][/*][*]But break it down in terms of [math]dx[/math] instead of [math]ds[/math][br][math]\frac{d\theta}{ds}=\frac{d\theta}{dx}\cdot\frac{dx}{ds}[/math][/*][*]Now to solve for [math]\frac{d\theta}{dx}[/math]:[br][math]\theta=tan^{-1}\left(f'\left(x\right)\right)[/math][br][math]f'\left(x\right)[/math] is the slope at x, and by using arctan we get [math]\theta[/math][br]So to get [math]\frac{d\theta}{dx}[/math] simply take the derivative of this formula: [math]\frac{d\theta}{dx}=\frac{d}{dx}\left(tan^{-1}\left(f'\left(x_{ }\right)\right)\right)[/math][br][math]\frac{d\theta}{dx}=\frac{f''\left(x\right)}{1+f'\left(x\right)^2}[/math][br][br][/*][*]Now solve for [math]\frac{dx}{ds}[/math][br]We have from arc length:[br][math]ds=\sqrt{1+f'\left(x\right)^2}dx[/math][br][math]\frac{dx}{ds}=\frac{1}{\sqrt{1+f'\left(x\right)^2}}[/math][br][/*][*]So multiply the two together we get:[br][math]\frac{d\theta}{dx}\frac{dx}{ds}=\frac{f''\left(x\right)}{1+f'\left(x\right)^2}\frac{1}{\sqrt{1+f'\left(x\right)^2}}=\frac{f''\left(x\right)}{\left(1+f'\left(x\right)^2\right)^{\frac{3}{2}}}[/math][br][/*][/list]
Radius of Curvature
An equivalent definition for curvature is based on a term called the [b]osculating circle[/b]. The osculating circle is circle that has these 3 properties:[br][list=1][*]Tangent to the curve at point P[/*][*]Has the same curvature to the curve at point P[/*][*]Lies on the concave side of the curve[/*][/list]If we use this definition, curvature can be represented as:[br][center][math]\kappa=\frac{1}{R}[/math][br]where R is the radius of the osculating circle.[/center]
In two dimensions, it is conventional to use the absolute value for the curvature value. This is due to the intuition that you can't become 'less curved' than 0 aka a straight line. Furthermore, it with two-dimensional curves, there is only one direction of curvature. Any line will only bend in one direction. In three dimensions, many of these properties will not hold.[br][br]Three dimensional surfaces are a bit more complex than just one line curve. A surface is made up of infinite curves. This means any one point has infinite curvature values. With these infinite curvature values, it becomes difficult to say 'how curved' a surface is if it can bend in many different ways. In fact, curvature has to be redefined to accommodate these three-dimensional properties.
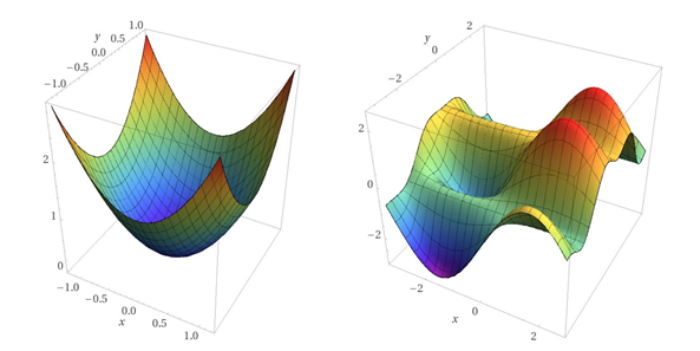
Gaussian Curvature
[left][b]Gaussian curvature[/b], created by Carl Friedrich Gauss, is a unique interpretation of curvature that allows us to interpret curved surfaces in higher dimensions. In 3 dimensions, curvature is specified by 2 principal curvatures, the [b]minimum[/b] and [b]maximum[/b]. By multiplying these two curvatures together, we get the curvature value for the point on the plane.[/left]The parity (or sign) of this curvature is determined by which way the surface curves.[br][list=1][*]The curvature is [b]positive[/b] if all curves bend the same direction (all inwards or all outwards). This is typical of a [b]dome[/b] shaped surface. Another way to think about it, is all the curves seem to converge/bend towards the same point.[/*][*]The curvature is [b]negative[/b] if some curves bend one direction and some curves bend another direction. This is typical of [b]saddle[/b] shaped surfaces. Traveling on the surface of a saddle you may start traveling in the positive x direction, but at some point may begin bending in two different directions based on which curve you follow. [/*][*]The curvature is [b]zero[/b] if the surface is flat. It only need to be considered "flat" at one point for the curvature value to be zero. Take for instance a cylinder, on it's side the cylinder is not flat, however if you consider the top of a cylinder, it is flat.[/*][/list]
Curvature of a Torus
Back to Triangles
So now that we have the basics of curvature, what can we learn about geodesic triangles? Well, let's return to the Gaussian-Bonnet Formula from before. Recall:[br][center]α + β + γ = [math]\int\int_T\kappa\left(u,v\right)d\sigma+\pi[/math] [/center]The double integral represents the area of the geodesic triangle. Then, when we add π, we get the sum of the interior angles. (recall: Sum of the interior angles plus π = area) So,[br][list=1][*]What happens if you plug some constant positive value in for the curvature value? You will get some positive value for the area of the triangle. Then, that means that the sum of the interior angles [i]must[/i] be greater than π![/*][*]Well what happens when you plug in some constant negative value for the curvature value? Similarly, you will get some negative value as the area of the triangle. Well, that means the sum of the interior angles [i]must[/i] be less than π![/*][*]Finally, what happens if we plug 0 in for the curvature value? The double integral goes to 0 and we just get that the sum of the interior angles is π.[/*][/list]This should make intuitive sense given what we have learned about spherical and hyperbolic geometry. A sphere (with constant positive curvature) will have a sum of interior angles greater than π. Similarly, in hyperbolic geometry, the curvature is constant and negative, thus giving us a sum of interior angles less than π. And obviously on a surface with 0 curvature (a flat plane) the sum of the interior angles is exactly π just as we learned in school.[br][br]
Final Words
Curvature is the backbone of Differential Geometry, but what uses could we get out of this crazy arithmetic? For starters, curvature is a fundamental principle in air travel. But, maybe more relevant to mathematics and computer science, curvature is a huge piece in the cutting edge field of machine learning and optimization. Some optimization algorithms like gradient descent, conjugate gradient, and simulated annealing will try to find the minimum (or maximum) of a function by calculating considering the curvature of a function.