Această aplicaţie ilustrează construcţia:[br][list][*] unei suprafeţe obţinute prin desfăşurarea cercurilor meridiane ale torului pe planul de ecuaţie [i]z = - r;[/i][/*][*]familiei de curbe corespunzătoare spiralei de pe tor;[/*][/list]cu ajutorul cursorului [b]v[/b].[br]Cursorul [b]u[/b] permite modificarea măsurii arcului de cerc al centrelor instantanee de rotaţie, al spiralei.[br]Cursorul [b]n [/b]permite modificarea numărului de spire.[br]Caseta "[b][i]tor[/i][/b]" permite vizualizarea/ascunderea torului.

Această aplicaţie ilustrează construcţia unei suprafeţe echivalente cu suprafaţa torului.

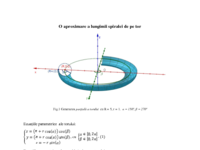
Aplicaţia următoare ilustrează trei aproximări ale lungimii reduse ([math]\frac{L}{R}[/math]) a unei spire a spiralei de pe un tor, cu ajutorul unor arii.[br]Pentru calcularea valorilor numerice ale aproximărilor s-a utilizat comanda [br][i]Integrală(,,).[/i][br]Cu ajutorul cursoarelor din partea stângă a ferestrei pot fi modificate:[br][list][*]măsura arcului de cerc al centrelor instantanee de rotaţie, [b]u[/b];[/*][*]numărul de spire ale spiralei de pe tor, [b]n[/b];[/*][*]raportul dintre raza minoră şi raza majoră a torului, [math]\rho=\frac{r}{R}[/math][/*][/list]

Aplicaţia următoare conţine reprezentările grafice ale aproximărilor lungimii reduse a unei spire în funcţie de [math]\rho=\frac{r}{R}[/math], pentru [math]u=2\pi[/math].[br]Cursorul[b] n [/b]permite modificarea numărului de spire.