Discovering Mathematics for IB DP AA & AI
Dive into IB Diploma Programme Mathematics with our GeoGebra book, tailored for both Analysis & Approaches and Applications & Interpretations courses. This interactive guide offers dynamic activities and exercises, blending conceptual understanding with practical application. Explore calculus, statistics, and real-world problems through engaging tutorials and visualizations. Designed for self-study and classroom use, it's the perfect tool for students aiming to master their IB DP Mathematics exams with confidence.
Table of Contents
- Algebra
- Arithmetic (AA/AI SL 1.2)
- Graph Trans (AASL 2.11, AIHL 2.8)
- Rational functions (AAHL 2.13) quadratic over linear
- Binomial theorem (AAHL 1.10)
- Rational functions (AA HL 2.13) (Linear over quadratic)
- Graph trans. (AAHL 2.16)
- Geometric (AA/AI SL 1.3)
- Investigating general parabola (AASL 2.6)
- Factorising quadratics, sketching and inequalities
- Completing the square and vertex form (AASL 2.6)
- Sum of geometric series (AA SL 1.8, AI HL 1.11)
- Log rules (AA SL 1.7, AI HL 1.9)
- Indices laws (AASL 1.5/1.7)
- Binomial theorem (AASL 1.5)
- Inverse functions
- Composite functions
- Rational functions AASL
- Chain rule (AASL/HL)
- Log graph transformations
- The Cosine Rule
- Discriminant
- Equations of straight lines (AASL2.1)
- Complex numbers AAHL 1.11,1.12
- Calculus
- Tangent and normals at a point (AA/AI SL 5.4)
- Second derivative - AASL 5.7/5.8 AI HL 5.10
- Trapezium rule (AI SL 5.8)
- Phase portraits (AI HL 5.17)
- Maclaurin series
- Partial fractions (AAHL 1.11)
- Eulers method visualised (AI HL 5.16)
- Derivative of x^n
- Product rule (AASL/HL)
- Quotient rule (AASL/HL)
- Integration of functions of f(ax+b) AASL 5.10
- Integral calculus - Area AASL5.11
- Integration by parts AAHL5.20
- Statistics
- Sampling distribution from a normal distribution
- Cognitive activator - Lift overloading
- Cognitive activator - Shooting Arrows A&A
- Normal distribution (AI SL 4.9)
- Linear regression/correlation coefficient (AA/AI SL 4.4, )
- Geometry and trigonometry
- Trigonometric graphs (domains, ranges sin,cos,tan,arctan,arcsin,arccos,cosec,sec,cot)
- Motion with variable velocity in 2D
- Vector applications in kinematics
- Adding sinusoidal waves (AI HL 1.13)
- 3D Vectors (addition, subtraction, multiplication by scalar, unit vectors and magnitude)
- Degrees-Radians, area of sector and length of arcs
- Distance and midpoints (3D) - AI/AA SL 3.1
- Angle between a line and a plane
- Angle between lines (3D)
- Angle between two lines (2D)
- Equation of perpendicular bisector (AI SL 3.5)
- Powers of matrices (AI HL 1.15)
- Further explorations with Voronoi (AI SL 3.6)
- Voronoi (exploring) - AI SL 3.6
- Transformation matrices (AI HL 3.9)
- Eigenvalues and vectors (AI HL 1.15)
- Angles in the four quadrants (Unit circle)
- Discover double angles (AASL 3.6)
- The Sine Rule
- The Cosine Rule
- Trigonometric graphs (Radians and degrees)
- Number
- Venn diagrams and number sets (self-checking)
- Scientific notation (AA/AI SL 1.1)
- Depreciation (AA/AI SL 1.4)
- Applying to the real world
- Applying DP Mathematics to the real-world
- Graph Theory
- Graph theory (AIHL 3.15, 3.16) - Part 1 Definitions and basics
- Graph theory (AIHL 3.15, 3.16) - Part 2 Adjacency
- Graph theory (AIHL 3.15, 3.16) - Part 3 Minimum Spanning Trees
- Graph theory (AIHL 3.15, 3.16) - Part 4 Travelling Salesman Problem
- Graph theory (AIHL 3.15, 3.16) - Part 5 Chinese Postman Problem
Arithmetic (AA/AI SL 1.2)
Keywords
[table][br][tr][/tr][br][tr][br][td]Arithmetic Sequences[/td][br][td]等差数列（とうさすうれつ）[/td][br][td]等差数列（děng chā shù liè）[/td][br][td]등차 수열 (deungcha suyeol)[/td][br][/tr][br][tr][br][td]Arithmetic Series[/td][br][td]等差シリーズ（とうさシリーズ）[/td][br][td]等差级数（děng chā jí shù）[/td][br][td]등차 시리즈 (deungcha sirijeu)[/td][br][/tr][br][tr][br][td]nth term formula[/td][br][td]n番目の項の公式（nばんめのこうのこうしき）[/td][br][td]第n项公式（dì n xiàng gōng shì）[/td][br][td]n번째 항의 공식 (nbeonjjae hang-ui gongsik)[/td][br][/tr][br][tr][br][td]Sum of the first n terms[/td][br][td]初項からn項までの和（しょこうからnこうまでのわ）[/td][br][td]前n项和（qián n xiàng hé）[/td][br][td]첫 n 항의 합 (cheot n hang-ui hap)[/td][br][/tr][br][tr][br][td]Common difference[/td][br][td]公差（こうさ）[/td][br][td]公差（gōng chā）[/td][br][td]공차 (gongcha)[/td][br][/tr][br][/table]
Inqury questions
[table][br][tr][br] [td][b]Factual Inquiry Questions[/b][br] [list][br] [*]What is the formula for the nth term of an arithmetic sequence?[br] [*]How is the sum of the first n terms of an arithmetic series calculated?[br] [/list][br] [/td][br] [td][b]Conceptual Inquiry Questions[/b][br] [list][br] [*]Why does the formula for the sum of an arithmetic series involve multiplying the average of the first and last terms by the number of terms?[br] [*]How can understanding arithmetic sequences and series aid in solving real-world problems, such as planning finances or scheduling tasks?[br] [/list][br] [/td][br] [td][b]Debatable Inquiry Questions[/b][br] [list][br] [*]Is the study of arithmetic sequences and series more applicable to everyday life than that of geometric sequences and series? Why or why not?[br] [*]Can the principles of arithmetic sequences and series be effectively used to understand patterns in nature and society?[br] [/list][br] [/td][br][/tr][br][/table][br]
The Arithmetic Adventure
Exploration Title: "The Arithmetic Adventure"[br][br]Objective:[br]Embark on an arithmetic adventure to discover the hidden treasures of sequences and series. Use the powers of addition and difference to navigate through the world of arithmetic progression.[br][br]Mission Steps:[br][br]1. Term Treasure Hunt:[br] - Calculate the 100th term of the sequence that begins with 5 and has a common difference of 7.[br] - Compare the 100th term with the 1st term and discuss how quickly the terms grow.[br][br]2. Sum Saga:[br] - Find the sum of the first 50 terms of the sequence you investigated in step 1.[br] - How does this sum relate to the individual terms of the sequence?[br][br]3. Common Difference Challenge:[br] - Change the common difference to -3. What happens to the sequence?[br] - How does a negative common difference affect the sum of the series?[br][br]Questions for Investigation:[br][br]1. Patterns of Progression:[br] - Why does an arithmetic series with a positive common difference grow without bound?[br][br]2. Sum vs. Term:[br] - How does the sum of the terms compare to the value of the last term in a long arithmetic sequence?[br][br]3. Practical Applications:[br] - Where do you encounter arithmetic sequences in real life? (Think savings plans, paying off debt, etc.)[br][br]Engagement Activities:[br][br]- "Sequence Prediction": Without calculation, predict whether the 200th term will be an even or odd number for a given first term and common difference.[br]- "Sum Duel": Compete with a partner to see who can calculate the sum of the first 'n' terms of a sequence faster.[br][br]Dive into this arithmetic expedition, uncover the linear patterns of sequences, and unveil the accumulating power of series. Happy calculating![br]
Part 2 - Checking understanding
Watch the two videos below before attempting the questions
Alternatively these videos are very short, and work through exam-style questions directly.[br][br] Arithmetic sequences 1 [url=https://youtu.be/jJCRJ1XOq9s]https://youtu.be/jJCRJ1XOq9s[/url] Arithmetic sequences 2 [url=https://youtu.be/Q9jTuF6KX6k]https://youtu.be/Q9jTuF6KX6k[/url] Arithmetic sequences 3 [url=https://youtu.be/hZN9VGVSygQ]https://youtu.be/hZN9VGVSygQ[/url] [br]
What is the common difference of the arithmetic sequence 4, 7, 10, 13, ...?
Given the first term of an arithmetic sequence is 5 and the common difference is 3, what is the 10th term?
The 3rd term of an arithmetic sequence is 9 and the 8th term is 24. What is the first term?
If the sum of the first n terms of an arithmetic sequence is given by [math]S_n=3n^2+5n[/math] what is the common difference?
Practical applications centred around life in China
Part 3 - Testing your understanding with exam-style questions
Testing your understanding with exam-style questions
[MAA 1.2-1.3] ARITHMETIC SEQUENCES
[MAA 1.2-1.3] ARITHMETIC SEQUENCES_solutions
Lesson Plan- The Arithmetic Adventure
Arithmetic- Intuition pump (thought experiments and analogies)
Tangent and normals at a point (AA/AI SL 5.4)
Keywords
[table][br][tr][br][td]English[/td][br][td]Japanese[/td][br][td]Korean[/td][br][td]Chinese Simplified[/td][br][/tr][br][tr][br][td]Tangent Line Equation[/td][br][td]接線の方程式[/td][br][td]접선의 방정식[/td][br][td]切线方程[/td][br][/tr][br][tr][br][td]Normal Line[/td][br][td]法線[/td][br][td]법선[/td][br][td]法线[/td][br][/tr][br][tr][br][td]Differential Calculus[/td][br][td]微分計算法[/td][br][td]미분 계산법[/td][br][td]微分学[/td][br][/tr][br][tr][br][td]Derivative[/td][br][td]導関数[/td][br][td]도함수[/td][br][td]导数[/td][br][/tr][br][tr][br][td]Slope[/td][br][td]傾き[/td][br][td]기울기[/td][br][td]斜率[/td][br][/tr][br][tr][br][td]Negative Reciprocal[/td][br][td]負の逆数[/td][br][td]음의 역수[/td][br][td]负倒数[/td][br][/tr][br][tr][br][td]Coordinates[/td][br][td]座標[/td][br][td]좌표[/td][br][td]坐标[/td][br][/tr][br][/table][br]
[table][br][tr][br][td][b]Factual Inquiry Questions[/b][/td][br][td][b]Conceptual Inquiry Questions[/b][/td][br][td][b]Debatable Inquiry Questions[/b][/td][br][/tr][br][tr][br][td]What is the formula for finding the equation of a tangent line to a curve at a given point?[/td][br][td]Why is the derivative of a function at a point used to find the slope of the tangent line at that point?[/td][br][td]In the context of mathematical modeling, is the analysis of tangent lines more critical than that of normal lines, or do they hold equal importance?[/td][br][/tr][br][tr][br][td]How is the normal line to a curve at a particular point defined in differential calculus?[/td][br][td]How does the concept of a normal line relate to the tangent line at the same point on a curve, and what does it signify about the curve's geometry?[/td][br][td]Can the study of tangents and normals provide insights into non-mathematical fields such as economics and social sciences? How?[/td][br][/tr][br][tr][br][td][/td][br][td][/td][br][td]How might advancements in computational methods impact the application and significance of tangents and normals in solving real-world problems?[/td][br][/tr][br][/table][br]
Tangents and normals
Scenario: The Mysterious Hills of Functionland[br][br]Background: In the fantastical realm of Functionland, the landscape is shaped by mathematical functions. A legendary hill shaped like the function[math]f(x)=x^2[/math] has a path that runs straight to the top, but the locals believe it's enchanted because no one can see the path directly—only its tangent and normal lines at any given point.[br][br]Objective:[br]As an aspiring mathematical mage, you're tasked with uncovering the secrets of the hill's path using the magic of calculus to find the equations of these invisible lines.[br]
2. Unveiling the Tangent Line:[br] - Use the derivative of the hill's function to find the slope of the tangent line at your chosen point.[br] - Calculate the y-intercept of the tangent line using the point-slope formula.[br] - Reveal the equation of the tangent line and describe its magical properties.
3. Revealing the Normal Line:[br] - Use the negative reciprocal of the tangent's slope to find the slope of the normal line.[br] - Calculate the y-intercept of the normal line using the point-slope formula.[br] - State the equation of the normal line and explain its mystical significance.
Questions for Investigation:[br][br]1. Discovery Question:[br] - If you were to pick another point on the hill, how would the equations of the tangent and normal lines change?[br]
Investigation Steps:[br][br]1. Finding the Path's Coordinate:[br] - Choose a point on the hill's path and determine its coordinates.
2. Understanding Slopes:[br] - Why does the normal line have a negative reciprocal slope compared to the tangent line?[br]
Part 2 - Checking understanding
Check out these two videos to see it with the calculator[br]
Reflection[br] - How might the equations of the tangent and normal lines help a traveler navigate the hidden paths of Functionland?[br] - In what ways do the concepts of tangents and normals connect to the real world?
[MAA 5.4] TANGENT AND NORMAL LINES
[MAA 5.4] TANGENT AND NORMAL LINES_solutions
Tangent and normals at a point- Intuition pump (thought experiments and analogies)
Sampling distribution from a normal distribution
Sampling distribution from a normal distribution
Background:A renowned chocolatier claims their signature chocolate bars are always precisely 110 grams, with a variance of 32 grams squared due to the handcrafted nature of their products. You, a quality control analyst, are skeptical and decide to investigate if the chocolatier's claim holds.Objective:[br]Your mission is to analyze samples of chocolate bars to determine if they indeed average 110 grams with the variance stated.Investigation Steps:[list=1][*]Understanding the Distribution:[list][*]You'll assume the weight of chocolate bars follows a normal distribution.[/*][*]The theoretical distribution has a mean (μ) of 110 and a variance (σ^2) of 32.[/*][/list][/*][*]Sampling:[list][*]You decide to take random samples of size 6 from the production line.[/*][*]You will repeat this process 100 times to create a dataset of sample means.[/*][/list][/*][*]Statistical Analysis:[list][*]Analyze the sample means to determine if they align with the chocolatier's claim.[/*][*]Compare the experimental mean and variance to the theoretical values.[/*][/list][/*][*]Central Limit Theorem:[list][*]Explain how the Central Limit Theorem applies to the distribution of your sample means.[/*][*]How does the distribution of sample means compare to the original distribution of individual chocolate bar weights?[/*][/list][/*][*]Decision Making:[list][*]Based on the observed sample mean and variance, decide if the chocolatier's claim is likely to be true.[/*][*]What would be the implications if the actual average weight is significantly different from 110 grams?[/*][/list][/*][/list]Questions for Investigation:[list=1][*]Discovery Question:[list][*]If you found the average weight of your samples to be significantly more or less than 110 grams, what could be some potential reasons?[/*][/list][/*][*]Understanding Variance:[list][*]How would you explain the concept of variance to someone with no statistical background, using the chocolate bar weights as an example?[/*][/list][/*][*]Real-world Applications:[list][*]Why is it important for the chocolatier to maintain the weight close to 110 grams, and what could be the consequences of failing to do so?[/*][/list][/*][*]Reflection:[list][*]How does understanding sampling distribution help businesses ensure quality control?[/*][*]What are some limitations of using sample data to estimate population parameters?[/*][/list][/*][/list]
Lesson plan - Exploring Sampling Distributions with Chocolate Bars
Sampling distribution from a normal distribution- Intuition pump (thought experiments and analogies)
Trigonometric graphs (domains, ranges sin,cos,tan,arctan,arcsin,arccos,cosec,sec,cot)
Keywords
[table][br][br][tr][br][td]Trigonometric graphs[/td][br][td]三角関数のグラフ[/td][br][td]삼각함수 그래프[/td][br][td]三角函数图[/td][br][/tr][br][tr][br][td]Domains and ranges[/td][br][td]定義域及び値域[/td][br][td]정의역 및 치역[/td][br][td]定义域和值域[/td][br][/tr][br][tr][br][td]Sine[/td][br][td]サイン[/td][br][td]사인[/td][br][td]正弦[/td][br][/tr][br][tr][br][td]Cosine[/td][br][td]コサイン[/td][br][td]코사인[/td][br][td]余弦[/td][br][/tr][br][tr][br][td]Tangent[/td][br][td]タンジェント[/td][br][td]탄젠트[/td][br][td]正切[/td][br][/tr][br][tr][br][td]Arcsin[/td][br][td]アークサイン[/td][br][td]아크사인[/td][br][td]反正弦[/td][br][/tr][br][tr][br][td]Arccos[/td][br][td]アークコサイン[/td][br][td]아크코사인[/td][br][td]反余弦[/td][br][/tr][br][tr][br][td]Arctan[/td][br][td]アークタンジェント[/td][br][td]아크탄젠트[/td][br][td]反正切[/td][br][/tr][br][tr][br][td]Cosec[/td][br][td]コセカント[/td][br][td]코시컨트[/td][br][td]余割[/td][br][/tr][br][tr][br][td]Sec[/td][br][td]セカント[/td][br][td]시컨트[/td][br][td]正割[/td][br][/tr][br][tr][br][td]Cot[/td][br][td]コタンジェント[/td][br][td]코탄젠트[/td][br][td]余切[/td][br][/tr][br][tr][br][td]Periodic nature[/td][br][td]周期性[/td][br][td]주기성[/td][br][td]周期性[/td][br][/tr][br][tr][br][td]Inverse trigonometric functions[/td][br][td]逆三角関数[/td][br][td]역삼각함수[/td][br][td]反三角函数[/td][br][/tr][br][/table][br]
[table][br][tr][br][td][b]Factual Questions[/b][/td][br][td][b]Conceptual Questions[/b][/td][br][td][b]Debatable Questions[/b][/td][br][/tr][br][tr][br][td]What are the domains and ranges of the sine, cosine, and tangent functions?[/td][br][td]Why do inverse trigonometric functions have restricted domains?[/td][br][td]How can the limitations of trigonometric functions in complex scenarios impact their practical application in fields like engineering?[/td][br][/tr][br][tr][br][td]How does the periodic nature of sine and cosine relate to their graphs?[/td][br][td]In what ways do the domains and ranges of trigonometric functions reflect their applications in real-world scenarios?[/td][br][td]Is the traditional teaching method of trigonometric functions adequate for students to appreciate their practical applications?[/td][br][/tr][br][tr][br][td]How are trigonometric functions used in real-world scenarios, such as in engineering or navigation?[/td][br][td]How do the properties of trigonometric graphs assist in understanding the behavior of periodic phenomena?[/td][br][td]Should the focus of education on trigonometry be shifted more towards its computational aspects rather than its theoretical underpinnings?[/td][br][/tr][br][/table][br]
The Festival of Trig functions
Scenario: The Festival of Functions[br][br]Background:[br]The land of Mathematica is having its annual Festival of Functions, a celebration where the citizens revel in the beauty and utility of mathematical functions. This year's theme is the mesmerizing world of trigonometry, featuring the sine, cosine, tangent, and their inverse functions.[br][br]Objective:[br]As a Mathemagician-in-training, your challenge is to master the graphs of these trigonometric functions, understand their domains and ranges, and use this knowledge to amaze the festival-goers.[br][br]Investigation Steps:[br][br]1. Unraveling the Sine and Cosine:[br] - Begin by exploring the periodic nature of the sine and cosine functions.[br] - Identify the domain and range of these functions and explain their significance.[br][br]2. Tackling the Tangent and Cotangent:[br] - Investigate how the tangent function differs from sine and cosine in terms of its graph, domain, and range.[br] - Do the same for the cotangent function and discuss its unique properties.[br][br]3. Discovering the Arcs and Inverses:[br] - Delve into the world of inverse trigonometric functions, starting with arcsin and arccos.[br] - Understand their restricted domains and ranges to ensure they are functions.[br][br]4. Applying Knowledge at the Festival:[br] - Use your understanding to create interactive displays that help visitors visualize these functions and their importance.[br][br]Questions for Investigation:[br][br]1. Discovery Question:[br] - Why do inverse trigonometric functions have restricted domains, and how do these restrictions affect their graphs?[br][br]2. Practical Applications:[br] - How are trigonometric functions used in real-world scenarios, such as engineering or navigation?[br][br]3. Festival Challenges:[br] - Can you design a game for the festival that involves estimating angles using trigonometric functions?[br][br]4. Reflection:[br] - Reflect on how the symmetry of the sine and cosine functions is represented in their graphs.[br]
Lesson plan - Exploring Trigonometric Functions at the Festival of Functions
Venn diagrams and number sets (self-checking)
Keywords
Venn Diagram,Number Sets,Intersection,Union,Set Theory,Complement,Real Numbers,Rational Numbers,Irrational Numbers,Natural Numbers,Integers,Universal Set,Prime Numbers,Even Numbers,Mathematical Reasoning,Set Relationships[br]
Inquiry questions
[table][br][tr][br][td][b]Factual Questions[/b][br]1. What is a Venn diagram?[br][br]2. Draw a Venn diagram for the sets A = {1, 2, 3} and B = {3, 4, 5}.[br][br]3. How do you represent the intersection of two sets using a Venn diagram?[br][br]4. Illustrate the union of sets A and B where A = {x | x is a prime number} and B = {x | x is an even number}.[br][br]5. Show using a Venn diagram the complement of set A in the universal set U.[br][/td][br][br][td][b]Conceptual Questions[/b][br]1. Explain the significance of overlapping regions in a Venn diagram.[br][br]2. Discuss how Venn diagrams facilitate understanding of set theory concepts like union, intersection, and complement.[br][br]3. How do Venn diagrams help in solving problems involving multiple sets?[br][br]4. Explain the difference between the intersection and union of sets as depicted in Venn diagrams.[br][br]5. Compare the use of Venn diagrams in representing simple vs. complex set relationships.[br][/td][br][br][td][b]Debatable Questions[/b][br]1. Is the use of Venn diagrams more intuitive than algebraic methods for understanding set theory? Why or why not?[br][br]2. Debate the effectiveness of Venn diagrams in teaching logical reasoning and critical thinking.[br][br]3. Can Venn diagrams be considered a universal tool for representing all types of set relationships?[br][br]4. Discuss the statement: "The simplicity of Venn diagrams masks their power in mathematical reasoning."[br][br]5. Evaluate the impact of Venn diagrams on students' ability to visualize and solve problems involving sets.[br][/td][br][/tr][br][/table][br][br]
Scenario: The Quest for Numerical Knowledge[br][br]Background:[br]In the mystical kingdom of Numeralia, understanding the various types of numbers and their relationships is considered a rite of passage for all young scholars. The Grand Library of Numeralia has an interactive exhibit that features a magical Venn diagram displaying real, rational, irrational, natural numbers, and integers.[br][br]Objective:[br]As a young scholar, you are eager to prove your knowledge. Your quest is to categorize different numbers correctly using the enchanted Venn diagram at the Grand Library.[br][br]Investigation Steps:[br][br]1. Sorting the Numbers:[br] - You are presented with various numbers like √3, -16, π/2, and 2/3.[br] - Determine which category each number belongs to: natural numbers, integers, rational numbers, irrational numbers, or real numbers.[br][br]2. Mastering the Categories:[br] - Use your knowledge to place each number in the correct section of the Venn diagram.[br] - Explain why each number belongs to its specific category.[br][br]3. Challenging Misconceptions:[br] - Identify common misconceptions about these number sets and clarify them.[br][br]4. The Library's Test:[br] - The exhibit will reveal if you have placed the numbers correctly and offer explanations for any mistakes.[br][br]Questions for Investigation:[br][br]1. Discovery Question:[br] - Why is zero so special, and what sets does it belong to?[br][br]2. Understanding Number Sets:[br] - How do rational and irrational numbers differ, and why are they both within the realm of real numbers?[br][br]3. Practical Application:[br] - Can you find examples of irrational and rational numbers in everyday life?[br][br]4. Reflection:[br] - Why is it important to understand the different categories of numbers?[br]
Venn diagrams and probability Questions (exam style)
[MAA 4.5-4.7] PROBABILITY I (VENN DIAGRAMS - TABLES)_solutions
Lesson plan - Exploring Number Sets with Venn Diagrams in DP Mathematics
Venn diagrams and number sets- Intuition pump (thought experiments and analogies)
Applying DP Mathematics to the real-world
1Arithmetic_sequences
1Unit_circle.pdf
1Trigonometry_more.pdf
1Statistics_calculating_with_GDC.pdf
1Sine_cosine_questions.pdf
1Quadratics.pdf
1Probability_Venn_diagrams.pdf
1Probability-Tree-diagrams.pdf
1Normal_distribution_questions.pdf
1Logarithms.pdf
1Linear_regression.pdf
1Integration_by_substitution.pdf
1Geometric_sequence_questions.pdf
1Exponential_growth_and_decay.pdf
1Differential_calculus.pdf
1Binomial_theorem.pdf
1Binomial_distribution.pdf
Graph theory (AIHL 3.15, 3.16) - Part 1 Definitions and basics
Inquiry questions
[table][br][tr][br][td][b]Factual Questions:[/b][br]]How are vertices and edges defined within the context of graph theory?[br][br]What distinguishes a simple graph from a complete graph and a weighted graph?[br][br]Explain the concepts of adjacent vertices, adjacent edges, and the degree of a vertex with examples.[br][/td][br][br][td][b]Conceptual Questions:[/b][br]How do directed graphs differ from undirected graphs, and what implications do these differences have for graph traversal?[br][br]Discuss the significance of the concepts of in-degree and out-degree in understanding directed graphs.[br][br]In what ways do trees, as a type of subgraph, uniquely contribute to the study of graph theory?[br][/td][br][br][td][b]Debatable Questions:[/b][br]Considering the constraints and definitions of Eulerian and Hamiltonian paths, which concept offers greater insight or utility in solving real-world problems?[br][br]Can the distinction between simple, complete, and weighted graphs be seen as merely theoretical, or do these distinctions have practical implications in fields like computer science and network analysis?[br][br]Is the classification of graphs into directed and undirected overly simplistic given the complexity of modern networked systems?[br][/td][br][/tr][br][/table][br]
Definitions
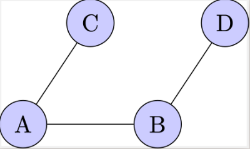
[b]Graphs[/b]: A graph is a collection of points, called vertices, which may be interconnected by lines called edges.[br][b]Vertices[/b]: Also known as nodes, these are the fundamental units from which graphs are formed.[br][b]Edges[/b]: These are the connections between vertices in a graph.[br][b]Adjacent vertices[/b]: Two vertices are adjacent if they are connected by a single edge.[br][b]Adjacent edges[/b]: Two edges are adjacent if they share a common vertex.[br][b]Degree of a vertex[/b]: This refers to the number of edges incident to (or emanating from) a vertex.[br][br]For example,
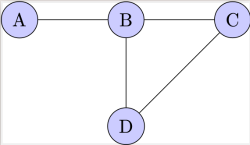
[b]Adjacent vertices[br][/b]Vertices A and B are adjacent because they are connected by a single edge.[br]Similarly, B and D are adjacent, as are C and D.[br] [br][b]Adjacent edges[br][/b]Edges A-B and B-C are adjacent because they share a common vertex, B.[br]Similarly, B-D and C-D are adjacent because they share vertex D.[br] [br] [b]Degree of a vertex[br][/b] Degree of B is 3 because there are three edges incident to B (A-B, B-C, B-D).[br] Degree of C, and D are 2, as two edges are incident to each of these vertices.
[b]Simple Graphs[/b]: A simple graph is an unweighted, undirected graph containing no loops (edges connected at both ends to the same vertex) and no more than one edge between any two different vertices..[br]
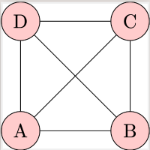
[b]Complete Graphs[/b]: A complete graph is a simple graph in which every pair of distinct vertices is connected by a unique edge. This means in a complete graph with n vertices, every vertex has an edge to every other vertex
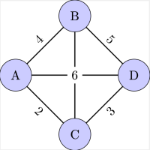
[b]Weighted Graphs[/b]: A weighted graph is a graph in which each edge is assigned a weight or cost. This is useful in problems where the edges have some value, like the distance between two locations on a map.
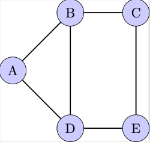
[b]Connected[/b]: In the context of graph theory, a graph is connected if there is a path from any vertex to any other vertex in the graph. This means it's possible to get from any one vertex to any other by a sequence of edges. For example,
[b]Directed Graphs:[/b] These are graphs where the edges have a direction, indicated by arrows. Each edge connects an ordered pair of vertices and points from one vertex (the tail) to another (the head). Directed graphs are also known as digraphs.[br][b][br]Strongly Connected[/b]: This term applies to directed graphs. A directed graph is strongly connected if there is a directed path from any vertex to every other vertex. That means you can start at any vertex and follow the direction of the arrows to reach any other vertex.
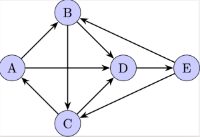
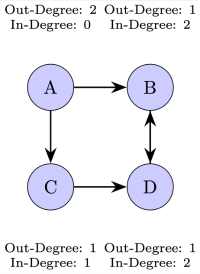
In-Degree and Out-Degree of a Directed Graph: The in-degree of a vertex is the number of edges pointing to it, while the out-degree is the number of edges that the vertex points to. In other words, in-degree counts the incoming arrows to a vertex, and out-degree counts the outgoing arrows from a vertex.[br]
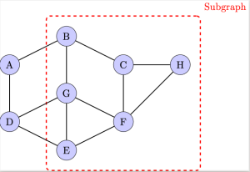
Subgraphs: A subgraph is a graph formed from a subset of the vertices and edges of another graph. It retains the connections that were present in the larger graph.[br]
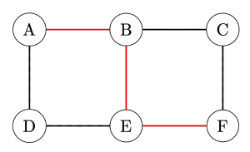
Trees: A tree is a special type of graph that is connected and has no cycles. This means there is exactly one path between any two vertices in a tree. Trees are a type of subgraph where any two vertices are connected by exactly one path.[br]
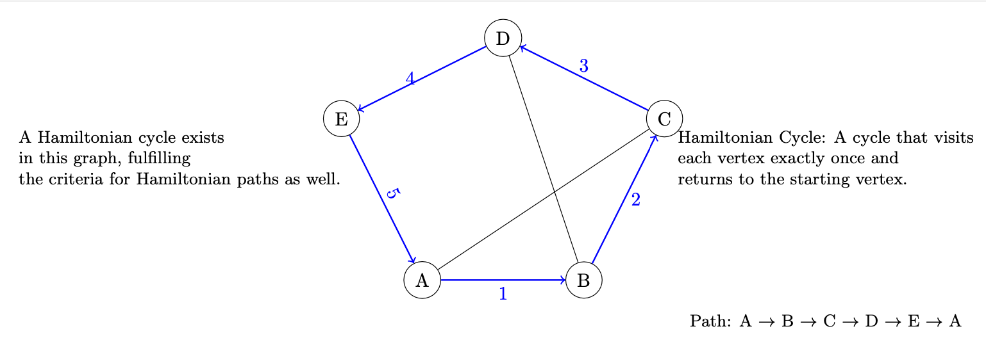
AHL 3.16[br][br]Tree and Cycle Algorithms with Undirected Graphs: This refers to algorithms that operate on undirected graphs to identify trees (graphs with no cycles) and cycles (closed paths where the first and last vertices are the same).[br][br]Walks, Trails, Paths, Circuits, Cycles: These are different ways to traverse graphs.[br][br]• Walk: A sequence of edges and vertices wherein vertices (and possibly edges) can be repeated.[br]• Trail: A walk where no edges are repeated.[br]• Path: A trail where no vertices are repeated.[br]• Circuit: A trail that starts and ends at the same vertex.[br]• Cycle: A circuit that only repeats the starting/ending vertex.[br]
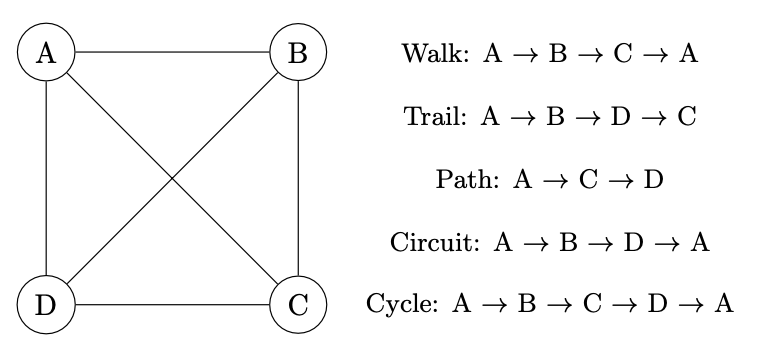
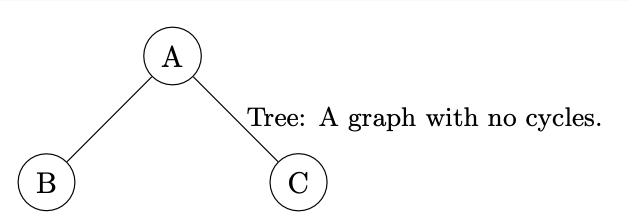
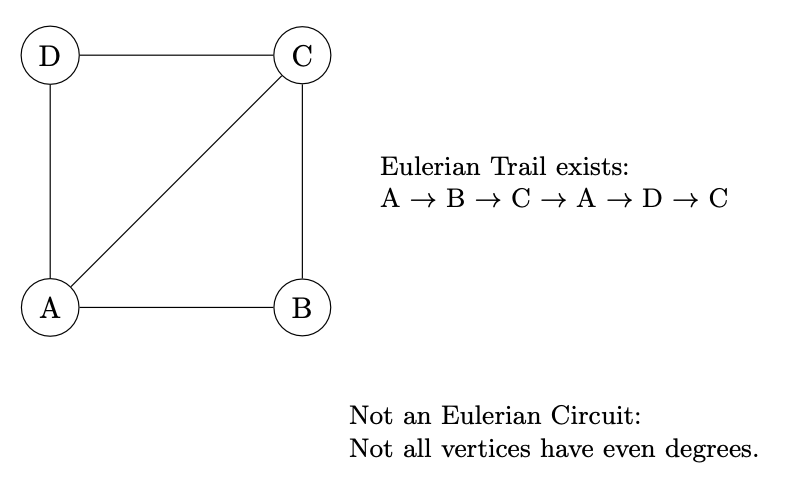
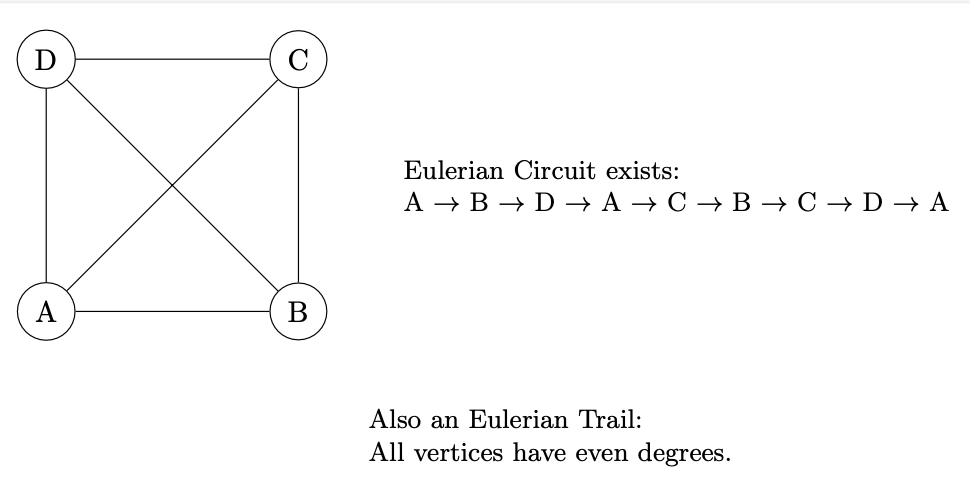
Eulerian Trails and Circuits: An Eulerian trail is a trail in a graph that visits every edge exactly once. If such a trail exists that starts and ends at the same vertex, it’s called an Eulerian circuit.
Hamiltonian Paths and Cycles: A Hamiltonian path is a path that visits each vertex in the graph exactly once; if the path is a cycle, then it’s called a Hamiltonian cycle.
Lesson plan - Introduction to Graph Theory
