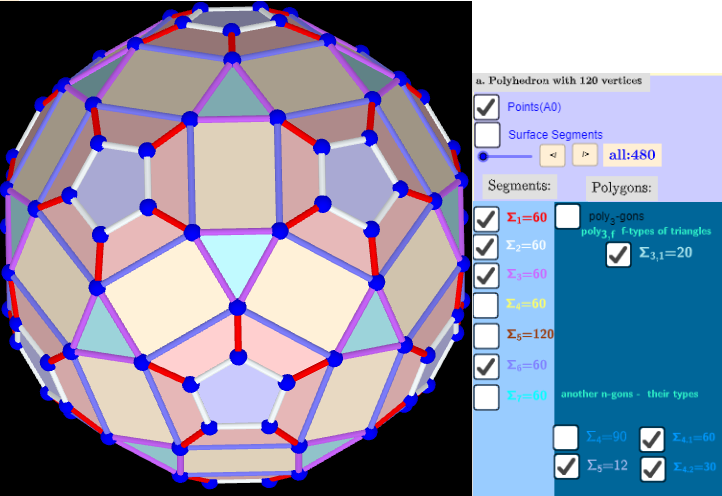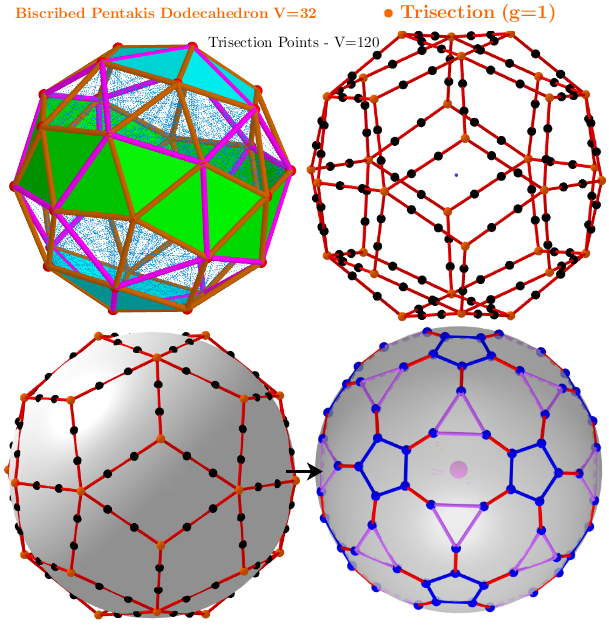
Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
[size=85] A polyhedron is constructed whose V=120 vertices are the points of the trisection of the segments the same length 1st-order (g=1) of the [url=https://www.geogebra.org/m/hczvuvhg]Biscribed Pentakis Dodecahedron[/url]. [br] Geometric Constructions are in [url=https://www.geogebra.org/m/p4a5zccm]Applet[/url]: Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron, and the resulting polyhedra in [url=https://www.geogebra.org/m/uej4qnte]Applet[/url]: Serie of polyhedra obtained by trisection (truncation) segments of the Biscribed Pentakis Dodecahedron.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAakAAACbCAYAAADY6WRJAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAC12SURBVHhe7Z19jFVFmvBNIIRgDAnGEA2ZRGIME0KIIRCGMawhGGOMIQTiGsKSjsbBHmRlXBZ3Sa+EEMgS04R1YKcFWUZhVodh0Zn27ZHt14FgEOTtbkAaBMEWxRlH8WMEZ9RxpN7zq/a5Xbeoc8+555770fj88cuteuo59XlOPfVx7qmrzp49axRFURSlEVEjpSiKojQsaqQURVGUhkWNlKIoitKwqJFSFCU1hw8fNgsXLjRXX311MFxR8qakkeJGvOqqqwoMGTLEDB8+3IwbN87eqEePHi3SrdaN68eN+7rrrivSqQTiSpt39Nw6GTp0qBkzZoxpbm42p06dCl5TK0aOHGlGjRoVDAO/HsvBLzdwL0yYMMEsXbo0l7KX0w6VQjr1uocGK7fccou55pprCu0f0lGUvClppEI3Y1dXl3n44YetfOrUqQU5D2i1HlI/btIeNmxYkU4lEFfah85P+/Tp04X6WLBgQZFuVu68804zc+bMYFgpyEOpclTSRqG4Dx06ZJYtW2YHLxirSg1VOe1QKaRTr3tosBO6FxSlWpRtpKCvr8/KmUX4YbWAtOvVwYTSlvoYMWJEkTwrWTs8rslyXRpKxf3oo4/aMIx1KDwttezoSade99Bgh3J+V8qq1J+yjdTLL79s7rnnHivnV+Tf+973LLjb2trM9ddfb43YDTfcYNauXVvQY7Td1NRkR/SEf//73zcvvPBCIZzlBK59/PHHzY033mhnFW7cQNpcO2vWLLvkNHbsWLNnz55COLS0tFg5ehgPZjnHjx+3YQcPHjTjx4+3YTNmzLC/aR869PzO7cyZM1ZOXvCXShsoO+VpbW21y0TEt2rVKhtGfRGXwCyls7PT7N2719x9991Wn3hJa/r06bY9JF65Bjd1ytIfaUndpG2jEG7cPtQnYTfffHNBRnnnzp1r8wm43TqQ60q1Q1I9xt1LaeuKel+3bp259tpri9oAktJOcw+F7uWkeil1bwik46flQnyUn2vJO8/JpEmTbB65V0PXlENS+oqSJ6mMVIj77ruvSJeHC3DzcKHDw7JlyxbbEYgeezeErV+/3vr5ffrppwvhEv/kyZPN7t27rcyN29XZv3+/efbZZ62bh1LCWYJCxr4Zs5zVq1dbPx0a4XQM+Ddu3GiXrHCDXF8K9Hj4xc9Dv3jxYiufPXt2YtoSBx3G8uXL7b4e/lD5xA+bNm2yewI7d+608dIZo3PTTTdddl1HR0dhf8odAKRtoxASdygMCKPTFT/3BzLa55e//KV133///UXXlGqHNPUYdy+lrSsGAKE2SJN2mntIZO69nFQv+EvdG6IDrsxlyZIlNvzWW2+1Bhv3tm3bLjNQGEOJqxQysBFE7soUpVqUNZPigW1vbze33XablS9atKgQ5naA/BLOg+waIBg9erQNixvRSZrsfYnMjdvVwU2ecLvhMht54403inTouPHL5i9y/LhBri+F6Ap0dIySqQvSS0rbjSMufd8Pvb29l9UZOqTv+gHjhBFyZw7g1iO/6IbaKITEHQoDwuhcxS9G0A1nxiJ+KNUOaeox7l4qp66ypp3mHhKZey8n1YtcUyreJBgscc2cOXPsninuSpdiXbLkSVGykmlPqqenx8pZShCZ2wEyuiRMrmfEK3p0FKE4BbnGlblxh3Rwux2kpOFDp+aGu9e7/lIk6SalDSJL6wde/WWEzMsq1AWzubjrgHy4syhI20YhRC8URidMGMZaZKE6dtsoTkf8aerRv14op65C/ixpi47442Sh69x68a/x/WlYuXKlvYaZFAMV3Bs2bAjqZiFLnhQlK5mMFKNU5O7yjtsBslfAKJS1dPTc5TFGjchkpOgTStON29eRUS4jWwnnlXBkjCJF5kJchGcZrSbpJqUNfhy+P9T5ytIMI+J9+/YVyu3q4eZa9jMwQMwI4v4mUKqNQvhpuTz22GM2jGVPkclMA7fk1W1DKNUOaeox7l5KW1dx/jRpp7mHQrKkevGv8f1pIF72B5m10a7Mlv06AgYVEn8pdLlPqSdlGyk2jOXFiXvvvbcg50GTh421/5deeqmwps7DInqyJk9HyoPzxBNP2E5OwkNpunG7OuSF/QfcPIgSLp0mm90YVNJhSWvevHk2nGUQwlmnZ69A4pPrS5Gkm5Q2+HH4flkSOnDggF1eZY9JlqCoV6k3/zrcYmzYrMd/++23F8LTtlEIPy1gL4bykib/nWOZTcIoL/rsvci+oVsHUKod0tRj3L2Utq7i/GnSTnMPhWRJ9eJf4/vjZC7kCQNUyshWQlL6ipInJY2UuxwkMHviLapHHnnEPsCiy+gTeKB5uBnlsozBw7J169aCHqN3womHcP5f44bTibpr/yBxi589F2BvjDhY1nDX/WHNmjWFt6/oRNlIX7FihQ3DuE2cONGGsX4vb8G518fhdvRxlEobuN6d+flxost1yCgjnc6uXbvs6Jg4+eVFBzpj9zrKgUz8sjfBm3z407ZRiLh7gXKytOa+oQYYP94qoxxAXtxZHSS1Q1I9xt1LaeoKd6k2SEo7zT2E37+Xk+olKV8g9e/KXBg8uO1FOgxK0uw9lkIGBS7US0hXUfKipJFSFGXwwUAEAyJ/rpZ9qaTZsqI0ImqkFOUKg/9mYZR4xR3/jh07rN+f1SnKYECNlKJcYbAXxx+MWSZkqY+lv2nTphWMlqIMJtRIKYqiKA2LGilFURSlYVEjpSiKojQsaqQURVGUhkWNlKIoitKwqJFSFEVRGhY1UoqiKErDUnUjxX81GvGf7uTJ/dxM6PMzlVKNOPOAPDVSm/Bn0ylTphQ+b+R/40/JTqV12yj3SrnPUrn6SeQdXxzlpoNunu3j94uNQG5GilNHZ86ceZmcf7rzh0JfXm/IE3kTf7k3RxqI302jUWi0NpFvCHLEBt+x27x5c1DvSiLuecmbtHXb6M9vuc9n3s9zrZ7lctPJu338frERyM1IxRUu70rMi1o0BvE3WoNDo7VJo94j1aQW9x+krdu4/HwX2yYE9VCr9ionnbzbp1b3ZTnkYqTkaASBM406OzttmFQiX6JmVIebM4zk2paWFjN27Fg72uPzLXzV2v+itg/hHM3BEgbglmv4gjTfLuOoCr7uzQgROV+tlq9a88kYft3G4Mwc99wcRmH4OQaCKbCfb47l5sh6woiLfEyfPr3oNFypD/H7JKUhOu6IMOR34yAf1ClfvOb4DPKGXI5YB/KEnK9xo0/979mzpxAOSe0SV88+pdoK7rrrrkI9QdyXuvmSO+mRH+63tWvXFsJK5ZVf2om6JYwyT5o0yerKV/yz1GFS/fhxum0b97yUKmOIvOq2kZ5fCN1b1CXI9Ult6upDqfbI41kG0uBgTL5sT/ykxyeqXJ2ksvvpUOfkRfzz588v+gZjpe2T1C/GPedJ5ShV3+WS20zKr1xXzk2/fPlyu9yAnwIQtmzZMutfuHChPT5i9erV1t/U1HRZPC5yZADn8fA9Mtz333+/DcMNkydPtuf8yDVUInJOpOUoA9GTcPIk+QLCaLBQvoFzrDimYOfOnTbvnIKLDkciuHG4afgkpSE6bhwhP3FwBhLnOYmf8vIVbCkrR0n4cezfv79wphEPqYSnaReJw69nn1JtJUhcrsyHGx0dHoQtW7bYhxJ5Ul45RgQ/x7nQGeHm6BP3mBlk5dRh2vop1bb4QfwQV8Y48qpbiNNDVsvnF/CDe2+RpqSbpk1dfUAnrj3yeJZBdHiu5AwzOn5XJ23ZxY9RwS9no5Fn91klrJL2SeoXxe8/52nKUer+L4eaGCmgknw9GcFxLhB+dPAnfa1ZHmbx42YUIW7wz5diRIA8lA+gAt1KlPA4fToz96EQHW4Y1+9e4yPhcWmEZHF+Pw73wDuRhfxS527Z07SLxOHXs0+ptnJlrk4I8ocOD5U7I0jKK6Na/BxSSJ3g5sReuR6QQdo6LKd+/Dj9cPFDXBnjyKtuIU5P5KFyVOP5FT+495b7fKZpU1cfJM5QOfJ4lsHVkXwxy3B10pZd/Bx4ih8DIF+z91dFIGv7JPWL4vef87TliIu3HMo2UpI5wC3yuEz4ctfPTSB+F6bMoh9CrhM/bqy2uN0wIXSN64+7qeP8bEQzops6daq9juls0jU+afSTdJL8aXRwS/1BmnYRmfjjKNVWriwpLkZ6LFeIbnNzs5Un5XXlypXWz6hbzlXasGFDUdxyTZzfl2WpnyQ/xJUxjrzqFuL0fLnrT1MPIZLyLfGIH9znM02blvM85/EsQ+gavz2ylJ1DZqlT8sj1zEzi9F1/mvYJ5aeUXyi3HL6/HHKbSfmZFkplVg5nc0esaRDrj1tGB3JDuvG7EI48zrKXc1MD6634GcHt27evkI9S1/ik0XdladLw/Uk6Eid1KuFp2sWNoxSl2kpIExfLbowIWddGl44EeVJeSZPTeRlQcQ2zFGSujp++7/dlWerH94eel7gyxpFX3UKjPL/gpiG4z2eaNnX1wY/T9efxLIOrQ53gdvMAWcouRpm9Jf5O4Ib5+q4/TfuQNjpSf+71Ib9Qbjl8fznkZqRkhnXgwAHT3t5up6nIS2WWPQDcrLsy3aawLHMk/ZeDcK5jPRRwyzVu/C4sDSBn7Zq1VV+PCi6nkmUqLWvFsgZd6hqfNPoyqqMDY48iy8gnTodNU9bjcfOgS3iadpE4xB9HqbYS0sTF/gB1LevbMotPyivtzYZvJQbFl2WpH98fel7iyhhHXnULjfL8gpuG4D6fadq0nOc5j2cZRIc6lP0f97mCLGXnfmCWgpw9HjfM13f9adonqV/0/UK55fD95ZCbkVqxYoXtULkxbrvtNlto5PixuqLn3zxr1qwx8nYJ17OBSVwSHoJG440e9IE1apkCE3doTZwOeeLEiTYd9NkEd/PBqAPEn5TvXbt22dEc8fGLAeFmd3X8a3wIK5UGMKpGxto27lAaSXH4MsoOtBP5Z9nEX3NOahfiS9p7gFJtJRCXWwYfHi4eNNa8yQ8d1NatWwvhpfLKZrC7hEY4xoCHVa730/frKyRLUz+l4vSfl2eeeaZkGUPkUbeCn596Pb9A/P695T6fadq0nOc5j2cZJD/yXDHr8Z+rNGUPpYMecftv4aJbSfsk9Yu4Q895mnKUylc55GakFKURoaPi4WYmil/2MJJmKUrj0qhtSh4gFFYpjzzySNHbht8l1EgpVzT8x4OOg9dk8csbUmlmgUpj0qhtSh4gFJaVX//61/YvCRgolu9COlc6aqSUKxr2GfivCksNLEuwTDRt2rRCB6cMPhq1TVmqzXs2x1IcS/38LykU/l1AjZSiKIrSsKiRUhRFURoWNVKKoihKw6JGSlEURWlY1EgpiqIoDYsaKUVRFKVhUSOlKIqiNCy5GSn+s1Crf3zXMq1KGUx5zQvKDKGwWvJdrHtFudIo20hxMuPMmTMvk/NPa/5Y58vTEhdviErTqgbVqpfBSDX+eV8KrXtFuXIp20jx0Ic6oEo7hLh4QzRi51OtehmMUOa0bZkHWveKcuVSlpGST9oLHBvR2dlpw6RD4AvCfB4Et5xpzxHPHHnM0gtf2+UzH5zbz4chk+INUSotSEoP+M6X+2n5+fPnF7791dLSYs9u4Vo+ucLXqd3z+32y1guUm1ZbW5v9dhn6pLt27VorT1Nmlr84O6e1tdXqoUP6fD163Lhx9jrk7smf5eYPpB7EXyoOP09+/aBHuZBzLV9enjRpko2L4wcqqXtFURqfsmdS0hmE5HQQoTPtObOIT8Tv3LnTHrvwwgsv2HD3q75x8YYolRakSY8lIjppwvHzWfk77rjDLFu2zOouXLjQhsm5ME1NTYVrQ6ADIXlcXrOkRUeODp33li1bbAeMPG0d07nzoUqOzBY/Z97wRWmOQEDG5/rRz6MukuLATR7i2pLTSJFxnAiGGDfHSGCgRAcZiN+Vl7pPFEVpfHI1UkBH5OvRIbqdioTTgbh+0U9CdENpQZr0OGcFGR+llA6dDlRG5pyQih5p4E/6wjI6ECcP5TVLWnSy6GBY3PNzyqljPy/u4XEiw51HXSTFIbqh+gE5R4fD2eS0U05QlfDQNb48Lm5FURqf3I1UyH/48GE7Ip46dartZFl2KaWfRNK1adLjsC/8ixcvLozWOVGTTl10XUaPHl24NoToJcldf5a0Nm7caJe9RLe5udnKs9Sx7/dledRFUhziD10LcnQ2Myk5N2jDhg2F8NA1cfI4PUVRGpeyjZR0Or68VIfAngNuRsD79u0rjKZd/bh4Q/jX+v406QH7JBMmTDCTJ0+2J6EikwPVSh1NHSJLvWRJi2U5ZiXsrXAtxgh5mjIn+X1Z1rooJw5XN+SnHJyWKvtVzCBlZiRkqXtFUQYHZRsp2RNh1tHe3m46OjqsvFSHIEs+nANDB/PEE09cph8Xbwj/Wt+fJj3gjBZkdHKyR8J+DTI291k+43qW1dyXLEJkqZcsabHHRLlkj4V0kacpc5Lfl2Wti3LicHVDfvafGECUMpRZ6r6UTFGUxqFsI8X5+IxoWVLiLH86EeT4486037Vrlx0Ns0HOL5v9dKoSDnHxhiiVFqRJT/QwUIBb5OxXjR8/3l5Pnnghgfy51/pkqRcoJy06eDp73lRDn85769atNixNmZPyEpJlqYty4kCvVJ54mcNd3uR6DLW7H5e17kGNlKI0NmUbKUWpJbJcyDInftmXkhmkoihXNmqklIaG/4RhlORo8B07dlh/0huGiqJcGaiRUhoa9thmzJhhl+lY0mPpb9q0aQWjpSjKlY0aKUVRFKVhUSOlKIqiNCxqpBRFUZSGRY2UoiiK0rCokVIURVEaFjVSiqIoSsOiRkpRFEVpWHIxUpdGjDDmqqtK8o33OZq8+eP27earCRPMpaFDzddjxlwWfqGpyebz0vDh5sKCBeasd6xFpfA/nivlKwiNVhb+wDtlyhR7/hefVkr6dqDPldQ2ivJdIxcj9cny5QVj9PmsWUGdavKHjg6Dcbo4d641Pr/fs6co/JOWFpu3j9asMR+vWmXdny5dWqSTFg5LnDlz5mVyvoLAn019+WCk0coi3yrkOBI+rLt58+ag3nehbRqJuPpWlDzJbbnv89mzC4bq44QPkObN53Pm2HTfO3AgGP5FNAon/NyhQ+bcwYPW/eXEiUHdJOjs6PR8uRqp6pE2P9+Ftmkk4upbUfIkNyP1zqlTtuOP7lpjhgwx7ztfFa82fxs92jCT+qy52f6y7OcaLFmOPNvXfw4Rbpb9JDwtchyGwNfTOzs7bZh0hHx9nJE/bs58cq9viWZ0nGHFrIDP+/BFc46Bd3VcWKbinKjW1la7XBWKEx0o5XfjYMmMfPAV8XHjxtm8IF+/fn3hGsqCfFY0K0afPO/xZqdJZeHr43x37/HHH7dfa2fU7V4vcA1nRJEO4Hbjueuuu4rq3P36uUslbVOqLG1tbbYchJHG2rVrU10XImtc/N59990234TRLpMmTbK6chpzlnZOyr8fp1tvcfVdqoyKkoVcX5xgpvK3qBOI7lprON49fDioB+8ePWo+XbLE6rvyr6OHguuTQE+uwSgi+yh6mD7Yts26/3zHHZeFF/yRG2Mm/nKQhzIk50Fdvnx54awn11gsW7bMyhYuXGiP3OCoevxyjlUIwnnY4+IUHSjlJw7OdeKIefFjDPiyOEdhIBs1atRlcezfv988++yz1k0nKeFpyiJxcKDk7t27C3IfOdOLdPgeH+7777+/SEficmUh4vSQxbVNUlnonPHTeW/ZssUaujTXhcgal5wczenEe/futW6OIxEDBcjKaee0bVjq/sMP4oe4MipKVnI1UiDLfsxe3tu3L6jz5S23mG+ikTZ6ENIpBwyOjYeHNnrgcLsvatTKSAEPfEhPRp6cqosfPfylvuYtccTFGZLF+f043EMERRbySz7dzilNWSSOrq6ugiyEdGrix81sx9WRuFxZiDg9kYfqMakslBs/nb07i8vSnlnjmh09U/jnzJlj2w03JzDL9YAM/DLGtXM5bejH6YeLH+LKqChZydVIfRRN7aM71HI+xQhKdENh5YBBwhCJnzhdI8TSnpuODY+MqPjjkA4UcCMLPZghue9nJC8yl9HRjFN0fEQnzp9GJ8mfRgc3I2rxpymLyMQfh8QlftxuWiJLE1ecni93/Ull2bhxo10KE3lzc3Oq60JkjWvlypXWz0xKztPasGFDUdxyTZzfl2VpwyQ/xJVRUbKSm5F6f8cOIzMa+5ZdQMcHXXBlX994Y0FeCne57y/Tp1uZ3XOKwP2Ns3wle2XvRKNKwM2+lYSXg9+pCv4D6/vl8L5Sx6D7JMXpy2Q07Ook+ZN0JE73hNs0ZXHjKAXx+mm5szZIG1eWtkkqC0tlzDbYi0GPfRnkWdoza1zUC6ctM1DiGmYpMrsRuB7i/L4sSxv6/lB9x5VRUbKSi5F6b//+wl4URuad6CYN6fmgD6Gwcvh49Wobz4dtbYU9qQvz5xfCed0c2fn16+0MD3fWV9BldnXgwAHT3t5uOjo6rNx/gH0/ewX42ZxmL4FOhuWQUv/5SYoT6ASQ0Tmw/u93HP41vr+UzsGDB82mTZusm45RwtOUReIQfxxcgx57UrL/5ddJ2riytE1SWTiqnjOtZE9GZtRZ2jNrXOw/8fJJJQbFl2VpQ98fqu+4MoauV5Q05GKkmJVEd18/USd5Keo4XZC5MxtBrvHlWfjTokX9f9aN0uO/WryYUQiPHsCL0cMn+cGd9c+8K1assIaB0f5tt91mOxDk+N3ZBn5/RrBmzRozfvx4u5xFHLfccouNz9VxSRMnI1ZkvM2Fm70GVydNHL6MzXWgfOSVZSZ/bympLMRXan9GoDPjbTXiAPZfkLk6xOWWIY6sbRNXFjpuOnH5nxaGYuvWrYnXSbhLJXHx0oO7hEY4xgCjItcnlTEkS9OGpeL06/uZZ54pWUY1UkoWcn9xohwwUBAKUxSlH1maY7aMX/al3FmKolypqJFSlAaH/x1hlOTIfD4ThT/NTFVRBjtqpBSlwWGPZ8aMGXZZjeU1lv6mTZtWMFqKciVTFyN14b77CgZK4L9TIV1FURTlu0tdZ1KKoiiKUgo1UoqiKErDokZKURRFaVjUSCmKoigNixopRVEUpWFRI6UoiqI0LGqkFEVRlIZFjZSiKIrSsKiRUhRFURoWNVKKoihKw6JGSlEURWlY1EgpiqIoDYsaKUVRFKVhUSOlKIqiNCxqpBRFUZSGZdAaKQ58W7JkSc3QA+YURVFqz6A1UhgOjtCuFT/5yU+C+VAURVGqx6A3Uj/4wQ+sAakWU6dOVSOlKIpSJwa9kaq28ahVOoqiKMrlqJFKQI2UoihK/VAjlYAaKUVRlPqhRioBNVKKoij1Q41UAmqkFEVR6ocaqQTUSCmKotQPNVIJqJFSFEWpH2qkElAjpSiKUj8yG6njx4+bu+++2wwbNsyMGDHCzJo1y0yaNMkMHTrUnDlzJnhNnmQxHqdOnTKPPPJIMCwONVKKomQhS3+TF6G0a5mfPNPKbKSk87711lvN3r17rXvbtm01MVBQrvHg23sYU64JhceRl5Hav3+/GTt2rLn66qvN+vXrgzrVoqury0ycONEOIObOnRvUqQXcKwxqQmHVhHLThrfffnswvNps3brVXHPNNWbp0qXB8Gpx880323ILixYtCupVk+bmZlv/ixcvDoZXE9Ik7cceeywYXk3i+hvyQp5aWlqK5HkSSjtr/5eFUFqV9H+ZjdTs2bNtJubMmWNOnz5t3Q8//HBQtxpkNR7lNlJeRqq1tdVs3rzZvPzyy2bUqFFBnWrR2dlp2trarLGqddrC9u3brZGoh5Eqt83zZvz48WbXrl32OQmFV5s777zTft6L0W0ovJrccMMNpre311x//fXB8GrCvXb48GGbh1B4LfDvvdGjR5v29nZz3XXXFcmrQei+r+Wz4KZVSf+X2UitXLnSZoLRMQnj3rBhQ1C3Ggw2IyX09PSYG2+8MRhWTbhBhgwZUpdRJYwbN87OuOtlpEi3HjMJIO0pU6aYefPmBcOryY4dO8zIkSPtfRcKrzYs+VD/tZ5FAvXOwIyZSyi8Fvj9Dc8gv7XIU6ivC8mqRSitLP1fZiPV19dnlxMYEXAzsIyELKRbDQajkWIp9K677rIdRyi82jCqrMUIzmft2rXmgQcesO56GKl7773XjuaHDx8eDK82dEyHDh2qS/rsFS9fvjwYVgu4344ePWquvfbaYHg1ueeee+zgQI1UaVm18NPK2v9lNlLsP2ER67WEMRiNFEukO3fuDIZVE9aIDxw4YI0Ua8IhnWrCjUkdCrXcG+ro6LD3Kh1lPcoOPCeMIOthpDAO7AeEwmoBZabu61F2ZlEsrTGLD4XXAr+/oT1YeaqF0fbTjpNVCz+trP1fZiPFyFA2x4AR8k033WSefvrpoH7elGs8GElLXoE9gpCeT15G6vHHH7ejKOqp1g8sI5cxY8bY9lq1alVQp1bUeiaFcWBPiDpfvXp1UKfakC4j53q8PECbh+S1gueHsvMbCq8mCxcutAOTTZs2BcOrSVx/wwsT1Ec1X5wIpZ21/8tCKK1K+r/MRopOjwzIZqzsS9VqOSnPGU4papWOoiiKcjmZjRRv69B5s5SEn9E6fjZpfd1qoEZKURTlyiezkXrppZfMjBkz7HSaKRzLCtOmTSsYrWqjRkpRFOXKJ7ORqjdqpBRFUa581EgloEZKURSlfqiRSkCNlKIoSv1QI5WAGilFUZT6oUYqATVSiqIo9UONVAJqpBRFUeqHGqkE1EgpiqLUj0FvpDiCAHe1IH41UoqiKPVh0BupWqFGSlEUpfYMWiPFly0wHLWiXsdrKIqifJcZtEZKURRFufJRI6UoiqI0LGqkFEVRlIZFjZSiKIrSsKiRUhRFURoWNVKKoihXIG8c7jP/tfC4eejq7mD4YKEiI8VBh6H/FLlwKGLo2rz44/bt5qsJE8yloUPN12PGBHUuNDWZS1FeLw0fbi4sWGDOnjkT1Ks269efNxMnfmmGDbtkhg+/ZKZN+8K8/PLvi3Sami5E9dofvmDBBXPmTHEcWTn14nlzZMWXpqv5kun+8SVzdM0X5q3u4rTh+KYLpvuhfp3eJy+Yt/uKwyuh+83t5tkjE8ymrqHmmZ7L2+ql403mqe4REcPNb3sXmL6382un7d1/NBOe/coM3XTJjHnm66BO00tR3T8V1X3Egt9GdZ9j2d/s3m6OPDvBdG0aanqeubzsx19qMt1PjYgYbnp/uyCq9/zKvueP282KryaYBy8NNf/8dfgZ2XShyTx0aYT58aXh5skLUd2fzSf98weeMV8+9/fm0uap5tJTPzBf/KrJ/P74/iKdCy/9WxT2Qxt+4bct5mzfW0XhWVn/4jNm4oq/N8Oap5rhP/6BmbamybzcXZw2NG36NzPioR9anQVPtkTtnk/6UK92X3nLEbP4mm7zo6u6LCEd2LP9TbNiwhHz4NAu889jeoI6WWmK+l1sxPCo310Q9btnMva7FRmp5cuXF4zRrFmzgjrV5A8dHQbjdHHuXGt4fr9nz2U6n7S0mCiD5qM1a8zHq1ZZ96dLl16mV20wNjfd9FezdOmn1r1v33tkxYwd+9eCTkvLJ1a2Zs1HZtWqj60bfTeeLGBoDi//qznxi0+t+60j75muHxlz+F8G0oY3dnxi5Sef/8ic/J+PrZtrXJ2sHDvTYY1T+7G51viceKu4rfa+0WKe7LrKvHJyTcQq6/7diXzaqePYH6xxmtt+0RqePScuN84te6O6fzKq+1eiun8lqvvIvfR3+ZT9zLEO20kda59rO6G3ThSX/Y29LabryavMyVfWRKyy7hO/y6fsr/2hwxqnDRejeo8MT8/vL39GdnzSYn5krjLPf7TG/M/Hq6z7F5/mkH7U2f91+yzz6e9arfu9E68Z8+SkSHZ3QeeTvT+1so9e2WQ+fqXNuq2+G08GMDQ3LZ9llv6i1br3HXnNXPWjSWbsvwykDS07fmrla57fZFb9T5t1c42rk5V6trtQyki91nHGGqcNc4+ZvjNvm549+RnnlqjfxS6sifrdVVG/i3tpxn634uW+2bNn2wzAihUrgjrV4vM5c6zRee/AgWA4fDFlitU5d+iQOXfwoHV/OXFiULfa9Pa+W3BjqKKs2BmTyKZM+cLKDh06Zw4ePGfdzLwkvBLefnMgbQwVBojZkqtzZNUXVt7Xe870HTtn3cy+XJ2svNg7xxqek33httpxZIoNP9V3KNI5aN3PHcmnnea8+Lk1OgdOvhcMhyk7orqPdA6diur+ZFT3kXvic/mUvffFObYD6jsZLvuRHVP6w08dinQOWveR5/Ip+08/n2ONzrH34p+RVV9MsTq95w6ZY+cOWveKL/NJ/90zbwz4I2OBEWLGJLIvdvyDlZ07ddicO9lt3cy8CtdUQO+bA2ljqDBAzJZcnSmr/sHKD/UeNgePdVs3sy9XJyv1bHehlJH66ZxeG3bsQF8wvBKmRP0uNuFQ1O8ejPpd3BMz9rsVG6lTp07ZxMnEkCFDzK5du4J61eBvo0cbZlKfNTfbX5b9fIPFMh+9/dm+/obAzbKfq1MPli37lKyYJUsGRuss8yHr+3aZCbdrxPLijf/+tH+WtK14psAyH/Kzb/f7Q4YsKz/vGW1nUp0nmu0vy36uwWKZD8P09tn+dsLNsp+EV8Lon//NzqSaOz+zvyz7+QaLZT4MU9+3ZcfNsp+rk5Wen4+2I+oTnc32l+Uft+NiuYcO6uzb/WXHzfKPhFfCP/1ttJ1Jbf2s2f6y7OcbLJb5MExS97hZ9nN18uDTPev6Z0r/d21BxjIfMim7b8TyYtl/r7MGaMm2gbSBZT7kfd+mHzJkWalnuwuljNQ/je6xM6mtzSfsL8t+eRks2Qrq+7bfxc2yn6+XhlxenMBaXnvttTYjoyPDcfjw4aBe3kRW0Rqdj1pbzQfbtln3n++4I6hT8EduDJqrU0u2bPnADB3ab4xuv/3PRWHfZrXgx42uq1MJb3Z+YLoe7DdErz9enDZ0P2j6jdS3ftzouzpZ2dQ9xBqeV0+1mu7T26z7+dcH2krCxY8bYyb+ShiyKarXyOi0vvqR2db9gXXf8bxX99/qiB83Bs3VyUr3piG2Azr1aqs53b3Nul9/fqDsEi5+3HRq4q+EB80Qa3TaP2o1ez7YZt2tfy5+RkRH/LgxaK5OJXzw/3aaS5umWAP05+cfLAozmyb3GynxY6QiXVenErZ07jRDH4xG9ZHxuf3x4rRhyIOTbZj4caPv6mSlnu0ulDJSDw7p37Nqbz1l9mw7bd2td7we1C0XJizYA/HjHpqx383FSIEs+2FB9+3bF9TJG4wNPbl9ESKy2Li/8V7UaDQjJWzeHHWWkRGaP/9CQVZtIyWc+t/IWEUGqLdtIG2oqpGKDA6Gh/0oRuy4n+oeaKtqGimMDUaH/ShmSrivfuqbIp1qGik6HjoguykejZpxdz81UPaqGqnI2GB02I+i3nE/9E3xM1JtIyV8cOhX1ghd6FhekFXbSAmb//dX1gDNbxtIG6pppOrZ7kJJIxXNnghjP4otANx5vQnYcEZq7dq1NhOwbt26oE41wCDRs4ufXt03QCztIS/SiQypq1MPWNKLsmLf9BMZS3vIxI+bJUDx50bUUVsD1FwcN0t7vpFiCdDVyQoGCUMkft8IsbTnGymWAMVfCRgkjJD4QwaIpT3fSLEE6OpkhY6JDkn8fmfEEo/fWbEUJP5KwCBhhMQfMkAs7flGiiVAVycXoo7aGqHNUwsylvYuM1JP/bDgzwuW8zBAvOnnylna840US4CuTlbq2e5CKSOFQWI2JX70MFyuTlZY2vONFBMYVyctFRspvg6OhSQTc3nLLqBTLf4yfXq/AWLdU2ZSo0YV6fCSBPJ3Tp+24GbvytWpFbLXJO4oK0VGiJckkJ0+/Y4F94QJXxXCK+LbvRZxhwyQfUUdI/XWOxbcR1bkk/7Oo9Ot4WE0LzOprT0DbcVLEv3hpy242bdy48jK9J1/sUaHWZTMpEZtLZ5J8ZIE8tNvR3UfgZu9K1cnK0d3Tu/vjNh7+HZE3bN1oOxslveHn7bgZv/CjSMr//6X6dboSL3jXvJN8TPCSxLI33rntAU3e1euTmYos+P2jRAvSSB7J5phA+6vnr1n4JoKkH0mcYcMEC9JID/91hkL7gkr8km/nu0ulDJS/z79qA1jFiUzqSWj8nkNXd5TOB31uYB7QsZ+tyIjtX///sJe1I033mjeeMN5k8fhhRdeMCNHjrSZnB4ZFqysbKhVwserV1uj82FbW2FP6sL8+UU6vG6O/Pz69eZ8NMvDXY9X0Hftet9MnvxlVBfvW39b24dkxdx778WCDq+bI+P/VOvWnbfuPF5BP7P/fXN01ZfmzKv9ab+5+0NrgHr/cyBt4HVz5Pyn6mT7eevO6xX0V06utobntTfbCntSHb0DbcXr5sgOnFpvXj25zrrzegV99bevlLe99mFhT2p+R/FSJ6+bI19/IKr7V6O6j9x5vYJ+8pXVtgN687W2wt5Eb8dA2XntGNmpA+vNyVfXWXderyI///Fqa3R2f9hW2JNqu1D8jPC6OfIXz6837efXWXcer6C/f2S3+XLHfPP+0U7r//C156wRuvh/Hi3o8Lo5Mv5Pdf7Vp607j1fQd+3fbSavmm9eeLU/7bbdz1kDdO9/DqQNvG6OnP9UrWt/2rrzegW9nu0ulDJSz68+acN2t71Z2JNqm98b1C0XXjfHLqyP+l1W13DX5RV0jA6JA2uQw4YNKwLZqGhmM2fOHKszefJks3HjxlwMlPCnRYv6/6gbpff5rFnm3aNHi3WitC7Om2fDAXc9/szb03POPPDAZ+aGG762e08jR35j/6x7/Hg0a/lWh9nVvHkX7RIg4M7jz7xvnzhnjm/5zPQs/druO3X/4zf9f9R9cyBtSzTL6P3ZRbsMCLgZYRXpVEDn8UV2CW9z1zDzm2OzohnLQFsxyu/onWfDAHeef+Zd1Pknu3w3bPMlM+s3n5ujpwdeyQdmWPM6orqPwgF3nn/mPd65yC7ldG0eZo79ZpZ5+7Rzn0aj7N6OeTYMcOf1p074+Z8W2eW75kvDzH98PsucfLf4GaHuf3Zxng0H3Hn8mffc6dfNZ7tXmq+fvsPuPX3zX39n/6z7jvtaelT2ix3/2v9n3wjcefyZt+fE6+aBLSvNDUvvsPtOI//x7+wfdY87r6UDM6x5P/tXuwwIuHld3dWphHq1+1P3HS8YKIE/+Pp6P1903Dw0ots0D+sy/zHrmDl59O3LdLJAHz8v6mvFFuCuy59507J48eKCkeJE3ZCOoiiKovjUxEh1dXWZMWPG2I2zjo6OoI6iKIqi+NTESLEnJS9XyHecQnqKoiiK4lITI3XNNddYA9XT02N/WaMM6SmKoiiKS02MFB+ive6666xx4m3ARx8tfsNGURRFUULUxEgpiqIoShbUSCmKoigNixopRVEUpWFRI6UoiqI0LGqkFEVRlIZFjZSiKIrSsKiRUhRFURoWNVKKoihKw6JGSlEURWlQzpr/D28b3POpO9cwAAAAAElFTkSuQmCC[/img][/size]

1. Generating Elements of mesh modeling the surfaces of convex polyhedron and its dual image
2. Coloring edges and faces of polyhedra
[size=85]If we assume that all quadrilaterals lie in the same plane, then our polyhedron approximately looks like[br] [b]Rhombicosidodecahedron :[/b][br][url=https://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/]https://robertlovespi.net/2014/06/02/zonish-versions-of-the-rhombicosidodecahedron/[/url][br]This polyhedron based on adding zones along the five-fold symmetry axes of a rhombicosidodecahedron.[b] [br]All its edges[/b] are the same length, and its [br][b]62 faces[/b] include[br] 20 triangles,[br] 12 regular pentagons and[br] 30 elongated octagons.[/size]
Properties of polyhedra
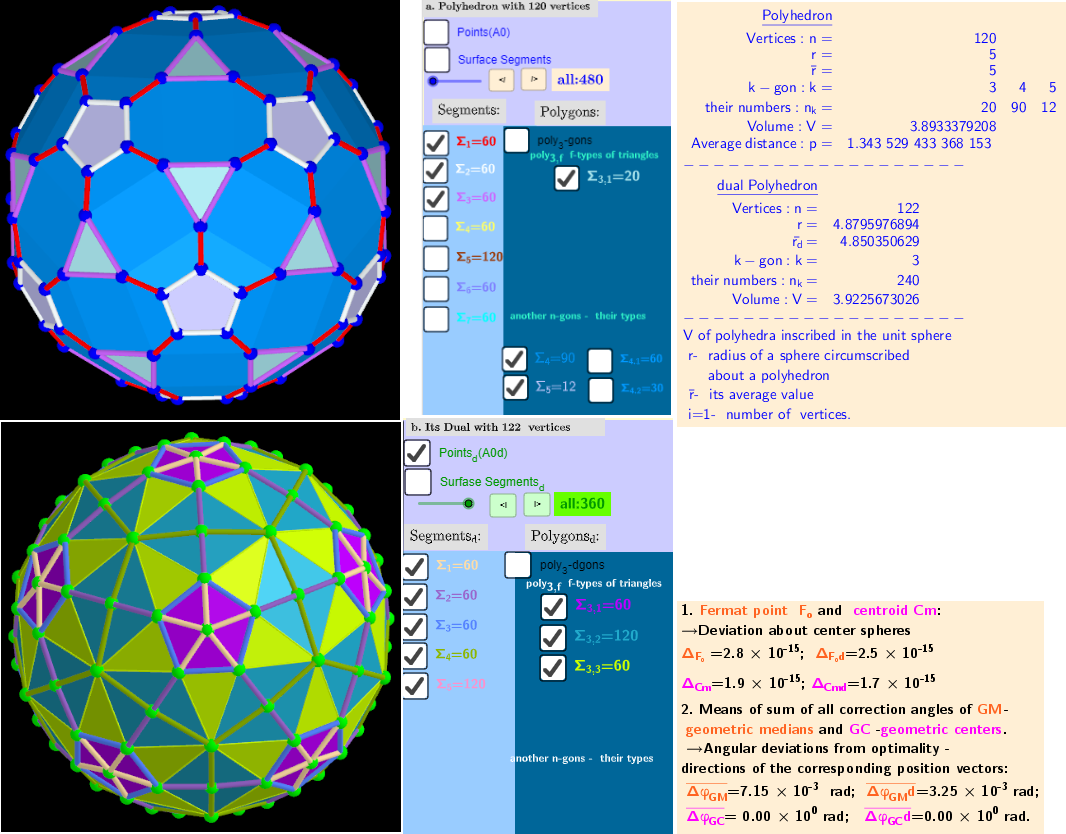
Actual location of the quadrilaterals