RUSD Math 2: Unit 2

Cindy Almazan, Sep 15, 2021

Table of Contents

  1. G.CO.2
    1. G.CO.2 Experiment with transformations in the plane
    2. G.CO.2 Experiment with Transformations in the plane
    3. G.CO.2 Dilation Introduction: Transformers!
    4. G.CO.2 Dilation Transformation Station
    5. G.CO.2 Dilation Exploration
  2. G.CO.3
    1. G.CO.3 Rotational Symmetry
    2. G.CO.3 Exploring Rotations 1
    3. G.CO.3 Exploring Rotation 2
    4. G.CO.3 Exploring Rotation 3
  3. G.CO.4
    1. G.CO.4 Exploring Translations 1
    2. G.CO.4 Exploring Translations 2
    3. G.CO.4 Exploring Translations 3
    4. G.CO.4 Exploring Translations 4
    5. G.CO.4 Exploring Translations 5
    6. G.CO.4 Exploring Translations 6
    7. G.CO.4 Experiment with Rotations on the plane
    8. G.CO.4 How to Find the Center of Rotation
  4. G.CO.5
    1. G.CO.5 Experiment with Transformations in the plane
    2. G.CO.5 Experiment with transformations in the plane 2
  5. G.CO.6
    1. G.CO.6 Sequence of Rigid Motions
    2. G.CO.6 Understand congruence in terms of rigid motions
  6. G.SRT.1
    1. G.SRT.1 Understand Similarity in terms of similarity transformations
    2. G.SRT.1 Understand similarity in terms of similarity transformations p2
  7. Performance Tasks
    1. Understand congruence and similarity using geometry software
    2. Dilations Relations
    3. Mapping Triangles

1.

G.CO.2

  • 1. G.CO.2 Experiment with transformations in the plane
  • 2. G.CO.2 Experiment with Transformations in the plane
  • 3. G.CO.2 Dilation Introduction: Transformers!
  • 4. G.CO.2 Dilation Transformation Station
  • 5. G.CO.2 Dilation Exploration

1.1.

G.CO.2 Experiment with transformations in the plane

Click on the blue translations box to begin experimenting with translations about the coordinate plane. [br]1) Move point E to (4,2)[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAABGdBTUEAALGPC/xhBQAAAAtJREFUCB1jYAACAAAFAAGNu5vzAAAAAElFTkSuQmCC[/img] and point D to (10,4[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAABGdBTUEAALGPC/xhBQAAAAtJREFUCB1jYAACAAAFAAGNu5vzAAAAAElFTkSuQmCC[/img]), to create a vector. How does △ABC[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAABGdBTUEAALGPC/xhBQAAAAtJREFUCB1jYAACAAAFAAGNu5vzAAAAAElFTkSuQmCC[/img] transform to △A′B′C′[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAABGdBTUEAALGPC/xhBQAAAAtJREFUCB1jYAACAAAFAAGNu5vzAAAAAElFTkSuQmCC[/img] as a result of this vector?
2) What do you notice about the angle measures of `△ABC` and `△A'B'C'`?
Click on the blue translations box to begin experimenting with translations about the coordinate plane.
3) How does `△ABC` transform to `△A'B'C'` given a vector?
4) What is true about the angle measures of `△ABC` and `△A'B'C'` after a translation occurs?
Click on the green reflections box to begin experimenting with reflections on the coordinate plane. [br][br]Move points D and E around the coordinate plane to see how `△ABC` is reflected about line DE.
5) What do you notice about the angle measures of `△ABC` and `△A'B'C'`?
Click on the orange rotations box to begin experimenting with rotations on the coordinate plane. [br][br]Move point E around the coordinate plane and use the rotation slider to change the angle of rotation to see how `△ABC` is rotated about point E
6) What do you notice about the angle measures of `△ABC` and `△A'B'C'`?
– pinarocj, Cindy Almazan

1.2.

–

1.3.

–

1.4.

–

1.5.

–

2.

G.CO.3

  • 1. G.CO.3 Rotational Symmetry
  • 2. G.CO.3 Exploring Rotations 1
  • 3. G.CO.3 Exploring Rotation 2
  • 4. G.CO.3 Exploring Rotation 3

2.1.

G.CO.3 Rotational Symmetry

If the polygon is mapped to itself after a rotation of between 0 and 360 degrees, the shape has rotational symmetry. [br]Which of these shapes have rotational symmetry? Which do not? For the shapes that have rotational symmetry, for what angle measure(s) does the figure map to itself?
For the triangle, describe the rotations that carry the figure onto itself.
For the rectangle, describe the rotations that carry the figure onto itself.
For the pentagon, describe the rotations that carry the figure onto itself.
– Irina Boyadzhiev, Hanover County Mathematics, Cindy Almazan

2.2.

–

2.3.

–

2.4.

–

3.

G.CO.4

  • 1. G.CO.4 Exploring Translations 1
  • 2. G.CO.4 Exploring Translations 2
  • 3. G.CO.4 Exploring Translations 3
  • 4. G.CO.4 Exploring Translations 4
  • 5. G.CO.4 Exploring Translations 5
  • 6. G.CO.4 Exploring Translations 6
  • 7. G.CO.4 Experiment with Rotations on the plane
  • 8. G.CO.4 How to Find the Center of Rotation

3.1.

G.CO.4 Exploring Translations 1

Before you start, try moving the slider (the black dot on a line directly under the word "vector") left or right. Don't worry about what a vector is for now (or [url=http://lmgtfy.com/?q=define+vector+math]google it if you must know[/url]); just have fun moving the slider. Seriously, have fun with it. Like, smile and stuff.[br][br]The brown shape doesn't move: this is called the preimage. The preimage is the shape that we will be translating (because it's "pre" translation). The pink shape is called the image, because it's the "image" of the preimage after transformation. Preimage = before transformation (brown), and image = after transformation (pink).
Question 1
a) Translate the polygon so that point A is at (5,3). How far did the polygon move from its [b]original position[/b]? [br]
[i]Check your answer, then [url=https://www.geogebra.org/book/title/id/2660003#material/2664627]go on to Exploring Translations 2.[/url][/i]
b) Now translate it so that point C is at (0,4). How far did the polygon move from [b]the last[/b] position? [br]
c) Is this a horizontal or vertical translation? Explain your reasoning.
– Cindy Almazan, Mr. Watson

3.2.

–

3.3.

–

3.4.

–

3.5.

–

3.6.

–

3.7.

–

3.8.

–

4.

G.CO.5

  • 1. G.CO.5 Experiment with Transformations in the plane
  • 2. G.CO.5 Experiment with transformations in the plane 2

4.1.

G.CO.5 Experiment with Transformations in the plane

1) Translate [math]\triangle[/math]ABC -7 units horizontally and +1 units vertically. Make this triangle green.[br][br]2) Reflect [math]\triangle[/math]ABC over the x-axis. Make this triangle red.[br][br]3) Rotate [math]\triangle[/math]ABC [math]90^0[/math]clockwise about the origin. Make this triangle blue.[br][br]4) Reflect [math]\triangle[/math]ABC over the line y=6. Make this triangle black.
– Cindy Almazan

4.2.

–

5.

G.CO.6

  • 1. G.CO.6 Sequence of Rigid Motions
  • 2. G.CO.6 Understand congruence in terms of rigid motions

5.1.

G.CO.6 Sequence of Rigid Motions

1) Is there a sequence of rigid motions that maps the blue triangle onto the red triangle? Explain how you know. [br]
2) Are the 2 triangles congruent? Explain your reasoning.
– Mr Hardin, Cindy Almazan

5.2.

–

6.

G.SRT.1

  • 1. G.SRT.1 Understand Similarity in terms of similarity transformations
  • 2. G.SRT.1 Understand similarity in terms of similarity transformations p2

6.1.

G.SRT.1 Understand Similarity in terms of similarity transformations

Perform a dilation from the origin using the following function rule f(x, y) → (3x, 3y).
a) What is the scale factor of the dilation?
b) Using ΔABC and its image ΔA’B’C’, connect the corresponding pre-image and image points. Describe how the corresponding sides are related.
c) Determine the length of each side of the triangle. How do the side lengths compare? How is this comparison related to the scale factor?
d) Determine the distance between the origin and point A and the distance between the origin and point A’. Do the same for the other two vertices. What do you notice?
– Cindy Almazan

6.2.

–

7.

Performance Tasks

  • 1. Understand congruence and similarity using geometry software
  • 2. Dilations Relations
  • 3. Mapping Triangles

7.1.

Understand congruence and similarity using geometry software

The core elements of performance required by this task are:[br]Geometry 8.G[br]Understand congruence and similarity using physical models, transparencies, or geometry software.[br]1. Verify experimentally the properties of rotations, reflections, and translations.[br]a. Lines are taken to lines, and line segments to line segments of the same length.[br]b. Angles are taken to angles of the same measure.[br]c. Parallel lines are taken to parallel lines.[br][br]2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.[br][br]3. Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
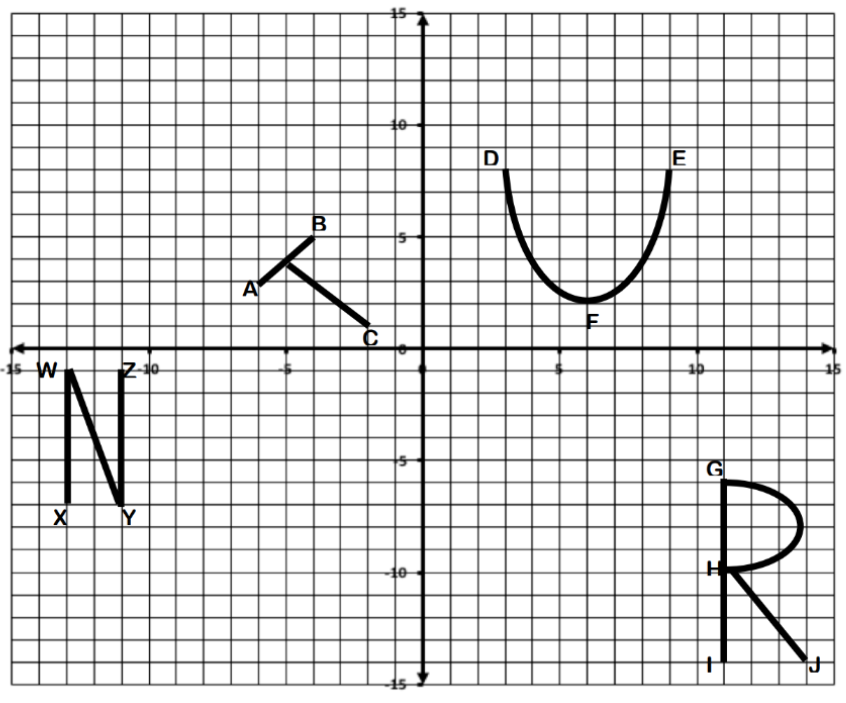
Crosby has drawn the letters [b]T[/b], [b]U[/b], [b]R[/b], [b]N[/b] on the coordinate plane below and labeled points on each of the figures with other letters
Write the coordinate pair for each point labeled on the letter [b]T[/b] on the graph.[br]A:[br]B:[br]C:
Crosby reflects the letter [b]N[/b] across the x-axis. Draw the new image after the reflection on the coordinate axis below.
List the coordinates of the four endpoints of the new image of the N after the reflection.[br]W':[br]X':[br]Y':[br]Z':
Crosby rotates the letter [b]T[/b], 180 degrees about the origin.[br][br]Draw the rotated image on the coordinate axis and label the corresponding points with A', B', and C'.
Crosby wants to duplicate that same transformation of starting with the original [b]T[/b] and covering the new image you drew, but his time he uses reflections. Explain the transformations he must use.
Crosby wants to use a series of reflections to move the letter [b]R[/b] around the coordinate plane.
How many reflections would he need to make to end up covering the original pre-image of the [b]R[/b]? Explain how you know.
Crosby thinks he can always duplicate any [math]180^o[/math]rotation of a pre-image to image by also using a single reflection of the two figures.
Do you agree or disagree with Crosby? Use mathematics to explain your answer.
– Cindy Almazan

7.2.

–

7.3.

–

Information