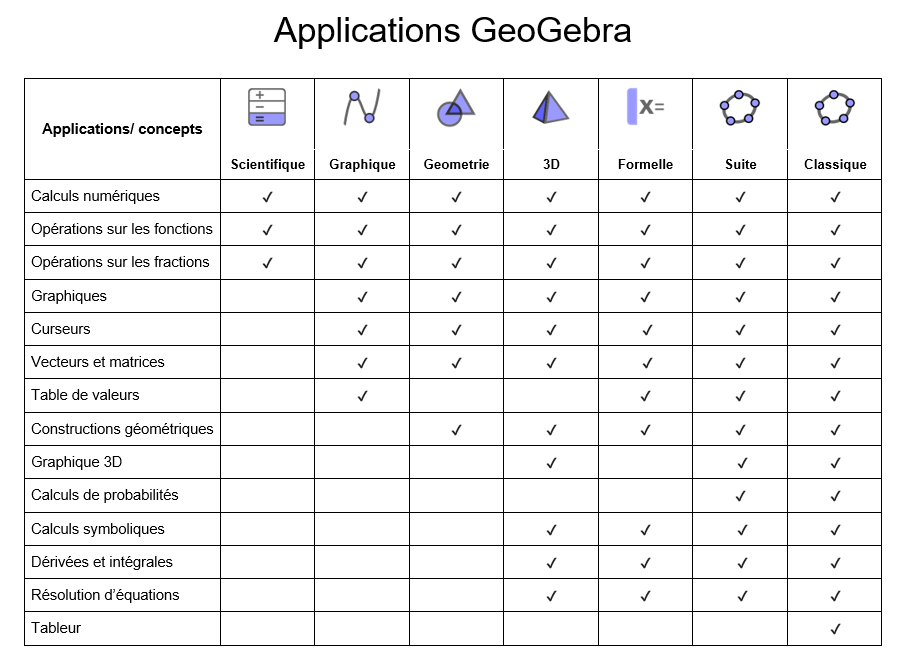
Avec nos applications mathématiques GeoGebra, vous pouvez explorer et apprendre les fonctions, la géométrie, l'algèbre, les statistiques et la 3D de façon nouvelle et interactive.[br][list][*][url=https://www.geogebra.org/scientific]Calculatrice scientifique[/url][/*][*][url=https://www.geogebra.org/graphing]Calculatrice graphique[/url][/*][*][url=https://www.geogebra.org/geometry]Géométrie[/url][/*][*][url=https://www.geogebra.org/calculator]Suite Calculatrice[/url][/*][*][url=https://www.geogebra.org/cas][/url][url=https://www.geogebra.org/cas][/url][url=https://www.geogebra.org/cas][/url][url=https://www.geogebra.org/cas][/url][url=https://www.geogebra.org/cas][/url][url=https://www.geogebra.org/cas]Calculatrice formelle[/url][br][/*][*][url=https://www.geogebra.org/3d]Calculatrice 3D[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classique[/url][br][/*][/list]L'application qui vous convient est celle qui répond à vos propres besoins et qui, si elle est utilisée dans les tests, répond aux règlements d'examen de votre région. Le tableau suivant donne un aperçu des fonctionnalités disponibles dans les différentes applications.[br][br]Ces applications sont accessibles en ligne, sur le site, mais peuvent également être installées sur un appareil mobile pour utilisation hors ligne. Les applications [i]Calculatrice Suite[/i], [i]Calculatrice Graphique[/i], [i]GeoGebra Classique[/i] (versions 5 et 6), [i]Calculatrice 3D,[/i] [i]Géométrie [/i]et [i]Calculatrice Formelle[/i] peuvent également être installées sur un ordinateur pour utilisation hors-ligne. [url=https://www.geogebra.org/download]Lien pour les téléchargement[/url].

Nous pensons que les élèves ont intérêt à utiliser exactement la même application GeoGebra en classe, à la maison et pendant les tests. De cette façon, ils obtiendront le plus de pratique avec l'application et seront donc en mesure de faire le meilleur usage de notre technologie dans toutes les situations. C'est pourquoi nous avons créé notre mode d'examen GeoGebra et l'avons ajouté dans chacune de nos applications. Le mode examen verrouille les appareils mobiles afin que les étudiants ne puissent pas communiquer ou utiliser d'autres applications que GeoGebra pendant un test. Cette approche a déjà été testée sur le terrain et approuvée par plusieurs ministères de l'éducation dans plusieurs régions. [url=https://www.geogebra.org/m/tj6xg3ja]En savoir plus sur l'utilisation de GeoGebra dans les examens.[/url][br][br]

Créer une fonction linéaire avec des curseurs et la recouper avec une fonction quadratique afin d'afficher le ou les points d'intersection.[br][br]Explorez la construction et apprenez comment créer une fonction avec des paramètres et comment recouper deux fonctions avec l'application [i]Calculatrice Graphique[/i] de la [i][url=https://www.geogebra.org/calculator]Calculatrice Suite[/url][/i] de [i]GeoGebra[/i]. Puis essayez-le vous-même en suivant les instructions ci-dessous.

[table][tr][td]1.[br][br][/td][td][/td][td]Entrez la fonction linéaire [math]f(x)=a\cdot x+b[/math] dans le [i]champ de saisie[/i] de la fenêtre [i]Algèbre[/i]. Les curseur des paramètres [i]a[/i] et [i]b[/i] sont créés automatiquement.[/td][/tr][tr][td]2.[br][br][/td][td][/td][td]Activez le [i]bouton de visibilité [/i][img]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/16px-Algebra_hidden.svg.png[/img] à côté des curseurs afin de les afficher dans la[i] fenêtre Graphique.[/i][br][/td][/tr][tr][td]3.[/td][td][/td][td]Modifiez la valeur des paramètres [i]a et[/i] [i]b [/i]et observez l'effet sur la représentation graphique de [i]f(x).[/i][br][/td][/tr][tr][td]4.[/td][td][/td][td]Créez une fonction quadratique en saisissant [math]g\left(x\right)=x^2[/math] dans le [i]champ de saisie[/i] de la f[i]enêtre Algèbre[/i].[/td][/tr][tr][td]5.[br][br][br][/td][td][/td][td]Utilisez la commande [math]Intersection\left(f,g\right)[/math] pour créer les points d'intersection des fonctions [i]f(x) [/i]et [i]g(x). [/i]Les points d'intersection [i]A [/i]et [i]B[/i] sont affichés dans la [i]fenêtre Graphique,[/i] tandis que les coordonnées des points sont affichées dans la [i]fenêtre Algèbre[/i].[/td][/tr][tr][td][/td][td][icon]/images/ggb/toolbar/mode_intersect.png[/icon][/td][td][b]Remarque:[/b] Vous pouvez également utiliser l'outil [i]Intersection [/i]que vous trouverez dans la fenêtre des [i]Outils[/i]. Sélectionnez l'outil puis cliquez sur la représentation graphique de chaque fonction afin de créer les points d'intersection.[/td][/tr][tr][td]6.[br][br][/td][td][/td][td]Faites varier la valeur des paramètres [i]a et[/i] [i]b [/i]et observez comment les points d'intersection [i][b]A [/b][/i]et [i][b]B [/b][/i]s'adaptent aux changements.[/td][/tr][tr][td]7.[/td][td][img width=24,height=24]https://lh5.googleusercontent.com/EeYLvel9HmsnYD7ZRVm-HBQtblHhlB35cdQzXdG11nyuG3R7BCgnyC_l3L8aKn1R4wNkQnlMJHA72jcGN8n5f2RRahLZMiuy01yMfDJFEssc0gxkkfajbgHSyt1KTilGP0RyH5NA[/img][/td][td]Modifiez la couleur du graphique des fonctions [i]f(x) [/i]et [i]g(x) [/i]avec la [i]barre de style [/i]afin d'améliorer ou de personnaliser votre construction.[/td][/tr][/table]

Déterminer un nombre complexe et changer ses coordonnées cartésiennes en coordonnées polaires.[br][br]D'abord, observez la construction ci-dessous pour apprendre à visualiser les nombres complexes sur une grille de coordonnées polaires puis refaites cette construction avec l'application [i]Calc Graphique[/i] de la [url=https://www.geogebra.org/calculator]Calculatrice Graphique Suite[/url] de [i]GeoGebra [/i]en suivant les instructions plus bas sur cette page.

[table][tr][td]1.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/1/18/Algebra_new.svg/32px-Algebra_new.svg.png[/img][/td][td]Dans la fenêtre [i]Algèbre[/i], ouvrez l'aide à la saisie et sélectionnez [i]Texte[/i].[/td][/tr][tr][td]2.[/td][td][/td][td]Copiez le texte suivant dans le [i]champ de saisie[/i] et faites [i]Entrée[/i].[/td][/tr][tr][td][/td][td][/td][td][i]CCSS.MATH.CONTENT.HSN.CNB.4[br]Représenter les nombres complexes sur le plan complexe sous forme rectangulaire et polaire (y compris les nombres réels et imaginaires), et expliquer pourquoi la forme rectangulaire et polaire d'un nombre complexe donné représente le même nombre.[/i][/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_complexnumber.png[/icon][/td][td]Ouvrez la [i]fenêtre Outils[/i], sélectionnez l'outil [i]Nombre complexe[/i] et cliquez n'importe où dans la [i]fenêtre Graphique[/i] pour créer un nombre complexe.[br][b]Remarque:[/b] Le nombre complexe sera automatiquement étiqueté z[sub]1[/sub] et ses coordonnées seront affichées dans la [i]fenêtre Algèbre[/i].[br][/td][/tr][tr][td]4.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Ouvrez le menu des [i]Propriétés globales[/i] et modifiez la taille des caractères.[/td][/tr][tr][td]5.[/td][td][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/2/25/Stylingbar_caption.svg/16px-Stylingbar_caption.svg.png[/img][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/b/bd/Stylingbar_point.svg/16px-Stylingbar_point.svg.png[/img][/td][td]Sélectionnez le nombre complexe dans la [i]fenêtre Graphique[/i], ouvrez la [i]barre de style[/i] afin d'afficher sa valeur et la taille du point.[br][b]Remarque:[/b] Dans l'application mobile, dans la [i]barre de style[/i], cliquez sur les trois points pour afficher les paramètres, cliquez ensuite sur [i]Légende [/i]puis sélectionnez [i]Valeur[/i].[/td][/tr][tr][td]6.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/32px-Algebra_hidden.svg.png[/img][/td][td]Entrez [math]z_2=z_1[/math] dans le [i]champ de saisie[/i], appuyez sur [i]Entrée[/i]. Masquez ensuite ce nouveau nombre en cliquant sur le [i]bouton de visibilité[/i] à sa gauche.[/td][/tr][tr][td]7.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img][/td][td]Dans la [i]fenêtre Algèbre[/i], ouvrez le menu contextuel de z[sub]2[/sub] et sélectionnez [i]Propriétés[/i]. Dans la [i]fenêtre des propriétés[/i], ouvrez l'onglet [i]Algèbre[/i], puis changez les [i]Coordonnées [/i]pour [i]Coordonnées polaires [/i]et fermez la fenêtre des propriétés. Dans la [i]fenêtre Algèbre,[/i] le nombre z[sub]2[/sub] sera maintenant affiché en coordonnées polaires.[br][b]Note: [/b]Dans l'application mobile, écrivez [math]z_2=EnPolaires(z_1)[/math] afin d'afficher ses coordonnées polaires dans la [i]fenêtre Algèbre[/i].[/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Déplacez le point [i]z[sub]1[/sub][/i] dans la [i]fenêtre Graphique[/i] et observez comment les valeurs des deux nombres complexes varient.[/td][/tr][tr][td]9.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Ouvrez les [i]propriétés[/i], déroulez le menu de [i]Affichez Grille[/i], sélectionnez [i]Polaire[/i].[br][b]Remarque:[/b][i] [/i]Dans l'application Mobile, cliquez sur le menu de [i]Type Grille[/i] et sélectionnez [i]Polaire[/i].[br][/td][/tr][/table]