[size=100][justify][color=#666666]A tömege vagy a súlya alapján lenne érdemes eladni Norvégiában, illetve Egyiptomban a Budapesten vásárolt aranytömböt?[br]   [br][/color][/justify][/size]

[color=#666666][size=100][justify]A szimuláció segítségével megvizsgálhatod a nehézségi erő helytől való függését.[/justify][/size][/color]

[size=100][justify][color=#666666]Azonosítsd be a testre ható erőket![br][br]a) Mit látsz, milyen erők hatnak a Földön egy nyugvó testre?[br][br]b) Mit nevezünk tömegvonzási (gravitációs) erőnek? Milyen irányú ez az erő?[br][br]c) Milyen irányú a Föld forgásából származó centrifugális erő?[br][br]d) Mit nevezünk nehézségi erőnek? Mit mutat a vektorábra?[br][br]e) Mozgasd a testet és figyeld meg az erővektorok nagyságát! Azonos a testre ható nehézségi erő és a tömegvonzási erő? Miért?[/color][/justify][/size]

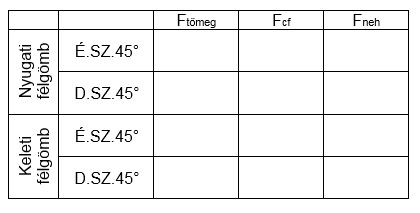
[size=100][justify][color=#666666]Az animációban milyen adat jellemzi a test helyét? [br][br]a) Ez az adat egyértelműen elegendő egy test helyének meghatározásához a Földön?[br][br][/color][color=#666666]b) Az animációban a test helyét változtatva állítsd be a táblázatbeli pozíciókat és az egyes mennyiségek értékeit leolvasva töltsd ki az alábbi táblázatot![br][/color][/justify][/size][justify][/justify]

[size=100][justify][color=#666666]Mozgasd a testet, figyeld meg a testre ható erőket, és válaszolj a következő kérdésekre![br][br]a) Mit mondhatunk a tömegvonzási erő nagyságáról?[br][br][/color][color=#666666]b) Hol a legkisebb a centrifugális erő nagysága és mekkora az értéke? [/color][color=#666666]Mit mondhatunk ekkor a testre ható másik két erőről? Add is meg az értéküket![br][br]c) Hol a legnagyobb a centrifugális erő nagysága és mekkora az értéke? Mit mondhatunk ekkor a testre ható nehézségi erőről?[br][br]d) Hogyan változik a centrifugális erő a szélességi körök mentén? Miért?[br][br]e) Hogyan és miért változik a nehézségi erő a szélességi körök mentén? Add meg az értékét a sarkoknál és az Egyenlítőnél![/color][/justify][/size]

[size=100][color=#666666]A testekre ható nehézségi erő a földi tömegvonzási erő és a Föld forgásából adódó centrifugális erő eredője:  [br][/color][br][color=#666666][math]\vec{F}_{neh}=\vec{F}_{tömeg}+\vec{F}_{cf}[/math][/color][br][color=#666666][br][br][u]A tömegvonzási erő[/u]:[br] [math]F_{tömeg}=γ\frac{M\cdot m}{R^2}=9,8258[/math] [math]N[/math][br][br]ahol [br][math]M=5,97\cdot10^{24}[/math] [math]kg[/math] a Föld tömege, [br][math]m=1[/math] [math]kg[/math] a test tömege,[br][math]γ=6,67\cdot10^{-11}[/math] [math]Nm^2/kg^2[/math] a tömegvonzási állandó, [br][math]R=6366[/math] [math]km[/math] a Föld átlagos sugara. A centrifugális erőt figyelembe véve a Földet gömb alakúnak tekintjük.[b] [br][/b][br][br][u][br]A centrifugális erő[/u]:[br][math]F_{cf}=m\cdot r \cdot \vec{ω}^2[/math][br]ahol[br][math]m=1[/math] [math]kg[/math] a test tömege, [br][math]r=Rcosφ=6366cosφ[/math] [math]km[/math] az adott pont távolsága a Föld forgástengelyétől.[br][math]\phi[/math] a test helyéhez tartozó szélességi fok.  [br][br][math]ω=\frac{2π}{T}=\frac{2π}{24 \cdot 3600 s}=7,29 \cdot 10^{-5} \frac{1}{s}[/math] a Föld szögsebessége.  [br][br][br][/color][/size][size=100][color=#666666]Az itt leírt számítás egy olyan modellt alkalmaz, amely a Föld teljes tömegét a Föld középpontjában képzeli el. Ezzel a modellel természetesen nem kaphatjuk meg a valódi, mérésekkel kapott nehézségi erőt, hiszen ahhoz a Föld valódi tömegeloszlását is figyelembe kellene venni.[br][/color][/size][br][size=100][color=#666666][br][/color][/size]