Understand congruence and similarity using geometry software
The core elements of performance required by this task are:[br]Geometry 8.G[br]Understand congruence and similarity using physical models, transparencies, or geometry software.[br]1. Verify experimentally the properties of rotations, reflections, and translations.[br]a. Lines are taken to lines, and line segments to line segments of the same length.[br]b. Angles are taken to angles of the same measure.[br]c. Parallel lines are taken to parallel lines.[br][br]2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.[br][br]3. Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
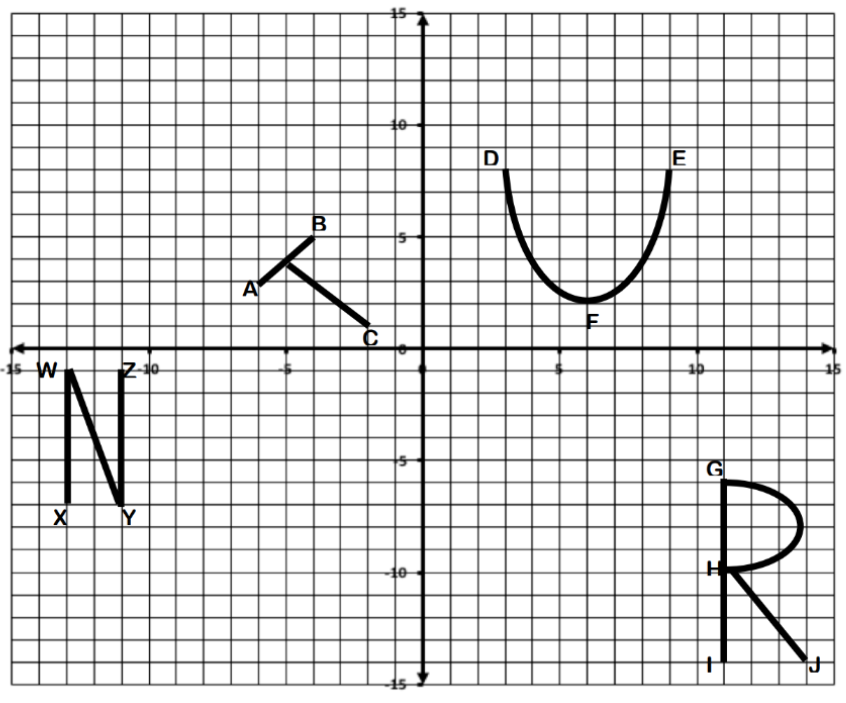
Crosby has drawn the letters [b]T[/b], [b]U[/b], [b]R[/b], [b]N[/b] on the coordinate plane below and labeled points on each of the figures with other letters

Write the coordinate pair for each point labeled on the letter [b]T[/b] on the graph.[br]A:[br]B:[br]C:
Crosby reflects the letter [b]N[/b] across the x-axis. Draw the new image after the reflection on the coordinate axis below.
List the coordinates of the four endpoints of the new image of the N after the reflection.[br]W':[br]X':[br]Y':[br]Z':
Crosby rotates the letter [b]T[/b], 180 degrees about the origin.[br][br]Draw the rotated image on the coordinate axis and label the corresponding points with A', B', and C'.
Crosby wants to duplicate that same transformation of starting with the original [b]T[/b] and covering the new image you drew, but his time he uses reflections. Explain the transformations he must use.
Crosby wants to use a series of reflections to move the letter [b]R[/b] around the coordinate plane.
How many reflections would he need to make to end up covering the original pre-image of the [b]R[/b]? Explain how you know.
Crosby thinks he can always duplicate any [math]180^o[/math]rotation of a pre-image to image by also using a single reflection of the two figures.
Do you agree or disagree with Crosby? Use mathematics to explain your answer.