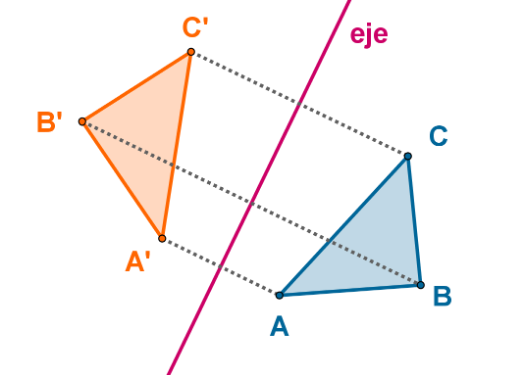
Dada una recta [i]e,[/i] se llama [b]simetría axial de eje [i]e[/i][/b] a un movimiento que hace corresponder a cada punto P otro punto P' tal que la recta [i]e[/i] es la mediatriz del segmento PP'.[br]A la recta [i]e[/i] se le llama [b]eje de [/b][b]simetría[/b].[br][br]

Las simetrías axiales son transformaciones que conservan la forma y el tamaño, es decir, son movimientos. Pero no conservan la orientación, por lo que se trata de movimientos inversos.[br][br]

Observar las siguientes imágenes:

[size=85][size=100]Es un software gratuito de matemáticas que ofrece la posibilidad de asociar objetos geométricos y algebraicos para resolver problemas complejos. El software permite abordar diferentes problemas matemáticos de forma creativa y original. [br]En esta clase utilizaremos esté soffware para poder realizar de manera más dinámica los paso a seguir para obtener el simétrico de algún objeto respecto a un eje de simetría.[/size][/size]

En esté ejemplo se muestra como debemos realizar la simetría axial de una figura paso a paso sin utilizar la herramienta de simetría axial.

En el siguiente applet aparece una recta e que es el eje de simetría de las simetrías axiales que apliques.Utilizando las siguientes herramientas:[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAyCAYAAAFtzWgaAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAAsiSURBVFhHzZl5UJXXFcCff3fajjPJTNvkn4xJJ/mjJradtKaGOqZq21QztWm1NmkbY5TUJZ00Oo6NU8AF1GhUFNy3uEAEtRAUEAIIiOw7jx1kE5FVUNlP7+9+73u8x3ssCm09M2e+9+537z3n3LPfz9Le3i7uUL9ISUmR1NRU/QSTkpKMF8C6997WT6CsrGzoRXt1sdwtyhBrxBfOLxi8vnWl/l1RUTH0YjhYOjo65ODBgy6oV7hD/cJk08Te3l6xNDc36z2TdqzRT+DBgwdiqa2t1X/gqrU8XyIiLklbW5tYiouLZXCgX1rKcvUEoKGhQSy5ubmyf7+/bciAW7duieXQoUMurB47dsyQY7ygSSBGa2urHmhraxGLJVj/Hg6ca3d3t7Hg7t27tmGRJmumligtYJNtxAAW3L9/31hQUlKiBwcHB6SlJEcvMPHNGS8pqq9qBd2+fdtYUFBQoBdYLIclcvta/Xs41NTUSF1dnbEgMzNT8vLyRsX9+/cPmcGjoGXv3r02omPDNl9fsWRnZ0t1dbW2CkeDHo5dXV3i4+NjLLBarXoHi2WpbNz4kf49HO7du2csyMrKksLCQj0YfflLqQw/po1oOMC/y4I0/w367FtKcyTv7G49ZgImqRdwpDk5OXowwed9J6VFrfudeHkbLKI0vSAjI0PS09P1YPbxbfbJzcVZUn3ltJIrWu7cadQ6sC9IS0vTC/LP75O7ypZu7l0nbVXGQZhQXl4umzdvNhbcvHlTvL3VasuvpL/7gW2KM9gXwA7nPDAwIHFxsbbXzhAeHi7BwcEGSyxwZzuOiL8WFRUZCxITE11ccSTs7Ow0XBQ9XLp0SS5evDhpGBERMeRwRA4IYS5QnQhio+zT399viAwB7BVLMW3WhOzsTAkNDbL9Gx9gDxDq6elxJkBgciTQ3Nyk1L5SYYIs+/0bttGxgViEBAQwOwH8gUBm+oQJFdFBUpPwb221t7MTJdxzjnTdrrG9dQ8Q4DQ4fycJmpqa7LHMhHjvZdJ+q8TJn1pKc6U88rxc27BYzRg0JjoABDgNJwJ4Q2lpqX46Qsrn/5DWigInAo7YXV8u8z3mqGPsUvhnlQhuaY+prKyUxsZGZwIYu+mjwGB/n+Sd2a191dywuThb7hSkivXiIQlbMVs6G6plQFlLQkK02rBBr0PJECHraNc0CeBJhEgTgoNOScwRP2lXEsRsXCLpgZv0hmMBBDgNUoKTBPn5+TpoAKtWfaRETlS4TIlrJKWxgE1DQ0Pl7NmzQuK9fv26bNmyxSBAvEDRHBFEQAIn4+b/8eC5c+ckLCxMR4WqqirjiMyqBK2j/YkiDLe0tKggfGfoiP6baMHjrl69qs/PXdB6XOSICRmWff7+WkGTDcdPnNAFhmXbtm16AF0QCR0j4+Mie5E18Qc7ATan3jVLA6wCv+Bpjo0HqbUgUF9fP0RgcHBQEyB9OUJIyDmprR09uA0HzB3lOhEgwSKaI4HXX5+pHC1KpkyZaRsZH5i5ZUwCM2f+WBFIVzhdRMWl8YKZW5wIkN44N0cCEPV8y0Myvr4qX62aK425ybY3owO5hT6AWGQn0NfXp89tuA4yA/8prWV5qjDOlZxT2yXrmGEQo4GZvMZH4IiPPVw3l2RLTbKS5sM3pKdr5GbBLQH6GxQznECWQ7FnYmtlkSTvXCMlYSdss5wBDyY7OhEg0OEYjgT6VI2Xc3K7CwGwpTRPCi8ESuqO1SpvnBYvr7WKScMQiMi0XHixnQDck+bICSY0FaZL6Ven3BIwMSsuTOcMi+WhLF++Sq/D2cjL1Pl2ApgVmciRgPXSEam7ec3txuTpWqWPK75r1ObzFF6T9es/1utu3LihvdmJAPGbP44EEn0/1Iod2jhT52TKlyur50thSKAqle/rXBwfH6XNGoAA+X1MAtfWv23vsiFUlxojYR94SGXMBenv7bbNcgW3BHAMQrZJoL6+QTYufEU6a8qkROkh8u8LpEJtPB5ITk7WBQQp004As4IqBLqUjVssLysMl4U//aFUxYbYlo4PiL7owIUAdSkEWlupSRcoLJTFi1fYlo0ORGMSfkxMjBw5ckR2797tTIAEjVhm6ZiamiI7d+6Qhw8f6v/jAeyfYgt/OnPmjCaAZWoCDMI9tQwiMhmPNBPOeJAS54RKk0jCXviVnQCUaULw5MdFNqWroUEjZNsJ7Nq1S9+DYKqO9c3jIBEBJLcEBQVpU9Vly/Hjx10auIliZGSkTsP2wouLIaIqoftJRnjE+Ey+LbRTWCh3Kn5+fhIYGPhEIyaz87PPtNGibq0BGCdEAUg3Gd3yZCM8YSXEDOIDjYF2AgTA0/AMgP/ULzxxjCcBOWmTJ0yIgovGQwc6dwJQAJgdp+mZjshmnEpXl4GcDuvczZ0oEoK4/8JhoTuqAKiHRUwmNRD73MHJkydl1qx5Mm3an+T55+fL0qVLlU0OtdeTCRQn8MaBwSv3KyMKQE1APGQyAiD9cKioKFGMP6Ny3WWFXFSCf5N3/rLANmNywRQALcMbYXlUAbA5MzK5EwAICDggL//gNfnmN96Uqd+eLa+98pLsWf4bKQ0NlI66CtusyQFTAMwH3ggybgWg3KYBoTZiMpdSIwkAcHGbdmCDKi0PS3tVkbSV56uy/oq+W6K0r4q/LD333H/seBRAAHiDT3gjEpkXLC4CkCjoGRgbSwDagszD3lJ7I2roi4DqUbgIaypIk9KIL5Qw7+nKszE7SQbV4TwOmALgm/BGgHErAGrCw6ntmEzpNZoASdtXq25thzp9q0PdPYRcH7aW5UtjTrKuv6PXLTLqdFWXPwogAJUZ9g9vowrwKBqI8/qrZB3d7HIV6R4zlaDF0pARLxkH/yVRnyyS9IBPpaN2bH8xBTA1MKIJcVeHlPQGlHqkakpAd4CjJvmtUs1fgLSpTtM90yOgMjO+MNQpf0ncukJ8Fv1EnvneDBXJfqHxxRd/psrOMBVtjGIbJun14AlhqJ2pEkcUgH6BFD2yAIO6B+dTR3l0kP4Y6JbREVCbVnmB9NaXS+Tpz2Xad7+vGPe1hWNwq2pFPBXDxtU5vFDm8IS3CQvAZ7z8IH/JPuEr9elxLp/0hiM231KWpxw7VerSYrTWYje9I1EfvyVFwfskLuyC/Hz2HHn66Wflqaeelblz5+mkSFIFHkkA4iwlBC8oI9wK0N+nQyV3By7mo8yj2Zqlkf/16V8rQf3k6tpfS7zP+zoytXD69zttu40NpgDwBG90RwhAMeciAHGWDIyt0Y+N5AMJny4R65f+0lFtOLC+Q1IRpzI2VNn1SuWkv5XMQ15SduWMPv2JAALQa8MTvJHEaCjdagAvJ/qgKhpFRwGs1kJ5990/ygsv/FK+861XZZ6Hh5zdvk7S9q6XxC0fSMqeT6T48lF50NxoWzE5gADcrnL68MbNEAK41QBxlvjPZEcB6uurZOHCP8iUKV4OznZUPGYtlqzcoU8YkwFUAVwD8EGGJxGIjwN07AkJCfZbDxcBcFoWUIEyiYWmADhUbGy0TJ8+QznaEpk6dZk899yPJDj4tH4/mYAfBgQE6M8mHCp8kaP4z+cTfpsCoB0nAfBwJsA4joMwZGeQOqmvr1dlQnqAe2qsR4+Z7ycLSaaU8+fPnxe+8lJgcvIHDhzQfskNxJgCkIFhngzI+P8aoUv9gyY8PT31LYTJE8yT1JwE8PX11SdOGY2joDo2+X8iAiAMvkhIhyeEMG8SiUJaAJiGebSwZ88eCQkJET498XyS0OSJz4ne3t4SFRWlhdEaAKnyaBZAup4nFeGPgo5o1d7eLv8Bw/D5Ea7mwFMAAAAASUVORK5CYII=[/img]Dibujar un polígono.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAzCAYAAAGmkbu/AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAArDSURBVFhHzVnZb5vHEedDH/LS9iEvQYH6xWlR9D9IgAZ9LJIXBw6SoDkcuHEKH7JjB1UQ2LEdH/Ftp44PWZYi+b5kSZYPRbJOS6JIkdRFkZJ4ihQl6iAlXrpl/TqzXB0kP1JH5MY/YPDtt9+3OzO7O7szs6pAIAAlUg0M+tDcZo6hrt7+6IdZnDhxXDz1LcbYD0hPF486Q0vsh0PHjmFmZgaV2qa4FhItLa1ILpVSJZNqIDQWFdPRNSeu3uyAyjMUEf1u3bpVPBk6/tDWMyxf56E12aFS2wfES2BoCOXFxaJc30Yfyswe8SLw7rsIBoOoM9IHJYn4o2p4eBh1rZYl0eYj2dER6QuOSh4SGzfKwjwaW9uiWnCDbqniLA4ePIArmRnyLQqeobkGGmdUwxicOSMLQEdbG+pbzFGtuUFVpxd3cnKQe/48gqTcHCYnZQEoqzfQaNiiDXiofja6U1KR3oraVmqgNHypSLXlaLbiECZQiwU8BSqT3QOnxzu3MpIRr6JBn58WBzXQN7dI1ZKD52quQUNjs6yO4pXfrJWleXiGwtEGRoUGKtVfZGke3bMNWmzdqNU1yurkMNK6Fg0aLW5UaQyyegGmpmQBuEuTqnEMzDeojGtgt1hQs2YNJsbHZQ3ABiIaGDrdqNa14PP169FuNMrPhNu3ZSGKaktftIGeGpTWNshqZZjNZuTVtkQb6DpcimtnIRUZLChv90QbsNkprZlkJBbfchsthWb7FOZgcvZgKDIBf3h8VYj7MnQ4oyoLBrSaBsJjqdfs3r2ykBq8t7Ah8PY5x4DXtzcwAl1TCgZ6PabUavmSHIZWY7SvhQzYHngji7eJhXjttc/JRoA1a9bLGmXwZsd2k8CgyxeG1pCcgQCtP1RXyxdlNDS3wukLxTJosrrR0DWIKq2CzcWDjsFUqGpogtY5CA0dSHMM2D7Z9uJtVBE9PWTdd9Hd1QXNs2c4/d13+Pf776O2vFx85vOX++Itfo4B23ONtQ/l9XrxE2OcDH/Y70fGyZP45O23cePyZQx4vbTz09Z/9qz8KxEVmkbRFx8JMQwqO3rFxx63W/6aAn19ADFciIyMDJSTFoVFj7D76GnUmxbMAW8wT00eVDZbUao2LI2Mlpj3p5omnD6fibPZ12hf6aWTRA4RHyVfHL6MCkM7yvXmX0jcBxH19cXhzOgxFb+HrDa9eAYvYidlmttNL94txpVHNVC3WhOP+xWQ2mhF9oMqZN0vRYiYqNKO54pl5lPYdldC3A9jx8kriIRDUG07loPx6Rn4RiYUfRBBNgea2zuVvy2gFpNZ9DM5A2w/kRvLYGh0Ci5nl+CegIICcvM65Ety2GxWDI1NJTIYFRpMwmG3y18VcOWKLCSHxdIJ3+gkJp4zgwVDNDL1HIN0zKVk8P33spAczGCQhohHZMdCBuGJafSFxpMyGBmJ4Lev/BGvvvon8pjmXaZ4WIlBH00yCxzDIEQMelMwyM3NpNOMAidVGe3U0VWnBGbgJQaR5TIIhYL43e//jDV/+CvGxsZkbSKSMgiMT6E7MJZ6DhiLnGZWciI9wTGEJuMYsPTt/WE4HYswOHhQFpRhs1rQMRBBf2QyloFjaBSG7mF0LcagsxMoKpIviXCQHRi6A3DRaMQwsPtHoHcPocvpkL+mwJYtsjCPMO05xWSMj/PvR/sZHo1lYPONoMG1RAZ0Ho/Red1qMIhwbSdFjse//Vac4U67TfTjpBFJYKBNwWCa1j57EeVPniD/rbew7+uv4fV4EmzCTnPA/SQw6BwIQ+30wd3llL+S2qEQGuvrse3jj7Fn2zZ0mkwi3kZ3N3DjhvwrFsyA+7H5IvMM0ohBe38INfZBqKursItU3pOWBi35PG7nPMMYfPCBLMTCYaNYx+6DZTCOgbkviGe2ARi0GvnrIrhwQRai6CFnLIfmo7CwEOcuXUZtmzWWgbE3gEoKkrpdSbbreFRWsnnLlygKeEsn/Ehui4XmNIZBa08AFR1elJHjtdDXSUq6VpRqmmPqHj9rQDpNfnGTnUYktIABHZkOfwTFrYsHa6mopK0beXVGUXYNkQYnr0YZ8KGf+aB61Rwv7udCfgWyZw/9F+62xH9YbZpjwOrwvv/SU9yIq3hHYMrKf4r//PcGvjp9DTtPXcWul4hYHpYrneS7WlSB0UhYKCMU4BBh85Es3CpRY2R8QtgieU0vHTHCo+PIeViNtOM5IrQJs5Vx/MT7tdnZQ+7YjMgB+MJj5EdOkicwjeFfkZg/y8HysFxTpEljh1P4pKyA2CZmFeBkCLt7nBBh57WRovV6dR35u+1Lp5s30XHjOjoMeuXvy6S6uho0G01CHlaAHWpOsCgqwMmWMVKgPzQKPznZnNVZ1AeLB8XswuGgY3s1wH40Z4b8NAv9wVHhsHP6g512RQXYH+YsDzvxnDVatgKMo0eBH34AbaSyYuVgBTjzxMEAy8UrhBXgY+yFKTDkduHphn8iZ8tGqJt0wtBWimUrwBEOX39wlMNpteUq8OjRA6xd+zcKUC4R9RHtx5tvroNWWyv/WB44zuDUHEdLnAfnAU6qAKfrOMDhnCCHCStR4MmTh3j99b+T4KeInERf4Y03/kEK1Mk/lodZBThY4vwiB0wpFQhSAOXyh0Xww3nHlSwhv9+HmtoylKZvRsPmf2FkCWF7MnAgpqPdsId2oC4/HbgUkKVWYGIKbnLteoI0AytUYA4cgh44AJw6JSuWj1kFekkBFyuQagY4Ievwj0JLQYPeTR621rB4ILgY6FwAhVQiUFkBOIip0jZD3x2ExuGDa3hcJHkVFeCELweYfF/HwSHf5iwpDkwFvsg5fBjYv19WLA/Wzg6RnWZ5+OaIA1ZOIqdUoJ5+1K2WAgw+1Pbt4/yUrJjHSCQCBy0TznqXPHiAqxkZIvu97aOPkEbh5s2fstFgomVE8rBciyrAATKnyjl65tT7L1WAA2dvby98JJT300+RX1SEM4cO4csNG7DpvfdwdPduVJWUiKy7EjgXwel7lofl4oA7qQKccecAnFPxHDxzat+1iAJ8Pz8SDsM3MIB+rxfVpaX48cgRbP7wQ3zyzjvYs307Ch8+hPf6dUx+8w1GGhowPT0tWy8OtgG+AWB5WC4O6PmaIEEBjlxZAQ7w+Qqag/wytU4o8Pz5c0xOTIjp5nxH5pkz+PKzz7Bx3Tp8u2MHrl68iBadDl20RPpptCOkUAJIUWRlAZs2yYqlwWm3opwUqCUD5rtN63IUqGs241rmJZyjEf25sBCG+npYTOQZ+nyy+2WC2iM9HWhOfq/FCQitVguNRkO/NaOwIB/nf7qOjPxSZOQVQ222iXuUpAqYvAFUtPeg2tovLnB7PSvb/hTBS+fePYAMNBn4tomzJ3l5eXA6nfDRYPV4PLh56zaOZuTCTPKplWyAFeBLIU6A8MVQRWcfymkJNek0sNFxvmpUXQVbZgZsep3ydyJettevXsG9u3fQbmrDrbx8nLtVJGTihApfNCnPAO1CTZ5hkSCpaCcl+AqNGv2/qZyWcJ0rgEv3i7Fz7yFcLihBLRkxy9XGM2CMU4ALHBPnPK5BH7msLtqq2noDNF3BX5XaabQ7aFfkJ8vjpjPAOxxBRkFlbEw8m5W4eKcYu05T9H/mmsgAvHREcrF8WWTQMVmJ2fxKNC8Ums+/vJRE8sXkhQL4H4ahpaL1zV9VAAAAAElFTkSuQmCC[/img]Trazar la rectas perpendiculares al eje de simetría, que pasen por cada uno de los vértices del polígono.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAAwCAYAAAEk8BksAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAAu/SURBVFhHzVlZbJNXFnb70Pe+VfNW9aEPnRmpqqZSl+nbqCOkggamLC1LGQYkylIBhYIYCFDKGtQmQCgCWiAp2XeCE5OwZLOzJ2QjdrwvSYjjxHHixIntb865/m3HsZ0FaOGTjvwvvv/5z73nnHvO98tco058dLgwSu63qCFzOIbhdo9jNvbdqgvcHB9zYd26ddJlYGpqKnzTTTcZOplM/DL2/ibd/NeypdKlML4N3nS7nPD7vEI06h5kZWYEbn6cEP2mLDKTyys9JAzLmBcy9Uj0jV4n3Siz+qRT4EJKivgtt/kgKzRMYWRkRFwYHR0Vv7dNU5ClqydCbxWUH1KuB17ZOubDkynMK33jPnyXLtmpH/UiMfEshoaGhJp4MJJ1oWntHvaKeQ9i06ZN0hGgVquxY8cOcdxDlocGyc3e0HocOXIEjx49Qmp2Nq5cuSKuBaGweMNrlKvzhAbNxtGjR8Wv2WzG5RotaaoPDCrQuZH6eHweceNG9zh2pZGmi0WqmGsaSz45Qmud32hEn9sfc3pny8CEH7LcBgM0/cPifeeC2cgPJhfgAbqhcezbt0+6FRsmowEWWlBZTr0BHbaAhtraWni90V7HaKhTQe+SBjyyRr5Sb2+vdAQcP34cLpeLXsmA3lEakFlngEIb8MogVn32GQ5RcLndbukKYDUZ8KCfjOYBZZqABv5D0JbLs1acB9xjv8+gARVmN9LS0qRbYaxfv146Amw0oNQyTQNUehQ+tkuXI8GJgGG329GgrMFvzRYKIBqQ2zEYFURBuXb1Kv0GwjJfTxGXptThZkz/iZTLjf24Z/VANjw8jMNZDeIJ/JznJbya/Lv6J0XAy/No/Tjk9YOjUClr0djQ8ExSVfkQNvJp9tdQ0LIbGihFqMl3nzwZIP3PBnZXTpRWctkIJZwQu/oo744Hcj2nlMzMTHG8WJhNRujopY00OyEl7O6ciTlGZuYuhsPhwPLly0MuMxcOHDiAgwcPolxRBi2FBcdSSEk2KWkb8qLJHK1kJjZ89RX2bt+OpKQkdHd3Y/PmzUhOTpbuhsGx1+7wontkhhIOq1JKkore8AY3GxcvXsTf3nsPSRSbH5HoKa/EA4ffXasX9/t84cTLoVhinIa8h/YFvw89PT04ceIEtm3bhunpaWloJL7//vvQdjUbrKTUPI1yUhRWQtGYp/egiELY74390Fi4cOECOjo6pLMwOC8UGT24Y54KK+GQz+qdRH6Xnbwr/prEAq/L5OSkOLbZbCIxNVCslBQXI+VuC/alN4SV8OacqxlDfosReYuQgjYzSrr6xTGPzW0xYevOXUhtG6Qc5AmUHU4qB9b8eAfVvYNQ6oaem6j0Q5B32PBV0h3I3GOj+MexvJj73rPIhyT/Pl0In2ccsvXJZehzTkYluGcVRotxCGfyaLrWnS8XF7jWibUpP40MeMgJ6Hl+eu6JXKo1WAmf9JODVFZVxcyqi5W6plaRhTndB5RcKBfm2SYApUpFR88OZWOzKBo44kJK+MRCu3iNUin+9KyobWiGiTIwzVxYCZ/QBo97Dx5g69atT53ig2AlnOZpacJK+MRA20hwumpqarBixQr09/eL88WihpToKM1HKKHlgG6M3mDGmnCRs53SekVFhXRlYRgYGEBtY6sos2j3nVtJEDx1J0+elM7io7q6Ghs3bsStW7dQ1/IoWglvuBrKi7GUMORyORISEqSzSHDxvnv3bvHwIKrrm9Hj9IHK2LASJ2nsdMZXwuiklL5z1y7894sv0Em7Ij+U180YY/OqrGtG+7AP1GAFlKwnJSZaoQpa4xplfCVaiwUJtCM6SP7y5puw0Hk8lCubqSGjMp+eG1ZC0V7eR2bGUWK1WvElFavvk4JrJMuWLZPuxMZdUqKgTnCAnhtSYqQThS1aCa8Fl9GnT58W52oq2H9JT8eePXvEeTywkjKLT6SqkBI9uVepldekHh6PR7jtqlWroFAopGGRMBgM2EXrEw8KUsJdXh8pORlUoqVov23xo0ReJmosvV4v/T0+Ll++DJ1OJ51Foqy2CcWmaVhnKuklHy4y+1CtqpP+Nj/GqdLcsmWLdBaJUlJSaJyClWYopIS2dhSaSMkc3hULx44dC1nto96C+1V2kl9zinFFqYdxdCqspIcCMc/gXbQSxpkzZ6SjQInElUprSzP2Hz8DI6X7kJJuqtGyddOorlFGdD8Lkb3f7gkdu6jYq3z4EB2dXbhSqxOZPUJJjnYSRe22qJJnPintGQwdF7SacepaBg4nXUOOzkPpXlLCacVMC8RtfKyWbDHCLd4v7cO41mpHWo8bfZQhRZycL1DiTEk71UmOmPXT0wo/b3eaEnJVV6C4Sy6oxdokOZJK29FksKPDMox2s+OlFPFuFgcedPfhwC0VNibfQYmyM1AKrz1fIZothp2mkUuw/pdU+N0GaJ8alXoPLrV/yKFlZ0O4vOMmm0s8brS5LLNQrKqtg+gyWElsL16MNugGRkRdyj01N+9cOnKzKPw3liG8CWhpUC1Vek7niKCKXrQYdFooG5qEIUEWItoQingmC7geZhaBa2Jm1bjQi0USvwiYaJMU9TVVJlxjM5vH3hXTEC6HmYHlxKl3jENBO/Ch/x1EYmJizKrnjwRTNaK8ponmEpuN4Qo4riFMuZjIkG6bA3X1zID5odFocOjQIaxduxanTp1CFbVJvNx/JIKGGMgQAxlinssQvsFcFPcPzEexa81mcphR5MJ36dKlgvNgyvuPMIp5LdGL0ERzPxJsfKIM4fTLrQPzXdw+MOfFhfdclBRTv0xHccH9888/h2iP5wV+/rlz5/D555/jaMJhNHU8JiP8oh1hDo1bkpiGkEfh8bAXvfTu7db5DZmJrKwsoZDLZSZmFwuuirkL4abum2++EZz49evX0dnZKe4PD9mp3WkSE62mlocJQW574hrCX0S0C1yRWOCSbu2XX4qY6qUKWU/dSxfN7JhEmzKYxayvr0dGRoag7NasWSO+yKhIXzww0VhDfZuGXF9DRrB7Tcw2hKs6Jh8t5HR3qWO5T61WuXZEtFvxiMi54HS5RFL46+uvY9Orr2LbK6/gz6+9hvc/+ADrN2zAypUrcePGDQwODi6ImmUwz8htG39PuEetW2V/oH1jOjDKEG7lmEnldo7ZVC66n8aQdlqBT959F8nU7nlJQHKR5MN33kHB7dvSvxYHwcqSIczMisnuC7SIz9WQpqYmERvs3/v378ellBRkZmeL/vXTt9/Gp2+9hT+98Qb+Q32SMw6zOx9mGsJ9blxDmHLmlpRpZ25L5WpHTEO4lyorK8OlS5fw9ddfY/Xq1SJj8ceq+cDuxG7V1tYGv58LooWDDeEWl2lsbnOZyuZWlw0RDUk8Q0o1tCK1KvRq1MjLyxNdJwfl2bNn0dzcLGgjbgwXi8rKStFS8+9ixi/KEO7f+Xs09/ByCvaKB5Uok99Ba2vrgmZ8oeCUumTJEuTm5oq0uxAw3898AH8bZ06AvwkyL8BlfKQhKr1o3/lzMrfw/M2QXWtinC7+DmDygo3JplhaCAb7rCivb0OJ1Y/b7DH0y8Vt9IqQIWp65xytBwVGHwq6A4Y8TdZaCDhGurq6xNdX3kxngkseXrXU1FRhaHk5JaP0W0i5+isSb+Zjf9IvOFdQBa3Dje8yGiMN4Q8mzHXwlxnmO/jrDBsyOfH7lvFXr14VBBpvkDPBhjJPXFxcDJPJJK45R4ZRLFfgxI0iZHTYYSWvjHItNoSpDv76w5xKftcQHlZWoalOhebGxt9NGsmAgvw8lNwujrjeQimdSZ/fUm/i5o3ruFeuQHp+MU5l3UP6YxcKDNOCQomOEQr2Didw87Eb2Ro3rcwEMsmgFy15FA8/Klqx8+wVnMi+LzigLO2keD82ZC+VKMIQLvA2nC/Dgcx6qO0TovKtGfCh9okXypdEVIM+1NlBv+RuA1402rkfoWOtHSt/uovE/DrIXKNOuF2jOJtThY8PZuGjhCL8PaHwpZaPJfnnsWyU1nfD73Hj/5uTiTfJaDJnAAAAAElFTkSuQmCC[/img]Realizar las intersecciones entre el eje de simetría y las perpendiculares a ella.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAuCAYAAAEgvhuhAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAAtaSURBVFhHzVlpbFzVGR0JCfoHISF+FKFUFWURNCDUHy1EbWlpKUsoIhWiYg+QhR3EmkIDSolCSAgtJGQjEJQEBRLXEK+JHdvjsT127NiO7XghXmZsjz3e581qexz79Dv3vZl5M/MmhoAKR/p8/e6978x5993l+75n0zQNoWAgzWyDw6PQNB+0QADaunXq/6HQjN6QBLsdLi1q0dDQAIcnktLw6KOqKOoxfiO3Y0JZ3ikf8k9pyPlag81KEZXaqECpoiIqk/89Q6OwuUUBqqoUdwyqweGZBJqbjSodqqHIFdCvDEWEajjU4YsrYrmvsh0DbPCOjGHyNBCamTujTc5Cv4HP5wnO6NzBoF6aEQ6rgn3UT/OGLp88iQkLFvwVF110E959912s27pV1bFP/IbS3pCqRE+PXprhdqui1B1K3JDfqanKGBYsWIILLvgDli1bBpvtRtTV1eDVtRv0ZwjKKD+86ctvZAHpq26wen+pFgz45e209VkOYaqVtbhh6x31o9JZrU8AmssF7Y7F0Hp743WV1TXoGZaZ4pbOzppj+hOuWKGXMTz2mCqcNbXoZmfXiB9V7Gw1hIT8Etu7hqRzj3SurJbOd91ltEKGDdi8ebN6ScE770SldO5k5w6vBrtTOtfVGV1TcPy4am8d8MHWPqihrKpGb3j7bb2MYe1aVZRVHcNJj3RuM3cmCguBNWtkaRUZFfLapb2FnVsHfSitNHUWUPMKGZnHH38c55/fjqYTJ9DMzidFS97X+uSPWUGXP+n/VRu3oql/AraXtx+ynAuptmpnDmycIG/sLrTscLa25tNCfeJxaveN+eENRTEcjspulcHCMxiKnNZLq3Yx3k8e14iWWDecUl5ZqvFpFcOsLPj77pPhLgV8Pr2OJa9NkyQGTjvycOolkfcFovo0jOGhh4x/5sHDDxv/yB4o9/cKTxI55zf36Dj5s8/qqk3IytqPq666AdnZXxg1Jjz3nCp4f4/wcB3EyTnPG4en4OA0J558Ui9N2LLlPZx77r3Ytu19o8aEZ55RhUPWFHk6ZK7GyTtkltv7I7CbZ7qhZl6Y+nHZ2PvDaJUJHifneiuR3TNpGREdHfqe0dJiVBhobNTrOzuNCh0kL5EdlusyTt4mj1HY7VdrMBPWvb1WluGvsWHjeqNGxxNPPCv1l2Pfvj34sqAIBxr7ZB1PJMi5RHPknCqtqEJINlIr+3jXTlx26QLs/mQXIqFg3Na8uVrqf4YP3v8P2tra8UXjoFrK8TOuqKkXFX1BlMgJ+V2tUngKG10YENEZnY3vYuRUrgGHZemmbMs94myMXN4ROkFC/sCGLMzMziFocTZ9WyPHjKw9cvIJbPw1LTpnuRHFLbZpzbNx0fzCRc4kcm9wGgOe/vhBqcwvYyd+iXbwIDQ5EzVxALSsLL2Obaa+nv4+a3Lf9BwGA9MI+P3G7DXwzjvApk1Ad7dRIeD/4rrJOWlU6OAPeINRaMKVRD4uFf2p5Nwv2tuNCwu0tQHPP29c6OQeIZ9IJR+dmkWvfypBXlmp23wQjzfma/qFvE8EjglXEvlwZBYun4nctEfPi6VLVUFytzaNEfEok8iHhLzHTJ6Xp5cm3Hzzn3DLLX82rkzIz1cFyV1CTqFJ5IPhWXRNmMiPHNFLAwcP7pHNqU7sGJYvv1/5PDH77MEHVR+Sd/um4U0l79RmcGIokiA3eStEKBTCwoW34ZprbsPMjOE6x1BWpgqSnxieRJd/Jpm8cTSKCtnk6VoqPP20Xn4TGH0DQl4hUcuJsWgyef3INMr7QglyjiMPivnQ2qr7ZoKA7CXlIrBxdDqZ/PjQFMrcwQQ5wbGUGzKCLoYxU4iArNgyOc3qh1PI64S8NJWcoBfw2WfGhQm7d6edsSRnoHE8lbxmMILiHv3EScP0NPDCC8CqVcCrrwIvvgh5q0ZjAiQvlsPimHcymbxqIIzD3XJoWJELgjJbzj3vFzjvJ5fi9KyEZgYC0t9m+ykuvnghBmXT+6KhF2Vdo8nkFZ4QCjp9Gcmzs/cJSZWyxYv/qMIj2k03XSd1wFNPbUJ9fT0K8vOQe6JHDoyvEuTlMlb0lUe9A/ED2Wxh6Xjdtb/Er65biEg4FD+cB2SbveKyn2PR9b9Rw/LWlo/VlE5SXia+RqqDnmoFnX5lVvVF7kmseHm1eBATsIvQOPkDG7Nku43KC7U+zb+NcVJ4hOtB4VTkA95hdebx174PI9fg0IgsETmg+Yfze2RsXDkyHmn4sRl9oFHRR51xt2VsfEJio1w8szUPdoly3cPiqivTfgTmh1tCh9ImN57+MBf/+ChXDbB6nfS3+Br6xgIIy9JjyEQbUTbzA5qugyanj4p9qJO+c5JwphN0t0t3p+qbWlDlrFbh2RntmFhtHZx1x/Uyk8Xa2d+Kx2T83frmk4aWGeVlMY1hKZyhIr0uxpD0vBiPhmUnnBf0vug8LVkCvPUW8OmnQEmJnps4elTf95lBYMxKB8rlMm7MjKAI4wPQe6MeenAMPTMKp0c3wHyXITzuCKSCuTGeHUzPUaRV/swKPDEPHwYeeQR45RUgEjEakkGvkMIHRDj10DucVzgTdXRHMwqnb8vw1+zzng1OnQJWrtR96BTEhNOlpZ55hdN77PVHxZOcUgF8mnCO8PsSl09OGhXfERxxOv7LlxsVOui2qeyEfxpu0UP3O6Nwrlp6ucxa0NNNE75jB7Bxo2w7w0ZFZvT19YoPmw+PeALzYmgI2LAB+OgjoyIhnN4ysx/0mJkBsRTO7KBXPOhuXxTd4kUzU5gk/O679cTQGdDZ2YEbb1wsXsa9YnvF/o5Fi/4isUm5PIRH1qUrzboHBzH8+edJ6WwKZyayRzxx6uGAMluTUbiKK4wRTxNOV7O83LiwhsNRgiuv/L0I/peYR+xNuf6tbCw7JWiyy3OXplmxcNauX4/wPfcYLAnh8RGXKZxReLtXQ8NIVBzrSTj6wiqdmuTqchHt2ZNxJ4hhejoqG00htm9/RyKNI4hGkxPxaeAOxS2U09AAowf+vqM/InoiKiJhrsZSOHNbjCqY32JkwRxXknC6yvffz9ScUfE9Yf9+PbgwueKMTJjGYnTCPBkjFObKMguXQKCMoy3+Y5pwYm4OeOkl4I03EknRs8X4OPDaa3ockYKYcLtooZ4GGdCMwpnwY6jFSIbhFhN/acJjKC7WtzA+QGoicD40NQGrV+v3yxy3ggrXRDhDNn6e4YCezCScyX5GR8Ui+qg41xTOMOKM4OvlNsavHa+/Duzdy+AdyMkBCgqAQ4f0a64NvilONboApxOBlBVUKCi/f1S0FLuCqJUB5UeGDMJl75QojplQRnK8cV7hFhifmoK91oHDjkMor6uQU09CyzNgdHRYvIBssSxxb6plNs5hKhJGeXUdimWaFPWGcUwJn8gsvFKE82NHYdfZCS8tLcLVV/9OtsEPxfjF5QNcccUN2LVrK5xOJ6qqquJWXV2N9ev/KX0uF3PgnHOcuOSSv4kvdgfycnOwdecu/HvPf7F68258Xt6A5v5xLH3vq3Th/NRT0S8B4ikN+af0zz6TEmF+G3R0tOLWW+8SIU+KlYutxO23LxG3RvwSC1RUFOHCCxkWbxPbj2uvXSYP5VBtU+JWZOfm470DR1ApIXeLsR0ySksSzn2SYTPz2oxuj9Y0orTCiZLK6m9sfNgy2X/tzhqxalXymvWZ+tudtaqfQw6cw6UO7Ny9V86A7djxyR7sPFyrvkhXyJRhjtxSOL/d8cmy2yfExpEtYfX/276St32gZQjbihuwq7wVX7Je9HDtpQlnzPnK9hw8sSUPxU29atvhQmiWjj+YiYbmfl0H9RxpdGPl5lys2pGTiDljUT4fgF8q+AZ+bEZd1EedepSv4X+lWkiEvEgq7wAAAABJRU5ErkJggg==[/img]Con el compás tomando uno de los vértice del polígono y la intersección entre el eje de simetría y la perpendicular a ella que pase por dicho vértice, que serán los extremo de un radio y luego el centro que es el mismo punto de intersección. Realizar el mismo procedimiento con los demás vértices.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADIAAAAwCAYAAAEk8BksAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAAu/SURBVFhHzVlZbJNXFnb70Pe+VfNW9aEPnRmpqqZSl+nbqCOkggamLC1LGQYkylIBhYIYCFDKGtQmQCgCWiAp2XeCE5OwZLOzJ2QjdrwvSYjjxHHixIntb865/m3HsZ0FaOGTjvwvvv/5z73nnHvO98tco058dLgwSu63qCFzOIbhdo9jNvbdqgvcHB9zYd26ddJlYGpqKnzTTTcZOplM/DL2/ibd/NeypdKlML4N3nS7nPD7vEI06h5kZWYEbn6cEP2mLDKTyys9JAzLmBcy9Uj0jV4n3Siz+qRT4EJKivgtt/kgKzRMYWRkRFwYHR0Vv7dNU5ClqydCbxWUH1KuB17ZOubDkynMK33jPnyXLtmpH/UiMfEshoaGhJp4MJJ1oWntHvaKeQ9i06ZN0hGgVquxY8cOcdxDlocGyc3e0HocOXIEjx49Qmp2Nq5cuSKuBaGweMNrlKvzhAbNxtGjR8Wv2WzG5RotaaoPDCrQuZH6eHweceNG9zh2pZGmi0WqmGsaSz45Qmud32hEn9sfc3pny8CEH7LcBgM0/cPifeeC2cgPJhfgAbqhcezbt0+6FRsmowEWWlBZTr0BHbaAhtraWni90V7HaKhTQe+SBjyyRr5Sb2+vdAQcP34cLpeLXsmA3lEakFlngEIb8MogVn32GQ5RcLndbukKYDUZ8KCfjOYBZZqABv5D0JbLs1acB9xjv8+gARVmN9LS0qRbYaxfv146Amw0oNQyTQNUehQ+tkuXI8GJgGG329GgrMFvzRYKIBqQ2zEYFURBuXb1Kv0GwjJfTxGXptThZkz/iZTLjf24Z/VANjw8jMNZDeIJ/JznJbya/Lv6J0XAy/No/Tjk9YOjUClr0djQ8ExSVfkQNvJp9tdQ0LIbGihFqMl3nzwZIP3PBnZXTpRWctkIJZwQu/oo744Hcj2nlMzMTHG8WJhNRujopY00OyEl7O6ciTlGZuYuhsPhwPLly0MuMxcOHDiAgwcPolxRBi2FBcdSSEk2KWkb8qLJHK1kJjZ89RX2bt+OpKQkdHd3Y/PmzUhOTpbuhsGx1+7wontkhhIOq1JKkore8AY3GxcvXsTf3nsPSRSbH5HoKa/EA4ffXasX9/t84cTLoVhinIa8h/YFvw89PT04ceIEtm3bhunpaWloJL7//vvQdjUbrKTUPI1yUhRWQtGYp/egiELY74390Fi4cOECOjo6pLMwOC8UGT24Y54KK+GQz+qdRH6Xnbwr/prEAq/L5OSkOLbZbCIxNVCslBQXI+VuC/alN4SV8OacqxlDfosReYuQgjYzSrr6xTGPzW0xYevOXUhtG6Qc5AmUHU4qB9b8eAfVvYNQ6oaem6j0Q5B32PBV0h3I3GOj+MexvJj73rPIhyT/Pl0In2ccsvXJZehzTkYluGcVRotxCGfyaLrWnS8XF7jWibUpP40MeMgJ6Hl+eu6JXKo1WAmf9JODVFZVxcyqi5W6plaRhTndB5RcKBfm2SYApUpFR88OZWOzKBo44kJK+MRCu3iNUin+9KyobWiGiTIwzVxYCZ/QBo97Dx5g69atT53ig2AlnOZpacJK+MRA20hwumpqarBixQr09/eL88WihpToKM1HKKHlgG6M3mDGmnCRs53SekVFhXRlYRgYGEBtY6sos2j3nVtJEDx1J0+elM7io7q6Ghs3bsStW7dQ1/IoWglvuBrKi7GUMORyORISEqSzSHDxvnv3bvHwIKrrm9Hj9IHK2LASJ2nsdMZXwuiklL5z1y7894sv0Em7Ij+U180YY/OqrGtG+7AP1GAFlKwnJSZaoQpa4xplfCVaiwUJtCM6SP7y5puw0Hk8lCubqSGjMp+eG1ZC0V7eR2bGUWK1WvElFavvk4JrJMuWLZPuxMZdUqKgTnCAnhtSYqQThS1aCa8Fl9GnT58W52oq2H9JT8eePXvEeTywkjKLT6SqkBI9uVepldekHh6PR7jtqlWroFAopGGRMBgM2EXrEw8KUsJdXh8pORlUoqVov23xo0ReJmosvV4v/T0+Ll++DJ1OJ51Foqy2CcWmaVhnKuklHy4y+1CtqpP+Nj/GqdLcsmWLdBaJUlJSaJyClWYopIS2dhSaSMkc3hULx44dC1nto96C+1V2kl9zinFFqYdxdCqspIcCMc/gXbQSxpkzZ6SjQInElUprSzP2Hz8DI6X7kJJuqtGyddOorlFGdD8Lkb3f7gkdu6jYq3z4EB2dXbhSqxOZPUJJjnYSRe22qJJnPintGQwdF7SacepaBg4nXUOOzkPpXlLCacVMC8RtfKyWbDHCLd4v7cO41mpHWo8bfZQhRZycL1DiTEk71UmOmPXT0wo/b3eaEnJVV6C4Sy6oxdokOZJK29FksKPDMox2s+OlFPFuFgcedPfhwC0VNibfQYmyM1AKrz1fIZothp2mkUuw/pdU+N0GaJ8alXoPLrV/yKFlZ0O4vOMmm0s8brS5LLNQrKqtg+gyWElsL16MNugGRkRdyj01N+9cOnKzKPw3liG8CWhpUC1Vek7niKCKXrQYdFooG5qEIUEWItoQingmC7geZhaBa2Jm1bjQi0USvwiYaJMU9TVVJlxjM5vH3hXTEC6HmYHlxKl3jENBO/Ch/x1EYmJizKrnjwRTNaK8ponmEpuN4Qo4riFMuZjIkG6bA3X1zID5odFocOjQIaxduxanTp1CFbVJvNx/JIKGGMgQAxlinssQvsFcFPcPzEexa81mcphR5MJ36dKlgvNgyvuPMIp5LdGL0ERzPxJsfKIM4fTLrQPzXdw+MOfFhfdclBRTv0xHccH9888/h2iP5wV+/rlz5/D555/jaMJhNHU8JiP8oh1hDo1bkpiGkEfh8bAXvfTu7db5DZmJrKwsoZDLZSZmFwuuirkL4abum2++EZz49evX0dnZKe4PD9mp3WkSE62mlocJQW574hrCX0S0C1yRWOCSbu2XX4qY6qUKWU/dSxfN7JhEmzKYxayvr0dGRoag7NasWSO+yKhIXzww0VhDfZuGXF9DRrB7Tcw2hKs6Jh8t5HR3qWO5T61WuXZEtFvxiMi54HS5RFL46+uvY9Orr2LbK6/gz6+9hvc/+ADrN2zAypUrcePGDQwODi6ImmUwz8htG39PuEetW2V/oH1jOjDKEG7lmEnldo7ZVC66n8aQdlqBT959F8nU7nlJQHKR5MN33kHB7dvSvxYHwcqSIczMisnuC7SIz9WQpqYmERvs3/v378ellBRkZmeL/vXTt9/Gp2+9hT+98Qb+Q32SMw6zOx9mGsJ9blxDmHLmlpRpZ25L5WpHTEO4lyorK8OlS5fw9ddfY/Xq1SJj8ceq+cDuxG7V1tYGv58LooWDDeEWl2lsbnOZyuZWlw0RDUk8Q0o1tCK1KvRq1MjLyxNdJwfl2bNn0dzcLGgjbgwXi8rKStFS8+9ixi/KEO7f+Xs09/ByCvaKB5Uok99Ba2vrgmZ8oeCUumTJEuTm5oq0uxAw3898AH8bZ06AvwkyL8BlfKQhKr1o3/lzMrfw/M2QXWtinC7+DmDygo3JplhaCAb7rCivb0OJ1Y/b7DH0y8Vt9IqQIWp65xytBwVGHwq6A4Y8TdZaCDhGurq6xNdX3kxngkseXrXU1FRhaHk5JaP0W0i5+isSb+Zjf9IvOFdQBa3Dje8yGiMN4Q8mzHXwlxnmO/jrDBsyOfH7lvFXr14VBBpvkDPBhjJPXFxcDJPJJK45R4ZRLFfgxI0iZHTYYSWvjHItNoSpDv76w5xKftcQHlZWoalOhebGxt9NGsmAgvw8lNwujrjeQimdSZ/fUm/i5o3ruFeuQHp+MU5l3UP6YxcKDNOCQomOEQr2Didw87Eb2Ro3rcwEMsmgFy15FA8/Klqx8+wVnMi+LzigLO2keD82ZC+VKMIQLvA2nC/Dgcx6qO0TovKtGfCh9okXypdEVIM+1NlBv+RuA1402rkfoWOtHSt/uovE/DrIXKNOuF2jOJtThY8PZuGjhCL8PaHwpZaPJfnnsWyU1nfD73Hj/5uTiTfJaDJnAAAAAElFTkSuQmCC[/img]Determinamos la intersección entre la circunferencia y  la recta perpendicular al eje de simetría que contiene al centro de la circunferencia. Esto lo realizamos para cada una de las circunferencias y la perpendicular al eje de simetría.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAyCAYAAAFtzWgaAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAAsiSURBVFhHzZl5UJXXFcCff3fajjPJTNvkn4xJJ/mjJradtKaGOqZq21QztWm1NmkbY5TUJZ00Oo6NU8AF1GhUFNy3uEAEtRAUEAIIiOw7jx1kE5FVUNlP7+9+73u8x3ssCm09M2e+9+537z3n3LPfz9Le3i7uUL9ISUmR1NRU/QSTkpKMF8C6997WT6CsrGzoRXt1sdwtyhBrxBfOLxi8vnWl/l1RUTH0YjhYOjo65ODBgy6oV7hD/cJk08Te3l6xNDc36z2TdqzRT+DBgwdiqa2t1X/gqrU8XyIiLklbW5tYiouLZXCgX1rKcvUEoKGhQSy5ubmyf7+/bciAW7duieXQoUMurB47dsyQY7ygSSBGa2urHmhraxGLJVj/Hg6ca3d3t7Hg7t27tmGRJmumligtYJNtxAAW3L9/31hQUlKiBwcHB6SlJEcvMPHNGS8pqq9qBd2+fdtYUFBQoBdYLIclcvta/Xs41NTUSF1dnbEgMzNT8vLyRsX9+/cPmcGjoGXv3r02omPDNl9fsWRnZ0t1dbW2CkeDHo5dXV3i4+NjLLBarXoHi2WpbNz4kf49HO7du2csyMrKksLCQj0YfflLqQw/po1oOMC/y4I0/w367FtKcyTv7G49ZgImqRdwpDk5OXowwed9J6VFrfudeHkbLKI0vSAjI0PS09P1YPbxbfbJzcVZUn3ltJIrWu7cadQ6sC9IS0vTC/LP75O7ypZu7l0nbVXGQZhQXl4umzdvNhbcvHlTvL3VasuvpL/7gW2KM9gXwA7nPDAwIHFxsbbXzhAeHi7BwcEGSyxwZzuOiL8WFRUZCxITE11ccSTs7Ow0XBQ9XLp0SS5evDhpGBERMeRwRA4IYS5QnQhio+zT399viAwB7BVLMW3WhOzsTAkNDbL9Gx9gDxDq6elxJkBgciTQ3Nyk1L5SYYIs+/0bttGxgViEBAQwOwH8gUBm+oQJFdFBUpPwb221t7MTJdxzjnTdrrG9dQ8Q4DQ4fycJmpqa7LHMhHjvZdJ+q8TJn1pKc6U88rxc27BYzRg0JjoABDgNJwJ4Q2lpqX46Qsrn/5DWigInAo7YXV8u8z3mqGPsUvhnlQhuaY+prKyUxsZGZwIYu+mjwGB/n+Sd2a191dywuThb7hSkivXiIQlbMVs6G6plQFlLQkK02rBBr0PJECHraNc0CeBJhEgTgoNOScwRP2lXEsRsXCLpgZv0hmMBBDgNUoKTBPn5+TpoAKtWfaRETlS4TIlrJKWxgE1DQ0Pl7NmzQuK9fv26bNmyxSBAvEDRHBFEQAIn4+b/8eC5c+ckLCxMR4WqqirjiMyqBK2j/YkiDLe0tKggfGfoiP6baMHjrl69qs/PXdB6XOSICRmWff7+WkGTDcdPnNAFhmXbtm16AF0QCR0j4+Mie5E18Qc7ATan3jVLA6wCv+Bpjo0HqbUgUF9fP0RgcHBQEyB9OUJIyDmprR09uA0HzB3lOhEgwSKaI4HXX5+pHC1KpkyZaRsZH5i5ZUwCM2f+WBFIVzhdRMWl8YKZW5wIkN44N0cCEPV8y0Myvr4qX62aK425ybY3owO5hT6AWGQn0NfXp89tuA4yA/8prWV5qjDOlZxT2yXrmGEQo4GZvMZH4IiPPVw3l2RLTbKS5sM3pKdr5GbBLQH6GxQznECWQ7FnYmtlkSTvXCMlYSdss5wBDyY7OhEg0OEYjgT6VI2Xc3K7CwGwpTRPCi8ESuqO1SpvnBYvr7WKScMQiMi0XHixnQDck+bICSY0FaZL6Ven3BIwMSsuTOcMi+WhLF++Sq/D2cjL1Pl2ApgVmciRgPXSEam7ec3txuTpWqWPK75r1ObzFF6T9es/1utu3LihvdmJAPGbP44EEn0/1Iod2jhT52TKlyur50thSKAqle/rXBwfH6XNGoAA+X1MAtfWv23vsiFUlxojYR94SGXMBenv7bbNcgW3BHAMQrZJoL6+QTYufEU6a8qkROkh8u8LpEJtPB5ITk7WBQQp004As4IqBLqUjVssLysMl4U//aFUxYbYlo4PiL7owIUAdSkEWlupSRcoLJTFi1fYlo0ORGMSfkxMjBw5ckR2797tTIAEjVhm6ZiamiI7d+6Qhw8f6v/jAeyfYgt/OnPmjCaAZWoCDMI9tQwiMhmPNBPOeJAS54RKk0jCXviVnQCUaULw5MdFNqWroUEjZNsJ7Nq1S9+DYKqO9c3jIBEBJLcEBQVpU9Vly/Hjx10auIliZGSkTsP2wouLIaIqoftJRnjE+Ey+LbRTWCh3Kn5+fhIYGPhEIyaz87PPtNGibq0BGCdEAUg3Gd3yZCM8YSXEDOIDjYF2AgTA0/AMgP/ULzxxjCcBOWmTJ0yIgovGQwc6dwJQAJgdp+mZjshmnEpXl4GcDuvczZ0oEoK4/8JhoTuqAKiHRUwmNRD73MHJkydl1qx5Mm3an+T55+fL0qVLlU0OtdeTCRQn8MaBwSv3KyMKQE1APGQyAiD9cKioKFGMP6Ny3WWFXFSCf5N3/rLANmNywRQALcMbYXlUAbA5MzK5EwAICDggL//gNfnmN96Uqd+eLa+98pLsWf4bKQ0NlI66CtusyQFTAMwH3ggybgWg3KYBoTZiMpdSIwkAcHGbdmCDKi0PS3tVkbSV56uy/oq+W6K0r4q/LD333H/seBRAAHiDT3gjEpkXLC4CkCjoGRgbSwDagszD3lJ7I2roi4DqUbgIaypIk9KIL5Qw7+nKszE7SQbV4TwOmALgm/BGgHErAGrCw6ntmEzpNZoASdtXq25thzp9q0PdPYRcH7aW5UtjTrKuv6PXLTLqdFWXPwogAJUZ9g9vowrwKBqI8/qrZB3d7HIV6R4zlaDF0pARLxkH/yVRnyyS9IBPpaN2bH8xBTA1MKIJcVeHlPQGlHqkakpAd4CjJvmtUs1fgLSpTtM90yOgMjO+MNQpf0ncukJ8Fv1EnvneDBXJfqHxxRd/psrOMBVtjGIbJun14AlhqJ2pEkcUgH6BFD2yAIO6B+dTR3l0kP4Y6JbREVCbVnmB9NaXS+Tpz2Xad7+vGPe1hWNwq2pFPBXDxtU5vFDm8IS3CQvAZ7z8IH/JPuEr9elxLp/0hiM231KWpxw7VerSYrTWYje9I1EfvyVFwfskLuyC/Hz2HHn66Wflqaeelblz5+mkSFIFHkkA4iwlBC8oI9wK0N+nQyV3By7mo8yj2Zqlkf/16V8rQf3k6tpfS7zP+zoytXD69zttu40NpgDwBG90RwhAMeciAHGWDIyt0Y+N5AMJny4R65f+0lFtOLC+Q1IRpzI2VNn1SuWkv5XMQ15SduWMPv2JAALQa8MTvJHEaCjdagAvJ/qgKhpFRwGs1kJ5990/ygsv/FK+861XZZ6Hh5zdvk7S9q6XxC0fSMqeT6T48lF50NxoWzE5gADcrnL68MbNEAK41QBxlvjPZEcB6uurZOHCP8iUKV4OznZUPGYtlqzcoU8YkwFUAVwD8EGGJxGIjwN07AkJCfZbDxcBcFoWUIEyiYWmADhUbGy0TJ8+QznaEpk6dZk899yPJDj4tH4/mYAfBgQE6M8mHCp8kaP4z+cTfpsCoB0nAfBwJsA4joMwZGeQOqmvr1dlQnqAe2qsR4+Z7ycLSaaU8+fPnxe+8lJgcvIHDhzQfskNxJgCkIFhngzI+P8aoUv9gyY8PT31LYTJE8yT1JwE8PX11SdOGY2joDo2+X8iAiAMvkhIhyeEMG8SiUJaAJiGebSwZ88eCQkJET498XyS0OSJz4ne3t4SFRWlhdEaAKnyaBZAup4nFeGPgo5o1d7eLv8Bw/D5Ea7mwFMAAAAASUVORK5CYII=[/img]Trazamos el polígono por los puntos de intersección que encontramos.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAwCAMAAAEuvIh4AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAKmUExURe/v7+3t7ezs7PDw8PLy8p2dnY2NjYSEhIODg4WFhYuLi7GxsfHx8YiIiL29vdbW1tfX19jY2LKysoaHh6ysrM7OzvX19f////7+/oeHh/z8/Pf39/Pz89XV1f39/fT09Pb29vv7++Tk5Nvb2+Pj49zc3Ojo6NTU1M/Pz8XFxba2tr+/v9nZ2cHBwd/f39DQ0GZmZvr6+t3d3VdXV5ubm9PT08bGxkhISLS0tFtbW+7u7pSUlFhYWPf5+X19fWtra8TFxWlra2RmZrK0tM3Nzefn56ywsD0uLkwICE8HBzosLJ+goPn6+lNTU46OjlliYkQAANAAANMAAHkAADc1Nevw8E9PT5qamurr60dSUmoAAP8AAKcAABUSEuXr6+vr66amplRUVLe3t3V8fDEAAJ4AAKQAAD8AAEpLS/Dy8pCQkFVVVcTExNDR0WNiYk8wMFcwMFBUVMHCwnR0dFxcXOfo6LS6urO6utvc3Orq6szMzHJycnNzc/n5+WdnZ8vLy7i4uFBQUKOjo9LS0uLi4uDg4MfHx97e3rm5uVFRUby8vNHR0eHh4aKiotra2lZWVsrKynZ2dnl5eWFhYYmJifHx7+bm4/7+/UxMTJGRkaenpFxcVVNTVWtrZdDQzK+vr8PDviIiMwAAYAAAfAAAO2NjbOXl4MDAwPLy735+egAAQAAA/QAA/wAAwCMjS8DAs35+fsnJye/v7H5+fQAAPQAA2gAAriIiRcHBtmRkZMjIyMLCvBwcJwAAYgAAlwICQFpaW9nZ16OjokVFQygoJ1paWMPDw2BgYPb29PT08Pj49qqqqubm5l9fX6GhoaCgoLu7u5WVlcLCwunp6Xh4eI+Pj5ycnLq6uqSkpIyMjHV1dZ+fn+Xl5a2tra6urqurq4aGhgAAANYH0bYAAADidFJOU////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////wBwHrofAAAACXBIWXMAABcRAAAXEQHKJvM/AAADKUlEQVQ4T41VsW7UQBB1mWYld/MD6OrTFCkmfRAVUUCxIIEGkEBWJDqkyVe4TRGhEChQUCpIkQjldEhIcbMln8Ob2bVvL7lA3tne2fG78ezMW7sSR0VTAiqiQHtSiU0Y99LAM9Z+YKrdCzY8SwNRV+kpdRguVDV0FSWqIVSk1BqJKE0w+gQ0JUZ8TLirxCMRtbFHVBFmmTAQ8nMdhU0pSQMXtrp9AWv3JWwL3mW/2TQ3Oy8Ca6Xa7JNzTJh48GPyRyvl2azGgqKiBBMWnjxgnkgVWPnmwX2PVbu1BKsU2dLsuQuoDH6SV8nVb/3CYwVFlFyKJtq1fojqJT4P2Y3B3I/H5imKmkZllFcU/stP3tgcDH7w9+E/vBz+9Bv1Svx6jOOQNkrjndlHFZRrxsUs5cDwN91aCHYa0tCFUPaoBFXxVtVwgF+oZQH0AvUEZQks6B1uKjpXQs0PPmmfPQmJbxLbWNQI5xAH5tRlQfTrUWNx8Nzkpx13y/PdFzl+9ufqT99DZEUcTFKlDUh84aeIyAmon1QuC0c/JIVClH7qsmUrTv4s8HkaUYrk/3h8kqhpi43x177/OHOPXNk11hbniOl6nvcieQlVof/iuYbN9RibxuLokp/Q20ljcUwOs5nqkQliHz3se88Ts9QwXOqa67pxv7WRv2CFPk4mE+wk6bGPbsI01FPVuI7uc4Q4vI/uBemz2lDN//7A4s7pVu0YIspxx085cklH2XQ+9nwFUJWRLqnKm+3d61hBx04fhDsgTh9/cMPpmpc69rBuyz0j7db29pOnpqbVdIiz9VdGwsHrN3uv5+9gQWEQ9nIyDjloFzOJMU0g1JXRAZ2GrOoFLHqiQys5xIhYZuRA9bEF76Dje1NkZPg3HfevljIyPS/T5XCn/V00qm+L980tunRfT0+/nZdJd4s211rjtZLotUe/uDz+ebKcMn9eyxnZrsp005v7rq99KHH2FhnhL/hqjfQU/Q5szGPTR2x5fNaM7mrO91ZBuqtG8ErL0XUf+o/+u8jnOh49HLhwDF0DkeVk7gH8KUUPZjnq9A0aUczsE619wAsFCrs3RP4CRGv7bZ3Vcz4AAAAASUVORK5CYII=[/img]Por ultimo con la herramienta de simetría axial comprobamos si coinciden el polígono simétrico con el obtuvimos. [br][br]