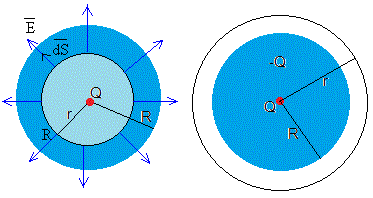
Aislador (dieléctrico): material donde las cargas están fijas y no se mueven.[br]Ley de Gauss integral: ∮ E · dA = Q_enc / ε₀[br]Ley de Gauss diferencial: ∇ · E = ρ / ε₀[br]La divergencia indica la densidad de carga local.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAnAAAAFqCAYAAACatmfDAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAADzeSURBVHhe7d3/ixzHnf/xV3/+gCizq590RojpMVy4BBluJR+6lcCCU8/ZvwSiY2d9JggCdmYOAge+XbySfzisJJ7BJHA/7EqBgAiXzCgIIgLa212DcmgmJic7QQsO90O2ByGEfpqV4uQPqM8PN9Wpqe2enf2qbe3zAYM1VTXVVdXVPW93V88GxhgjAAAA5Mb/8xMAAABwsBHAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5MxzCeCCIBh4tVotSVKtVvOL5latVtvQv/3UaDT2ZdvdbndgX3Y6Hb8IDjl3jpRKJT8bALAN+xrA2aBCkuI4ljFGxhjdu3dPQRCo2+36H8mt+fl5hWHoJydKpZKCIFCj0fCzMm2l7MOHDyVJjx498rN2VbFYVBzHfjJybitzbTPFYlHNZtNPBgDswL4FcK1WS7Ozs1I/eCsWi0ne/Pz8oTrBdzodlUolGWM0MzPjZ6fqdrvJ+I1ifn5+S/UDVqvV0t27d/1kAMABsm8B3JUrVyRJURQNBG9WpVJJTX8RHTt2TEtLS37yUMOu5gG7pdPpaHp62k8GABww+xLAdTqd5Dbb+fPn/ezE/Px88m97i9G+3Fs6bl6n00n+XS6XJW+NXdpn3PVp9jOWv6ZrlHV5bvnNbgO3Wi2FYZi67VarNVCXXb/m9sO2yS3rvi+VSsmt6sAbt6z6N8tL427jo48+8rMlr06/ry53u91ud2Bf2fH022b/7fbP33fBCGvy3H745f263DHx22jf2zLlcnnD5936h81vlz+/3c/Zbfn9Vsox4K9Dc/tt6+l0Ojp79qwkaXl5Oclz68raP/423XoBAHvA7INms2kkGUmmXq/72RvU6/WkbBzHyWfjODbGmIG0MAyNMSZ5b7sURdHA9tzP2DS7nWq1OlDG1tlutwfyfX75arWabN8YY8IwNJJMs9k0xuuX6bfZ1m3HyO1zGIYmjuOkHW7dxtmeradarSZt8fufVb+bZ9ti22nb7bPloygyxikvybTb7YG0tL763P7FcZy6z90y1Wo1dUxsn9vtdtJG28c0bj9tfbZPdmzdPHdbbhvtNm15f+ztPEgbm7S++tzxtWX8Ot1jzHjjZfnHoT9GcRwn27Lj4NeVtX82Gy9/WwCAndmXK3BbNTMzM/L6rZWVlYH3o6ylu3jxoiTpzJkzkqSFhQVJ0q1btyRJFy5ckPq3Om1+2pU1v/yJEyek/pWnND/60Y8kZ7thGCbbtreYz5w5o2KxKGOM1tbWRrqtHEWR5ufnNT8/r7W1NT9bGlK/JN24cUOSdO7cOUnS8ePHBz7js+UvXbokOePpGtbXnXKv1LqWlpZkjNHk5KSflcquKTx9+rQmJydljElubds1hJVKxfvURu12O/l8pVJJxtWOo33y8pNPPpG2OL9d7vIDO+d+9rOfeaU2F4Zh6rZHmWtZtjJeAICd25cA7vTp08m/t7I4utW/3Wg9efJkIH+nbICm/i0m++RmmrRt2/ILCwsKgiAJCLKe/LS3kc+ePasgCJL33W53R09yjvLFO6z+rKAv6zNZ5V3D+rrXarVaso4rqw+jtqPRaCS3FZXxOXceyQnY7Dyw42WDWWsn89v+z0Jae56nUcYLALBz+xLAFYtFVatVqb+2Juuk7q/puXHjRuYX8G7bLAjyv6TlfIlGUST7kyjDrqzYL+tmszlQvlgsJnn2Ks1u2079WQ9O+AFKmmF99aWN7XbY9VonTpzY9Eqs24779+8P5MlZe/bw4UO1220/e6ilpSVVq1XNzs4mwau9Sqddnt+2Hy+99JKftWtG2T87GS8AwNbtSwCn/i2WKIqklMDAfqHZK3X2wYHz589v6arEqOwXtr0FaoPLd999V3KuGthtV6vV1MDDXlFZXl5OFqe3Wq3MW6j2tpd7a9Iu7n/77bel/m09u/20hf/dbjdzwfsww+q/evWq5ARk9r823WcfRLFXU9MCoGF93UxafaOwV93OnDkzNLi07H53n7q0bbS3h8+dO6fHjx8n+aPodDrqdrsDgat7W3e783t5eTn5t71F/eabbzol/mIrgXqWVquV+hBI2v7ZyXgBALbBXxS319wFzvblL2x2F21HUZQs2LbNdd+HYZgsGnc/475vt9sDC6/dfHextklZnJ618N7y+2PLuw8YKGWxt9s2a1iebbP/4IF9uQ8cuOPn1jOs/mH1pXHr8sc7rYy/PV9Wfba/bj3+9uw+dNP9+rL4daXtJ/fftj3+HBxWp1uPGWF++9wHC9z6/H3kz2v33/689uty53lamj+e9t+278PGy9+2Wy8AYHsC838n7Bdet9tNrvz5PyQM7Cb35zh87q3UUTUaDc3OziqKoi3/fiAA4MW0b7dQgcPi0qVLG9b+2bVuo6wnAwBgM4fmClypVBpYML6dKyHAKFqtVupfM9jOlV//al4YhiM9BQwAeLEdmgAOAADgRcEtVAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AIdWp9NREAQKgkCrq6t+NgAcWIExxviJAHBYLC4u6q233tLTp0/9LAA4sLgCB+BQ+/zzz3X69Gk/GQAONAI4AIfa3bt3df78eT8ZAA40AjgAh9r9+/f11a9+VXLWxJ06dUrr6+t+UQA4MAjgABxaq6urevbsmV599VVJ0u9//3tNTU1paWlJ4+PjfnEAODAI4AAcWr/5zW8UhqG++OIL1Wo1SVKr1SJ4A3Dg8RQqgEOrUqno5s2byfter0fwBiAXuAIH4NBaWVlRvV5XHMeSpI8//tgvAgAHEgEcgEPJrn87c+aMisWiJiYmdPv2ba2urury5ct+cQA4ULiFCuBQun79ut57773kB3wXFxf1xhtvKIoi/fSnP+VWKoADjQAOAAAgZ7iFCgAAkDMEcAC2zf4h+LQXP4QLAHuHAA7Att25c0eSFMexjDEyxujOnTsqFAqsIQOAPUQAB2DbPv/8c01MTKhYLCZpf/VXf8Ufhx/R4uIiT7wC2BYCOADb9rvf/U7/9E//JPV/luPUqVM6efKklpaW/KID/Nutaa9Go+F/7IVx/fp1Xb9+XV/60pd05MgRLS4uJn8JIkuj0VCpVFIQBCqXy6rValpcXPSLATgkeAoVwLaNjY3p2bNnyftqtar5+fmBMkjXarV0+/ZtraysqFKp6IMPPsi87Xz58mUtLCzol7/8pSYnJ3X58mV973vf4y9HAIcYV+AAbIv9IVy7/q3ZbOrkyZN+sV3nX6nLwyvNo0ePFMexTp8+rRMnTvjZidXVVX3ve99LgjdJOnLkiCYmJgjegEOMAA7Attg/BG/Xv1UqFb3zzjt+sVR+gJP2yrqFah+WyNPLd/36dR05ckQ//OEPdf78eZ05c0bvv/++X0yStLy8rDAMk+BN/VvXFy5cGCgH4HDhFiqAbalUKhobGxu4ZdpoNHTkyJGRA7nDbnFxUb/+9a/13e9+189KlMtlSUrWFa6uruqVV17RnTt39Prrr3ulARwWXIEDsC0rKys6d+5c8r7T6ejDDz/U3/zN3wyUQ7bXX399aPAmScViUWtra1pfX1en09HPf/5zSdKrr77qFwVwiBDAAdiyy5cv69mzZ5qenk5ueZ49e1bPnj0buNV3mHS7XdVqNQVBoLGxsV17QtRezXz55Zf1ySef6Pjx46x/A8AtVADYDe7t48uXL+u3v/3tpj+nsh2VSkVhGG565Q7Ai40ADgB2WavV0qNHjzQzM+Nn7djY2Jj+8z//k/VvwCHHLVQA2EXr6+u6ffv2ngRvnU5Hz549009+8hP+1ixwyHEFDsChd+rUKS0tLe14Xdn6+rref//9oT/KCwC7gStwAHJpfX1dtVpNY2NjyYMDq6urfrGhyuWyut1uEmxVKpXUOtbX11UulxUEgRYXF5M/GxYEgTqdTlLGDd74G6cA9hIBHIDc6Xa7evnllyVJn332mYwxevr06Zb/EsT8/Lx+/OMfa21tTeVyWd/85jdT6/jBD36ger2uKIr0k5/8RD//+c+1tLSkQqGgr3zlK5Kk999/XwsLCzp69KiCINBvf/tbvxoA2DXcQgWQO7VaTU+fPlWr1fKztmR1dVWzs7NaW1vT1NSU/vEf/3Hoz6CUSiVNTEzseLsAsFMEcAByJ0j5+6Ltdnto8JWmXC5rfn5etVpNP/3pT/X+++/rnXfeSb0K1+12FYahHjx4kJoPAPuJAA5ArnQ6HZ09e1ZxHCd/h3WnRnmIodVqJVf+AOB5Yw0cgFyxa85u3bqVpPk/qbG4uKhSqaQgCJK/JTrMp59+OjR4k6R79+7xB+QBHBgEcAByZXx8XM1mUx9++KGCIFCpVNIPfvCDJL/T6eitt97SjRs31Ov19OUvf3ng89u1srKi1157zU8GgOeCW6gAXiiVSkVf//rXValU/CwAeGFwBQ7AC+WPf/yjvvSlL2l9fV2XL19Wt9v1iwBA7hHAAXihXLp0SW+99ZZefvllfe1rX9u1Bx0A4CDhFioAAEDOcAUOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgsKsuX76ssbExBUGgy5cv+9kAAGAXEMBh17RaLd28eVN/+MMf1Ov19Nvf/latVssvBgAAdmhfArhSqaQgCDJfe63b7SoIgm0HE51OJ2nr6uqqn42+L774QoVCQZI0Pj6uYrGoR48e+cUAAMAO7UsAt7a2pmazKUmK41jGGBljFMexJCkIAjUaDe9Tu6Pb7SoMQz95SyYnJ3Xnzh0VCgWdPHnSz94zq6urqlQqSfBYLpf3JYBsNBqZtz8XFxeTgLxUKg0ExRcvXtT4+LiOHj2qUqmkTz/9dOCzAABgd+xLAJelWCzKGKMwDDU7O6tOp+MX2bFisZgEijvx+eef6/Tp037ynllfX9drr72msbEx9Xo99Xo9FYtFfeMb3/CLJrrdrsrlstbX1/0sra+vq1wuq9vt+lmJ1dVVnTp1SrOzszpy5IifrU6nozfeeENXr16VMUZvv/22pqenk/02Pj6upaUlGWO0trYmSfrqV7/q1QIAAHbquQZw1o0bNyRJP/vZz/ysA+Pu3bs6f/68n7xnPv74Yz179kzz8/MaHx/X+Pi4PvjgA8VxrMXFRb+41A9Wi8XihiDOBm82P02329X3v/99LS0tKYoiP1vq75+JiQlVKhVJ0szMjAqFwob9tr6+rlqtJkl6/fXXB/IAAMDOHYgAbnJyUpK0srKSpLnrzvz1azav2+0O3M5zuZ+/devWQJ76C+7d+jdz//795GqSrfvUqVOpV7uU0v6sV9ZVx7S1Y+Pj41L/amCW+fl5nTp1KgnibPB26tQpzc/P+8UTxWJRrVYr2UaalZUVXbhwYSDt9OnTA1f1VldX9fLLL0uSlpaWnJIAAGC3HIgATtLAOrVOp6OzZ88ma+Wazaamp6fVarWSPPuZlZUVxXGsOI6TIM+WsevtHj58mNStfvB27969pP5qtbohAHStrq7q2bNnevXVVyVJv//97zU1NaWlpaXMgGdycjKpf9jLBq8+exXMXRs46kMYbhA3SvA2qjiOU2+tLi8vJ/8+efKknj59mlw5BAAAu+/ABHDuOrWrV6+qXq8n7yuViqrVqq5cuaLJyUm12+3kM2m3Be3nbfq77747kH/jxg0tLCwkV8EWFhYUx3Hm+rDf/OY3CsNQX3zxRXJrcLOrVTt18uRJNZtNffjhhwr6VxjtVblR1pXZ261xHOuDDz7ws3eVffIUAADsjwMRwNnbiPb2nF0A7zpx4sTIDyOkfd61tramdru94WqYHwhav/rVrxTHscIw1MLCgi5evOgX2WCnt1DVD1yfPn0q038owF6V++u//mu/6Ab/8i//ojAMFYah3n//fT97WwqFgr744gs/eV8f7gAAAAckgLt06ZLkXSm7e/euU+L/bOXnQPzbpq5SqaRPPvnET860srKier2eBJAff/yxX2SDnd5CTfP9739f1Wo1M9C0arWa4jjW0tKSlpaW9OmnnyZXDnfiwoULA+sU1Q+G//Zv/3YgDQAA7K3nGsDZH9iN41jNZjMJTK5evarl5eWB9V8/+tGPdPXqVefT2d5++20tLCwkV7fsQwx2Hd2lS5c2/GxJo9FIvYVq17+dOXNGxWJRExMTun37tlZXVzN/K2232d+DG+V2aK1W06effpqsz7M/7bGVIG59fT01AP7mN7+pzz77LFmLd/36dT19+lTf+ta3/KIAAGAvmX0QhqGRlPoKw9AvbowxptlsDpRrNpuZ6e77er1ujDGmWq0mafbftg5jjKnX66mf8127ds0UCoXk/Z07d4wkE0WR6fV6A2X3wtTUlAnD0NTr9U23F8dxZrt6vZ6JosjEcexnJaIoGthXExMTZm5ubqBMvV43hUIhyW+32wP5AABg7wXGGOMHdQAAADi4nustVAAAAGwdARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMDhuWq1WgqCQN1u18/KjSAI1Gg0/OREt9tVEARqtVp+VqZaraZSqeQnJzbLH6bRaCgIAj8ZAJAjgTHG+InAfmi1WpqenpYkxXGsYrHoF0GKWq2mhYUFhWGotbU1P3uoRqOh2dlZSRKHPgDkF1fgDolyuewnbVur1drS1aQslUpFzWbTT8693RqfLPPz86pWq37ySGZmZlSv1/1kAEDOEMAdAo1GY8tXaoaxV82QjvEBAOw1ArgtaDQaKpVKCoJgy2uaXPbzaWunyuVykuevcSqXy6rVasm6Mb8Ndm1TuVxWo9FQt9tVrVbT7Oys4jge2J7bj8Bbg2brrdVqA/l2LZf6QYr9t7x212q1JD2NbWcQBHr06JGfPbDdYVcO3fVzWeXdbbnj2el0FPTHw80rlUpqNBoDn+t2uwNj7u4zd31b1vjYbXU6neTfbt12u27d5XJ5Q1/sGPvzQl4//TbKG1MAwAvAYCQTExNmYmLCPHjwwM/aEkmm2WwaY4xpNptGkonj2BhjTBRFpl6vJ2XDMDRhGCZ5kowkU61WjTHGVKvVJD+OYxNFkTHGmHa7PVBvvV5PyqW9D8MwqdNuw22nm2/L2DzTb1u73R7Id/vhStu229ZqtTpQt79ty46dpKQ+22+77Xq9PtCOKIqStvpjaZy2uHXYNFuuXq8b9Q+bOI43jJXxxsfdljtGURQNfMaWtXmSkv1p02wb7Hbdfe/W77bR9MfUrcu2BwCQX5zFR9BsNk0YhqbX6/lZW1Kv1we+SF32i95lv5jtF737JW68YMgv6/KDJpf9Mt8sQMvKd4MY95XVTzfQMClBrF+PnEDFZz/rcoNaNyBzXyYlyLXCMBwI+vzgx99m2rj77+22/H67Y+rvNxtsmoy54fbTT3f7advn9tMP8AAA+cMt1BHcuHFDcRzr6NGjqbeoWq2WxsbGNDY2NvS26sOHD/2kxOPHj/2k5KnMtNuMvmKxqGq1mty682+/+Ww/jDGKosjPHtmTJ08UhqH6/zOQvJaWlvyim/5UiM3369rK+r0TJ04k/47jWHEcb6jvIKhUKlpYWEj6PGwfp80Nn71Feu7cuYEHQ548eTJQDgDwYiCAG8Hy8rKazeZAEDAzMyP1g45araY//OEP+tWvfqXp6Wmtr6/7VUj94GKzYKTT6fhJOn78uJ+Uan5+XsYY1et1LS8vZ65FK5fLqlaruxLMHDt2THEcbxqcubICEhuwpo3BqB4+fJisEQvDUPfv3/eLHBjValUfffSROp2Ozpw542dvkDXGrVZLCwsLMsaoUqn42RKBHAC8cAjgRjAxMaHbt28ngZkboH388cc6ffq0xsfHdfLkSU1MTOh///d/nU//xcWLFxXH8UBg1el01Gq1VKlUFIahzp49m+S1Wi2FYZj5pezqdrvJVbdhPxVhrxy6wcDy8rJTYnT2amMURbpw4cJAXlrwWCwWFUXRwFOaN27ckPrBVrfbVbVaHRgDZdTlsu3odrtaWFjQlStXJElvv/22pqenB/q6WV27yT7YkOXNN9/UwsKCfvazn2lyctLPTtj977Z9YWFBcRwPPNBgt3Xv3r0kbXJyUmEY6tKlS0naj370I6l/FRYAkFP+PVVs9ODBg2Q9VaFQMFNTU8l6OH9dm7+g3+evGfPXirnrttw1Tm66XZPm1hPH8UCa+1l3IX0cxwPv1V//Zj/jptu1c+52jbPIPusBALudLG5Zu223vK3fvrLG065Hc/vtryXzx6nZbCaf8+t30+zaN/vero1zy/z3f//3hrqNNz7+WPt98dfcGa//dsz9eeOvgUsbU2WsLbT5AID84i8x7ND169f1i1/8IlnzderUKf3whz8cekUFu6PV/0sOTGEAwGHDLdQd+ru/+zvdv39f3W5Xq6uriuNYX/nKV/xiAAAAu4YAbodOnjyparWqMAz12muvaX5+XuPj434x7LJGo5GspXN/EBcAgMOAW6gAAAA5wxU4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZAjgAAICcIYADAADIGQI4AACAnCGAAwAAyBkCOAAAgJwhgAMAAMgZArgcCoJAjUbDT0aKWq2mIAiSV6vVSl67Za/3R6PRUKlU8pMBAIcYAVzOBEHgJyFDEARaWVmRMSZ53bt3T9PT037Rbdvr/dFoNDQ7O+snAwAOOQK4nDHG+ElIUS6XFYah1tbWBtLn5+dVrVb16NGjgfTt2uv9MTMzo3q97icDAA45Aji8cDqdjpaXl/X222/7WZKkd999108CACBXCOB2YHV1VZVKRUEQaGxsTI1GQ+Vy2S82oFwuJ+uxarVakt7pdJL0TqezpTVaaeu8himVSqltaLVaA/W4ebVaTeVyOWm/XfPVaDQGPmNf3W5X6t9idF/DuGPg1qF+Pa1Wa6Cvbr7rk08+kSSdOXPGz5IkFYtFzczMJO/9fnc6Hcnrm1L2URqbb8fHjpc7L0qlkhqNxkD93W53oB1pa+o2ywcAHCIG2xLHsSkUCqZarZper2d6vZ6RZObm5vyiiSiKTLvdTt5LMvV63RhjTBiGA+nNZjN573M/1263jSQTx7ExxphqtTpQly8Mww2ftW1yt9tsNpN6q9WqkTRQ1i9j+tt2p1S1WjVRFCXv3Xb72u32QNl6vZ7UZbftti8MQ1OtVpPyLtsOt61Zms3mwHjZ7drP2j5acRxvqNvvlzvGxhuHMAyTvrj7XlLSH7fv7nubb9s0bI4AAF5sBHDbNDU1NRBwmP4X+Z07dwbSLPvF77/cL/asgMTnBwxWFEVGUmYA5wcrWWzAIC848/tbr9cH6vODScvte1q7jRN0+a+04NL0+5o1XlsJ4MIw3BAIRVGU9HW3A7hR8v1t+uNsvDYCAA4fbqFu082bN3Xp0qXk/erqqiTp1VdfdUr9xZMnTxSG4cATkcYYLS0tSZKuXr2qhYWFgVt2o7K36a5cuTJ0wftmC/ftLT1JarfbfvYGFy9eVBzHye3ETz75RGEYqlgsSpK63a6CINCFCxdkjFEYhl4Nf9HtdtVsNjeMz+TkpF90U+fOnZMkPX782M/aII5jP0nFYnHDww8HjR1jAMDhRAC3DTZgeemll5K073//+5qYmND4+LhT8i+OHTumOI4z121VKhUZY5LAadTf/Wo0GlpbWxsp2Dl+/HhqwKJ+n2ZnZxXH8cD6sGGKxaLq9brOnj2rIAg0OzurlZWVJP/ChQuq1+sjBUPFYlH37t3zk7elUqkoDENduXLFz0q4a9LStjvq+D8v3W5X58+f95MBAIcEAdw2HDt2TJL0+9//Xuvr67p8+bLUD1iyFItFRVG0oYx9UMAGDJOTkyNd/XK5Qdndu3cH8lyVSkXygpdutzuwIP7JkyeS8yDAMJ1ORw8fPhy4YuZfGXr48KHU305W8ChJb775phYWFgYewGi1WpkPC2xmZWVFcRxvuJpprwraK5/1en3DdhcWFjYEfzbw/uijjyRJZ8+eHdo2t98LCwtaXl7e9AGXYdzgv9VqaXl5eeRAGwDwAvLvqWI0c3NzRv01bA8ePDCFQiFz/ZvLXcQuZ72Yu+7MTfe5Zew6KjfNXUuWxS3vrq2ya+j8erLK27Va/stfP2Y/Z+vPWrvm11etVjesHbTrwfxtZfHH219LZlLG3l8759Zhy7pr89w8k9Jvd42bW96mu2X9tqTNj7Q+AAAOl8D835cKdmB1dVWvvPKKer1e5i3UF5G9AuXfum21Wjp9+vSGq3EAAGB3cAt1F/zmN78Zuv7tRXX27Fk/SZJ048YNgjcAAPYQAdwu+MUvfqE4jrW4uOhnvdDa7XbyAIP7suvLAADA3uAWKgAAQM5wBQ4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGcI4AAAAHKGAA4AACBnCOAAAAByhgAOAAAgZwjgAAAAcoYADgAAIGde6ACu2+0qCAK1Wi0/a1vK5bLK5XLyvtVqKQgCdbvdgXLP0273uVQqqVar+ck7UqvVVCqV/OSRdDodBUGgTqfjZwFbthfzyT9PvCh2ctxKUhAEajQafvIGjUZDQRD4yQfSVsakVqu9kPMCz88LG8B1u12FYegnb1u5XNby8vJAWqVSkTFGxWJxIP15KhaLMsaoUqn4WVtWKpUUx7GfvCO1Wk0LCwt+8kg6nY7Onj3rJwPbslfzaWlpSUtLS35yru3kuLWMMZqZmfGTBzQaDc3OzvrJB9JWxmQrZYFRvbABXLFY3NXgY2lpSVEU+ckjq9VqB+pK3SjW1tZ2NQiWpPn5eVWrVT95JJOTk2q3234ycuAgXnlgPo1uJ8ftVszMzKher/vJO7JX596tjMlWyu6lvRqLg6jb7e763aOD5oUN4A6STqfD/33h0Gq1WhuuXgP7gXPvXxy2sXjRgzftVwC3vr6ucrmsIAi0uLio1dVVnTp1atO1J6VSSUEQbFg7YdeelUoltVqtoXX4bDvsa7PP2jakXUHw12rY9TS23larpVarldymCcMwqcd+Nq1/5XJZtVot6WeQsqbNHRt3oqat6XHLBiOs2Uur17Jr7Nx+WnZsG43Ghs/avKz1Iln7ehRb6Z+7j7Lan5ZXKpUG9pnN8z8TOH30t5U2hyx/XLPGyW2DUuacnONDzr4ctm13LadffqfbazQamp6eTvLceeHut2Hts2zZwJkjtg5bb61WU+CN37BjLY3bx3K5nBzH7vHY7XYHxss9Pksp60az5rc91m1+q9UaeS5YbrsC53xk6+l0OgPzdBh/zg47lnx+O9wxSFub6/bZHy/XsPGw7e12u0l9Nj/r3CtvLvnn1s3s9Fzmzkd/2+5+GjYmcuZ64B0//jFq527aWAw7Nmr9NXu2TWl9kVfHqPsmTVp52053XPw5mTbepVJJy8vLWlhYSMbB1m/b67bFrcM/F9lxrtVqm+6TfWf2wdzcnHnw4IGJoshMTU2Zubk50+v1TKFQML1ezy9ujDEmDEMTx7Exxpg4jo0k02w2kzw3vd1uD3zW8j/XbDaN2+UoikwURc4nBoVhaOr1ujHGmHa7bSQl5ev1upE0UJ9tlzFmYLv2s35/bLttXabfJltvtVo1xhhTrVYH6k5rV7vdTv7t1+1/1tabJm28bPk4jgfqsvlxHJtms5m0yd9mFEUDdUja0CZ/bGwbfG5/Tcq2hvXP3w/uuA6bG2EYJuPqStsv7nzK2k9p0sYoawz8trrzyea57R22bbe87Ystb9u+0+35nzf9sXH7J+fYSqOUeWn3ozt2xpsTw441k9JWf47Ybdlt+/nGa5udK257sua3e6y79W11LrjbsnPSfs6+bP/k7Fdfu90e2Af+WPnz3ee2091Hbltsfr1eT/5drVaHbjdrPOy+cMfQH6+s/WX5+38zaW3xzwFp+9r0+yln/G0/7bajKBpoh1vWV61WB+aEe95z2zNsLGz70o4N29bNxqZerw+00Z43R9k3rrTybpptg9tP+97vj63f3VduXe7nbR1um+Sci9rtdlLezumDZF9bE4ahmZqa8pM38HemP/AaMrFd/g512RNt1pdGs9nccLKyk9PyTzT+5LL8A8flHijWsC+ktHa5hp2Q/HH01ev1DePh9sn21381m82BE7bLtsdVdb4INtvXvp30L4qikeZN2twInWDMGrafXHZsstrtcscjbd6alBOJfyLeLN/nlzebBLd+fVvNT5vDw/Zr2rx0jbof0o41f7v+HPHPIba8O8/dfOMdM5vNb7/trlHmQuQEge7L/cJ0xzRtHlvu+Lgv+3l3Tgzjnieyvlz9c6crKy9tPDbbH36+eyy6r6wxcdm6XFs5l1W9QNU4c8WOj//yy1t+OTmBpDv/XP5YuNKOjbT2+uy50n+ZjO1pyFwepbx7vGw23v6xlVb/Zuci998H0b7cQlX/Mngcx3rvvff8rA0eP36sKIrUDzCT1/z8vCSpXq9rdnZ2w2XQUdhLpSsrK0MXlT569MhP2tTVq1eTS7bBJrcq7GXZc+fOqdls+tmZttMu2x5jzNAHMR4+fOgnDXj48KHq9fqG/VKpVFSpVBSGocIwHLiU/fjxY7+aAZvt61GM2r+1tTU/acCoc8O6dOnSwJqSu3fv6sKFC8l7e0vp3r17mz5QYy/vX716Vf933nq+Tpw44SftmrQ5fOzYMSljvmw2LzezlWNtszmyVduZ31uZC2tra2q32xvq386T8d1uV81mc0Ndk5OTftFU9taUpE0fDrFPo9pj17+V6NrKeGzm0aNHqlarG/q42dOxypibru3sa/v99eTJE4VhuOGzaU8z21uIflk7d/fje8iK41hxHG9oy37Yznj7NjsXTU5OKooinT17VsEIt7X3274FcPfv31ehUNDJkyf9rA1eeumloYueZ2ZmZIxRs9lUHMcb7llnsWtNzIgnuM2+dH32Z0XsySsruGy1WlpYWJDZxs99HD9+fEvtKpfLyQlrFMO+wE6cOKG7d+/6yYm1tTWZfhA1Ozs7cFL21y1Ym+3rzWylf6VSKTMY2OrcUH9/R1GUnCjX1taSk0e329X09LTa7fZIJ5SzZ8+q2WymnrCfh4cPH2bO390Qx3HqnHjppZf8JJ04cWLovBxmJ8fabtjO/N7KXCiVSvrkk0/85G0pFou6d++enzySTqej2dlZxXE8UjAkJwAJw1DT09PJmkrfVsZjM8ePH9fKyoqfvCVp81bb3Ndra2s6d+6cjh07lnlM+Oz5KWu89uN7yArDUPfv3/eT98V2xjtN1rjbc9HS0pKMMapWq1pYWMhcC/g87FsAd+/evYGrE8NMTk5uWHQq56kSOyErlcqW/6/B/SIYdiBfvHhRcrbZ7Xa1vLys5eXlDe2ybLuG/TyBu/PtpNnKSdMeaG4but3u0EnlTs5hE/7NN99UHMdJXZ1OR3Eca2FhQbVaTRcvXtTy8vLAttxFsjbd/ckV2173/1wWFhYUx7FKpdKm+3oUo/bPXjFzA8tGo5F8ftS5YTUaDV26dCn5IkoLMuz/tY9ykrP/N5h1YvbZdn/00UdS/4tu1M+msePS7Xa1sLCgK1euDOTvxvYajUbyBe+eD27duqUoilKv9ly8eFFxHA/MCTvvLHcO2EDC/eIa9Vi7cOGCZmdnk/JZwfyTJ08k53ienp5OvYq03fk96ly4dOmSZmdnB8q5c3or3nzzzQ3HR2uLD4nZcdksqGw0Gsl2Rvm5olHHY5hGo6FKpbJhLm12/rR241zmnp/sNiuViorFoqIo2vAdmTVPqtXqht8w9L8f9/J7yHr77bc1PT09MN+y2rzbRhlv9fuXdmzKuRKcdS7qdDpJfQflp2AG+PdU90oYhubatWt+8lD+vW3LX6uRxl9T0Gw2N6TZevx74JZ7jz3sL1C3awL89WBpaf69fNsO460d8PtjX/Yevr8dtz6lLD63L/cevn3Z+rLWNrhrRKIo2rCewq/P1tPsL6Z2t2Oljbs/5m6+Mvapv+2d9k/O2pe0Nqo/tn665e8bv05/POy/09aAuHPHjrtbl89tl/1su93eMAf9/qZt25YZ1sadbM8dW3ctiVsua39Z/v5xy/tzoJ7yYIvNc/t48+bNgc/ZtqWtK/PX4bjbcvP9bVl+fX5Ztz9bnQv+PqjX6xvGxN8vbttcWeXccfOPXcsdl2Hj3Ow/8OSWsX3z++KnuePhH5t+222dbr5JmUu2P256Fv+zWz2XuX1Om/N+n9LWq1n+PLXz1x/D7XwPuel+/3z+ebDprIl209z3/lz28/339pi2792xc8vJGW87DmH/IQW3jL+mzc3zzy1Z+ywMw03HZq8F5v8aD2CL3KtJo6QfVK1WS9PT0+JUsFG3/xddms3mtm8zIV9arZZOnz6defUVOCj27RYq8CKxa358O7nFA+D56fZ/b+7evXsEb8gFrsAB29RI+buNURTtymLr/eL3IY5jvrz67NU3i6twAA4SAjgAAICc4RYqAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMABAADkDAEcAABAzhDAAQAA5AwBHAAAQM4QwAEAAOQMARwAAEDOEMAhVy5fvqyxsTGNjY2pVCqp2+36RQAAeOERwCE3Go2GVlZW9Ic//EG//OUvJUnFYtEvBmAfdbtd1Wo1BUGgsbExLS4u+kUOvE6no3K5rCAI+B9D5AYBHHLjww8/1M2bNzU+Pq7Hjx9ramrKLwJgn926dUsnT56UMUbValX/8R//4Rc58K5evap6va5er6dSqaRbt275RYADZ18CuEajoSAIhr4ajUbyf0BBEKjT6fjVDFUqlRQEgZ+8K9x2Pg972bc8efbsmY4cOaJOp6Naraa///u/94tgiFarteXjCtjMzMyM3nnnHUnS1772NZ0/f94vMmBxcVFjY2N+8rbtRn1LS0s6efKkxsfHVSwWdebMGb8IcODsSwA3MzMjY0zyvlqtyhiTvMIwlPoH0XbFcSz1L+fvtna77SclOp1OEtxtZduNRsNPyrSXffP5gfVBMjU1paNHj+q//uu/FIahXn31Vb9ILq2vr6tWq2lsbExB/zZUrVbT+vq6XzTRaDSSwD4IAlUqFa2urib57ry0r+np6YE6XK1Wa+j+Xl1d1alTp1LbtLi4qFOnTiXbOXXq1MBttLS22Fer1UrKbdYnV6PR0OXLl/3kgf8JdF+lUskvuqsWFxdVLpf9ZKk/drZdY2Njqe3eC1ljtL6+PjDWY2NjWzofZVlfX9ft27c1MzPjZw34yU9+omq1OpDm3r5MSw+GzM20+rZrdXVVhUJBk5OTfhZw8Jh9JMlIMtVqdSA9jmNTr9cHyrTb7YEyz1O73U7a5atWq6bZbPrJQzWbTRNFkZ98INy5cyfp6507d/zsA6HX65mJiQk/ObeiKDJRFJk4jo3pz7cwDDccJ1a9XjdhGCbHSBzHJooiE4ZhUsbO2VE8ePDAFAqFzPL1ej1z/tvt2GOg1+uZubk5I2mgP35fbB/898P6ZPptnZiYMJKSc4bLHUfTb0+hUBh6jEZRZB48eOAnG9M/vocdB71ez0xNTRlJqce03b7tvx2vtLbvllHGqFqtml6vZ0y/jzs95/Z6vYE6s8RxPDA3rF6vl8wxtx02PattWfVtx4MHD8zc3JyfDBxYG8/Ie8geoO7JzD+xph3Ez5s96SrlC2yrJw5bV9rJ/nmJ49hUq1UThmHST/sKw9BMTU0dqP3RbDaNJHPt2jU/K5eUEizX6/XMORJF0YYvGjuvst5nscHwtWvXUsvPzc2ZO3fuZNZXr9dTg+nNjuFCoTCw/0bpUxzHZmpqyvR6PRNFUWpw4rt27ZopFAp+8oBms2kKhcKGIK5arZqJiYmhQcnU1JR58OBB5v6yc9WtY2pqakNgulu2M0Y2SBqlbBo/ePP3oytrnNrttpmamhoIdk0/qBo2Vln1bZUbvPV6vW2PBbCfNp6R95ANCuwBGkXR0ADODZzCMEz+b8u+t9zAww2o7MnTvvxt+fztpaW7oijKrNv+X63bLrce93NuPe12O3lvr0q4dQyr33LrU8qXrsu2yV6lcK/AtfsBtr064wcZo0jrc9pr2Jf9Xrlz505ypUIpV4ZHsRv9i6LITExMJPswjmMThmHmeNfrdVMoFJI67VUg94vTtmsz1WrVXLt2bdPyWfk23Q3GsoI6y84pN6gZpU+uUYOTMAxHKucHcaMEb66sQMLW46r3r2jutVHHyJ5Xs+abde3atYHzkT3n+eeitHGwwjDccK40/TGp1+umWq0OBNzNZnPocenXZ/ejHXN7NTgMQ9Pr9ZL8QqEw0F//f15HGTfgedv7s4jDPUD8k4Bfxp7I7cnOBlQ2KHMDLDews1+Ctpw9+G09/vYsv3wYhsmJKC2Aswd8HMfJZ22b7QnNBkC23rh/q1gpJzlbv/2c+ieRtL5l1W+c4M22xbYziy1vvyjdvto67EnQb3Oezc3NbTiJP0/2Npx9Zc1Ty14xsy//S87eFrUBaqFQ2PCldOfOHTM1NWXMkADNGpbfbreTIF/SpoFPVlC1WZ9cowQn9st6WFtctvzU1NSmffBlBXBR//a4y54D7PG1V0YZI9Ofe3YeZLHHi21zFEVbPnbu3LkzcN52TUxMmAcPHpgHDx4YOcHk1NRU5rHg1xf37yS45892u51cYZybm0v+RyNrDgJ5kn5G3iP+iTna5Aqc2UEAZwMTW3/a51x+efvev3JmnC8zW5d9b4M0t6xvswDOHw+/b8PqT8uz/cg6Wfn5wwK4zU7ye8G2ZdTXKOw4+bfMnpdr164NXIGzAVHWPmv318jZ/RPHsZmYmNgwp1w2OLLzy37GBilugJZWT1YA1+v1TBiGyRejvZ2WFTjZ49DP22qfRglOwjDMvIKXxR4Pth2j2k4AlzX//Dmd9tqs72bEMar3r5b6+8Nlj5etjolvamoqtT29/jpBK+wv2zD9W+32uPBl1WcDcdteG8C5ZcOMK4FAnuzLU6hZrly54iftmrW1NT9Jcp7o9Nny09PTCoJAy8vLkqQnT554JaXHjx9L/bqCINDZs2el/lOiaeW34qWXXvKTBgyrf1jew4cP/SRJ0ne+8x2p/xtr/g9w/ulPf1Kr1dLCwoIKhYLee++9gfxRDHsC0X1l/bxF/38yRn6Nwv7G0yuvvJJs332CcHV1NXlCL+0pPtdO+ydJ3/72t/XDH/4w+VHiyclJVatVffjhh35Rqf+bVW+//XbypFyxWNS///u/a3l5OfOpzXfeeUcTExO6ffu2JGlubk6fffaZjh49qsCZw4Ez90fx4x//WKVSKfkZifHxcX3wwQd69uxZ6m9pXblyRdVqVePj4wPp2+nTMK1WS3Ec61vf+paflen69eu6f/++pqam9K//+q+pT9xu1Ze//OXMek6ePOknSSPO+c2e9BxFq9XSw4cPtbS0tGF/uG7duqUwDHf0ZGa329XNmzd18eJFP0sff/yxLly4kLz/t3/7N928eVOrq6saGxtL/bHuYfXdu3dPFy5cSNr7P//zPyoUCsmYdbtdxXGsf/iHf/A+CeTLcw3gJicnValU/OQBx48f95N2xP5kic8+vl6v1wdOlGknLTfIcssuLS3p2LFjSd6wL+3t2m79J06c8JMkSa+//rra7bYuXLig73znO8kXuSS98cYbunLliiqVij777LPML5xhJicnN3z5pL3Sxnmv3L17d8NP2bg/YfONb3xDN27cUK/X082bNzcEtq7d6t+f/vQnP0nPnj3zkxJffPGFnyRJ+vOf/+wnJdz6Wq3WQPvsT+XY91uRFaD4bex0OorjWO++++5AuuWXt4b1KcuNGzdUrVZTv/zTtFotvffee/rVr36lVqulU6dOqVwuZ/ZtVK+99po+++yzgXoePnyoiYmJgXL7rdVq6caNG5qfn9f4+LhWV1czf0rk7t27G37eY6t+/OMfa2pqKnV/3Lt3T1//+teT9zYom52dHQjsXMPqW1lZ0WuvvZa8//Wvf63Tp08n7z/++GNNTEwMDVqBXPAvye0le/l/2NoWW8Ze/vZvfdr1X5vdQrWfs5fN7W2LrMvmNt8dEntL1L+Fapx22vrj/voL49yGcdtob6PY7UT928e2n36/rbS+Davf5tmy4SZr4HzuQwxZa1zc22TuGBw0dqx9c3NzJuw/FGPZW0h2DY5bdq/7F3kPMdhbqPb2n+2HnRt1b8G/vd3oLpa3t89sv+wtVH9+WXa/Z92uysq3x0baLVS/bBRFmbfhR+mTa2JiIvM8YtuUdYvSZ2+5+eWrW3iQwc4pXxzHpuD9jEhhn9ZeZo2R/ZkRt1/1/kMEaWzfer2e6fV65tq1a5nn0SxZfba3T/08uyY0aztpnzEZyyMmJiYG+jY1NWWq1ap58ODBwMM3QN5s/HbbA25w5L7STvBuvmWDEPUDH/tve3JKC3KME8TZV9bJwPLbacu7ae56FjfdP3m7bZYXRNg0P+BLK+vW425jWP3D6tuM+7msz7oBxygLoJ8XGxT4ev2fWLB9jJzfAbNf/tawL7bd4gfEobfA2g/gbJqdAzZA8L+QJ5wnbCcmJlK/8Iz3O3D+PG56T0kXCoWB8TIpT/NO9X9aw2UD46wA0ozQJ9Ofe+7cn5iY2LDObWpqauA43YzfH1d1k9+Bm5ubG+h76Dz8ZNnF9jZ/r4OGzcbIba/7yprn7vHiz81RNJvNDfPKcueWK+t/GMwm9dlg3LLr3/xjR86DW0BeBWar90sOoG63m9wajeM49bI6dsf6+rqOHj0qSSoUCrpw4YLee++9bd1e3Wt2/dp3v/tdPyvT6uqqXnnlleQ24uXLl3XkyJFdWXMEHEblclnnz5/ftWNot+sD8uq5roHbKbuA3EXwtrfsAxx37tzR06dP1Wq1DmTw1u129ezZsy0Fb+ovLC8UClpcXNT6+rpu3rzJ30UEtqnb7Wp5eTn1YYPt2O36gDzLdQBnF4bbq2/D/mYpdsfJkyc1NzenN954I3l6c6cLvfdCsVjU/Py8nzyS+fl5vfXWWzp69KimpqY2fQABQLphDxtsx27XB+TZC3ELFS+29fV1vf/++1pYWJAkNZvNTZ9eBgDgRZbrK3A4HP75n/9ZJ0+eVK/XkzGG4A0AcOgRwOFAW11d1fLysr797W/r6NGjyQ/urq+vq1wub/gRXgAADgMCOBxof/7znzUxMSH7A7N2XdutW7dULBaTp0WH/dguAAAvGgI4HGhf+cpXND4+riAINDY2pvv370v9X+23f13i/Pnz+vzzz71PAgDw4iKAw4E2Pj6upaUlGWP09OnTZP3bkSNH9Lvf/U6S9Lvf/U5f/epXvU8CAPDiIoBDLl28eFFxHCsIAv3xj3/U66+/7hcBAOCFxc+IAAAA5AxX4AAAAHKGAA4AACBnCOAAAABy5v8DhfuscNapUKYAAAAASUVORK5CYII=[/img][br]

sjhd

1. Crear una esfera de radio 5[br]2. Escriba el punto A(0,0,0) o A(1,1,1)[br]3. Ingrese los puntos B(3, 0, 0), C(-3,0,0) y D(0,3,0)[br]4. Usea la función vector para crear los vectores AB, AC, AD[br][br]

1. Crea el punto A(0,0,0), B(2,0,0), C(4,0,0) [br]2. Crea la esfera de radio 5 (dieléctrico)[br]3. ingrese k=9*10^9 (constante de proporcionalidad)[br]4. Ingrese e_c=4 (constante de permitividad)[br]5. Ingrese q=10^-5 C (valor de la carga)[br]6. Usando la función vector, encuentre dibuja el u=vector (AB)[br]7. Use la función v=longitud(u)[br]8. Defina r_n=v/100 (convierte la longitu de cm a m)[br]9. Calcula el campo eléctrico E=[k/e_c(r_n^2)]*q[br]10. Usea los pasos 6, 7,8 y 9 para el punto C

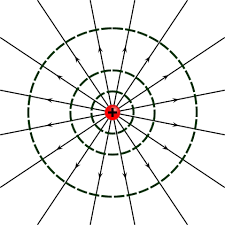
1. Crea el punto P(0,0,0) [br]2. Crea la esfera de radio 3 (dieléctrico)[br]3. Crea los deslizadores e,f,g desde -3 a 3 con paso de 1[br]4. Crea el punto Q(e,f,g)[br]5. Ingrese k=9*10^9 (constante de proporcionalidad)[br]4. Ingrese e_c=4 (constante de permitividad)[br]5. Ingrese q=10^-5 C (valor de la carga)[br]6. Usando la función vector, u=vector (PQ)[br]7. Use la función v=longitud(u)[br]8. Defina r_n=v/100 (convierte la longitu de cm a m)[br]9. Calcula el campo eléctrico E=[k/e_c(r_n^2)]*q[br]10. Ingrese la constante e_0=8.854187817×10−12C2/N/m2[br]11. Calcula el flujo elèctrico [math]\Phi[/math]=q/e_0[br][table][tr][td][br][br][br][br][/td][/tr][/table]