IM Geo.2.7 Lesson: Angle-Side-Angle Triangle Congruence
What do you notice? What do you wonder?
Assertion: Through two distinct points passes a unique line. Two lines are said to be [i]distinct[/i] if there is at least one point that belongs to one but not the other. Otherwise, we say the lines are the same. Lines that have no point in common are said to be [i]parallel[/i].[br][br]Therefore, we can conclude: given two distinct lines, either they are parallel, or they have exactly one point in common.
Two triangles have 2 pairs of corresponding angles congruent, and the corresponding sides between those angles are congruent. Sketch 2 triangles that fit this description.
Label the triangles [math]WXY[/math] and [math]DEF[/math], so that angle [math]W[/math] is congruent to angle [math]D[/math], angle [math]X[/math] is congruent to angle [math]E[/math], and side [math]WX[/math] is congruent to side [math]DE[/math].[br][br]Use a sequence of rigid motions to take triangle [math]WXY[/math] onto triangle [math]DEF[/math]. For each step, explain how you know that one or more vertices will line up.[br]
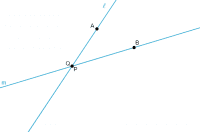
Lines l and m are parallel. a=42. Find b, c, d, e, f, g, and h.
Quadrilateral ABCD is a parallelogram.
[size=150]By definition, that means that segment [math]AB[/math] is parallel to segment [math]CD[/math], and segment [math]BC[/math] is parallel to segment [math]AD[/math].[br][br][list][*][size=100]Use the applet below. Sketch parallelogram [math]ABCD[/math] and then draw an auxiliary line to show how [math]ABCD[/math] can be decomposed into 2 triangles.[br][/size][/*][*][size=100]Prove that the 2 triangles you created are congruent, and explain why that shows one pair of opposite sides of a parallelogram must be congruent.[/size][/*][/list][/size]
When we have 3 consecutive vertices of a polygon A, B, and C so that the triangle ABC lies entirely inside the polygon, we call B an ear of the polygon.
How many ears does a parallelogram have?[br]
Draw a quadrilateral that has fewer ears than a parallelogram.
In 1975, Gary Meisters proved that every polygon has at least 2 ears. Draw a hexagon with only 2 ears.
IM Geo.2.7 Practice: Angle-Side-Angle Triangle Congruence
What triangle congruence theorem could you use to prove triangle [math]ADE[/math] is congruent to triangle [math]CBE[/math]?
Han wrote a proof that triangle BCD is congruent to triangle DAB.
Han's proof is incomplete.
[list][*]Line [math]AB[/math] is parallel to line [math]DC[/math] and cut by transversal [math]DB[/math]. So angles [math]CDB[/math] and [math]ABD[/math] are alternate interior angles and must be congruent.[/*][*]Side [math]DB[/math] is congruent to side [math]BD[/math] because they're the same segment.[/*][*]Angle [math]A[/math] is congruent to angle[math]C[/math] because they're both right angles.[/*][*]By the Angle-Side-Angle Triangle Congruence Theorem, triangle [math]BCD[/math] is congruent to triangle [math]DAB.[/math][/*][/list][br][br] How can Han fix his proof?
Segment GE is an angle bisector of both angle HEF and angle FGH.
Prove triangle[math]HGE[/math] is congruent to triangle [math]FGE[/math].
Triangles ACD and BCD are isosceles.
Angle [math]BAC[/math] has a measure of 33 degrees and angle [math]BDC[/math] has a measure of 35 degrees. Find the measure of angle [math]ABD[/math].
Which conjecture is possible to prove?
Andre is drawing a triangle that is congruent to this one.
[size=150]He begins by constructing an angle congruent to angle[math]LKJ[/math]. [/size][br]What is the least amount of additional information that Andre needs to construct a triangle congruent to this one?
Here is a diagram of a straightedge and compass construction.
[math]C[/math] is the center of one circle, and [math][/math]B is the center of the other. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAR0AAADhCAYAAAD1TWGtAAAgAElEQVR4Ae2dC9hWUxr3hVQOpYOiBqVQDpUIUUrOKmqqIeTQaMb51AGloVIOg0xjQgdSDVJOpdA0hGKIKBOdNI4jJseiCOu7fuv71vvt9/Ec9n72ae297/u63ut53+fde6+1/ns//2ete933/95KiQkCgoAgECECW0XYljQlCAgCgoAS0pGHQBAQBCJFQEgnUrilMUFAEBDSkWdAEBAEIkVASCdSuKUxQUAQENKJ8RlYv369WrVqlXrllVfUnDlz1JQpU9Sdd96phg0bpi6++GJ1+umnq+OPP14dfPDBqnHjxqpmzZqqatWqqkGDBmq//fZT7du3V6eeeqo677zz1MCBA9Xo0aPVvffeq2bOnKmee+45tXTpUvXRRx+p77//PsZRStOCQGUEhHQq4xHKX19++aV68cUX1V//+lfVr18/ddBBB6mtttpK7bDDDmq33XZT++67r2rbtq065phjVI8ePdS5556rLrvsMnXdddepW2+9Vd1zzz3qwQcf1MQ0f/589dhjj6nJkyersWPHqhtvvFENHjxYXXDBBeqMM85Q3bp1Ux07dtRtNG3aVO2yyy6qWrVqup2TTz5ZDR06VJPSihUrQhmrXFQQKIWAkE4phDz+f82aNerJJ5/Usw5mKhAKBLPXXnup3/3ud5pEmIV8++23Hq/s7/BPPvlEPfHEE5p0mD3Vrl1b1apVS3Xq1EldccUVauLEiXrGFXW//I1Kzk4iAkI6Pu/aM888owYNGqROOukktfvuu2uC2WOPPfSMhVkIyyY+8Dbav//9b72ku/LKK/VSjRkRy7dDDjlEnXPOOXomtXbtWhu7Ln1KMAJCOmXcvAULFmiiwa/CLIaZw9VXX60eeughleRly8aNG/UyEL8SpMPybNttt9V+owkTJqj//ve/ZaAlpwgClREQ0qmMR8G/Xn31Ve3gbdOmjSaaDh06qFtuuUW98847Bc9J+j9++ukn9fjjj6vf//73qn79+mqnnXbSzu2pU6cq/FRigkA5CAjpFEGN3R92hI488khNNK1bt9bOXQgoa/bVV18pyAa/1Pbbb68d1Di8Z8yYoTZt2pQ1OGS8PhAQ0skBb+XKleqOO+7QO0ksnVhi4Ghl10js/yLw4YcfqnHjxmk/Fhjhy7rwwgvVU089JRAJAiURENL5fxC9+eabetuZDxFLCZYULC1YYogVRoDlJctMlptghxOanTAxQaAQApknHXZwLrnkEu0wJQiP4DqWEmLeEWDZSbzQNttsow4//HAdS+T9KnJG2hHILOmwy8SyqUaNGjriF7IRCwaBt956SxN59erV9Qxo2rRpwVxYrpIKBDJHOgTvEVfDToyZ2aTiTlo4CGaREPuOO+6ojj76aDV9+nQLeyldihqBzJDOBx98oK699lodiStkE+1jhnMeot95553Vcccdpx599NFoOyCtWYVA6kmHaGASKHEOC9nE++y99957mvjJByOCm3QRsewhkGrSeeCBB3R2tpCNXQ82W+58EZDsSuQzZCSWHQRSSTrIObDlzRbun/70p+zczYSN9D//+Y86++yzdZyPbLMn7Ob56G7qSOfvf/+72nvvvXUCowT0+XgyIjwVwvnNb36jpTnw/4RtY8aM0V9IYbcj18+PQGpIZ926deqPf/yjfpiGDBmitmzZkn/E8q6VCCBmhh4QS6677747tD4Sg4VDu1WrVur5558PrR25cGEEUkE6jzzyiGrRooU67LDDFFITYslFAMEylBHJ8WLLPWi7/vrrtR8JoTMhnaDRdXe9RJMOcp9EE+O7QT1PZDnd3XTbjyK1onfv3jqpFLXFoAwfErMcXpF5hYDEokcgsaSDZOeBBx6ot8El0TD6ByeKFiGcunXrqt/+9reKKGe/xk6ZIRpeze9+ryvne0MgkaRDkB+zGxTvRF7T2w1P2tHLli3TKozMUO6///6yu8/shmeGCOkbbrhBy7SyxBKLHoHEkQ5brKQwoOMilh0ERo4cqUkDCdhyDIIxSypmOMx6hHTKQdL/OYkhHWY0VEvYc8891T//+U//I5crJA4BZFSZraDd48VwGCNC71QP4D2uVcgIWHz22Wd15QxmWH/5y1905Q1kaS+66CLVt29f1b17d/1MEl2N45vYMGZSVPFA7gPNIYTPkEghfON///tfoeYy9X5h1C2C4d1331XNmzdXKPcx3RbLLgL33XefJotTTjnFNQjMaIjNyTUn6SDLgXhbz549VcOGDXUbKCQiUEbJIHLGqO7BxgXLM/xNaGLPmzdPp3NMmjRJEw0bGpQZon8oTlINpF69evp6tMdzzP85Psl62rlYevnbetLhG4LlVOfOnUVQy8udTfGxJIxCCKS3bN68uehImdGwrHLaN998o8mCAoaIjxlS2GeffdT555+vK2S8//77zlMC+f2ll17S8rfUH+OZhoQoTdSnTx9dZPFf//pXIO3YfhGrSYfcKW5Mr169bMdR+hcxAuxmEc9DMKHb3K3XXntNbz5wHs8Vu58ElPKcrV69OuIRKPXyyy/r2RXhAY0aNdJ9atmypa6NlubKG9aSDoLoPBj9+/eP/GGQBpOBwIYNG3TKC88Js4hCxsyIZRPHUUmVqqnLly8vdHhs70NCAwYM0CkhqCJcddVVasmSJbH1J6yGrSQd6njzgNx+++1hjVuumyIETFkgqlMweyGNgrQY/DiQDOWb+R+FD5NgOLyJzEb4jM8By6+k9N0NvtaRDrW8Afrpp5920385RhDQCJjChzw7/OAzMbMaYnSSapSgZglInBIkhAM66WYV6eDw44EJw4mX9Bsl/S+OAKWcDeHwStZ6mgy5lttuu03vpFFRNskKCtaQjokyLrUbkaYHScYSDAJz587VMwEn6fzhD38I5uKWXQU/lvmsXH755Yks9WwF6UyZMkV/S7ndhbDsOZDuxITAp59+qi699FK13Xbb6eenS5cuqmrVqhUzHuK70movvviilnxlyz1plUxiJx2ii/mGeuGFF9L6fMi4QkCAIMFmzZppxzHPj/ngERF8wAEH6K103v/ss89CaN2eS44dO1btuuuuqmvXrgoiSoLFSjpU1eTBQO1PTBBwg8Dbb7+tZS8gHOK3nITD+ZBPp06d9Ps4lwn4S7ugGzFG5513nh4zVTdsH29spIOzmKhSYibEBAE3COA8bdKkiV5Skd+USzhcg2976s/j0znhhBP0bCg3ItlNW0k8BjE7ZnksM22e4cVCOiRvUvP6sssuS+K9lT7HgACzYUiGRMo///nPeQmHbpFUSVnjhQsX6mNI1iTZMyvPGsUkjzrqKNWuXTtlq08rFtJhWkyEqJgg4AYBEjEhnL/97W86YDTfDMd5Hb7tyRDHv8NSi2ROziFRMyvG7I7KqkQ522aRkw5pDWgZf/7557ZhIf2xEAETnY5EhKniYJzGhbpLLhPHUmiRWc/MmTPV7NmzNfEgUZEVM34e25Q1IyUdtEgI2sKBLCYIFEMAZyhLcFIYmKlAFqVmOOZ61DozOXvEtPAlh1HqhmtAYFmxgQMH6jGHWWHDK5aRkc7kyZP14PnGERMEiiFA3XnIgWzwL7/8UrEt7JZwuC46N+3bt9dNcD7LDEM0o0aN0oGEQWguFxuDTf8zcXAXXHCBFd2KhHQoI0sQ0/Dhw60YtHTCXgSM/wWxK+yuu+7yRDicw0y6Tp06FYMcMWKEQjLCGPl9iL1nyZYuXapxRH0zbouEdJBxtGGwcYMt7RdH4OOPP9YfDHZeMOQ+vcxwzNU3bdqkateuXaEyyd+77LKLGj9+vD4E9UmqTARZ3sa0bfsreKIzHqeFTjpsdW677bZF9U7iBEDatgcBtraR98SQdiiHcMxojjjiCPXwww+bP/U2O+WmjUE4EFEYBf1MGza+Eh8Hrvi64rJQSQf1MyJCWUeLCQLFEEAHB9nQH3/8UUcV+yEc2mF2jUPZaYj6O3ev2OVCUD1rRsoR+LJ0jcNCJR0cV0SFigkCxRAggnbrrbdW+P4mTJjga4Zj2iGAMFfmlg8Zu6c///yzPoxKojirbdrZMf0P+9U4lylaGbWFRjrTp09XNWrUUFkRm476xqWlPcrJ8K2LAxmBKr8zHIMLsSnkXuUaDuqbb7654m2Wcegsr1y5suK9rPxCLTGWtGAfpYVCOgT+7b///jpkPcrBSFvJQuCmm27SJPPkk0/q6p1BEQ4oIJPC9b7++utKoEBs7Gxt3Lix4v0zzjhD8ZNFo/oFS1uc+FFZKKRDbSCmzGKCQCEETC4VMw1T9aNUpHGhaxV6Hx/OggULfvVv6lg565ivWrVKL7sIHsya/fDDD+rYY4+N9PMaOOmgvI8+7euvv561+yfjdYkAM2F2qciFMr6FoAmHruBPZNs91x588EG99HdW3IRwKKyXRSE5SBe513JLNufiW+rvQEkHFftWrVrpWj6lGpb/ZxcBQvNJTTBR6mEQDuiS8ImyYD5jSx3tGacRv0KN8ywaM058sNQGC9sCJR22KLt16xZ2n+X6CUbAbNdS3ylIH04+SCCzQkGp1BenfXbMjFE1AqcyPqYsGpnpUWgPBUY63Dy2H23LaM3iw2PzmCmpiw8hbMIBAwS9IJFCBiHhf3TasGHDtPaw872s/M5OM3rTSIiEaYGRzpAhQxQ5LWKCQCEEiIcxdcPDWlI520Y9D2mLQn4aNHcgP+d2OV+eRCrjm8yi4Wdr2LChQgwsLAuEdLipbENyE8UEgXwIsCVLqdwoZjjO9hH0YilVyBA0J3rZaaQIHHfccc63MvM7u1n429DiCcsCIZ3BgwdrseywOinXTT4CJ510UuSEA2qkOhRLw2EJBhE6pS74EqWiJgGuWbQnnnhCY4JESBjmm3SYmtasWVNRSkZMEMiHAH4SPtjXXHNNvn+H+h6bG2eeeWbRNiCm3OBAdrYo45tVo5Qxs8QvvvgicAh8k86VV175qxsWeC/lgolFgAoFEE5cu5p8WxMMWMwWL16s++jUE+bLFPGvadOmFTs1tf9DSI2NoTCqtfgineXLl+syMlIoL7XPnq+BGcIhmTOuygQIelWrVq3kOIjRyd0IIc6nQ4cOJc9N6wGENbRt2zbw4fkiHQKv4hYEChwRuWAgCBjCYYaTu3QJpAGXF/nuu++0oBezmWKGrg4zMqebgPeqV6+ugxiLnZvW/+HnApM5c+YEOsSySQf5Q+pGO6ekgfZMLpZYBAzhsC2OcNasWbNiHQvRx5QhLmX4MU488cRKhxHHc/jhh1d6L0t/4A8799xzAx1y2aSDJEG/fv0C7YxcLPkIGMIhrJ7fw5iee0WJLXFSL0oZu1Z8szsDXPm2J9Yni8mg4PX0009rFwrR2kFZWaRDMmeVKlUiydMIaqBynfARcBIOrZ1yyinqtttuC7/hEi0g6EUktBtjY6Rjx46VDkWMjnI4WbXOnTsH6lAui3TYAi21DZnVG5TVcRvCMSp8+EOIdfnoo49ih4SZS+PGjV31A4ldNL1nzJhRcbypUOGcAVX8MwO/UJo5yBlrWaTTpk2bzG4lZuAZ8zzEXMLhAhRWxEdig61evVovm1BBcGOk9Bx66KGVDmUXC5dCFg3dalQYg3IoeyYdRJFIeQgjaCiLNzTpYzaEk6tbs+uuu6rnnnvOmuEh6PXMM8+46g/khCYUWj/GbrnlFq23QzmbLNro0aNVz549Axm6Z9IhUlOWVoFgn/iLGMLJzUomWxlRKJsMQS8v/iX0g5HxNIaIO05m57LL/C8Lr9QKg7iDMM+kwzQrq1GaQQCelmsUIhzGR5kX20q7EOjnZbd18+bNOkHVmQ1P/ljQ28dJeh6opBGEIqgn0mF6KkurJD0m4fTVEE6huknMhMMIn/czGsjDa7wNM6NmzZpVNMsSEtkL6qNn0bp3755X/tUrFp5IhwhkWVp5hThdx5ciHEbLTpFN/hz6hC+ScitejbHceeed+jS0drbffns1depUr5dJxfFoKAcx03NNOlu2bFFNmjSRpVUqHp/yBmEIp1gNcJNO8O2335bXSEhnffrppzrIz6s4Ff4qRK1++ukn3TOWjaeffrrrXrLdjDCW+QkyyM51JwI6kJWO29CDYk26Jh00NmRpVQzKdP/PDeGAAOkGudvNtiCDVAOlb7xaixYtFDW6MGY57GwRz+PGmF0h9k7JG15xRj///PNuTrXumPXr1+v+r1ixwlffXJMORblkaeUL68SebAhn7NixJcfA9Pviiy8ueVwcB6CbM3ToUM9NQ6S1a9dWGzZsUGyno4BI+eNSxqwGknGaISDne0n6HeJm9ubHKiNS4EpMlRG4ll2rAgCl+G1DOOxIuTGm3xTPs9EQ9MqVr3DbTwJiicTHyOVyUzWBD2duSgV/jxkzxm2z1h2HjKlfv44r0kEISZZW1t3/0DvklXDMN3tc2jmlAKHIHkX+yjE+A8hcUCgQzWVSJdauXVv0UpdffrlixwcnNs5ofod03EZGF714TP8kzcWvX8cV6Zx11lmytIrpJsfVrCEcs3Pjph9z587Vcidujo3jGGJMcpc7Xvpx5JFH6mx1nMpNmzZVpZabEIxZTvE7hSgRFUuyLVy4UGOITlG55op02LUyiXzlNiTnJQeBcgiH0eFkLVZnKm4EcBPgmyGBsxwzguXvv/++6tu3b0kBOwjOuVvFcsvvLKGcfgd5Dk5kxuUsUuj1+iVJh6kyjYhYl1dok3m8IZxy/A6cg6PRZkPQq9iWf6m+UygQRzmBg8W0l5nR5MYFsWvlZ6ZVqm9R/J/674zBz4ytJOmwDqbaA/VwxNKNgCGcO+64o6yBXnfddapTp05lnRvVSTiBL7roorKbmzdvnv7QsaOFX+ebb77Jey0ImCWVMfw4+HRYbiXdIJ358+eXPYySpENNqyyLU5eNbMJO9Es4DBfph6AykcOCD0Evv8SI7jN+ThQFqZuVzyAXllK0xQ/aQryXZCeyGSdVWv3UBCtJOlQ6zK33bBqX13QgYAjn9ttv9zUgonVt0dApNBD0momz8WMvvfSSnu00b95cFco/Y/nBcoofP0sRP/0M61x2AHOlTLy0VZJ0YLWs6sN6ATKpxwZFOIz/mGOOKSv4LkrsjCPUrx4UBLvXXntZT7JhYMsuHtIf5VpR0kFDg/Ubr2LpQ8AQjhedmWIotG7dWpXrDyp23SD/98svv2hdGATH/ZjZfmdn12s+l592bTgX7WukQsq1oqSDs4ygQLH0IWAIBx9HULb77rtXUtsL6rpBXwdBrxEjRvi+LPoyfCnzM2nSJN/XS8oF0CXCp1WuFSUdvPxZrudcLqi2nxcG4TBmZB+C0tENE0O+pb1kiufrCzIPhnDMaxqcxPnGmvsem0sImpVrRUnnsMMOc1UvqNzG5bzoETCEE4bIVlJIh5pcLVu2dAX+xx9/rGs/MSNk9+nggw9W22233a8IB+JZt26dq2sm/aBQSYca0DykYulAIEzCAaGkLK8QGCPGxmlEKxMAO378eHXZZZfpGT4qgZAJ293t27fXIQHo67BNjnogcTdmluMlXcTZbhJ/D2159cYbb2hACfkWSz4ChnCoahCWJcGRzNghna233lpHFkMcSJJCHhSQZAZE7XWqH8yePbtSGkMubmjqcB4Z6Fmy0BzJaMo2aNAgS1haP1byeJAV4MPNw07QmRtBKEM4N998c6hjtG3LvNjSqGrVqhrHa665Rku2LF26VP3888+e8Fm0aJFOcKXcTpYstC3za6+9VpFnImYHAgSYMc1HgY7fcVoiseBMKMzX06gIh7bjCg4stTQyhfKcSyMEvSgh7MfQlyJQjqXa999/7+dSiTo3tOBAktpOO+20RIGR1s5CMITUe03CNIRjpDbDxieKNIjly5frEHzyvJxLI5ZLZmnEeEstjRD0Yuvcj7HtfuKJJ+qwEhvKJ/sZi5dzQ0uDIHXfT2Kcl0HIscURgGzQYvFiURMOfQsy4ZMPMQF8ZtcIv4nZNaLoW9euXZWfpRGzFBzffgwVPYiWLwSWZ1kxlvahJHwix2jkGbMCpq3jJFvZyyzHEA7O0CiNPnqVtnAujShxRFyY2TVC+8Ysjcj1MbtGQYzptdde034xP9fCp0boATMs20ru+BlXsXNDlbbg5mdpG7AY0HH/D10WNw5j+mkIZ9SoUZF3u5SIF0ujhx9+WM+I8i2NEP43S6Owd02//vprLehFCeRyjRkXZYbZTp85c2a5l0nUeSZ3LRQRL4KgslpUzLangOmsG9KJk3DAzMiVFlsasRQxSyPKwZSzaxTU/UHQy63gfG6bP/74o54pkYN18sknK2f54dxj0/R3qHKle++9t36I0gRYUsfiZnllCIfw/Kgsd2nUrl07/UGEJM3SCL9g0EujoMaHoFe5olorV67UYyVIsE+fPjquJ6h+2XydUIXZidEpV0vWZtCS2De0ddkuR6MXYzfLqdESBeFQubPQ0ggnt1ka8dz41eWJ6h7hj2nbtm1ZzeHkrlu3rj4XDaGBAweWdZ2knRRqCZoaNWpkLmXf5gfA7GAxi+CH8iaYIRw/+ibOcTuXRmeffbaOtjW7RmZpRAxXoaWRzcX2nOPkd0h8xx13zH3b1d/M3g455BB97KBBgxQfxixYaMX2zHqVqaOYvQgYwilHpsEsjfBF5Ns1Ouqoo3TIhNelEbMyW8sK597Jd955RxM45XK9GkRDgCEG4bspvue1DduON2WF/dY1y5tlzsUJthKzFwEvhJO7NKJmE7Ml7rFzafTUU08pv7tG7FBxbUjNdqN+FTtQ5chx9OrVS5FtjeGMZgcr7fbMM88EUkInL+kQWk+shJhdCLAcIHSfcH4+2MOHD6/UQb9Lo0oX8/EHy7CkxK0QlUxqiVdjdxeJDIzZ3X777ef1Eok7nk0Kltx+LS/psI2J6LSYPQggKQrRmB++afMtjVB6zF0aRS0uxYMZhl5PGHcD3xhZ016N3blnn31Wn/bYY49lIjma2KpCQvRe8MtLOqjdk0kqZgcC1BwjK9oQDq/IMAS9NApqtBSzI/kzCYbPCmkLL4aoO/dg1apV+jRSArg/aTfkWRcvXux7mHlJhxDxrGmE+EYy5Aswe3GSDnIKtpZ6JtRijz32CBmRYC4PYYCrF+ODxzlbtmzRp+EToiBlmo3iDH5z1Qw+edEm1BkHm5g9CLBjwK4QD/sFF1ygEOPiIWjUqJFOHdiwYYM9nVVKQYpJ8OsQzk/RPIL93BpOfPxWxqiC6/zbvJ+mV/L4giqkmJd0Pvnkk7LjF9IEtI1jee+99yp1C7/OgQceqO8XWdcIV9lgV199dWJqQhF74iXlB8J3FizAoYxjOa1GCA2O8nJ2+fJhkpd0+NbkG3Xz5s35zpH3LESAaGG2bc1MiG3yOI32iaJmR812I97GSxVbZpqkUBjDaX788cebP1P3SimqciO384GRl3Q4kBgOZjxiyUKAWIouXbpo8iEnCEnNuIxdoaAK+YU5hqFDh2oJDbdtsM3uzHFDR8hvSRu3bcdxXOfOnQPdjSxIOnxLSWXPOG5xMG2+8sorOh+KmQ9Z0GSAR234PoL8hgyr/w888EBFHpWbNkiGJg3EGNUjUNpMo5FjRmmhUrK4XsZekHTYfXAjp+ClMTk2egQI9SfTG/JBygGnZ5TGB3TWrFlRNum5LTR1wMetMDuayJSrMUa+WVoF70jkLTcT3+CT+1qQdHCuZUWYKBeUNP5NuZQhQ4bord39998/su32G264QZd0sRlTcgwJ9mN2WMr4xoegPv3004pDe/TokUrBO5QMGGtQDmQDWEHS4VsxK8JEBowsvH733XeRbrfjUGZL2m+SYNj3hufdjVImYQC5memU3pkyZUrYXYz8+gMGDAhleVyQdFC5j6qKQORoSoMaAbZ6mdHyIQpzu53dIWY8NhvSFDjeS9mkSZN0iILzOPxWQc8GnNeP4/cPPvhAp3aEkc5SkHQIY8+KMFEcN9WmNp3b7VQ3IFM8SPvHP/6hKzn40SMOsj/5rsUXLMvOUsZOVa6MBXWg3CzNSl3bpv8jTMYXEikfQVtB0jn//PMzI0wUNKhJvR47FWFtt7PDk/thtQmnRx99VOezleoTJYevuOKKSofttttuFXlYlf6R0D9QM8CX89BDD4UygoKkc9VVV5WVfRtKL+WikSIQxnY7kdJNmjSpkIOIdEAuGsP3xAeNEivFDB3oXDH3HXbYQZUjBFasnbj+R3LxYYcdFuqEoyDpsAZPc2h3XDc1Se0Gvd1OgiqhGPgLbDNC/ck3RMismJFT5gwBQKwMskqL8blv2LBhqFLFBdHCMQaYqKuJZRsBttvRRd5pp52038NPdjuBivgLbDQijYvF25j0oLfffrui++xmHXTQQRV/J/kXfG7oYSMSF6YVJJ3PP/9ckw4yF2KCAAg4t9vRVrn55pvVxo0bPYHzwgsv6OfKVLbwdHLIB6MVXSyHigh9vojBwRi7O/369TN/JvoVn1sUfreCpAN6e+21l65ZlGgkpfOhIOBnu51dUfwG+A9sMsTHWFoUsieffFLhNHYau7ycl3TjflIBJopJRlHSIYktLSye9IfC1v6Xs93OLJptZttid5AfLeafIXgwV1GTL2ZqrCfZVq9erX1tziTWMMdTlHTuuOMOXRw+zA7ItdOBgNftdhIm+YATbGeLkeJA9DQidvmMbf+zzjqr4l+oMDCGpJdqOumkk3SoRMXAQv6lKOmQ8JkGUEPGUC7vQIBESGJZeG5KZbcTkMdxBA/aYgTEkXWez7p161bJ0cxmCzO2JBt+LETgohR/K0o6MDgPRRJkJ5N849PYd+d2O0uSQoFmREBXq1bNk1xomHghyUlWfj6DkCg3Y4zlSJJ1dMaOHatq1aoVefnwoqQDuGwHJqU2tXkY5NUeBFiClNpuJwoa38imTZti7zh9NeWCczuDrsyCBQsq3ia7HO3gJBr6SkwoKJ8TtZUknf79+1dax0bdQWkvHQiU2m5nihW7ZkgAAA+gSURBVG9DlUxmMtWrV/8V6MQq8SF1BjYS6MiOVtIMxzFjCaKGVTljL0k6dKxFixblXFvOEQTyIlBou52p/mmnnZb3nKjeRN6VD2RuUCzvO2tb4WzmuDVr1kTVtcDaYRzM6OKykqRD4b1cho+rs9JuuhDAz2PE5PHtmI0L8v7iMnKvEPTK1ZaeNm1aJacxfQ+qDlSUY2UCEURpYD99Lkk65JawlrUxgtTPwOVcexBwbreTisCXXJypEiR1jhkzphJAI0aMUGhMGaPEDlvNSTKkOxAci9tKkg4dRFXNtkCuuIGT9oNHwLndDvE0b948+EZcXBFN4NxdKUS+mI0ZI11i0KBB5k+rX8mgJ9qY0jk2mCvSgeUJWxcTBKJAgO12PiAQDx+WiRMnRtFsRRujRo3SMhwVbyilOnXqVFGGhf7RN8r92G5gR1/9JOkGPUZXpPPGG2/ojtus/BY0MHK9+BFgux15lSpVquiyvVF9cGbMmKGfdycC7FSZQgVU+KTiJcZuF6sA8xNkqRZn++X8To4bhFNKrqOca/s5xxXp0EDHjh1lieUHaTm3bATIZod46tSpo8rNbvfS+NKlS/WH9bPPPtOnobXDh5cvX6xDhw4VSyvev/zyy9X111+vX/n78ccf99JcKMeSroH2tbNUTigNlXFR16RDCr8sscpAWE4JBAGTq9WrV68KMXm2fcOoQkuQIjOb2bNn676vXLlSkw4R+q+++qr+nSBBU6LFOUBmPhSqjMvWrl2rjj32WIUz3NYKHK5JB7FuWFyWWHE9TtLu/Pnzta+FfCGWWqRX8EyGISZ/3HHHKUTYMXbX6tatq3/nvTZt2ujfIRhWALlGnyCkqI2KqqRqEOFtZmlR98FNe65Jh4uxnSm7WG5glWPCQgDVPtIPmjVrpu677z5NCEZMnkTToJYTlAmGeLBx48ZVpEa0bt26IumTZRU/uQbpRFkdlwhjdtdolxinLVu25HbJqr89kQ4JYrLEsur+ZbYzCGftsssuippaS5Ys0WTjNrvdDWiIr5tlElvjtMNMiw82SyysVatWv/LffPXVV/qYqGY6fCbRbT7qqKMUekBJME+kw3qROs6yxErCrU1/H1nykzaBw9QkXvKeqd1eLLu9FDosqSAYDD/S4MGDdekZp4gX/8/drWLJhcB72IZwGMGJhBREJb4V1Jg8kQ6NoqEqS6yg4JfrBIEA5a8bNWqkd5XInsZys9vJ9/Ji7733XkU5ZHw4LLGaNm1aQW4sn8gVcxqznMaNG/8qmtl5jN/fEYfHgQ7h8VmMQl7Ub59zz/dMOhMmTJAlVi6K8nfsCODX6Nu3r/4wIrFrhMEQjmfLnTwpr9vtxOJMnjxZ52KxJc4Hne10jDQJp4g5JIS/h2jmMIxKm8ilIjWDjnPYFRvCGIO5pmfSIcWfUiSyxDIQyqtNCLC8IXoYgmDrGDlUo9Njstt5ft1st3fv3r3CQYtPx5m3BLkwq4FoaAv/Dm0HbaQwUGcewmQHjaVjEjPbnbh4Jh1OJi9FllhOGOV32xBg5sEHFGfzPvvso59X4m0wMsSd2+2kNeQzkjrJ/4JU6tevr9AMj8qYqUFsaDYffvjhembFF34arCzSmTp1qg5P/+WXX9KAgYwhxQhQeYKlCLMfxLmcSy9ndnu+7XZmSRAOMwxeDWmFCRefLUJTKHrHctG2FIYgxl4W6dBw27ZtpSZWEHdArhEZAs7ZD4LqpArgJ2HZxewdYkFMHjLCjJYU0i5hZGjj7CbqmVUDou/4agjuGzlypFq1alVkuETdUNmkw7dAy5YtFXkpYoJAkhD45ptv1Lx58/SHm8DCevXqaXF4tJGNj4YvVSRUISJ+SJ70a8T3oMSJiJZZtqEN3adPH01+WfGTlk063ADyOwhOEhMEko4AhIDPhmoQDRo0qCAbQzq8Egl9ySWX6JkJwYn4hiAvdJL5Eib7nHgelnCnnHKK9hsxo4LUzHUgG/7P8YXqayUdy1L990U61AdiW9FZ27lUg/J/QSAJCLDNbojCvEIWkBL+IZZBlBhGb7hmzZo6J4zZEeqCZ555pqIw3/Dhw/XMxpATUqhiSvkiHQAk/DpKr77cNEEgKgScM54pU6ZE1Wzq2/FNOkgOsCXJOllMEEgLAsxOiOeBbD788MO0DMuKcfgmHUbRuXNnvZ61YkTSCUEgAAR4ppOigRzAcCO9RCCkg44HXnhCtcUEgaQjgFwpZWiSHvlr630IhHQYHOr4CFqLCQJJR4DgvDiL0SUdv1L9D4x0qIlMUt26detKtSn/FwSsRQB9Y1IenOWDre1sQjsWGOkwfgKt2CYUEwSSigDP8LBhw5La/UT0O1DSmTVrllZbQ8lNTBBIGgJkiZM5HobYe9KwCLO/gZIOHSUoimhMMUEgSQgg2kUFCHSXxcJFIHDSWb9+vc5Zue2228LtuVxdEAgQAZI/yeoWCx+BwEmHLrPluMMOOyRSSjF8yKUF2xAYP368ljtFfVAsfARCIR26jYASwtFigoDNCJB0iaQExCMWDQKhkQ5b52TU3nTTTdGMRFoRBMpAAB0dfsSiQyA00mEI5K9Uq1ZNLVq0KLoRSUuCgEsEqPBAUqet5XddDiNxh4VKOqDRv3//ikqJiUNHOpxaBBA8Rz85yVUVknpzQiedjz/+WJeARYJRTBCwBQF0cSiiJxY9AqGTDkNCHmDrrbdWL7zwQvQjlBYFgRwEKBmM2PqyZcty/iN/RoFAJKTDQCjwjuKamCAQJwLUGCeDHOIRiweByEiHms+IfUE+YoJAHAiQxEmJYJZWYvEhEBnpMMTnnntOBw0OGDAgvhFLy5lFgJk2hetEqzjeRyBS0mGoFBND6Fq0d+K98VlrnbpSSK+89dZbWRu6deONnHRAwCjt33333dYBIh1KHwJUZ2AjY86cOekbXAJHFAvpgBPZ6Mx4qLooJgiEhQCVOXnOJM0hLIS9Xzc20qGrOPRIDKXetJggEDQC1113nSYcyvaK2YNArKQDDDj2WGuLCQJBIoAgFzMcIuLF7EIgdtIBDkinVatWdiEjvUksAi+++KImnJNPPjmxY0hzx60gnc2bN2tHX+/evdOMtYwtAgSQGmWGI19iEYBdZhNWkA59Ry6Sh0XW32XeSTlN/fDDD/oZqlevnqBhMQLWkA4YvfTSS/qhkXW4xU+MpV376KOP9LOz/fbbW9pD6ZZBwCrSoVPm4ZH1uLlF8loKgddff10TziGHHFLqUPm/BQhYRzpg8v333+syxazLN27caAFM0gVbESDgj2W5iKrbeod+3S8rScd0s2vXror1+cqVK81b8ioIVCBAuRgIZ/To0RXvyS/2I2A16QDfoEGD9INFsqiYIGAQQHsbwiGXTyxZCFhPOsB5++23ywOWrOcq1N5eeeWV+nl46qmnQm1HLh4OAokgHYZuptIki4plE4HvvvtOnXHGGWrXXXdVL7/8cjZBSMGoE0M6YP3EE0/o6hIki4plC4G1a9eqY445RrVr106qNyT81ieKdMAaneWmTZuq7t27izZKwh8+t93ny+aAAw5QXbp0UZ999pnb0+Q4SxFIHOmA49tvv61OPfVUVadOHTV27FhLoZVu+UVgw4YN6qqrrtL+myuuuEJt2bLF7yXlfAsQSCTpGNxwMO+44466lMjy5cvN2/KaAgSIvyHY7+CDD1azZs1KwYhkCAaBRJMOg1i8eLEierl+/fpKlAjNbU3u66ZNm9TVV1+tZzeESzDbEUsXAoknHXM72NWqXr266tOnjwQTGlAS9vrss89qRzEaS3Pnzk1Y76W7bhFIDekwYLZRjz/+eNWoUSM1YcIEtxjIcTEj8NNPP6mhQ4fq2c21116rmO2IpReBVJGOuU033nij2mabbXQ+DlutYvYiQKR5hw4dVPv27dW8efPs7aj0LDAEUkk6oIN63NFHH6323HNPde+99wYGmFwoGASocY92EqkMw4YNU8x2xLKBQGpJx9w+HmwiWNkFEfIxqMT3SqVXllINGjRQJPRKNZD47kVcLaeedAAWjR4e9Lp16wr5xPSkrV69Wu9KcQ9OOOEE9fjjj8fUE2k2bgQyQToGZL5l2Y6tVauWkI8BJeTXd999Vwf41axZU6cxzJgxI+QW5fK2I5Ap0jE3Y9WqVYp66tTckmWXQSXY12XLlumCisiHduzYUT344IPBNiBXSywCmSQdc7feeecd/cHYbrvthHwMKD5flyxZoi666CJVtWpVdcQRR6gpU6b4vKKcnjYEMk065mbyrcwHhXrXzHxGjhyp3nzzTfNveS2BAJIT06dPV2eddZaqUqWKOvTQQ7UUSYnT5N8ZRUBIx3Hj33jjDXXppZeqJk2a6K1cpBTGjBmj1qxZ4zhKfjUIEDV84YUX6mKJbH3jIJYdQoOOvBZCQEgnDzJkMyOncP7556vddttNBxoipTFx4sTMSysQ/zR48GDVokULTcz4a2699VYlCbd5HiR5Ky8CQjp5Yfn/b3777bfqoYce0kuH2rVrq5133ln/znKCZUUWjKUmS06WTcxoeB0xYoRiZigmCHhFQEjHA2Kff/65uv/++7WUBsml1GBnecEyY926dR6uZP+hS5cu1UtLlpgQTcuWLRV5UQsXLrS/89JDqxEQ0inz9nz44Ydq3LhxWs2ODyUO1NatW6tzzjlHf1gXLFig63eVeflIT/vggw/UI488ooYMGaJlQho2bKiJZp999lGIoM+fPz/S/khj6UZASCeA+4uEJh9MnM79+vXTy48aNWrobeO2bdtq3xAOVht2xFgSkmRJCZeePXtq6VdIkxw10hKYzRBTw46emCAQBgJCOmGgqpT68ccftcAYzmd2xHC4Iq9KsBwZ1chw4oC955579IccpTxqubOsIXL6iy++cC3PSUVUlncEPVJiF1LBEU6MzF133aWL0eEUP/DAA/UMpnnz5qp3796KbPzZs2frNJGQYJDLCgK/QkBI51eQhPsGUhvkHZGIChlRUuXEE09UzIgQnMdRzczD/BA1zQ7avvvuq4+BsPCvNG7cWOeSEYRnjq1WrZpiaYSIOSTXo0cPPctitwlVRfSGICgxQSBOBIR04kS/QNs///yzwmm9YsUKtWjRIj0bmTx5si46yOwEAmH3jCUdEcD4ZETWswCY8rZ1CAjpWHdLpEOCQLoRENJJ9/2V0QkC1iEgpGPdLZEOCQLpRkBIJ933V0YnCFiHgJCOdbdEOiQIpBsBIZ10318ZnSBgHQJCOtbdEumQIJBuBIR00n1/ZXSCgHUICOlYd0ukQ4JAuhEQ0kn3/ZXRCQLWISCkY90tkQ4JAulGQEgn3fdXRicIWIeAkI51t0Q6JAikG4H/A4MKEDP6LAoDAAAAAElFTkSuQmCC[/img][br]Which segment has the same length as segment [math]CA[/math]?