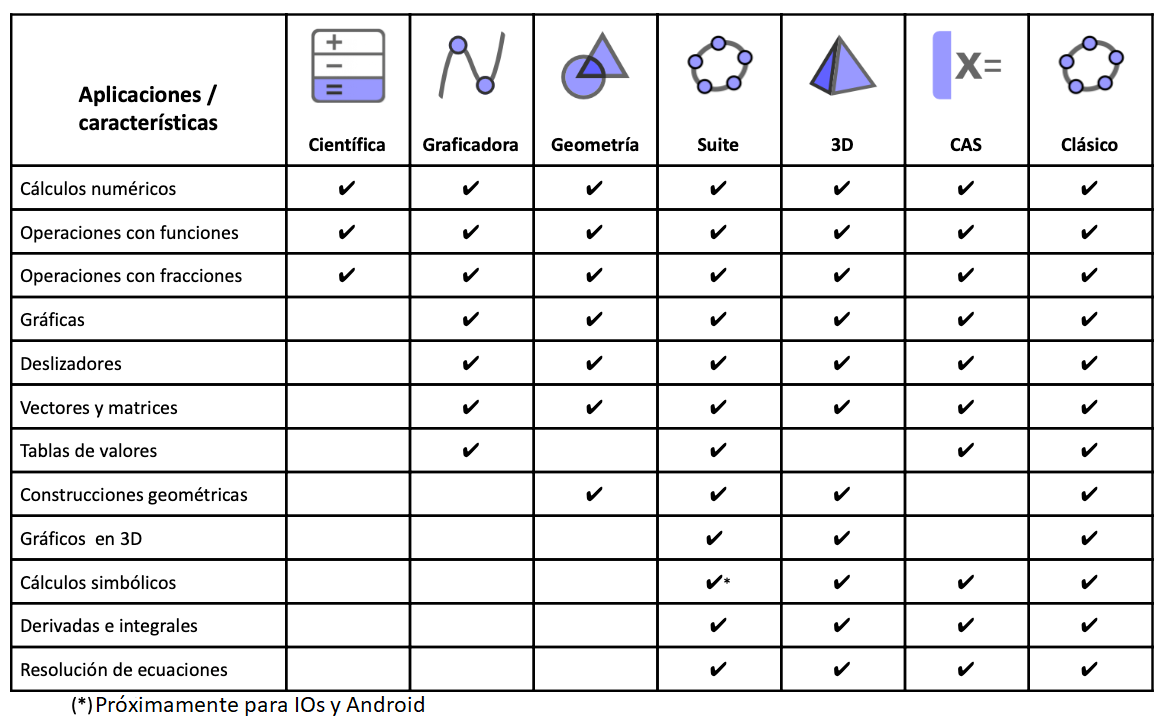
Comparación entre las Aplicaciones GeoGebra
Con nuestras aplicaciones matemáticas GeoGebra podrás explorar y aprender funciones, geometría, álgebra, estadística y 3D de maneras nuevas e interactivas.[br][list][*][url=https://www.geogebra.org/calculator]Calculadora científica[/url][br][/*][*][url=https://www.geogebra.org/graphing]Calculadora gráfica[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometría[/url][br][/*][*][url=https://www.geogebra.org/calculator]Suite Calculadora[/url][/*][*][url=https://www.geogebra.org/cas]Calculadora CAS[/url][br][/*][*][url=https://www.geogebra.org/3d]Graficadora 3D[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Clásico[/url][br][/*][/list]La aplicación correcta para ti es aquella que satisfaga tus propias necesidades y, en caso de ser utilizada en exámenes, cumpla con las regulaciones de tu región. La siguiente tabla te dará un panorama de cuáles características se encuentran disponibles en cada aplicación.

GeoGebra en Exámenes
Creemos que los estudiantes se benefician utilizando exactamente la misma aplicación GeoGebra tanto en clase, como en sus tareas, y en sus exámenes. De esta manera, podrán tener más práctica con la aplicación y, por lo tanto, serán capaces de hacer mejor uso de la tecnología en todas las situaciones. Es por esto que hemos creado el [url=https://www.geogebra.org/m/tr5sa8bn]Modo examen GeoGebra[/url] y lo hemos incorporado en cada una de nuestras aplicaciones. El modo examen bloquea los dispositivos móviles para que los estudiantes no puedan comunicarse o utilizar otras aplicaciones durante la evaluación. Esta modalidad ya ha sido testeada en contextos reales y aprobada por varios ministerios de educación en distintas regiones. Aprende más sobre cómo utilizar [url=https://www.geogebra.org/m/tr5sa8bn]GeoGebra en exámenes[/url].[br][br]
Intersección de funciones
Tarea
Crea una función lineal con deslizadores y halla la intersección con una función cuadrática.[br][br]Explora la construcción y aprende cómo crear una función con parámetros y cómo hallar la intersección entre dos funciones con la [i][url=https://www.geogebra.org/suite]Suite Calculadora GeoGebra[/url][/i]. Luego, inténtalo tú mismo siguiendo las instrucciones que se encuentran más abajo.
Explora la construción
Instrucciones
[table][tr][td]1.[/td][td][/td][td]Ingresa la función lineal [math]f(x)=a\cdot x+b[/math] en la [i]Barra de entrada[/i]. Se crearán automáticamente deslizadores para las variables [i]a[/i] y [i]b[/i].[/td][/tr][tr][td]2.[/td][td][/td][td]Activa el botón [img]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/16px-Algebra_hidden.svg.png[/img] [i]Visibilidad [/i]junto a los deslizadores para que estos se muestren en la[i] Vista gráfica.[/i][br][/td][/tr][tr][td]3.[/td][td][/td][td]Cambia los valores de los deslizadores para [i]a [/i]y [i]b [/i]y explora cómo la gráfica de [i]f(x) [/i]se adapta a los cambios.[br][/td][/tr][tr][td]4.[/td][td][/td][td]Crea una función cuadrática escribiendo [math]g\left(x\right)=x^2[/math] en la [i]Barra de entrada.[/i][/td][/tr][tr][td]5.[/td][td][/td][td]Usa el comando [math]Interseca\left(f,g\right)[/math] para crear los puntos de intersección entre [i]f(x) [/i]y [i]g(x). [/i]Los puntos de intersección [i]A [/i]y [i]B [/i]se muestran en la [i]Vista gráfica[/i], mientras que las coordenadas de los puntos se muestran en la [i]Vista [i]Algebraica[/i][/i].[/td][/tr][tr][td][/td][td][icon]/images/ggb/toolbar/mode_intersect.png[/icon][/td][td][b]Nota:[/b] Puedes encontrar la herramienta [i]Intersección [/i]en la [i]Vista herramientas. [/i]Actívala y selecciona las dos funciones para crear los puntos de intersección. [/td][/tr][tr][td]6.[/td][td][/td][td]Mueve los deslizadores para [i]a [/i]y [i]b [/i]y explora cómo los puntos de intersección [i]A y[/i] [i]B [/i]se adaptan a los cambios.[/td][/tr][tr][td]7.[/td][td][img width=24,height=24]https://lh5.googleusercontent.com/EeYLvel9HmsnYD7ZRVm-HBQtblHhlB35cdQzXdG11nyuG3R7BCgnyC_l3L8aKn1R4wNkQnlMJHA72jcGN8n5f2RRahLZMiuy01yMfDJFEssc0gxkkfajbgHSyt1KTilGP0RyH5NA[/img][/td][td]Selecciona la gráfica de [i]f(x) [/i]y [i]g(x) [/i]y cambia el color de las gráficas usando la[i] Barra de estilo[/i] para realzar tu construcción.[/td][/tr][/table]
Inténtalo
Números complejos
Tarea
Determine un número complejo y cambie sus coordenadas a polares. [br][br]Explora la construcción y aprende cómo visualizar números complejos en un sistema coordenado polar con la [i][url=https://www.geogebra.org/suite]Suite Calculadora GeoGebra[/url][/i]. A continuación, inténtalo tú mismo siguiendo las instrucciones que se encuentran más abajo.
Explora la construcción
Instrucciones
[table][tr][td]1.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/1/18/Algebra_new.svg/32px-Algebra_new.svg.png[/img][/td][td]En la [i]Vista algebraica [/i]abre la [i]Ayuda de entrada[/i] y selecciona [i]Texto[/i]. [/td][/tr][tr][td]2.[/td][td][/td][td]Copia el siguiente texto en la [i]Barra de entrada [/i]y presiona [i]Enter[/i]:[/td][/tr][tr][td][/td][td][/td][td]Representa números complejos en el plano complejo en forma rectangular y polar (incluyendo números reales e imaginarios), y explica por qué representan el mismo número.[/td][/tr][tr][td]3.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_complexnumber.png[/icon][/td][td]Abre la [i]Vista herramientas [/i]y busca la herramienta [i]Número complejo[/i]. Selecciona esta herramienta y haz clic en cualquier lugar de la [i]Vista gráfica[/i] para crear un número complejo. [br][b]Nota:[/b] El número complejo será denominado automáticamente [i]z[sub]1[/sub][/i] y sus coordenadas serán mostradas en la [i]Vista algebraica[/i].[br][/td][/tr][tr][td]4.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Abre las opciones de configuración global y cambia el tamaño de la letra.[/td][/tr][tr][td]5.[/td][td][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/2/25/Stylingbar_caption.svg/16px-Stylingbar_caption.svg.png[/img][img width=16,height=16]https://wiki.geogebra.org/uploads/thumb/b/bd/Stylingbar_point.svg/16px-Stylingbar_point.svg.png[/img][/td][td]Selecciona el número complejo en la [i]Vista gráfica [/i]y cambia su configuración. En el menú etiqueta marca [i]Valor[/i]. Cambia el tamaño del punto también.[br][b]Nota:[/b] En la aplicación móvil abre el menú contextual presionando el botón [i]Más[/i]. Luego en [i]Estilo del rótulo[/i] selecciona [i]Valor[/i].[/td][/tr][tr][td]6.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/34/Algebra_hidden.svg/32px-Algebra_hidden.svg.png[/img][/td][td]Escribe [math]z_2=z_1[/math] en la [i]Barra de entrada, [/i]presiona [i]Enter [/i]y culta el nuevo número complejo seleccionando el botón [i]Visibilidad [/i]que se encuentra a su izquierda.[/td][/tr][tr][td]7.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img][/td][td]En la [i]Vista algebraica, [/i]abre el menú contextual presionando el botón [i]Más [/i]de [i]z[sub]2[/sub][/i] y selecciona la pestaña [i]Álgebra[/i]. Cambia las coordenadas a [i]Coordenadas [i]Polares[/i][/i] y cierra el cuadro de configuración. El número complejo [i]z[sub]2[/sub][/i] se mostrará ahora en coordenadas polares en la [i]Vista algebraica[/i].[br][b]Nota: [/b]En la aplicación móvil, ingresa [math]z_2=APolar(z_1)[/math] para mostrar las coordenadas polares en la [i]Vista Algebraica[/i].[/td][/tr][tr][td]8.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Mueve el punto [i]z[sub]1[/sub][/i] en la [i]Vista gráfica [/i]y explora cómo los valores cambian en la [i]Vista algebraica[/i].[/td][/tr][tr][td]9.[/td][td][img width=32,height=32]https://wiki.geogebra.org/uploads/thumb/3/30/Menu-options.svg/32px-Menu-options.svg.png[/img][/td][td]Abre la [i]Configuración [/i]y selecciona [i]Cuadrícula visible[/i]. Activa una cuadrícula [i]Polar[/i].[br][b]Nota:[i] [/i][/b]En la aplicación móvil selecciona [i]Cuadrícula visible [/i] y cambia el [i]Típo de cuadrícula[/i] a [i]Polar.[/i][br][/td][/tr][/table]
