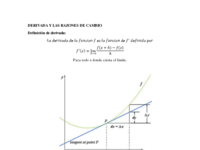
En la siguiente grafica al presionar el botón Inicio, se representa el recorrido de la función[br] V(t) = 1/6(60 - t )² la cual obedece al comportamiento de cómo se vacía un tanque cilíndrico lleno con 600 gl de agua.[br]El cual tarda 60min en vaciarse después de abrir el desagüe ubicado en la parte Inferior del tanque. Se supone la apertura del desagüe en el instante t = 0.

Después de revisar la gráfica, los trazos de las líneas y teniendo en cuenta El fenómeno de estudio, se plantean algunos interrogantes:[br][br]1. Realizar con lápiz y papel la gráfica de la función dada [br]2. En la gráfica obtenida identifique y subraye sobre la función dada el intervalo requerido en el ejercicio (t = 15 a t = 45). De la misma forma represente simbólicamente. (Simbología de desigualdades)[br]3. calcular la derivada de dicha función y representarla gráficamente en el plano.[br]4. represente simbólicamente el intervalo requerido en la gráfica obtenida de la [br]Derivada de la función.[br]5. Determine la razón instantánea con la el agua fluye fuera del tanque en t = 15 min.[br]6. Determine la razón instantánea con la el agua fluye fuera del tanque en t = 45 min.[br]7. Identifique la respuesta que determine la razón promedio con la que el agua fluye afuera del tanque durante la media hora de t =15 a t = 45.[br] a) 300/20 ; b) -10 ; 200/30 ; d) 10[br]8. de las siguientes respuestas identifique la razon de cambio de V en t=30[br] a) 10 ; b) -15 ; c) 15 ; d) -10[br]9. Que entiende por la derivada y las razones de cambio._____________________________________________________ _____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________[br]__________________________________________________________________________________________________________________