Sinus und Kosinus am Einheitskreis (Wel)

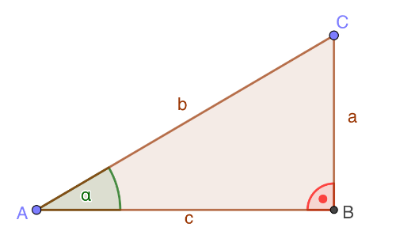
Definition von Sinus, Kosinus und Tangens als Seitenverhältnis im rechtwinkligen Dreieck.
Kreuze alle richtigen Antworten an.
Zur Erinnerung:
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAL0AAAAxCAYAAACPpaiTAAAKqUlEQVR4Xu2dR6uUSxPH+3wAszvFhQHcKcaNCrpQURHEHBBBMYJgzoiYM4gZBReKiroRzOBC3ZhAVwoGRFwa8QO8r7++9z+3Tp/nmZnnOXPOjDM9cDn3znRXd1f/q7qqurpu0//+fFz8RA40EAeaIugbaLfjUj0HIugjEBqOAxH0DbflccER9BEDDceBCPqG2/K44Aj6BsHAgQMH3IYNG1yXLl3c9+/fK77qtqZfyQlH0LeCm69fv3Z79+51V69e9VQA1KxZs9zJkydbQbXtum7ZssV9+PDBXblypU0GaWv6lZp0BH1OTgKc2bNnu/3797uFCxe6bt26OTb9x48fNQv68ePHuzFjxrj169fnXPU/3fr27esuXLjgRowY0YxOJein0W7VhIPOEfQ5uPnx40c3ZMgQt3HjxlYDKMfwubs0NTW5x48ftwBrFoIS9q9fv3pBt5/W0i9GO8scS7WNoC/FoYTfly9f7u7fv+/ev39fsndoAnEyhJoWe/js2bPe9Jg5c6br2rWrmzRpkpswYUKBvm3Tp08fP37v3r396bJnzx63efNmt3r1ajd37lx37949N27cOHf37t1Cf+YxcOBAJ7DKBl+2bFnhZPr27Zvbtm2bN384saD58uVLd+nSJQ9wNDm07UdCZOlrDqwlNKVu377ttm/f7l68eOHNwYsXL/p1FqPNeOXwseRm/Nsggr5cTv3bDmB0797dnT592i1ZsqRo7ydPnrjJkyd7u5+2Z86ccUuXLnU28wPQnjp1yt28edNrYIHYalIAwQdfoVOnTm748OFu8eLFrlevXv77z58/u4cPH3ohWLt2rXv79q2bOHFis3EY+9y5c+758+e+D77HoEGDmgng0KFD/W/4KNBiXNarPvyGwGsudvGiDw3m8OzZM2/+2bVKcGUaMYefP38WhDONdjl8zLKNEfRZuPWnLRswcuRI9+rVKzdgwADfW1qTf7eaHPt03bp1HvD0W7VqlQMUcnSlHa3JAa1r164VgIam3Lp1q3v69Kn79euXe/DggRccTgWAKSCi+WmDRlYfexIBME4Q5kIUB5rWJge0mzZtcu/evSuYLfThVNm9e3eBS6xp165dXmjsh/9Ge2sOoZBhEkILvvXs2dO3mzdvnueFaKXRLsXHjFsY0xCyMkwAD/P0ANSwYcMKWkvCIfqYG1OmTGl2OkjzheC0QLPHPt+PHTvW05DAQR9QoPllNiVpTOaHycIHf8Rqb75jHITIRp7oI/ODNhJSK3BaH211ovFdKDBWMWDWsI758+cXTLg02uXwMeseRk2fkWNJJkqSyZMmHHY4mS2yvbXBt27dKoAB5zDJDxAdq0ElCAjBsWPHWgCKE+XLly/e7AiBG46TtE6+O3jwYAtfRoC1px9CIJNNQsVf62dYXqTRLoePGbcwavqsDBPIBEQ5f9jlFkg4bNjVAgKAxixAkyaZJW/evHF37tzxTqmlgzmEhsdkYazz5897M0cmB9+j2XXhZE0m6OHcXr9+veBLWAHFP5BWRlA4AaAHABkD5xoz5MiRI348a3rRho98FUwjzUHCi19CX+bAX3wFa4Jh20sI0miXw8esexg1fVaO/WkvmxlwAkjAfPjw4RYmg5xSmRQ7duxoFpEBoFOnTvVgIfyJY4qtbc0dtWEsXX7t3LmzYHcL8IqSAGocXWjKNJHNrDY24hMKDxqaU6J///5eCDDZFL0BgNjhmElEfTSPkL5CutC6ceOGN8WYl6I68IPIDoKi0ymNNm1L8THrFtYU6NEQx48fb8aMUgtCQ3z69MlHDKRBS/Wphd8xbazWZ05oW8BgHcdamGu9zaFmQI8WQlty3IWXHqWYjrAsWLCgoFVKta/272EEyMbHiYD8TcJbbV7mGb+ioM/rdCgOa8NlWRcj4MtmzNq/vdsrPq+ISnjct/d8Gmm8mgA9R30YzsuzCTh906dP/6tSA/KsM/ZpHQcqCvo8U1E0JCn2m5VeWtgrK53Yvr45kBn0NndCUQkuOogyjB492nv2urghskAoj/Aen3379vm/9hZOSUZpRRlszoVyNTp27NjiVhS6NlSW5hfYS5JiWxuLRNQv8DOD3t68CeiKzybZ9Fx6ENaz+RZcmds+5I0kXVoo9EVIjPAYsWzCg3wGDx7cIsoh0Lc2k7B+tzuuDA7kAj1XyFyihFGGNNDbG0VdNkiT0icN9JwUAN8KhIQoyWFtD9AzfvzUDgfynMiZQY92J2FJ6asAOky8shMJr7cFTAt6m2Bl2Unfy5cvFxKSZP+nafJyQB/Nm9oBbLVmkhn0migAPHTokL+dLGXeWE0fgj7Npk8CMFEebivT8tjLsemrxeg4bu1wIBPolR6rC6QwKSmLeaN88bTojb4nb33atGn+cQOOLP4AORzkoIQ3l0lZi7XD6jiTWuFAJtBj2ixatMjnTfNR3gmOpo3e6MWMoje0JfGKjyI89JXGTntbqZwLOcIdOnTw/W0+iGVkjNPXCqxqex6ZQN9WS6nEjSwO8sqVKwtZfG0110j37+dATYAeNrYm90aZiMroq/a22AiPddgJAPAJ369We76NNn7NgB7G58myxK8A9LWUZamwbBhlwvzi8q5a+UEoFpvD3mhg13prCvT1sglpDjUXe9UqG0ImJ74TdyyNnrocQd8Gkga4whvjJO2vV0846nqzqrCr3rGGJT6IYpHakVTiw1ZbI5hw4sQJn6YdvjMNTayw9Ido24cfPGHs0aOHf/RCnpR9ObZixQofUbN3KknhY/v4hjmwRptKXskyH8W2NYK+wqDXc7wksraOpIA2Z84cn0dkTSFFs9JKfPz+/dvXsFGfMF2DsXk9ZR+kpIWGmUe/fv38Syie9fGGVrR5bjhjxgx/GcntO/PX0z/q4QBYhFJtbPW0sKoDc7KXjfLDFMGrdJmPCPoKA7sYOWn0sAIYQO7cuXNiHcmwmgG2v9WAAIv7CfudrSZGyBjtayschI/Ok8qCsA773BAg4iOFhazs+1n14a+tnBCW70g67TDvJFxhQmCly3xE0Lcj6AXQsMRGmFJhp2TfmOodq60rgxCsWbOmkI4RVh+Adlh8KhQk1b0Ji8vaSBPmBjY/2lygTEr9CAEeVk/TaWerOrBe3fMgoLa0SFuU+Yigb0fQJ71z1aamvRlQYSQ0OTa7BaYAlFTcCdMgqWBUUkEqtKxN6Va0LDStQlaF1RYkBPYkCws7JVVps3R1kx+WGMyTPJZna6NNn4drKX0EtrBODVoWRy+p6KkFH0d/GHpVbpJKiQgw1gewUSHZxmHJcDQ6mpcqB5g0CFhYr0f5VKNGjSqcKmG1BQtYlQahDScb/6h8CH6ASoBQ1ZkTxJb/oPaO+NEWZT6ipq8gsIsy06QdSzPbrM5il1Jp5o9AR+oHNDFBjh492qwkX1iSxFY703xVKY1IkS0EJU3O/QG/hX2trS0BpT4nbamNSYatyncklQ/hdMHxDtNX7BygW+kyHxH07QT6vMMAvEePHiXWtQ+rleUdI/b7jwPRvKkyGnSjnPR/Lyn1fqDKU/9rh4+gr9LWqQRIsRta2fO2hnyVpltXw0bQ19V2xsWUw4EI+nK4FNvUFQci6OtqO+NiyuFABH05XIpt6ooDEfR1tZ1xMeVwIIK+HC7FNnXFgf8DLLm+5vR7xYYAAAAASUVORK5CYII=[/img] und [math]cos\left(\alpha\right)\frac{ }{ }[/math] = [math]\frac{Ankathete}{Hypotenuse}[/math][br][br]Bei der Definition im rechtwinkligen Dreieck ist α beschränkt auf Werte zwischen 0° und 90°. [br]Um auch andere Winkelwerte verwenden zu können, ist man auf Betrachtungen am Einheitskreis übergegangen.
Was ist ein Einheitskreis?
Sinus und Kosinus am Einheitskreis
Man betrachtet nun einen Einheitskreis, dessen Mittelpunkt der Koordinatenursprung ist.[br]Zugleich ist der Mittelpunkt der Scheitelpunkt des Winkels [math]\alpha[/math]. Der erste Schenkel ist die positive (!) x-Achse.[br]Der zweite Schenkel von [math]\alpha[/math] schneidet dann den Einheitskreis in einem Punkt A.[br]Die x-Koordinate von A entspricht dann dem Kosinuswert und die y-Koordinate von A dem Sinuswert des Winkels [math]\alpha[/math].[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAukAAAHXCAYAAAABXMRLAAAgAElEQVR4XuydB3gVRdfHDyLw0nsRPinSBSHSO74IUgQEJBRBqoUiIDX0JlVFOqEohCKESEeavIL0qnQpCtIREQUEQhO+nMGNy+W2vXd37+zuf54nzyW5U878ziT8d+6ZMwkexRVCAQEQAAEQAAEQAAEQAAEQkIZAAoh0aXwBQ0AABEAABEAABEAABEBAEIBIx0IAARAAARAAARAAARAAAckIQKRL5hCYAwIgAAIgAAIgAAIgAAJPiPT/+7//AxEQAAEQAAEQAAEQAAEQAAETCJw/f97jKE+JdG+VTbAVQ4AACIAACIAACIAACICA7Qnw5jhEuu3djAmCgDMJ7Ny5kxYuXEiNGzemMmXKOBMCZg0CIAACIGBJAhDplnQbjAYBEPBFgAV63759qWjRonTgwAEaMWIEhLovaHgfBEAABEBAGgIQ6dK4AoaAAAjoRUAR6CzM+/TpQyNHjhSCHUJdL8LoBwRAAARAwGgCEOlGE0b/IAACphJQC3QOcfnvf/9LGzduJNefm2oUBgMBEAABEAABjQQg0jUCQ3UQAAG5CcyePZvy588fH9qiiHS2moX68ePHqWXLlnJPAtaBAAiAAAg4ngBEuuOXAACAgL0JqEW6vWeK2YEACIAACNiJAES6nbyJuYAACDxFACIdiwIEQAAEQMCKBCDSreg12AwCIOA3AYh0v1GhIgiAAAiAgEQEINIlcgZMAQEQ0J8ARLr+TNEjCIAACICA8QQg0o1njBFAAARCSAAiPYTwMTQIgAAIgEDABCDSA0aHhiAAAlYgAJFuBS/BRhAAARCwH4Fz587R888/H/DEINIDRoeGIAACViAAkW4FL8FGEAABELAWARbgJ06coNjYWGF40qRJKV++fPGinN9buXIlde/ePeCJQaQHjA4NQQAErEAAIt0KXoKNIAACIGANAjt27BDi++rVq24NTp8+PZUrV46+/fZbYpENkW4Nv8JKEACBEBCASA8BdAwJAiAAAjYjcPv2bfrss8+Id9C5cBgL75wnS5ZMfM/v8+658r4y/WnTpgVMAjvpAaNDQxAAASsQgEi3gpdgIwiAAAjIS0At0FmcN2rUSAh018ICfdiwYU/8GCJdXr/CMhAAgRATgEgPsQMwPAiAAAhYnAALbxbgZcuWpVatWrmdDQv5fv36iR11dRk7dmz8brtWDNhJ10oM9UEABCxFACLdUu6CsSAAAiAgFQGOQY+KihLhLf379/doG9dzF6fOwp7j1AMpEOmBUEMbEAAByxCASLeMq2AoCIAACEhHoG/fvkJ88wFQdyEuRhoMkW4kXfQNAiAQcgIQ6SF3AQwAARAAAUsSUGLMfe2iGzU5iHSjyKJfEAABKQhApEvhBhgBAiAAApYj8PXXX4t0i3Xq1KHatWubbj9EuunIMSAIgICZBCDSzaSNsUAABEDAPgT0EOm8G3/gwAERKqM1XAYi3T5rCTMBARBwQwAiHcsCBEAABEAgEAKc95y/ihYtGn+TqNZ+ghH6EOlaaaM+CICApQhApFvKXTAWBEAABGxFACLdVu7EZEAABPQkAJGuJ030BQIgAAIgoIWAkmOd0zfyAVQtBTvpWmihLgiAgOUIQKRbzmUwGARAAARsQYBDZcaMGSPypI8YMULznCDSNSNDAxAAASsRgEi3krdgKwiAAAjIR4DzpPNlRa4ladKk9Oqrr7o1mG8e/eyzz8RNpXxLKV9qpLVApGslhvogAAKWIgCRbil3wVgQAAEQkI4AC+6uXbs+YVeyZMlo+PDhxK+uhevHxMQIYR9MjnWIdOmWAgwCARDQkwBEup400RcIgAAIOJPA+++//8TEPcWYc4gLC3TeQWeB3q1bN7dC3h+KEOn+UEIdEAAByxKASLes62A4CIAACEhDwFWkswDnvOfKTjrvnrNAZ3HOhd9r3759wAKd+4BIl8b9MAQEQMAIAhDpRlBFnyAAAiDgLAJ8APT8+fMiBn379u3EceruCh8S5RtKA4lBd+0PIt1ZawyzBQHHEYBId5zLMWEQAAEQ0J0Ai3QW38qtobxjzjvnsbGxYiw+RMrvaU2z6M1QiHTd3YgOQQAEZCIAkS6TN2ALCIAACFiTgBJjbqb1EOlm0sZYIAACphOASDcdOQYEARAAARDQgQBEug4Q0QUIgIC8BCDS5fUNLAMBEAABEPBMACIdqwMEQMDWBCDSbe1eTA4EQAAEbEsAIt22rsXEQAAEmABEOtYBCICAK4EECRK4hTJ69Gjq1atX/HvR0dHUtGnT+O85pd6UKVO8Au3QoQNFRkZ6rJM7d276+eef49+vUaMGrVu3Lv571/f5jY8//pgiIiJEHXfvw8P2JACRbk+/YlYgAAL/EIBIx1IAARBQE9i6dStVrFjRp0hXC2N15erVq9PatWs9QtUi0vPkyUMnT55029ejR4/Ez5UHBa73wgsvELfhL282wOP2IACRbg8/YhYgAAIeCECkY2mAAAioCSji29eOtLLbruyuq3fVt2zZQhUqVPAbrLrtggULqEmTJqR+WFDGcPczFv3ffPNN/O67Yr8i4v02AhUtRwAi3XIug8EgAAJaCECka6GFuiBgDgHX3WwljETZWfYkgk+dOiXCPbwVX+JbCS/xFrqiFtXKDjaPqdjnGhbji5oi+NVjehrD08MBdtJ9Ubbf+xDp9vMpZgQCIKAiAJGO5QACchFwjfNWrGNxrYR+eNol1kOkewoxUY+pDnVR/1wR+L5CXtTE1eEv6r7Uc3G3u678jPtCTLpca9gsayDSzSKNcUAABEJCACI9JNgxKAh4JKAWyYpoVQtZbwI4WJHuq72yW63Y4+mQp78i3Z0QV4Px9MCidacey82eBCDS7elXzAoEQOAfAhDpWAogIA8BdZiLeqdYLWaNFKju4srVYyvhKL5Euq+QGoW4p1105X1Ph1iNZCDPaoAlvghApPsihPdBAAQsTQAi3dLug/E2I6AWpa5x58oOu1q8mzV9V1HuS6T7u5PuGl+uno+WcBezOGAcuQhApMvlD1gDAiCgMwGIdJ2BojsQCIJAsCLdV7gKm+bvLrd6Gq4x6HrEpHubK4/tKctMIHHvQbgETSUmAJEusXNgGgiAQPAEINKDZ4geQEAvAt5itJVdZ2876UaJdNedcz2yu3gS+gpLvXbr9fIN+pGPAES6fD6BRSAAAjoSgEjXESa6AgEdCKhv2HR3cNRbasRgRbpaOCuHRD3Fw/uTJ91bLL2vHXFfudP9ud1UB3egC4kJQKRL7ByYBgIgEDwBiPTgGaIHENCTgC+hHUi4ihb7FPHt2sZ1XE83jqrFszeRrsTYexPb/tw4qmVuqGsvAhDp9vInZgMCIOBCACIdSwIE5CPgKtSVg5iKaFVfIGSE9a7i2NNBUNcUia6C25tI93ZoVD0ndQYY/rnRDylG8ESfxhCASDeGK3oFARAwkEBkZCT9+OOPNHHiRJ+jQKT7RIQKIAACIAACEhKASJfQKTAJBEDAMwEW6DExMVS4cGGIdCwUEAABEAAB2xKASLetazExELAfgU6dOolJZcyYka5cuQKRbj8XY0YgAAIgAAL/EIBIx1IAARCwHIGhQ4c+JdLv379Pd+/epXv37j3x2rx5c+KUbokTJ6YkSZI88ZowYULLzR0GgwAIgAAIOIMARLoz/IxZgoClCPz222/0yy+/0Pnz5+nq1av0+++/i1fla//+/XTz5k165pln6Pbt20KYs+BmIc5fDx8+FEKdD27xV5YsWUQdVwHP7bl+qlSpKH369JQhQwbxqnwp3/Nrzpw5xVeKFCksxRLGggAIgAAIWJMARLo1/QarQcDSBDg38uHDh+mnn36i06dPiy8W5cq///Of/whBnD179qcEMwvoFStW0J07d2j8+PGULFkyIbRZcLsr3g6OPnjwQAj369evP/UwoH4w4IcGxTYW9Ipg59dcuXKJ7wsUKEA5cuSwtF9gPAiAAAiAgDwEINLl8QUsAQFbEuDd8EOHDglRzq/KV/78+SlfvnxPCF5F/KZOndorC3fhLp4a6J3d5dKlS089VLCA52wzsbGx9NJLL8V/8eFW/j5lypS29C0mBQIgAAIgYBwBiHTj2KJnEHAcAd6R3rFjh/javn07HThwQIShsFBVBKsiYjk+PNASSpHuzWbecVc/iCgPJtmyZaPixYtT2bJlqVy5clSyZMlAp452IAACIAACDiEAke4QR2OaIGAEAb7IQy3Kjx49KoSoIkaLFStGzz33nO5DyyrSPU302LFjtHv37viHF76oRc2J/+3r0wPdIaJDEAABEAABqQlApEvtHhgHAnIRuHHjBn3zzTfia/369cQZVdRis0yZMnIZHGeN3uEuekzwjz/+eOLhhj91CAsLo9dee018VahQQY9h0AcIgAAIgICFCUCkW9h5MB0EzCDwww8/xAvzLVu2ULVq1eLF5IsvvmiGCUGNIaNIdzehDRs2iAcffgA6c+aMYKyw5nAZFBAAARAAAWcRgEh3lr8xWxDwiwALxoULF9KaNWsoefLkTwhGzqRipWIVka5meu7cuSc+scidOze98cYb1KRJE8qTJ4+V8MNWEAABEACBAAlApAcIDs1AwG4EODtJdHS0+OJc4CwIWRhyFhYrFyuKdFfemzZtokWLFgnfFC1aVPimcePGyBpj5YUJ20EABEDABwGIdCwREHAwAY6NVoQ5H2ZUxF+pUqVsQ8UOIl3tjMWLFwufLVmyRPiLv+rUqWMbf2EiIAACIAACjwlApGMlgIADCThJ6NlNpCvLlW9f5ZAkFuzKAxYLdqR3dOAvNKYMAiBgSwIQ6bZ0KyYFAk8T2LZtW/yueZEiReJ3Ye1+0Y5dRbraw+pQJfYnh8KwYOcbW1FAAARAAASsSQAi3Zp+g9Ug4BeBn3/+WQhz3nF99OhRvDB30uFDJ4h09WJQDv2y38uXLx/vc6sd+PVrgaMSCIAACNiYAES6jZ2LqTmXwK5du2jChAm0bt26eJHm1NzbThPpyqrnhzLlvMHmzZupS5cu1LlzZ0qXLp1zfzEwcxAAARCwEAGIdAs5C6aCgC8CnAVk/PjxtGfPHiHK+CtRokS+mtn6faeKdLVTORyG18WcOXOEUOd1kTVrVlv7HZMDARAAAasTgEi3ugdhPwjEEeAdcxZhHN7CAqxjx47g8g8BiPR/l8Ivv/wi1gl/KWL9hRdewFoBARAAARCQkABEuoROgUkg4C+BZcuWibCW33//XYjztm3b+tvUMfUg0p929aVLl+LFeosWLYRgL1SokGPWBCYKAiAAAlYgAJFuBS/BRhBwIcCxxrwb+vDhQyGwmjVrBkYeCECke14af/75p1hH/KBXu3Zt8aBXvHhxqdbS6NFEt24RlS1LVLOmVKbBGIMJjCxNdHo3UZq4yKzRFwwezKDu14wgWtbv387D6hG1X+p9sMj6RPuXea6j8PC3ntLT+wnc9/lK3AevTScZBADdBkUAIj0ofGgMAuYSiIqKEqIqVapUQlA1aNDAXAMsOBpEum+n3blzJ35nnQ8Y89rizDChLjt2EK1ZQ5Qp02NLPvgg1BZhfDMJWF2kL4hbr99NfppYzri74vrs8kzSX/Htbz0eadc8oplvQ6SbuX71GAsiXQ+K6AMEDCYQGRkpdjtz5Mghds5r1apl8Ij26R4iXZsvlZ11Dn/htVa1alVtHehYO+6ZlG7eJMqdm4gFe1xkDuXJo+MA6AoEDCSg7FwrO9XqXfU2c4lKN/d/cHXbesPjPlXq676tp3rKA4OVP5Xwn5Z9akKk28eXmIkNCfDV7/3796d8+fKJ3U0WnCjaCECka+Ol1J4+fbrYXWexPmzYMLEGzS4DBxIVLkzUqBGR+t9m24Hx9Ceg7JKre47YTvRCXFiTUtztpKt/9v6iuDCYcv/Wd7dD7bqDrISbRGQjunaRyJNYPhX3UKju2x0Bb4JXLZbV81LG1Rpiogh+X+Eynuop3Hy119/T6DEYAhDpwdBDWxAwiABf896vXz/i1HkskOrWrWvQSPbvFiI9OB+PGDFCPCgOHTpUvJpVOMxFvXvOu+qXLxNFRJhlAcYxioAiVN31rxbN3kS6J9vUItQ1Hlxpw+KaBTqXaY/c9xSsSFeHuqjHUObkK+RFbZU6rMWTvVzfWz1PzL31Z5T/0a//BCDS/WeFmiBgCoGRI0cKMTR48GAaMGCAKWPaeRCI9OC9y6k9+aHx2LFj4qGxTp06wXfqo4dJ/xxkU+LQlfh0PjzKh0hRrElALX7VYRuKiFSLbF8iXb0brbRX726rhakiRtVC1ptQDlakK+O47rZrFemeeLl631s9X3Nx/QTDmivLnlZDpNvTr5iVBQmsXr1aiPPccQG4LITy589vwVnIZzJEun4+Wbx4sVijJUuWFGs0e/bs+nWu6inumSDu4qWnM7pwppfMmYlatTJkWHRqAgFXwehNIPoS6epdYNeda3WYi/phQD2+1pATLXh8iXR/Y8P12EV3Fwuv5oAQGC2eNbcuRLq5vDEaCDxF4MKFC0L4bNu2TQifRhyAi6IbAYh03VDGdzQwLkD8448/Fuu1R48eug8QE0N0+LDnbuMib1AsTMBdVhJ3u9q+YtLVaRm9iXTXuHNlh93bAcxg8foS6f6Gu7gePvVkl7/11O092Rjs3NFePwIQ6fqxRE8goJnA2LFjhUD/8MMPafjwuCP7KLoTgEjXHano8HCciuYQmF9//VWI9WrVquk2kKcdcyXkBTnTdUMd0o7cxUmrd7dDKdJ9hYgwOG+74XrEpKs/DfCWDcbfeq7O9mRjSBcFBn+CAEQ6FgQIhIDAhg0bhDhPly6dEOdFixYNgRXOGBIi3Vg/f/nll2Its0hnsZ5JSWoe4LC+Ys9ZwCdPjpzpAeKVtpm7sI5gRLq3GG1l19nbTnqwIl2P7C7+imh/67k6Hzvp0v46xBsGkS6/j2ChjQhcvXpVCJpVq1YJQcNXsqMYSwAi3Vi+3Pu9e/fEuua0jfzQ2bFj3BWGARbO4nLqFMVlk3HfgRIKg5zpAQIOcTNPucLVQlOJUw9GpPM01Wke3R0c9RaLHaxI5/H9yZPuLUbe30Omvuq5Y2tWbH6Il5vlh4dIt7wLMQGrEJg9ezZ169Yt7tBbKyHQkyZNahXTLW0nRLp57tu7d68IgeEbTCdPnhyX4zwuybnGwvnQX3jB8+FQ5VCptzoah0R1kwm4y5GumOBvdhfXUBN3u8m+hLa/hzcDxePpxlH1HL2JZXcZb9zZ4k895YHBtb3RDAJlh3aPCUCkYyWAgAkEOnXqRJs2baKpU6dSuXKq2zdMGNvpQ0Ckm78CJk6cKA6UTps2TTyUooCAKwF3AtY120qwO+k8pqtQVw5sKsLW6PSDrrnaXXfvvYl0fw+D+lvP9QyAv4dXsXpDRwAiPXTsMbIDCBw8eJDatWsn0imyYEmcOLEDZi3XFCHSQ+OPHXHB5e+//z5VrlyZWLSjgAAIgAAIaCMAka6NF2qDgN8EZs2aJUTKZ599Rh8oN7L43RoV9SIAka4XSe39cKw6P6QePXpUPKQWKVJEeydoAQIgAAIOJQCR7lDHY9rGEuCDc1u3bhXCpEyZMsYOht69EoBID/0C4fh0TjPKvw9t2rQJvUGwAARAAAQsQAAi3QJOgonWIbB//36xc1ioUCERf54oUSLrGG9TSyHS5XDszp07xe9G+fLlxaFSFBAAARAAAe8EINKxQkBAJwJffPGFCG+ZMGECdejQQade0U2wBCDSgyWoX/sHDx6I3xG+CIl31cPCwojDwvbs+YFy5Pg/atCgAeXNm1e/AdETCIAACFiYAES6hZ0H0+Uh0L59e+KdQt49L126tDyGwRKCSJdvEURGRhJnPMqX7yVKkCAz5cxZnf744zx9//0k+uqrGHrjjTfkMxoWgQAIgIDJBCDSTQaO4exFYN++fWJnkA/E8c5gwoQJ7TVBG8wGIl1OJ/KnTevXn6SmTdfFG3jixEratq0LnTsXd5sRCgiAAAg4nABEusMXAKYfOIEZM2YIgc7xtbyTjiInAYh0Of1SrVptSpu2LRUoUP8JAz//vABt3742bnc9p5yGwyoQAAEQMIkARLpJoDGMvQj06dOH1q1bJ3bPS5Ysaa/J2Ww2EOlyOjQ8vAk9eFCbXnqp+RMGTpqUlfbt2xEXo55DTsNhFQiAAAiYRAAi3STQGMY+BHj3/NSpU7Ro0SJKnTq1fSZm05lApMvp2Dlz5lDfvmOoSZNvKVmyDMLIpUub0b17R+j48f1yGg2rQAAEQMBEAhDpJsLGUNYn0KhRIzGJmJgY60/GITOASJfT0cePH6eXX36Znk2QnHJmrUx/XT9HidLcoRs3LlPv3r1FXnUUEAABEHAyAYh0J3sfc/ebwLVr1yg8PJxy584tMrigWIcARLp8vvr7779FvvQmTZpQsWPFaMu0LZQpUSZ69967dOLECfG7xhlehg4dKp/xsAgEQAAETCIAkW4SaAxjXQK//PKLEA3VqlWjkSNHWnciDrUcIl0+xzdv3pzSpElDkyZNoov9LtKlEZcoQeIEVOxuMWHslStXxO/cSy+9RBMnTpRvArAIBEAABEwgAJFuAmQMYV0CP/zwAzVs2FDclNirVy/rTsTBlkOky+X8IUOG0I4dO2jt2rXCMHcinX/Ou+38u5c8eXKaN2+eXJOANSAAAiBgAgGIdBMgYwhrEvj222+FSPj444/p3XffteYkYDUuM5JoDXz55Zc0aNCguFzo2yhz5sxeRbpidps2bejy5ctxlxx9FXfANJlEs4EpIAACIGAsAYh0Y/mid4sSYEHAh0Q5g8ubb75p0VnAbCaAnXQ51sGuXbtEHPqmTZvEq1I87aSrre7evbvYfeffy2zZsskxIVgBAiAAAgYTgEg3GDC6tx6B6dOni+wSLNCrVKlivQnA4icIQKSHfkFcvXpVCHP+vWrVqtUTBvkj0rnB8OHDae7cuUKoc6w6CgiAAAjYnQBEut09jPlpIjB69Gjim0RZCHB6OBTrE4BID70Pa9euTWFhYTRs2LCnjPFXpHPDKVOmEMe08+9npUqVQj8xWAACIAACBhKASDcQLrq2FgHe5eM4dBYAuJLcWr7zZi1Eemh92bVrV7p06RJFR0e7NUSLSOcOFixYQC1bthS/p5ymEQUEQAAE7EoAIt2unsW8NBEYOHAgbd68mZYvX45bRDWRk78yRHrofDR58mSaNWuWOCiaJEkSXUQ6d8KZYWrVqkXr16+nV199NXQTxMggAAIgYCABiHQD4aJraxAYO3YsRUVFiV30DBkeX0+OYh8CEOmh8eW6deuocePGQqAXKlTIoxFad9KVjhYvXiyyLv3vf/+jYsUe51dHAQErEJjzCdEEVUbfVxsSjf7KP8uP7CZqWfrJunsfPd12TNyFvQvG//vzpl2Iuo97ul5EONG3i/79eab/I1p9zj9bUMt4AhDpxjPGCBITYHHOu+gs0PPmzSuxpTAtUAIQ6YGSC7zdyZMnxUFRvp23Xr16XjsKVKRzp59//rm4YIyFeq5cuQI3GC1BwCQCruJZGfalMkSzdng34pu4iLG+Td3Xmb2LqFCpx++5Cm+lhevDQK3niX4777s/k9BgGDcEINKxLBxLYMWKFdSsWTMh0EuV+uevm2Np2HfiEOnm+7ZixYoiXrxHjx4+Bw9GpHPnn3zyCS1cuFAIdb7FFAUEZCZQIsFj65SdbfWu+ogFRK818Wy9IqoVsa3eVVf6U/9Mqad+MFDEvLtx3bWVmaUTbINId4KXMcenCGzZskXEsq5cuZKqV68OQjYmAJFurnNbt24t4s95F92fEqxI5zH69u1Le/bsETHqKNYhoAhWxWJ/QzI87Tq3Lkt0aOeT81fvMCvvuO5IK2JWEcGexLK7UBNX2t7CRdTCWG2XMq6n+fMYapvdzUmxw534VrdV5qbstrvaqzD0Z2ffOivNupZCpFvXd7A8QAKHDx8WAn3cuHHUtKmHzw4D7BvN5CMAkW6eTziX+caNG8Wutr9FD5HOY7Vr147++OMPiomJ8Xdo1AsRAW9hG64hGa5CXm2yO6Hrbkpq0e0aD67UZ7GqhH64i/HmesGKdPWOtnoMf4Sxui2LeSXe3J8YcnX4i6e5KRyUBwaI9BD9crgMC5Euhx9ghUkELly4IAR6586dqUOHDiaNimFCSQAi3Rz6HHISEREhDopquRVUL5HOs+SDqhzyMm3aNHMmjVECIqCIUrXAVO+CK+JbLS7VQlsR7kp7tXju/DFRi56PzXIND1H/jP+tCFb1ON7EabAiPZjda09x5ooD3IlvV3u97cBzP+oHGG+7+gE5HY0CIgCRHhA2NLIigdu3bwuBzher9OvXz4pTgM0BEIBIDwCaxibff/+9OCjKqRFfeeUVTa31FOk88GuvvUbFixcXB0pR5CPgSVAru+uKkHQXb63MxjWkI9sLT2Y88SRG1Tv4ajHvbSw9CfoS6d52xdUiXfm0QT0fd6LaVaR7yyKjZurP7ryeXNCXZwIQ6VgdjiHw+uuvU8GCBenTTz91zJwxUSKIdGNXwfXr16lChQrUpUsXeueddzQPprdIZ3uqVq1K4eHh1KuXKs+dZsvQwAgC7uKj3Y3jrZ47oe9up9l1V9xbn8quu1q86z1/XyLd2y6+p08V/AmV8fUQ4hoC5GvHXW8u6A8iHWvA4QSaN29OiRMnppkzZzqchPOmD5FurM/r169P+fPnp1GjRgU0kN4inY04ffq0EOocfsO51FHkIWCUSFdm6C6toLLLHKxIDzbcRa+YdLWI9kekMxtP9SDQ5fndcGcJdtLl9g+s04FAp06d6Pz587R06VIdekMXViMAkW6cx3r27Em//PILLVqkug1F43BGiHQ2Yd++fSK8bfr06dSwYdxtMShSEPAU7qL8XIk99zfcxduur+uBSU9jMxglzt3bTnqwIj2Y7C6eUjW6im9Ph0TdiXQIdDEVK8kAACAASURBVCl+JbwaAZEuv49gYRAE+KKizZs3i1zoCRMmDKInNLUqAYh0YzzHhzMjIyPFQdHkyZMHPIhRIp0N2rBhgxDq/PtfpUqVgG1EQ30JqA+Juju8qQhldT134l0JD/EkYN3lB/c1tre47WBFuvphwFuedE8PKMqDhDJvd/XcHf50F7uu9VCpvisAvflLACLdX1KoZzkCvLvHO32cPzlDhgyWsx8G60MAIl0fjupeWPTyZUVbt26lsLCwoAYwUqSzYZySkfOo8+HW1KlTB2UrGutDwJvYdT206G8KRnc50hVr1cLbl9A2+tCkpxtHPdmoPhDqLX3k6nP/+sYTC/XcfGWLMZqDPivJ/r1ApNvfx46cIcekcoaHBQsWiGwPKM4lAJGur+/PnDkjDoqOHTtWlzASo0U6z54PkJ49e5aio+PuVUeRhoCrAPe0i+0qKD0dsHQngP3JeqL0p8SzG31w0lVsu87bW6iPa455TyxcmbmO4S52X70wINLl+DWBSJfDD7BCZwJ8i2jlypXFDhqKswlApOvrf+bJv1+9e/fWpWMzRDobymEvNWvWpB49euhiNzoBARAAAaMJQKQbTRj9m06Ahfnx48dp8eLFpo+NAeUjAJGun084U8qjR4/o888/161Ts0T6Tz/9RCVKlKBly5aJtJwoIAACICA7AYh02T0E+zQRWLJkCXXr1o327t2LOHRN5OxbGSJdH9+OHj2a1qxZQ999950+Hf7Ti1kinYfjcBc+TM7x6SlTptR1HugMBEAABPQmAJGuN1H0FzICHCvLO2Vz586lGjVqhMwODCwXAYj04P3Bn0rxZUV8UDRnzpzBd6jqwUyRzsNyuMvFixdp/vz5us4DnYEACICA3gQg0vUmiv5CRoDjTflq8v79+4fMBgwsHwGI9OB8cuDAAXFQlO8Z4AuC9C5mi3S2n9dE7dq1qXv37npPB/2BAAiAgG4EINJ1Q4mOQkmAhfmRI0dwYVEonSDp2BDpgTvm1q1bQqC///771K5du8A78tIyFCL9xIkTIvvT119/LQ6Yo4AACICAjAQg0mX0CmzSRIAPgnXu3FnEoWfKlElTW1S2PwGI9MB9HB4eTjly5KBPP/008E58tAyFSGeTONxl6NCh4u9GihQpDJsfOgYBEACBQAlApAdKDu2kIHDu3DkRhz5r1iyqVauWFDbBCLkIQKQH5o8+ffrQ0aNHRTYUI0uoRDrPicNdLl++TPPmzTNyiugbBEAABAIiAJEeEDY0koXA66+/TmXKlKEBAwbIYhLskIwARLp2h3zxxRfisiI+KJomTRrtHWhoEUqRzmZyuEu9evWoa9euGqxGVRAAARAwngBEuvGMMYJBBDiVGh9qW758uUEjoFs7EIBI1+bFTZs2icuKWKDzp1RGl1CL9GPHjon49LVr11LFihWNni76BwEQAAG/CUCk+40KFWUiwAe++CAbx5NmyZJFJtNgi2QEINL9d8iFCxfEQdGRI0dSkyZN/G8YRM1Qi3Q2ncNdRowYQYcOHaKECRMGMRs0BQEQAAH9CECk68cSPZlIICwsTKRabNiwoYmjYigrEoBI999r1apVE+EfZqYxlUGkM6G2bduKg+f8gIICAiAAAjIQgEiXwQuwQROB4cOHizCXmJgYTe1Q2ZkEINL983v79u0pNjaWoqKi/GugUy1ZRPqlS5cof/784kbVYsWK6TQ7dAMCIAACgROASA+cHVqGgADnN+b/SPk1b968IbAAQ1qNAES6b4+NGTNG3DHAcehmF1lEOs97woQJIjZ99erVZmPAeCAAAiDwFAGIdCwKSxFo1KgRFS1alPr162cpu2Fs6AhApHtnzwev+bIiFuh58uQx3VEyiXSePMfkc+hL69atTWeBAUEABEBATQAiHevBMgQWLVpEH330kQh1QQEBfwlApHsmxbf0sihdsGAB1ahRw1+kutaTTaRzdpu33npLfFqXPHlyXeeKzkAABEBACwGIdC20UDekBDjMhT+Wr127dkjtwODWImAlkc672ZwG8NGjR4ZDvnv3rhDoLVu2pA8++MDw8TwNIJtIZzs7duxIiRIlonHjxoWMCwYGARAAAYh0rAFLEODLis6cOUNz5syxhL0wUh4CVhHpp06doty5cwtwZoj0pk2bUubMmUMuRGUU6deuXaN8+fKJ21bLlSsnz2KGJSAAAo4iAJHuKHdbc7IHDx6k0qVLi4+fn3/+eWtOAlaHjIAVRHp0dDSxaFaK0SKdH3r37dtHfN9AqIuMIp2ZTJ8+XYQBbdy4MdSIMD4IgIBDCUCkO9TxVpp23bp1Re7m7t27W8ls2CoJAdlFuhLiMnr0aEEsIiLC0J302bNni1zgPG6GDBlC7iVZRTqD4bzxDRo0IE5PiQICIAACZhOASDebOMbTRGDu3Lk0efJk2rlzp6Z2qAwCCgHZRbraUx9//LGhIn3btm1UqVIl4tcyZcpIsUhkFum7du2imjVrik/xZHigkcJhMAIEQMA0AhDppqHGQFoJ8ME2jgv94osvqGrVqlqboz4ICAIQ6Y8XwuXLl8VB0UGDBlHz5s2lWR0yi3SGxJ/g3bp1i6ZOnSoNMxgCAiDgDAIQ6c7wsyVn2aNHD7px44aIDUUBgUAJQKQ/Jsc7wny2Y/DgwYGiNKSd7CL9zp07YrNg1qxZ9OqrrxrCAJ2CAAiAgDsCEOlYF1IS2L17N1WvXl18zJwxY0YpbYRR1iAAkU7UqVMn+vPPP2nevHnSOU12kc7AOKtUZGQk7dixQzp+MAgEQMC+BCDS7etbS8+ML1apU6eOyFeMAgLBEHC6SB8/frzIUsIHRZ999tlgUBrS1goinSfOf4944yCUOeUNcQA6BQEQkJYARLq0rnGuYZzyjLMpHDt2zLkQMHPdCDhZpK9atYpatGghDooWKFBAN6Z6dmQVkb5582Zq27Yt/fTTT3pOH32BAAiAgEcCEOlYHNIRqFevntixQtoz6VxjSYOcKtKPHz8uDopyLLXMt/RaRaTz4q9Vqxa9+eabQqyjgAAIgIDRBCDSjSaM/jUR4JhPvtTl9OnTmtqhMgh4IuBEkf73338Lgd64cWP68MMPpV4cVhLp69ato549exJfsIYCAiAAAkYTgEg3mjD610SABXrJkiWpW7dumtqhMgjYQaTr5cW3336bUqdOTZMmTdKrS8P6sZJIZwhVqlQRO+nNmjUzjAk6BgEQAAEmAJGOdSANgf3794swl4sXL1LChAmlsQuGWJuAlXbS9SA9ZMgQkYVk7dq1enRneB9WE+nLly+n4cOHE2egQgEBEAABIwlApBtJF31rItC6dWvKmzcv9e3bV1M7VAYBbwScJNK//PJLGjhwoDgomiVLFkssDKuJdIZatmxZEfbSoEEDSzCGkSAAAtYkAJFuTb/ZzmrO5MIXrfAuevLkyW03P0wodAScItL5CnuOQ+fsSPxqlWJFkR4dHS3ypm/atMkqmGEnCICABQlApFvQaXY0mTO58KVFQ4cOteP0MKcQEnCCSL969aoQ5hEREdSqVasQ0tY+tBVFOs/y5ZdfFmEvnPEFBQRAAASMIACRbgRV9KmJwJkzZ0SYy6VLlyh9+vSa2qIyCPgi4ASRzhftFC1alIYNG+YLh3TvW1WkR0VFEe+oWyX2XzrHwyAQAAGfBCDSfSJCBaMJcCYXPij6ySefGD0U+ncgAbuL9K5du4oHXBaMVixWFenMumDBgjRlyhTiNYYCAiAAAnoTgEjXmyj600Tg8uXLlDVrVuLddF6MKCCgNwE7i/TJkyfTzJkzxUHR//znP3qjM6W/YET6wawHKVmJZJRnRR5TbHUdhOPSOXf6smXLQjI+BgUBELA3AYh0e/tX+tlxJpe//vqLJk6cKL2tMNCaBOwq0lkcNmrUSAj0woULW9M5cVYHI9JlmHSuXLlo/vz5IuMLCgiAAAjoSQAiXU+a6EsTgRs3btBzzz1HBw4coDx5QrMTpslgVLYkATuK9JMnT4qDoryTW69ePUv6RTHa6iJ97NixxJl1rBpuZOnFA+NBwOYEINJt7mCZp/fRRx/R2bNnacaMGTKbCdssTsCOIr1ixYr0xhtvUI8ePSzuHe876VdnXaXTbU4/Mcfij4rHf68Od7k05BJdHHyRcs7M+UQb/j59638PpLv2ye/f3HmTfp/+O6n79hfsw4cPRcjemjVrRMYXFBAAARDQiwBEul4k0Y9mAjly5KCVK1dSkSJFNLdFAxDwl4DdRDpf+pUkSRKaOnWqvwikrudpJ/3m1pt0vOJxyjo4Kz036Dkxh6MljorXgnsLild3Ij3Rc4moyMXHf1N+rvszXV95PV58KwJd3ef3Cb4nbsNFaacVGKeO5TSY48eP19oU9UEABEDAIwGIdCyOkBDgXSfeSd++fXtIxsegziFgJ5HOebk3bNhA3377rW0c6EmkK4I6/5b8lKJCivj5snhXvve0k67snCtCX9lNZ9F+/+L9eJHPnSo78KnrpA74AOrx48epcuXK9Ouvv9rGL5gICIBA6AlApIfeB460oGXLllS8eHHq3LmzI+ePSZtHwC4ifeHChdSrVy9xUNROmZC8xaTzLjeXDO9loBzTcjy1aNyJdLWodxXpXJ/FuLovpY6nMfxdqVWqVKFOnTpR/fr1/W2CeiAAAiDglQBEOhaI6QRiY2MpTZo0dO7cOcqUKZPp42NAZxGwg0j//vvvxUFR/gTqlVdesZUDfR0c5RCX29/fjp+zOlTFX5GutPEm0tX9BgJ42rRptHHjRhwgDQQe2oAACLglAJGOhWE6gVmzZolY9CVLlpg+NgZ0HgGri/Tr168Lgd6lSxd65513bOdAXyJdPWFFsCvhK3qK9GB30tlPadOmFbHp/IoCAiAAAsESgEgPliDaayZQo0YN4sNvjRs31twWDUBAKwGri3QOn8iXLx+NHj1a69QtUV+LSHc9TKpVpBsVk66Abtq0qYhNb9eunSXYw0gQAAG5CUCky+0f21l3+vRpkabszz//tN3cMCE5CVhZpPfs2ZNOnTpFixcvlhOuDlZ5EunqlIrKQdAz758RqRKVuHOtIt1V5Cvfc3aXRFkTPXGgNJCpLV++nDhv+nfffRdIc7QBARAAgScIQKRjQZhKYNSoUXTmzBlxCQsKCJhBwKoinWOcp0yZIg6Kpkjxb3YTM5iZOYa3nXRFqKvtUR8M1SrSuR/XPOkci37v4r2A86S7suIL2jg2vUCBAmZixFggAAI2JACRbkOnyjylsLAwkUuYPxJGAQEzCFhRpHOKxbp16wqBzr8zdi5awl2swKFr166UOnVqGjx4sBXMhY0gAAISE4BIl9g5djNt586dIhb96NHHF5KggIAZBKwm0vmTJj4oymETDRs2NANRSMewm0jH37mQLicMDgK2IgCRbit3yj0Z3mHi1IuDBg2S21BYZysCVhPpbO9rr71Gffr0sZUfPE3GbiKd58nnbvghy27pMh2xIDFJEJCIAES6RM6wuymI1bS7h+Wcn5VE+rvvvksPHz6kL774Qk6YBlhlR5GOszcGLBR0CQIOJACR7kCnh2LKyHoQCuoYkwlYRaRzisXVq1fTpk2bHOU4O4p0ZLFy1BLGZEHAMAIQ6YahRcdqAsgfjPUQKgJWEOmcYrFz587ioGjOnDlDhSok49pRpDNI3AcRkuWEQUHAVgQg0m3lTjkng5v45PSLU6ySXaQfOHBAHBRdunQpVa1a1SluiZ+nXUV6VFQU8SeI7FcUEAABEAiEAER6INTQRhOBmTNn0jfffEPR0dGa2qEyCOhBQGaRfvv2bSpfvjy999571L59ez2ma7k+7CrSY2NjxUH5y5cvi1cUEAABENBKACJdKzHU10yAQ104WwWnX0QBAbMJyCzSw8PDKXv27DRmzBizsUgznl1FOgOuU6cOtWjRgtjPKCAAAiCglQBEulZiqK+ZQPr06Yk/0ufFhgICZhOQVaRzisUff/xRhEQ4udhZpE+YMIEOHTpEM2bMcLKLMXcQAIEACUCkBwgOzfwjsHnzZurWrRvt3bvXvwaoBQI6E5BRpHOKxc8++0wcFHV6KISdRfqxY8eoevXqxBdUoYAACICAVgIQ6VqJob4mAgMGDKC///6bRowYoakdKoOAXgRkE+mcYpHDv1iglyhRQq9pWrYfO4t0dkqBAgVowYIF4oIjFBAAARDQQgAiXQst1NVMoHTp0sT5n3HznmZ0aKATAZlE+sWLF8VBUX5o5bMaKER2F+mcWjNbtmwUEREBd4MACICAJgIQ6ZpwobIWApcuXaKCBQvStWvXtDRDXRDQlYBMIr1atWpUqVIl4k+YUB4TsLtIX7lyJY0bN46+/fZbuBwEQAAENBGASNeEC5W1EJg9ezatWrWKYmJitDRDXRDQlYAsIp1TLHLKRf69QPmXgN1F+t27dylZsmRisyJlypRwPQiAAAj4TQAi3W9UqKiVQMuWLUUTiBKt5FBfTwIyiHROsbhkyRIRh47yJAG7i3SeLd8+2qFDB6pbty7cDwIgAAJ+E4BI9xsVKmolkC9fPiFMChcurLUp6oOAbgRCLdI5xSJfVsQCPU+ePLrNyy4dOUGkDxkyhO7cuUMjR460i9swDxAAARMIQKSbANmJQ1y4cIHCwsLoypUrTpw+5iwRgVCKdM6DzgdF58+fTzVr1pSIijymOEGkr1+/noYNG0ac2QcFBEAABPwlAJHuLynU00Tgq6++onnz5jn+ohZN0FDZEAKhEun37t0TAp1vnOzUqZMhc7NDp04Q6Tdv3qR06dKJ3fRnnnnGDm7DHEAABEwgAJFuAmQnDsEXGGXKlIl69+7txOljzhIRCJVI5xSL/Dswfvx4iWjIZ4oTRDpTL1mypMjywg9uKCAAAiDgDwGIdH8ooY5mAmXLlqVRo0ZR5cqVNbdFAxDQk0AoRDqnWPzhhx9EdiMU7wScItI5X3r27NmpR48eWBIgAAIg4BcBiHS/MKGSFgL8kS6nHOPUY4kSJdLSFHVBQHcCZot0zmbElxXxQdEMGTLoPh+7degUkR4dHS3S0fJhehQQAAEQ8IcARLo/lFBHE4GNGzdS//79kW5OEzVUNoqAmSJ9+/btVLFiRbH2y5QpY9SUbNWvU0T6mTNnxJrgS95QQAAEQMAfAhDp/lBCHU0EOM3Y0qVLaffu3ZraoTIIGEHALJH+22+/iXjjgQMH0ttvv23EVGzZp1NEOjsvV65cxJlekIrTlksZkwIB3QlApOuOFB2+9dZb4vIOzmqBAgKhJmCWSOcUi6VKlSLOiY3iPwEniXS+zKh169ZUv359/wGhJgiAgGMJQKQ71vXGTbxIkSIUFRVFxYoVM24Q9AwCfhIwQ6RzisU//viDvvzySz+tQjWFgJNEer9+/ShJkiTi0xYUEAABEPBFACLdFyG8r4nAgwcPxGFRzhGNQ6Oa0KGyQQSMFumcYpEvK+I49GeffdagWdi3WyeJdD48unjxYuJ7JFBAAARAwBcBiHRfhPC+JgL79u0TYS6HDh3S1A6VQcAoAkaK9NWrV4v4cxboBQoUMGoKtu7XSSL9yJEj9Oabb9KxY8ds7VNMDgRAQB8CEOn6cEQv/xCYM2cOrV27VuwsooCADASMEuknTpwQB0VnzpxJderUkWGqlrTBSSKdHZQ4cWK6du2aSFOLAgIgAALeCECkY33oSqBnz57i+us+ffro2i86A4FACRgh0h8+fCgEeqNGjahr166BmoZ2cQScJtKLFy9OU6ZModKlS8P/IAACIOCVAEQ6FoiuBDjDRYcOHbCzqCtVdBYMASNEOoe4pEqViiZPnhyMaWjrQJHeqlUrqlChAr3zzjvwPwiAAAhApGMNmEeAn/q2bt1KOXPmNG9QjAQCXgjoLdI5xSJfWrRu3TpwD5DA7zd/p4vXLtKl65fo0cePKOOcjJQgcQIqdtf+GaHGjBlDZ8+eJT5wjAICIAAC3ghgJx3rQzcCsbGxlCZNGrp7965ufaIjEAiWgJ4inc9aDBgwQBwUzZIlS7CmOab9zbs36esDX9PXh+K+Dn5NCRMkpMypMlOW1Fmo4YaGVHp1XOhHIqLi94rbnsmyZcvEOYYVK1bYfq6YIAiAQHAEINKD44fWKgJHjx6levXq0fHjx8EFBKQhoJdI5xt0OQ59w4YNVLFiRWnmJ7MhX+76kubvmk9rDq+hagWrUdVCVenVAq/Sc6mfizf7r4/+or/G/OUYkb5//36RAevgwYMyuw62gQAISEAAIl0CJ9jFhDVr1tC4ceMQBmAXh9pkHnqIdL6oiAV6r169xI2RKN4JrD28lkasHkH3H96nVmVbUdUXq1KyxO6zmThNpHNml+zZs9ONGzewjEAABEDAKwGIdCwQ3QhERkbSgQMHaOrUqbr1iY5AIFgCeoh0TrHIN+kOHz48WHNs3X7P6T00YtUI+vHSj9SpSid6s/ibPufrNJHOQNKnTy9ypWfMmNEnH1QAARBwLgGIdOf6XveZR0REUNq0aal37966940OQSBQAsGKdE6xePHiRVq4cGGgJjii3cxtM6nd3HY0oPYAeqei/5lLnCjSOQ0jb2aULFnSEWsDkwQBEAiMAER6YNzQyg2Bxo0bU/369alJkybgAwLSEAhGpBd/qzgd2nBIZCwqlaeUNHOSzZB+y/rRV3u+ovFNx1PY82GazHOiSOdbR/nvZHh4uCZWqAwCIOAsAhDpzvK3obPlyzk4rViZMmUMHQedg4AWAoGK9KaDmlL0yGhK0TAFpX0+La3uvJoKZyusZWjb173/9316+4u36Y9bf9C4xuMobfK0mufsRJHeo0cPypw5M/HlbyggAAIg4IkARDrWhm4E+D8djklHajrdkKIjHQgEItJHx4ym3q16U9V3q1KP93pQ88+bU8r/pKTVXVZTgSwFdLDKHl28MekNypgyI31U76OAJ+REkT5p0iTibFi4DCvgZYOGIOAIAhDpjnCz8ZO8f/8+JUuWjPgVBQRkIqBVpG8+sZkqV65MeUrkoc3zNoup7Du7j5p93kwIUt5Rz5Mpj0xTDIktXWO60s+Xf6bpLaYHNb4TRfqSJUto3rx5xK8oIAACIICddKwBQwn8+uuvFBYWRvyKAgIyEdAi0vkGzHwV89EzCZ+hHat2PBG+sff0XrGjni9zPtrTf49uU+yzpA+NWjPqqf72D9xPRZ8vGv/zBO8miP93s9LNaN478zza4KlPpcGjGY/i2+aIyEFn/zgb/736Pf5h5U8qEz+4cFFsmrxxMk3fPJ2WdlxKSRMlDYqFE0X6pk2baODAgcSvKCAAAiAAkY41YCiBI0eOUKNGjYhfUUBAJgJaRHqe1/PQyf0n6eu1X1Ox7E9fUb/q0Cp6d/a7NOrNURRRI0KXabLw5+JNdLOQrpi3Ynwd1+/9MWTFgRXE4SmT3ppEHf/bUTRhAX7699N0ZvQZ8T3bwhcQKUKdxfj5P8/TyAYj6cC5A9Q5ujP1rtmbGk9rTMs/WK5L6I8TRfrhw4eJD9rj76U/Kxd1QMC5BBDu4lzf6zrzzZs3i+vSsTOkK1Z0pgMBf0V69c7V6ZtZ39DQz4fSOzU8pxDs8GUHWr5vOZ0YfkKXsBcW3L1q9IoXzq5TZqH8wfwP4oUzv68Ibtfddm+4eJycGXLSpp6Pd29ZdIcNDRNiu27Ruk/8TBHy7kT6rTu36P1X3qfaRWrr4B0iJ4p0fPKoy9JBJyBgewIQ6bZ3sTkTRIylOZwxinYC/oj0bpHdaGynsdSofyMa13UcNZjSgHae2ikGK/NCGVrSYQll7ZGVPqjyAb1d9m2qMLoC1QurRzHvx2g3SNVCEcrexDbvbp/781y8uFaac/iLelfcmyGK0FeP449I5z7V4S4Da8eFaJzYRAveW+Bz3jdib9D2k9upRuEaXus6UaTz2Z2kSZPSgwcPfHJEBRAAAecSgEh3ru91nfmMGTNo9+7dxK8oICATAV8iPXpbNDWt05SK1SxGX0/5Wgj0c3+ci4875+vtl/6wlC5cu0DD6w+n1uVb09RNU2noyqG04N0F1KRUE1JEsKd5q3er1XWUHfHs6bJ7jAtnkfx82uefCofhnfG3Sr8lQlF8FU/hMb7CXVz7zdU7F30S/gmVz1Pe65BHLh6hNyPfJBbqbPuufrs81neiSGcYadKkodOnT4tXFBAAARBwRwAiHetCFwKjRo2i69ev08iRvgWDLgOiExDwk4A3kX700lEqWrEopXsuHe1dsZeO/3qcqn5WlaLaRNFrL74WP0LJYSWFSP9ft//Ri1lfFD/P2y+vuLhna8RWPy15uppywFO9I+4aF+5JYPsr0pUHCE8PCsp4bF2lfJWe2rFXrObDrbtP76bJb032Od8ZW2bQoOWD4uvNbDXT4466U0V67ty5ad26dZQnDzIF+VxQqAACDiUAke5Qx+s9bb6cg/Oj8ysKCMhEwJNI54t4sv83O129eJU2rNlAuTPlplnbZlG/pf3o4qcXn5gCx4Qv+WHJEz+P/C6SPvr6Izr20THKnyW/rlPmUBY+oMm75MGKdNfdcrWhPI46U4zy0OBO0P9fz/+jOW3nUMHnCvqc69rDa6lNVBtRL1XSVLS7727x6q44VaTz5W8TJkwgfkUBARAAAXcEINKxLnQh0KZNG6pYsSK1bt1al/7QCQjoRcCTSC/1dinas3oPTYuZRnVK1BHDeRPpu07teiL1IqctLDOiDA2rN4z6vd5PL3NFP+oQl2DDXdSCX22kIsjdpVzkesoBU/73tp+3Ubt57eibrt/4PU8W6hxLXy53OSqUtZDHdk4V6TVr1qTOnTsTv6KAAAiAAEQ61oBhBJo3by7+s2nWrJlhY6BjEAiEgDuR3uKjFjR36FxqN6YdDWw5ML5bLTvp3Cg8Mpxu379NbSu0FRlYPBVPoSae6quFeTAHR5WYd3fjc79bftoSn35RscXdeH2W9qHYu7EUUVOftJPqeTtVSY//LQAAIABJREFUpNerV49atWpF/IoCAiAAAhDpWAOGEQgPDxd5fxs2bGjYGOgYBAIh4CrSxy4bS92ad6P/tvwvfTniyye6/PHij37HpHPDqO1R1HdJX9o3cJ+IT9da/BHgwaRg9LRbznZ620l3Paj60qCXROhN8ZzFtU7RZ32ninS+V4L/XvIrCgiAAAhApGMNGEbgjTfeoLZt21Lduo/zLaOAgCwE1CJ9x8kdVK5iOXoh7AXausD9gU/eEVeHtijf88FR1wOlV/66QkWHFBUClmPItRZlp1uJP+f27mLIXWPHXb/3NK6n3XKlPvejPizqLiadH1yqj6tOu/vt1jo9v+o7VaS//fbbVL16deJPIVFAAARAACIda8AwAjVq1KAPP/yQ+BUFBGQioIh0FtR5K+Wlvx/+TdtWbaOMKTN6NFOdJz1bmmwiFl3Jk963Vt8n2r00+CVqXKIxTW7mO+uJuwGVfOXKe54yrLCgVor6sCf/zF0edEXw86s6vtzVBj6YyvH1SnHN2b74+8UiVn9GS2PSqzpVpPOmRrly5cTmBgoIgAAIQKRjDRhGoEqVKuLGURZEKCAgAwG+MGbx4sXUt29fioyMpC6Tu9DxPcdp2ZplVCpXKd1MrD62OuXKkEvc3GnHMnHDRNp/br84IGtEWfvOWtq3aB9lSpiJuvzZhVKmTGnEMNL12aFDB3rppZeoffv20tkGg0AABMwnMHv2bMqfPz+VKVMmfnBkdzHfD7YcsXz58vTxxx8Tv6KAQKgJ/PDDDxQe/halSlWIkiR5ns6c+x9d/eM0RXzelTrU7qCreS1ntqSrN6/S9wO+17VfWTrru7QvPXz4kLpU7aK7SR3f6Ujb1m+jZCmSUYJbCehW4lsUExNDlStX1n0s2TrkTx5z5swpPoFEAQEQAIGdO3eKTaURI0bEC3WIdKwLXQiULFlS7FaWKFFCl/7QCQgEQ6Bs2cqUKVNjKlr0X0G+IKYmlaqfjhp0aRBM10+1nbF5Bu36ZRct7bBU135l6WzkmpGUN1Ne+m8BfT8lW/35alo9bTUVyFMgfqqXL1+mR48e0dGjR2WZvmF2REREUPr06alXr16GjYGOQQAErEXAVahDpFvLf9JaW6RIEZo3bx7xKwoIhJLAb7/9Rrlz56euXf98woxz57ZR9P46dOfzJ38eSludPPaznZ6lfNfzxT1MZXoCw/79++nw4cOULVs2W+Ph8MAkSZJQ//79bT1PTA4EQEAbAbVQ5wxQ58+f99hBgrhdjUfKu6zohw8fTlFRUdpGRG3bE9izZw8VLFiQUqRIYfu5YoJyE7h37x7t3XuAIiJuPmHoyZNradnhFnR75hW5J+AQ6xJ0S0AFfy/4lEjn/6CKFi1KSZMmtTWJX375hZ555hnKkSOHreeJyYEACGgnEBb2OKXvV199pU2ke1P02s1AC7sQSJUqFW3YsAHhLnZxqMXnweEuadM2jluP/4a7LFpSl8rWe47ejmhq8dnZw/wlU5dQzNgYKpi/YPyEONzlwYMHdOLECXtM0sssONxl0aJFdPLkSdvPFRO0FgFPtzRbaxbWtTaonXSIdOs63kjL06RJQ6tWrcLBUSMho2+/CfDB0YYN36LUqR8fHL1yhXdnc9CSJQv97gMVjSfAF6Bt2bKFEiZMSAkSJKDY2FghXJ1ycJT/Zv7000/Gg8YIIKCBAES6Blg6V0VMus5A0d1jAi+++CJNnjwZKRixIKQh4JqCkS+OQZGPwPr164kfqjicki9Dc1IKxlu3bhGnXUMBAZkI8Jps2bKlTCY5whZkd3GEm0MzSVxmFBruGNU3AewK+WaEGuYTwGVG5jPHiCAgMwHkSZfZOxa37Y033hA35/FOGAoIyEQAIl0mb8AWhcDbb79N/OlO8+bNAQUEQAAE3BJACkYsDF0IhIeHE8eXcrogFBCQiQBEukzegC0KgUaNGom/l/yKAgIgAALuCECkY13oQoB3g2rWrEnNmjWL748vN/rxxx9p4sSJuoyBTkCACbDo5sL5tRcu9H0QFCId60ZGAvXq1aNWrVrRpUuX8HdSRgc51KahQ4fSxo0b42ev/rdDkYR02hDpIcVvn8HbtGlDFStWpNatW4tJsUDn670LFy4MkW4fN4d8Jp06dRKHlNu3b0/8nwmXgQMHerULIj3kboMBbgjwpkbu3LnpyJEj+DuJFSIFAc6stGnTpvj/s/lv7JUrV/B/eAi9A5EeQvh2GrpHjx6UJUsW4lcWUlwyZsyIX3A7OTnEc+FUde+99x5Nnz6d8ubNS5s3b6ZBgwY9sevjzkSI9BA7zsvw/LeCbxd1V+y+g8d/LytVqiQEOoSQvGvUyZaxaOfLdPz5xNLJnIycO0S6kXQd1PeoUaPo2rVrxK9KwVO4gxaACVN1FeWuot2TCRDpJjgnwCGUB3rXkDj++W+//WZrccC76OvWraP58+dDpAe4ftDMWAIIWTWWrz+9Q6T7Qwl1fBKYMWMG7d69m/gVIt0nLlQIgIDdRfr7Z96n6b9PjydTJ3UdWpFnRfz3ru8PzjqYBj03KP79IZeG0OCLg+O/fy7Rc3SxyMUnSGc9mJUu3b8kfsb998rSiyoer0iufQXgnoCaeBLpiq+HDBkidpvtWPgCuNOnT9OECRMg0u3oYIvPyQm/g1ZwEUS6FbwkmY3KwT21Wfxx7cOHD8UBKIh0yRxmE3PsLNLr/lyXVl5fSY+KPxLe2npzqxDP72V4j6blmEbK+1vyb6EKKSo89f6sq7Oozek2NDPnTGqd/vG5EBbkJZKViBf6/H3WRFlpb8G94n3uc+/tvUK0q9uZuVx8iXQltMlMm8wYiy/aSpo0KT148ECcrUC4ixnUMYa/BJRPKTt27IiMbf5CM6geRLpBYJ3WLR82GTBggIgThkh3mvfNma9dY9IVQe5uN5vf4+Jut1vZWWdhr+yiKyJf8Qi3Z1GviHhF5CvvJ/g+gfinaztzPErx51fchbsoB4TNssXMcX799VcKCwsjfoVIN5M8xvJFADvovgiZ+z5Eurm8bTsaZyjgfL/8CpFuWzeHfGJ2zO7iSUArsBUB7iqwFXHPu+B5k+QVQp6LO7HPgp536l3DX0ocLUEX71986udmOdrbwVH+xM5X5h6z7NR7HD4sy/dK8N9LiHS96aK/QAn4e84n0P7RTjsBiHTtzNDCDQH1zhBEOpaIkQTslifdkwjXItLVIS5KzDm3V8JYvIl0rqeEwBjpN3d9ewp3UVK42vXjdv7kkR9A+BUi3exVh/E8EXDNka7Us3umJZlXBES6zN6xkG3qGEsLmQ1THUBA9uwugYp0d3Hoancqh0R5B37u1bnS7qSzze4uPOOd5kKFCtlyN33JkiU0b9484lcUEAABEPBEACIda0M3ApkzZ6YDBw6IfOkoICALAdlFureYdGbo6X11TLo71moRz+/zwVKrxKSzvbzLznct2DHkZdKkSXT06FGaPHmyLL8msAMEQEBCAhDpEjrFqiaVLl2axo8fT2XKlLHqFGC3DQnILtIZuWt2F/6ZOhuLr+wuimBXi3DXPjn+nIsS2qLEo3N4jKt4N2sZeAp34fF5J/2VV14Rt8varXTv3l1sZvTs2dNuU8N8QAAEdCQAka4jTKd3xf+p1q9fn5o0aeJ0FJi/RASsINIZV7B50l3bc5+uWVvUedKLJytO454fJ2WedCUm3a6xsG+++ab4OxkeHi7RbwpMAQEQkI0ARLpsHrGwPREREZQ2bVrq3bu3hWcB0+1GwCoi3W7c/ZmPt+wudhXozKV48eI0depUKlmypD+YUAcEQMChBCDSHep4I6bNu1/79++nadOmGdE9+gSBgAhApAeEDY0MJJA+fXo6duyYiLlHAQEQAAFPBCDSsTZ0I7BmzRoaN24crVu3Trc+0REIBEsAIj1YgmivJ4Fr165R9uzZ6caNG3p2i75AAARsSAAi3YZODdWUOFtBvXr16Pjx46EyAeOCwFMEINKxKGQiwJ82tmjRgg4ePCiTWbAFBEBAQgIQ6RI6xaomxcbGUpo0aeju3btWnQLstiEBiHQbOtXCU1q2bBnNnDmTVqxYYeFZwHQQAAEzCECkm0HZQWPwgtq6dSvlzJnTQbPGVGUmAJEus3ecZ9uYMWPo7NmzIl0tCgiAAAh4IwCRjvWhK4GaNWtShw4dqE6dOrr2i85AIFACEOmBkkM7Iwi0atWKKlSoQO+8844R3aNPEAABGxGASLeRM2WYCl/OkS5dOurTp48M5sAGECCIdCwCmQhw+sUpU6YQX/6GAgIgAALYSccaMI3AnDlzaO3atTR//nzTxsRAIOCNAEQ61odMBBInTkyc4SVZsmQymQVbQAAEJCSAnXQJnWJlk/bt2ycyFxw6dMjK04DtNiIAkW4jZ1p8KkeOHCG+bZRzpKOAAAiAgC8CEOm+COF9TQQePHhAiRIlonv37olXFBAINQGI9FB7AOMrBKKjo2nx4sX01VdfAQoIgAAI+CQAke4TESpoJVCkSBGKioqiYsWKaW2K+iCgOwGIdN2RosMACfTr14+SJElCAwcODLAHNAMBEHASAYh0J3nbpLm+9dZbVKNGDRH2ggICoSYAkR5qD2B8hUDdunWpdevWVL9+fUABARAAAZ8EINJ9IkIFrQRGjhxJS5cupd27d2ttivogoDsBiHTdkaLDAAnkypWL1q9fT3ny5AmwBzQDARBwEgGIdCd526S5btiwQXycy5caoYBAqAlApIfaAxifCZw5c4bKlClDly5dAhAQAAEQ8IsARLpfmFBJC4E7d+6I9GJ3797F4VEt4FDXEAIQ6YZgRacaCfCh0ZiYGFqyZInGlqgOAiDgVAIQ6U71vMHz5h2j0aNHU+XKlQ0eCd2DgHcCEOlYITIQ6NKlC/F/uHzhGwoIgAAI+EMAIt0fSqijmUC3bt0oU6ZM1Lt3b81t0QAE9CQAka4nTfQVKIGSJUvSuHHjqHz58oF2gXYgAAIOIwCR7jCHmzVdzgM8b948Wr58uVlDYhwQcEsAIh0LI9QEbt68SenSpSMOBXzmmWdCbQ7GBwEQsAgBiHSLOMpqZp4/f55efvllunLlitVMh702IwCRbjOHWnA6nNFl2LBhtGnTJgtaD5NBAARCRQAiPVTkHTBuvnz5xCGpwoULO2C2mKKsBCDSZfWMc+waMmQIxcbG0qhRo5wzacwUBEAgaAIQ6UEjRAeeCLRs2VK8NXv2bEACgZARgEgPGXoM/A8BvtytQ4cOxJcZoYAACICAvwQg0v0lhXqaCbA4X7VqlUg7hgICoSIAkR4q8hiXCXAqWk5Je+3aNUqZMiWggAAIgIDfBCDS/UaFiloJ8KUdBQsWFP85oYBAqAhApIeKPMZlAitXrhRZXb799lsAAQEQAAFNBCDSNeFCZa0ESpcuLfKlv/LKK1qboj4I6EIAIl0XjOgkQAKdOnUS+dEjIiIC7AHNQAAEnEoAIt2pnjdp3gMGDKC///6bRowYYdKIGAYEniQAkY4VEUoCBQoUoAULFohsVyggAAIgoIUARLoWWqirmcDmzZuJLzbau3ev5rZoAAJ6EIBI14Mi+giEwNGjR4kPjZ45cyaQ5mgDAiDgcAIQ6Q5fAGZMP3369HTgwAHxkS8KCJhNACLdbOIYTyEwYcIEOnToEM2YMQNQQAAEQEAzAYh0zcjQQCuBpk2b0muvvUatW7fW2hT1QSBoAhDpQSNEBwESqFOnDrVo0YLCw8MD7AHNQAAEnEwAIt3J3jdp7jNnzqRvvvmGoqOjTRoRw4DAvwQg0rEaQkGALy9KkyYNXb58WbyigAAIgIBWAhDpWomhvmYC169fp7Rp09LVq1fFKwoImEkAIt1M2hhLIRAVFUXLly+npUuXAgoIgAAIBEQAIj0gbGiklQCHvFSuXJnatWuntSnqg0BQBCDSg8KHxgES4AOjHOLXuHHjAHtAMxAAAacTgEh3+gowaf68ozR27Fj67rvvTBoRw4DAYwIQ6VgJZhM4ffq0SLn4559/mj00xgMBELARAYh0GzlT9qk899xztHHjRuK8wSggYBYBiHSzSGMchcCoUaNE2sXIyEhAAQEQAIGACUCkB4wODbUS6Nq1K6VOnZoGDx6stSnqg0DABCDSA0aHhgES4F30cePGiRA/FBAAARAIlABEeqDk0E4zgZ07d4oYTb7gAwUEzCIAkW4WaYzDBPB3DusABEBALwIQ6XqRRD9+EeAdJo5Nf+WVV/yqj0ogECwBiPRgCaK9FgL8iSGnXBw0aJCWZqgLAiAAAk8RgEjHojCVAGI1TcWNweIIQKRjGZhJAGdvzKSNsUDA3gQg0u3tX+lmh6wH0rnE9gZBpNvexdJMEFmspHEFDAEBWxCASLeFG601CeQPtpa/rG4tRLrVPWgd+3EfhHV8BUtBwAoEINKt4CWb2Yib+GzmUMmnA5EuuYNsYh5uVraJIzENEJCIAES6RM5wiimxsbGUNm1akUc4c+bMTpk25hkiAhDpIQLvsGGnTZsm7oGIjo522MwxXRAAAaMIQKQbRRb9eiXQsmVLKl68OHXu3BmkQMBQAhDphuJF5/8QqFKlCnXq1Inq168PJiAAAiCgCwGIdF0wohOtBNasWUMfffQRbd++XWtT1AcBTQQg0jXhQuUACBw/flxcXPTrr78G0BpNQAAEQMA9AYh0rIyQEciRIwetXLmSihQpEjIbMLD9CUCk29/HoZ7h0KFD6erVqzR+/PhQm4LxQQAEbEQAIt1GzrTaVHgn/ezZszRjxgyrmQ57LUQAIt1CzrKgqQ8fPqSsWbMSfzrIl7WhgAAIgIBeBCDS9SKJfjQT4GwI/J/bgQMHKE+ePJrbowEI+EMAIt0fSqgTKAG+QXnXrl04MBooQLQDARDwSAAiHYsjpAT69u1Lf/31F02cODGkdmBw+xKASLevb2WYWa5cuWj+/PlUtmxZGcyBDSAAAjYiAJFuI2dacSqXL18Wu+mcjpEXIwoI6E0AIl1vouhPITB16lRau3YtLVu2DFBAAARAQHcCEOm6I0WHWgl069aNEiZMSJ988onWpqgPAj4JQKT7RIQKARIoWLAgTZ48mTj9IgoIgAAI6E0AIl1vouhPM4HTp09Tvnz56NKlS5Q+fXrN7dEABLwRgEjH+jCCAN+cvGDBAlq3bp0R3aNPEAABEBARBufPn/dIIsGjuKK866syeIJAoATat29PGTNmJE5lhgICehKASNeTJvpSCHAml+HDh1OtWrUABQRAAAQMIeBLd0OkG4IdnboSOHbsGJUuXZouXrxIyZMnByAQ0I0ARLpuKNHRPwQWLlxIU6ZMoU2bNoEJCIAACBhGACLdMLToWCuB1q1bU968eYkzvqCAgF4EINL1Iol+FALlypWjHj16UIMGDQAFBEAABAwjAJFuGFp0rJXAvn37qEaNGmI3nQ+SooCAHgQg0vWgiD4UAsuXLxdhLrt37wYUEAABEDCUAES6oXjRuVYCTZo0oVKlShFnfEEBAT0IQKTrQRF9KAQ4k0vbtm2pWbNmgAICIAAChhKASDcULzrXSmDHjh3UtGlT4owvKCCgBwGIdD0oog8mwJlcevbsSQcPHgQQEAABEDCcAES64YgxgFYC9erVo+rVqxNnfEEBgWAJQKQHSxDtFQKcyeXNN98UO+koIAACIGA0AYh0owmjf80ENm7cKAQ6Z3xBAYFgCUCkB0sQ7ZnA5s2bhTj/6aefAAQEQAAETCEAkW4KZgyilQAfIK1Tpw517NhRa1PUB4EnCECkY0HoQYD/HvEnfB988IEe3aEPEAABEPBJACLdJyJUCAUBzpzA/yGeOHFCXHKEAgKBEoBID5Qc2ikE5syZQ5GRkcRnZlBAAARAwCwCEOlmkcY4mgnwAa3r16/T9OnTNbdFAxBQCECkYy0EQ+DOnTuUL18+ioqKIs7sggICIAACZhGASDeLNMbRTODu3bviP8cvvviCqlatqrk9GoAAE4BIxzoIhkD37t3p1q1bNHXq1GC6QVsQAAEQ0EwAIl0zMjQwk8DcuXNp8uTJtHPnTjOHxVg2IgCRbiNnmjyVXbt2Uc2aNcVh0fTp05s8OoYDARBwOgGIdKevAAvMv27dulS5cmXiHS0UENBKACJdKzHUVwhUq1aNGjRogHSwWBIgAAIhIQCRHhLsGFQLAb44pHTp0uIQ6fPPP6+lKeqCAMJdsAYCIsBnYRYsWECcEhYFBEAABEJBACI9FNQxpmYCAwYMoDNnzhBnWUABAS0EsJOuhRbqMoFr166J8zDLli2jcuXKAQoIgAAIhIQARHpIsGPQQAjkz5+fxowZQ7Vr1w6kOdo4lABEukMdH8S0+X6GxIkT09ixY4PoBU1BAARAIDgCEOnB8UNrEwksWrSIPvroIzpw4ICJo2IoqxOASLe6B821f9OmTfTWW2+J8LrkyZObOzhGAwEQAAEVAYh0LAdLEWjUqBEVLVqU+vXrZym7YWzoCECkh469FUeuUKECtW3bllq3bm1F82EzCICAjQhApNvImU6YCu9ucdgLv+bNm9cJU8YcgyQAkR4kQAc1nzBhAq1du5ZWr17toFljqiAAArISgEiX1TOwyyOB4cOHi5CXmJgYUAIBnwQg0n0iQoU4ApcuXRIbAN999x0VK1YMTEAABEAg5AQg0kPuAhgQCIGwsDDq378/NWzYMJDmaOMgAhDpDnJ2EFPlEJdMmTLRyJEjg+gFTUEABEBAPwIQ6fqxRE8mEvj666+pXbt2tHfvXsqSJYuJI2MoqxGASLeax8y3d968eTRixAg6dOgQJUyY0HwDMCIIgAAIuCEAkY5lYVkCAwcOFGEvy5cvt+wcYLjxBCDSjWds5RGOHTtGxYsXF7HoFStWtPJUYDsIgIDNCECk28yhTpvO66+/TmXKlCG+7AgFBNwRgEjHuvBGoHLlylSvXj3q2rUrQIEACICAVAQg0qVyB4zRSuDcuXNUokQJmjVrFtWqVUtrc9R3AAGIdAc4OcApduvWjX777TficBcUEAABEJCNAES6bB6BPZoJ8NXdnTt3FvHpfPALBQTUBCDSsR7cEZg/fz4NHTpU/N1IkSIFIIEACICAdAQg0qVzCQwKhABnejly5AgtXbo0kOZoY2MCEOk2dm6AUzt+/Lj4BI4PoHO4CwoIgAAIyEgAIl1Gr8CmgAjUrFmT+LZA3EYaED7bNoJIt61rA54Yr4natWtT9+7dA+4DDUEABEDAaAIQ6UYTRv+mEThz5ozYHZs7dy7VqFHDtHExkNwEINLl9o/Z1vXo0YMuXrxIHO6CAgIgAAIyE4BIl9k7sE0zgSVLlhAfBuM40wwZMmhujwb2IwCRbj+fBjqj6Oho4tSt/PchVapUgXaDdiAAAiBgCgGIdFMwYxAzCfTt25c45nTx4sVmDouxJCUAkS6pY0w266effhKftPFBc14TKCAAAiAgOwGIdNk9BPsCIlC9enV65ZVXqE+fPgG1RyP7EIBIt48vg5nJq6++KsLgevbsGUw3aAsCIAACphGASDcNNQYyk8Dp06fFLYILFiyg1157zcyhMZZkBCDSJXNICMzp1asXnT17ljjcBQUEQAAErEIAIt0qnoKdmgksWrRI7Jrt2bMH8ema6dmnAUS6fXwZyExiYmKIQ+C+//57Sp06dSBdoA0IgAAIhIQARHpIsGNQswjwIbHNmzfTt99+SwkTJjRrWIwjEQGIdImcYbIpGzZsIA5z4d//KlWqmDw6hgMBEACB4AhApAfHD60tQKBTp050/vx5XHRkAV8ZYSJEuhFU5e9z3759QqBPnz6dGjZsKL/BsBAEQAAEXAhApGNJOIJA8+bNKXHixDRz5kxHzBeT/JcARLrzVgOfSalatSpFRETQu+++6zwAmDEIgIAtCECk28KNmIQ/BF5//XUqWLAgffrpp/5URx2bEIBIt4kj/ZzG9evXhUAPDw8nPjCKAgIgAAJWJQCRblXPwW7NBG7fvi0+/ubrwPv166e5PRpYkwBEujX9FqjVnM2JMzuNHDky0C7QDgRAAASkIACRLoUbYIRZBC5cuCCEeufOnalDhw5mDYtxQkgAIj2E8E0eunHjxpQmTRqaNm2aySNjOBAAARDQnwBEuv5M0aPkBA4fPiyE+rhx46hp06aSWwvzgiUAkR4sQWu0b9++PV29epU45SIKCIAACNiBAES6HbyIOWgmsGXLFiHUV65cSXw7KYp9CUCk29e3ysw4Dzrfh7B+/Xr7TxYzBAEQcAwBiHTHuBoTdSWwYsUKatasmcihXKpUKQCyKQGIdJs69p9pffLJJ7Rw4UL63//+J0JdUEAABEDALgQg0u3iScwjIAJRUVHEFx6xUM+bN29AfaCR3AQg0uX2TzDWff755+KAKAv0XLlyBdMV2oIACICAdAQg0qVzCQwym8DYsWOJxToL9QwZMpg9PMYzmABEusGAQ9T94sWLRQ50FujFihULkRUYFgRAAASMIwCRbhxb9GwhArybvnnzZlq+fDmlTp3aQpbDVF8EINJ9EbLe+2vXrqVatWqJGHQ+W4ICAiAAAnYkAJFuR69iTgER6N27t9hN/+qrryhnzpwB9YFG8hGASJfPJ8FYtGDBAmrZsqX4PX3jjTeC6QptQQAEHEzg0aNHT8ze9XvlzQQJEjxRz/V7IxFCpBtJF31bjsDo0aNp+vTptGjRInr55ZctZz8MfpoARLp9VsWUKVNoyJAhQqBXqlTJPhPDTEAABEwjoIhx9avrz1wFOgtzRZy7vhppOES6kXTRtyUJsEjnXXUW6lWqVLHkHGD0vwQg0u2xGoYPH05z584VAv2ll16yx6QwCxAAAdMIuIryhw8fEn/xz5V/szFKPUWMP/PMM8Rf/L3632aIdYh005YHBrISARbo4eHhQhA0bNjQSqbDVhcCEOnWXxI9evSg7du3i4uK+D8tFBAAARDwl4BanCti/O+//yb+YqGdKFEiSpgfYih2AAAZ30lEQVQwYbwQV/erCHiue//+fSHgua5SXxHv3MaIMBiIdH+9jHqOI8Dx6SzQP/74Y5FFAsWaBCDSrek3xeo2bdrQ5cuXxQNzsmTJrD0ZWA8CIGAqARbVyhcL9AcPHgixnSRJEkqcOLFmYc193bt3j+7evSvE/bPPPhsv7tUhMXpNEiJdL5Lox5YEfvjhB7Gj/v7771OvXr1sOUe7Twoi3Zoe5p0rfkhOnjw5zZs3z5qTgNUgAAIhI+Aqzlmg8w74f/7zH83i3HUS3PedO3fEbjwLdVexrtekIdL1Iol+bEvgl19+EUK9WrVq4uIUFGsRgEi3lr/Y2t9//10IdI49nzhxovUmAItBAARCSkAR6CyiWZzz7jc/8LOY1rNw37du3RK78tw3PwTouaMOka6nt9CXbQlcv35diIYXXniBpk2bZtt52nFiEOnW8uqJEyfEQzGnVxw6dKi1jIe1IAACISegFugc2sJCOkWKFCIsxYjCYTQ3b94UIl2Jb9dLqEOkG+Ex9GlbAo0aNRJz4wNsKNYgAJFuDT+xlbt27RIPw926daOuXbtax3BYCgIgIAUBdwI9ZcqUQYe3+Jocj/vXX3/pLtQh0n2Rx/sg4EKA49NPnTolUjTidlL5lwdEuvw+Ygv5FlEW6JMnTxaXFaGAAAiAgBYC6hh03kHnmHH+P9qoHXRX23hHnT9155h33lFXMr8Ek/UFIl3LCkBdEPiHQJ8+fWjdunUi9KVkyZLgIjEBiHSJnfOPaVOnTqXOnTuLB9+6devKbzAsBAEQkI6Aki6RBTpnX+FsUCyWzSw89u3bt0X2GLVQD9QGiPRAyaGd4wnMmDFDZH3hnb/27ds7noesACDSZfUMiQtE+Hdo//794oG3WLFi8hoLy0AABKQloA5zYYHOhePQQ1E4Pp0LC/VgD5JCpIfCgxjTNgT27dsnREaRIkWEyOBfSBS5CECky+UPxZrdu3eL350yZcpQZGSknEbCKhAAAUsQYJGuXDjEO9np0qUzPA7dExi25Y8//ojfyVeEeiAgIdIDoYY2IOBCgHfSd+7cSfyxfenSpcFHIgIQ6RI54x9TpkyZIsJb+PflnXfekc9AWAQCIGAZAsouOmdx4Th0FsWcbjGUhdMy8kMDx6dz1pdAs71ApIfSixjbVgS++OILsTM4YcIE6tChg63mZuXJQKTL4z3+T5R/Rw4fPiw+eQoLC5PHOFgCAiBgSQJKLDrnQmdxzLvo/hwWdXdBId8wri7+1HEHjUP5eDedHxY4h7pyiFQrYIh0rcRQHwS8EODY2nbt2lGhQoXELqHZh1bgnKcJQKTLsSr4kyb+3Shfvrw4x4ECAiAAAsEScI1F53j09OnT+9WtPwLcnzqeBrt69aqISw8mNh0i3S9XohIIaCPQsWNH2rp1q9gt5JhblNARgEgPHXtlZBblH374ofh9aNOmTegNggUgAAK2IKDsovOndLGxsWJjzN9QF0WAu+6eewKjtT7v6nO2l6RJk4qQl0B20yHSbbFMMQkZCcyaNUt8tP/ZZ5/RBx98IKOJjrAJIj10buaPn/l34NixY0Kg8wFrFBAAARDQi4A61IWzqqRJk8bvT7C1im6t9VmgX7t2TWSZCTTkBSJdr5WCfkDADYGDBw+Kj/jz588vRAr/oqKYSwAi3Vzeymg7duwQAr1SpUo0adKk0BiBUUEABGxNQMnqwhsCN27coEyZMvkVj85QtIpurfU5Lv23336jVKlSif/7A8nyApFu6+WLyclCoFOnTrRp0yYRp16uXDlZzHKEHRDp5rt54sSJ1KNHD/Fg2qpVK/MNwIggAAKOIMBCmL84qwvf9pktWzap5n3hwgVx6ylneeFwF38OtKonAJEulTthjJ0JzJ49m7p16yZEy7Bhw0ScGorxBCDSjWesjLB3717q16+f+A+T49ALFy5s3uAYCQRAwHEEWKBzqkM+MPrnn3/S888/LxWDc+fOUdq0aeMPj0KkS+UeGAMCTxLg0979+/enVatWCaHeokULIDKYAES6wYDjuuePmnldT58+nYYPH058cBoFBEAABIwmoIh03hjglIc5cuQwekhN/Z85c0akhOSddA53gUjXhA+VQSA0BDZs2CBEDf/ysqgpWrRoaAxxwKgQ6cY6+csvvxRruVq1auLBk2NCUUAABEDADAIQ6RyV/0/xFRtjhkMwBgjYicDYsWOFwOH0dCzWUfQnAJGuP1PukS8k4tCWX3/9VYhzFukoIAACIGAmAXW4C++ks071d7da60FQrfXZtvPnz4vNOCVXur+2+au7E8RpdIh0M1ccxnIcAT5YwkJ927ZtQuw0atTIcQyMnDBEuv50Bw4cSJxbmNcrHxBFAQEQAIFQEFAfHOV0hxkzZhSC2J+iVXRrrc9x8leuXBFpIXFw1B+PoA4ISExg9erVQqznzp1biB9O24gSPAGI9OAZKj0sXrxYrNGSJUuKNZo9e3b9OkdPIAACIKCRgGsKRhbDLIr9KVpFt9b6/NDAsfJIweiPN1AHBCxCYOTIkUIIDR48mAYMGGARq+U1EyI9eN/8/PPPIrSFLyVicV6nTp3gO0UPIAACIBAkAfVlRn/99Rfdvn2bcubM6VeviuhWV3a9fdSfOp4GO336NCVLloxSpkyJy4z88ggqgYBFCJw8eVKIoh9//FGIorp161rEcvnMhEgPzicjRowQD41Dhw4VryggAAIgIAsBRaQ/ePBACHQOL3nhhRfo2Wef9WmiPwLcnzruBmJ7Tp06JcJvWKizPRyPniBBAp92qSv4OguKmHRNOFEZBPQlsGTJEiGM8uXLR126dCEWnCjaCECka+Ol1OZ0iuPHj6dChQqJB0VegyggAAIgIBMBFulKyIuSK51j0kOdZYpvGmV71DnSWaBDpMu0emALCOhEIDIykiZMmCBywHbu3Jlq1aqlU8/27wYiXZuPeZ0p4pzXWtWqVbV1gNogAAIgYCIB15AXFsgvvvii31le9DaVD7Pyp+D8oBBMqAvbhZ10vb2D/kDAQAJRUVFCQPFBFN5Zb9CggYGj2aNriHTffuTDTbyu+KtChQpibZUvX953Q9QAARAAgRATUHbTOcQkNjZW3DyaKFEiypYtW0gs44xt9+/fF7vofLM4h7oEsosOkR4S92FQEAieQHR0tBBU/MTOu53NmjULvlOb9gCR7tmx/J+ZsnNeu3ZtIc6LFy9u05WAaYEACNiVgBLy8v/t3c+LHEUfB+B+b4KioDlEBWN0MSJRJKKop9cX9BLES0ADIhjhPYX3Hwg5SY7v5SWn95CAl0WI4CWICtmoqKgQCCoqxqy/QJAoKHoR5H33W7M929PTM9ObnRlrep6BZn/NTlc9VZt8uqa6KsLxb7/9VsRoerzzfN111821ynHu2GU0RtHj3HGxEDuNbneaS1loI+lzbT4nIzBdgVdffTWFrCtXrqSA9cILL0z3BB14NSF9uBF/+OGH/sj5c889ly70Yu65BwECBBZRoDo3Pd4Z/OWXX9JGa7GbdwTleTziAuHixYvF7t27ixtuuCGtjV4GdCF9Hi3gHAQyFXj99ddT6Iql8iJwHT16NNOSzr9YQvqW+fr6ej+cRz+JC7tYCcGDAAECiy5Qzk2PsBxB/aeffkqj6vv3709heZaPP//8M+3CHKPnN910UwrocXFwNSu6VMtpJH2Wrea1CcxZ4K233koh7KOPPkoBLI55jSLMuaqtTyekF+kmpugXL730UrqIi35xyy23tDb0RAIECOQuUI6mxzTQCOqxJGME9fgY7xTO6v/CONenn36allqMgB4fqwH9akfRw1tIz73XKR+BqxD44IMP0jSYGGF/5pln0hE3BC7jY1lDevyHFfcuxPH222+nYB4B/cYbb1zGbqDOBAgsgUB12ssff/xR/P7770Xs/BlTQu+999602so0H7GB0scff1zs2rUr7XR67bXXpo2LdjrNpSyjkD7N1vJaBDITiOkvEdJefvnltJZsGdhXVlYyK+nsirNsIf3cuXOpvaPdY4WWss3jPw4PAgQIdF2gHtRjxZeYox6j6rG50G233bbj6S8xveXbb79NmyfF6HnMQY+VXKYZ0I2kd72nqh+BisC7777bH1m97777+uFt2iMLuaEvQ0iP6SzlqHm059NPP53aN/4z8iBAgMCyCVSDekxHiY2FYtQ7RtXjuP3224ubb75521Ng4rXixvuvv/46jZzHEf/mxgZK1ZVcdjLFpdpWRtKXreeqL4ENgVdeeSWFutjRtBxpffLJJztp09WQHqNC5Yj5V1991W/HBx98sJPtqFIECBDYjkB1jnqsoR7TX2JUPcJ63FAaR4x+R1ivrsZSPUeMmJerxUQ4j9+Pm0PjiHBejp7HWujlTaLTCuhG0rfT2p5LoIMCP//8c38Etgx6MQr70EMPdaa2XQvpy3SB1ZlOqCIECPwlAmVQr678EmE9RtbjhtII3XHE1zFKHmE+nhuPCNsRvmOEPEbKI5DHETeGxtcxtaV+g+g0A7qQ/pd0GSclkKdAdcpEjBLECPtTTz1V7Nu3L88CtyxVF0J6rNpz5syZdEEV6/5G28TFVNenKrVsYk8jQIDASIEydJdBPVZ/iTAeRwTzCO3l5zFyXg3pcQNoBPEI62Uoj8/LkfPqEovTDuhCuk5NgECjwNraWgqEr732Wrpb/Yknnigef/zx9HHRbkBcxJD+3XffFW+88UY63nzzzeLOO+9MF0wRzpfppl9/ngQIEJiWQDWsVwN7hPbyKEfey5H0CN4RxOtHfL8M5bMI52WdzUmfVut7HQIdFbhw4UI/ML7zzjv9sB6B/Z577sm+1osS0mNVlgjkEcxjW+nqhdGtt96avbMCEiBAYBEEqmE9ylsN5uXPynpUg3g9lM8ynAvpi9CTlJFAZgK//vrrwAhvvFX4yCOPFI8++mj6+PDDD2dW4qLIMaTHvQDvv/9+8d577/U/3n///SmYx7Gsa9pn13kUiACBzgrUA3n963pQH/X1LIGMpM9S12sT6LjA5cuXB8LmZ599NhDaDxw4kO6c/ysfOYT0zz//vPjwww/7oTxu0q1e3MTnsbqABwECBAgQMJKuDxAgMHWB2DCiOkJ88eLFtGlE7PS2f//+9LE84u74eTzmGdJ//PHHtPtceXzyySfp85iu8sADD/TfcbBM4jxa3jkIECCw2AJG0he7/ZSeQPYC33//fQqqZWAtA2ysGnPXXXelTSXqxzRHlacd0suNLNbX19OGFuURq+PEUl7VC5HywsQqLNl3UwUkQIBAdgJCenZNokAEui8Qc/8itH/55Zf9kFsNvddcc00K7rFjZmy5HMeuXbuGPo/vxZq1seJM3H3f9BgX0ssNLsoto69cuZK2jo6j+nmMkJdh/Prrrx+4qNi7d2/6+u677y727NnT/cZTQwIECBCYi4CQPhdmJyFAYDsCEYojtMcofD0wV8Nz/Cw2pIh1bmNaTYT1OGI5rdicolwma/fu3ek55SYW5ccI9vH8CN7Vi4Cmi4JytD/WkPcgQIAAAQKzFhDSZy3s9QkQmItArDQTwbwexJ999tlidXU1hfFyl7jyYwR7DwIECBAgkKOAkJ5jqygTAQJTE5j2nPSpFcwLESBAgACBMQJCuu5BgECnBYT0TjevyhEgQKCzAkJ6Z5tWxQgQCAEhXT8gQIAAgUUUENIXsdWUmQCB1gJCemsqTyRAgACBjASE9IwaQ1EIEJi+gJA+fVOvSIAAAQKzF9h2SJ99kZyBAAECBAgQIECAAIFYinjU428bm478DxEBAgQIECBAgAABAvkICOn5tIWSECBAgAABAgQIEEgCQrqOQIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgMwEhPbMGURwCBAgQIECAAAECQro+QIAAAQIECBAgQCAzASE9swZRHAIECBAgQIAAAQJCuj5AgAABAgQIECBAIDMBIT2zBlEcAgQIECBAgAABAkK6PkCAAAECBAgQIEAgM4GhkP7N6UPFYy9eqBXzQHF87Uzx/J7Zl/78sTuKkytrxZnNk9W/nn0JdnCG88eKO46sDr7A4VPF5RN/38GLjv7VrbY6XJy6fKJoOkv4HVkd/fM2BUvnuXR0cj3mXP82ZfccAgQIECBAgMAiCjSH9DaBrE1tI7SdXCnWzjxftM33E0P6Vbxmm6Lu7DnfFKcPPVa8eKEehs8Xxw6tF//cRv2Lpvo1fe+b08Whx84WB+dw8TQ5pE+x/vWGyLK9d9Zb/DYBAgQIECBAYJKAkD5JqMXPU4g9e3BbFyMjX3ZbIf1ScXTECHqLYrd+yqSQPtX6C+mt28UTCRAgQIAAge4KbDOk90ZMLx09VRRHjhSrxebI8cA0h97UmL3/jWkWFbjKtI/BKTWDU2nGjaT3pm40v2b53fScYnCKST1EDk3pGZiSUtZxrVg5GaPj8crjpvtsjJbfcaTYmG9StJnVMu7cTfU7tVGbep3XVk4OTklK5d/b2DYbhRuYPhS1GecfPx8ox4HjxamDZ4sjI99daVv/eN7JYqU68p/eDSgvNIb71r8Orxb/GWrvsp7j22d0HUf04e7+jasZAQIECBAgsIACVxXSz26E84P/PtGbo16fdnH+dHF67/O9nzWMCg+NuqaAHxm3N6d6x9Ndhs5ZhrJeiO6Ft32VOdybUzX2lcG+nLqxFcxTaP3iePNIea384/rA5HM3mzVOgRkIuCl6p5A+0DYNnm38B+paXoCNmlvfuv7tQnq9/MN1n9w+4+vY7LSAf7uKTIAAAQIECHRYoN2Noxujqb155ZsB5+DWjZ29kD5i2sVQYG4IapuveeloL0TvOKQXtXMMlK/p/OWFxuCI7tnt1LFykZHi8sDNt+U89TbnnkJIr5Z7KKRP8m8uY9O7E/2/iYaQ3rr+DSPpA+5xkhEXXaPbZ1IdG/pwh//AVY0AAQIECBBYTIGrGkkvA3WvyuXIZlEcrk/5qAesptU/Nt3K3915SB8M+gPzqUeO+laD3eDIe6+KY27SHDeSXA2hrc6985A+2Da1i55J/nubL7jGzklvW//6xVPftT7dpTZtaMI7I0Pts96wws5AH2to38X821VqAgQIECBAoMMCUwjpmzopkL5YXCjnqce3G0P61tSWJtdphPSt8/6jOJfm0G8Gv1ZBeZshfVyAzzKkj/Ef4TM2pLet/1xD+rg+JqR3+N8zVSNAgAABAp0RmF5Ir4yq96ci1EN6i2UDpxLSy0B46mBx9khlKs6o8zfewFgZ0Z1Q7pHTQaqv2+rcMx5Jn+Q/4udjp7ukIg/frLs1wl36N0xDGbgoGBGetzuSXkxamlJI78y/XipCgAABAgQ6LLDzkL4Roo4VJzZXNqkFoIaR2eHNdTZ+59i54h8nemuptwrptTngI0fkvzhQbNzh2t8YqTe4X9/cpz5HeZsj6enkvRVOVvtz96vvLmxdJEw+92ZIr9evaYR7xI2jY6e7jKp/zX9bN462rn/9Bt1Ns/47L2NC+oDH5PYZ38eE9A7/e6ZqBAgQIECgMwLtbhzdqG5vzviogBTTXHqPA8crN5VW5qtvvEB/x8r6UoPV35kY0ke85lCLpGD7ReNOqfVlEJvKPBB2J41Ab558aAnFvttW6cafO563Ncd/y6zhe1cZ0rcuVLbKNLLN4ikb7ZaWfGyxwdXk+pfBPL1wcWptpTg5tARjfSnLet3LJRjHv9Mxuo8J6Z3510tFCBAgQIBAhwWGQnqH66pqBAgQIECAAAECBBZCQEhfiGZSSAIECBAgQIAAgWUSENKXqbXVlQABAgQIECBAYCEEhPSFaCaFJECAAAECBAgQWCYBIX2ZWltdCRAgQIAAAQIEFkJASF+IZlJIAgQIECBAgACBZRIQ0peptdWVAAECBAgQIEBgIQSE9IVoJoUkQIAAAQIECBBYJgEhfZlaW10JECBAgAABAgQWQkBIX4hmUkgCBAgQIECAAIFlEhDSl6m11ZUAAQIECBAgQGAhBIT0hWgmhSRAgAABAgQIEFgmgf8DwBUOeMp7AWMAAAAASUVORK5CYII=[/img][br][br]Im nächsten Schritt erweitert man auf beliebige Winkel, indem man definiert, dass der Sinuswert eines Winkels weiterhin die y-Koordinate des Schnittpunkts vom 2. Schenkel mit dem Einheitskreis ist und der Kosinuswert die x-Koordinate des Schnittpunkts.[br][br]
Bewege den Punkt P und beobachte die Größe beiden Koordinaten.
Wertebereich
In welchem Zahlenbereich liegen die Sinus- und die Kosinuswerte?
Winkel mit gleichen Sinuswerten:
Gesucht wird der Winkel [math]\beta[/math] aus dem Intervall (0°, 360°], der den gleichen Sinuswert wie [math]\alpha[/math] hat.[br]Tipp: Symmetrie ausnutzen ;)
Frage 1:
[math]\alpha[/math] = 32°[br]Der Winkel [math]\beta[/math] hat den gleichen Sinuswert wie der Winkel [math]\alpha[/math].[br]Wie groß ist [math]\beta[/math]?
Frage 2:
[math]\alpha[/math] = 32°[br]Der Winkel [math]\beta[/math] hat nun den gleichen [b]Kosinus[/b]wert wie der Winkel [math]\alpha[/math].[br]Wie groß ist [math]\beta[/math]?
Frage 3:
[math]\alpha[/math] = 210°[br]Der Winkel [math]\beta[/math] hat den gleichen Sinuswert wie der Winkel [math]\alpha[/math] . Wie groß ist β?[br]Tipp: Obiges GeoGebra-Applet ist evtl. hilfreich.
Gleiche Kosinuswerte
Entsprechend gibt es zwischen 0° und 360° jeweils zwei Winkel mit dem gleichen Kosinuswert.[br]Das folgende GeoGebra-Applet veranschaulicht das.[br]Um beide Winkel zu finden, nutzt man die Symmetrie zur x-Achse aus.