Being famous as an architect Le Corbusier became an ambassador for Ghyka and the ideas of Zeising. He knew and admired the publications of Ghyka as a '[i]revelations of the laws of our being and our world, so noble of nature and inaccessible that it takes a lot of work and intellectual stubbornness for who's searching fo truth, deep enough to give you the key of the world.'[/i][br][br]Le Corbusier also writes that in Renaissance it was proved that the human body follows the golden section. So he was clearly poorly informed. Before Zeising (1854) nobody ever saw golden proportions in any body.

The challenge to create a modular system as an architect have to be seen within these ideas.[br]In 1948 he presented his Modulor, from the words Module and 'or' (French for gold).[br]A friend would have suggested him to start from a man of 'six feet tall' (182.88 cm).[br]But don't confuse his famous drawing with the Vitruvian man or the man of Zeisling. Le Corbusier doesn't illustrate the height of the knee or the chin. Zeisling already did this. Whereas da Vinci and Zeisling examine the proportions on the human body, in the drawing of the modulor the human body is just the start to tranform [math]\varphi[/math] into in concrete dimensions.[br]In the table below you can read how increasing powers of [math]\varphi[/math] produce smaller numbers. [br]Taking as a unit [b]1.829 m, the upper edge of the hoofd[/b], increasing powers produce a sequence of decreasing numbers.[br][list][*]sequence 1[br]Sequence 1 starts with applying [math]\varphi[/math] on the lenght of the man. [br]The navel matches [math]\varphi[/math]=1.130 m etc. This is the row of numbers on the left.[br][/*][*]sequence 2[br]A second golden rectangle is created between navel and the upward stretched hand, in which the head lies at the height [math]\varphi[/math]. [br]The distance between head and stretches hand becomes 1+[math]\varphi[/math] . (1 - [math]\varphi[/math]).[br]Translated into dimensions you get 1.829 m + 432 mm = 2.260 m.[br]Multiplying this height with powers of [math]\varphi[/math] you get the numvers on the right.[/*][/list]

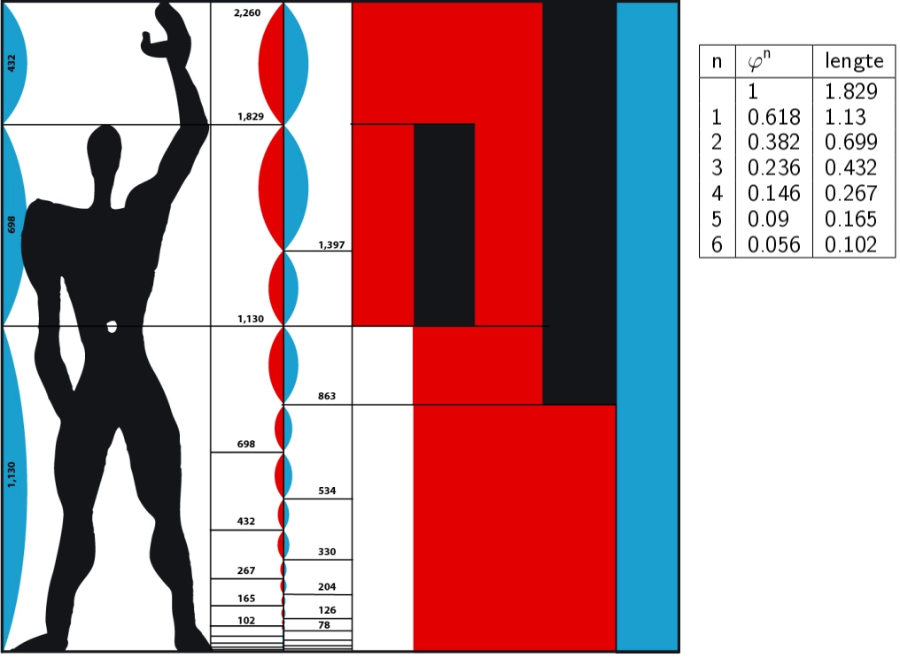
The sequence of number can be continued infinitely. This produces so much combinations that you can realise eny distance, while pretending any distances are linked by just one proportion.[br]In fact it's not different from starting with one meter, dividing it into dm, cm and mm.[br]Of every distance you can say it approximately equals ... centimeter. It only sounds less mysterious than a proportion [math]\varphi=0.618[/math].

While the Parthenon and the renaissance architecture of Palladio and Alberti don't have anything in common with the golden section, it does appear in modern architecture. The reputation of Le Corbusier can have played a role in it, but there's more. [br]An interessenting article on moderne architectuur is '[url=https://www.researchgate.net/publication/374131589_Applications_of_the_Golden_Mean_to_Architecture]Applications of the Golden Mean in Architecture[/url]' by Nikos A. Salingaros. He makes a clear difference between the mythical reputation of the golden section as an esthetical ideal ant the use of a hierarchical modular system: "[i]artists and architects have long made extraordinary assertions about a preference for rectangles having aspect ratio 1.618:1 approximating the Golden Mean. Such claims are false and are chiefly due to failing to measure things accurately. These embarrassing errors are perpetuated by a kind of cult mysticism. The Golden Mean does apply to architectural composition in the context of scaling hierarchy that organizes complexity; this design methodology is unrelated however to a rectangle’s aspect ratio. Simply considering rectangular aspect ratios does not guarantee good design.[/i]" [br]An interessenting quote in the article is that in prestigious projects architecten are flourishing to governements and rich clients with 'non-linearity, fractals and golden ratio' as a 'selling argument'. [br]So there you are as a simple mathematician who tries to illustrate the use of the golden ration in practice...