
Função Logarítmica e Exponencial
Resumo sobre Funções
Função Logarítmica
[br] Toda função definida pela lei de formação [math]f\left(x\right)=log_ax[/math], com a ≠ 1 e a > 0, é chamada de função logarítmica de base [b]a[/b].[br] Nesse tipo de função, o domínio é representado pelo conjunto dos números reais maiores que 0 (zero) e o contradomínio, o conjunto dos reais.[br] O logaritmo é usado para descobrir o valor do expoente de uma base qualquer. Assim, o logaritmo de um número [b]b[/b] com base [b]a[/b], é o expoente [b]x[/b], que é potência da base e resulta em [b]b[/b].

Fonte: [url=https://matematicabasica.net/funcao-logaritmica/]Matemática Básica - Função Logarítmica[/url]
Mapa Mental
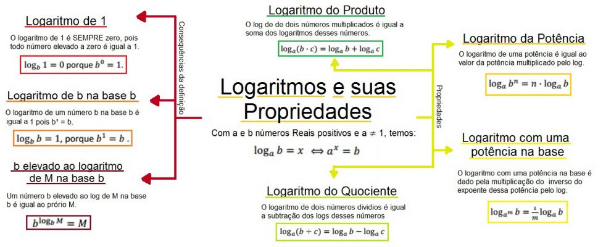
Fonte: [url=https://descomplica.com.br/blog/matematica/mapa-mental-logaritmos/]Descomplica - Mapa Mental Logaritmos[/url]
Gráfico da Função Logarítmica
[br] De uma forma geral, o gráfico da função [math]y=log_ax[/math] está localizado no I e IV quadrantes, pois a função só é definida para x > 0.[br] Além disso, a curva da função logarítmica não toca o eixo y e corta o eixo x no ponto de abscissa igual a 1, pois [math]y=log_a1[/math] = 0, para qualquer valor de a.
Caso: a>1
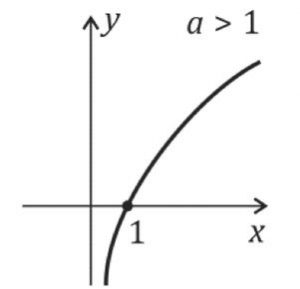
Caso: 0<a<1
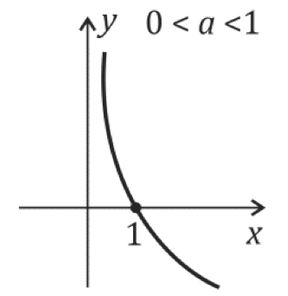
Questão 01 - Sobre a equação a seguir, marque a alternativa correta.
[math]log(x-3)+log(x+2)=log14[/math]
Questão 02 - Responda as questões a seguir:
a) [math]log_{25}0,2[/math]
b) [math]log_{0,2}0,008[/math]
c) [math]log_{0,3}0,09[/math]
Questão 03 - Resolva a seguinte equação:
[math]log_3\left[3+log_2\left(x+1\right)\right]=1[/math]
Questão 04 - Determine o domínio da função logarítmica:
[math]f(x)=log(5x-4)[/math]
Função Exponencial
[br]A função exponencial pode ser caracterizada como uma extensão do processo de potenciação para expoentes não inteiros. Quando [b]n[/b] é um número natural maior do que 1, a potência [math]a^n[/math] indica a multiplicação da base [b]a[/b] por ela mesma tantas vezes quanto indicar o expoente [b]n[/b]
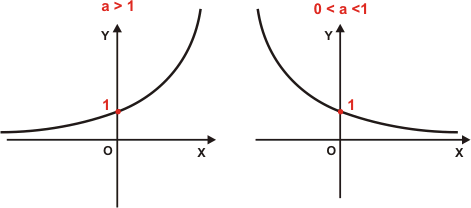
Questão 01 - Calcule o valor de a (Considere uma função crescente)
[math]g(x)=(3a+16)x[/math]
Questão 02 - Dadas as funções:
[math]f(x)=2x^2-4[/math] e [math]\text{g(x)=4x^2-2x}[/math], se satisfaz [math]\text{f(x)=g(x)}[/math], então 2x é:
Questão 03 - A soma das duas soluções da seguinte equação é:
[math]2x^2-14=\frac{1}{1024}[/math]
Questão 04 - O produto das raízes da equação exponencial a seguir é igual a:
[math]3.9^x-10.3^x+3=0[/math]