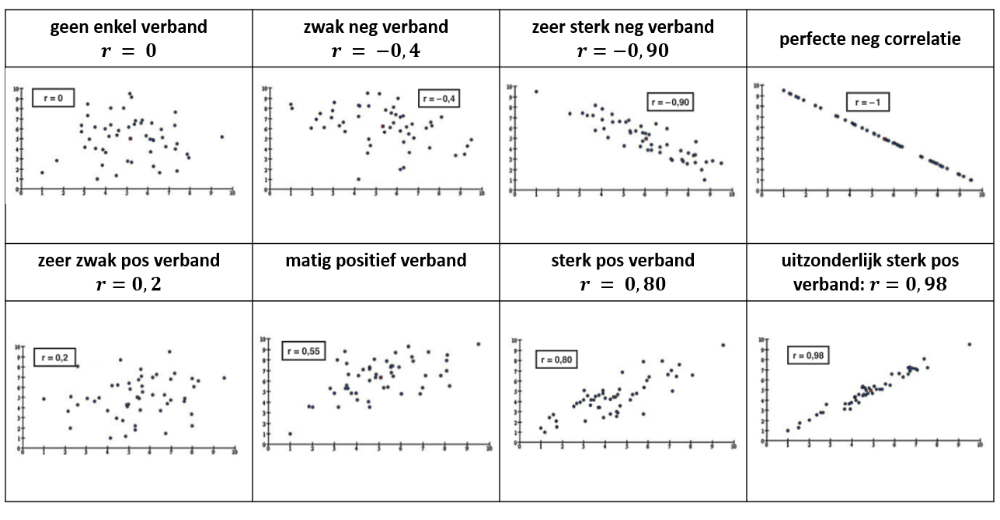
Bestudeer aandachtig de [b]theorie blz 220-221.[br][br]Doelen [/b]: [br][list][*]Je kent het begrip correlatiecoëfficiënt.[/*][*]Je kan de sterkte van een lineair verband zowel grafisch als numeriek interpreteren.[/*][*]Je kan met ICT de correlatiecoëfficiënt bij een lineair verband bepalen.[/*][*]Je kan de betekenis van de correlatiecoëfficiënt bij een lineair verband verwoorden.[/*][/list][br]We onthouden: [br][br][b]De correlatiecoëfficiënt r is een maat voor de lineaire samenhang tussen twee variabelen.[br][/b][br][list][*][math]-1\le r\le1[/math][/*][*][math]r>0[/math] → stijgende regressierechte[br][math]r<0[/math] → dalende regressierechte[br][math]r=0[/math] → geen lineair verband[/*][*]Hoe dichter [math]|r|[/math] bij 1 ligt, hoe sterker het lineair verband en hoe dichter de punten bij de rechte liggen.[/*][/list]Afspraak: [br][list][*][math]|r|<0,3[/math] → geen of zeer zwakke correlatie[/*][*][math]0,3<|r|<0,5[/math]→ zwakke correlatie[/*][*][math]0,5<|r|<0,7[/math]→ gemiddelde correlatie[/*][*][math]|r|>0,7[/math]→ sterke correlatie[/*][/list][br][b]Opmerkingen[/b][br][list][*]De correlatiecoëfficiënt [math]r[/math] is enkel een manier om de richting en sterkte van een [i]lineair [/i]verband cijfermatig uit te drukken. Het berekenen en interpreteren van de correlatiecoëfficiënt bij andere verbanden is volkomen zinloos.[/*][*]Als [math]r[/math]in de buurt van 0 ligt, is er geen lineair verband, maar kan er wel een ander verband zijn tussen beide variabelen.[/*][/list][br]Met [b]geogebra [/b]kan je de correlatiecoëfficiënt berekenen via de knop [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAACcAAAAlCAYAAADBa/A+AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAAAPZSURBVFhH1ZhLKHxxFMe/M/6ekdfCKySUBUJZ2FtIWEgWSnZYElbyyCOvsqJIUeRVSMQGK1lYkIiFRzZehTzzjPnfc/yuedwZc2cy85//p25zf7/fdM/3nt8553e6mufnZx1cFM3Hx4frivv8/HRdcToJce9yaMWvS2LRc4+Pj7i7u8Pr6ysc5VyNRgNPT0/4+/vD19dXzOoxK+76+hpSFiMwMBA+Pj78EEdApp+ennBzcwNvb28EBweLlS8U4shjt7e3iIiIcJgoU0jC6ekpAgICjDyoiDnaSvKYs4QRZItskm1DFOIoxmgrnQ3ZJNuGKMSRi53pNRmyaRJh/1kpOTo6QmxsrBjpOTw8hHTUiZF5YmJi4OHhIUa2Y2pblbixsTFMTEyIkWVSUlLQ1NQkRrZjl7ja2lrs7OwgKSkJISEhPEcxYnitrq5yQM/MzPC6PShskzhDpO0Td3rm5+d1ubm5urKyMp2U7mLWmPLycl1eXp4Y2YepbVUJkZOTg6ysLJydnaG5uRlvb29iRU9ycjISExPF6JcQIr8x5zmC+j4pntiDLS0tOmq1fhu7PEdotVrU1NQgPj4e6+vr6O/vFyuOw6Y65+Xlhfr6eoSGhmJxcRFTU1NixRjppVFdXY3BwUExo2d3dxelpaXY2toSM5axuQhTe9PQ0AA/Pz+MjIxgY2NDrOiRthz39/eYnZ3F3NycmAWurq7Q3t6Oi4sL3glr2CyOIM9FRUWxh8iQKW5ublx+yNNDQ0PY3t7G+/s72tra+HDPz8/nBLKGXeJ6enp4eyj+MjMzxawx0dHRqKysZC92dHSgu7sbBwcHSE1NRUlJifjXz9gsbnx8HCsrK+w9ij/qZC2RkZGBwsJCPDw8YG1tjQs4JRUVbTXYJG55eZnFUbw1NjZy/FmDjjRZDDWw5tpxS6gWt7m5id7eXj7Y6+rqEB4eLla+2Nvb4xJjCLX7tKUUm0FBQfyM6elpsWodVeKOj485yyh+qqqqkJCQIFb0DAwMoLOzU4zwnQDU8hcUFKC1tZUbyuHhYRapBlXiRkdH8fLyguzsbERGRuLk5ERx0aFPgmT6+vqwv7+PtLQ0FBcX85bSixFdXV04Pz/n+5/4I35VsbCwwJcl3N3d+ZfKy9LSEicNFWM55tLT01FUVMQvOzk5iYqKCp63hKqW6fLykqs9bauM3CoZ3lNZoVJBj6TkoUYgLCyM/yMjr8XFxXFzaohdLZOzsPvg/xcoxNH2SKLFyHmQTTlMZBTiqOLTJwJnQzZNTxuFOKr69O3Cmd4jW2TT9MRRZCvhsh9yZP79JzDgL93dhVoVSAHBAAAAAElFTkSuQmCC[/img]. Je krijgt een tabel met statistische getallen zoals gemiddelde, mediaan, standaardafwijking en ook de correlatiecoëfficiënt r.[br][br]Enkele [b]voorbeelden[/b]: