Criterios de Congruencia para Triángulos
Este libro se realizó con las hojas de los participantes del taller.
Table of Contents
- Introducción
- Congruencia de triángulos
- Criterio de congruencia LAL
- Criterio de congruencia ALA
- Criterio ALA (ángulo-lado-ángulo)
- Criterio de congruencia LLL
- Criterio de congruencia LLL
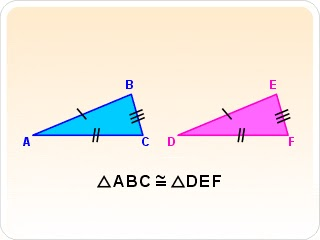
Congruencia de triángulos
Se dice que dos figuras son congruentes si una la podemos poner sobre la otra. Con ello se satisface que ángulos, lados, alturas, medianas, bisectrices, área y perímetro tienen la misma medida.[br][br]Para que dos triángulos sean congruentes existen tres criterios de congruencia que se detallan posteriormente, estos son:[br][br]1. Criterio LAL: Lado, ángulo lado.[br][br]2. Criterio ALA: Ángulo, lado, ángulo.[br][br]3. Criterio LLL: Lado, lado, lado.
Criterio ALA (ángulo-lado-ángulo)
¿Cómo construir triángulos congruentes empleando el criterio ALA?
Realiza la prueba del arrastre en la siguiente applet
¿Son congruentes los triángulos?
Realiza la construcción de un par de triángulos congruentes empleando el criterio ALA
Criterio de congruencia LLL
Si tres lados de un triángulo son congruentes, respectivamente, a tres lados de otro triángulo, entonces los triángulos son congruentes[br][br]Observa la siguiente figura y posteriormente responde las preguntas.
1. ¿Puedes concluir solo observando la figura anterior si estos son congruentes? (No puedes modificar la figura ni medir).
2. Si utilizas la prueba del arrastre, ¿puedes concluir que los triángulos son congruentes?
3. ¿Qué propiedades se utilizaron para la construcción de la figura? ¿Satisface el criterio LLL?
Con lo anterior, construye dos triángulos utilizando el criterio LLL
Para retroalimentar...
En el siguiente video puedes observar otra construcción de triángulos congruentes mediante el criterio LLL.
¿Hubo alguna diferencia en la construcción del video con la del primer applet?, ¿que puedes concluir?
Para saber más...
