Stage 5.1 Similar Shapes
A basic introduction to similar figures and using scale factors to calculate matching sides.
Table of Contents
- Introduction
- Investigating Basic Similarity
- Copy of Similar Figures: Dynamic Illustration
- Properties of similar shapes
- Properties of Similar Shapes
- Scale factors
- Calculating Scale Factors
- Using Scale Factors for enlargements
- Calculating Sides
- Calculating sides in similar shapes Q1
- Calculating sides in similar shapes Q2
- Calculating sides in similar shapes Q3
- Calculating sides in similar shapes Q4
- Calculating Sides in Similar Figures
- Special Cases
- Investigating Similarity of squares and circles
- Investigating Similarity of regular polygons
- Working with similar shapes
- Properties of Dilations
- Scale Drawing 7.G.1
- Making Scaled Copies
- Practice: Corresponding Parts and Scale Factors
- Listing matching sides and angles in similar triangles
- Using Scale Drawings
- Copy of IM 7.1.7 Lesson: Scale Drawings
Investigating Basic Similarity
What makes 2 shapes mathematically similar?
Use the small cross (x) to see different pairs of similar shapes, and then complete the tasks that follow.
You can change the shape by moving the blue dots.
Similar shapes have the same:
Similar shapes have different:
[b][u][color=#0000ff][size=150][size=200]Written Task - complete in your workbook.[/size][/size][/color][/u][/b][br][br]1. Write the heading "Similar Shapes".[br]2. Copy and complete the following definition [br] ([color=#ff0000]check with the teacher if you are unsure of the correct answers to use[/color]):[br][br] [color=#0000ff] "Similar shapes have the same _______ but different _______. "[/color][br]3. [color=#ff0000]Copy one pair of similar shapes[/color] from the Geogebra investigation completed above.
Properties of Similar Shapes
Change the similar shapes in the activity below and answer the questions that follow.[br][br][color=#9900ff][b]Keep an eye on angles and the ratios comparing the matching sides.[/b][/color]
You can move the blue dots, or change the size of angles A and B using the sliders.
What did you discover? Use the Geogebra investigation to answer the following questions:
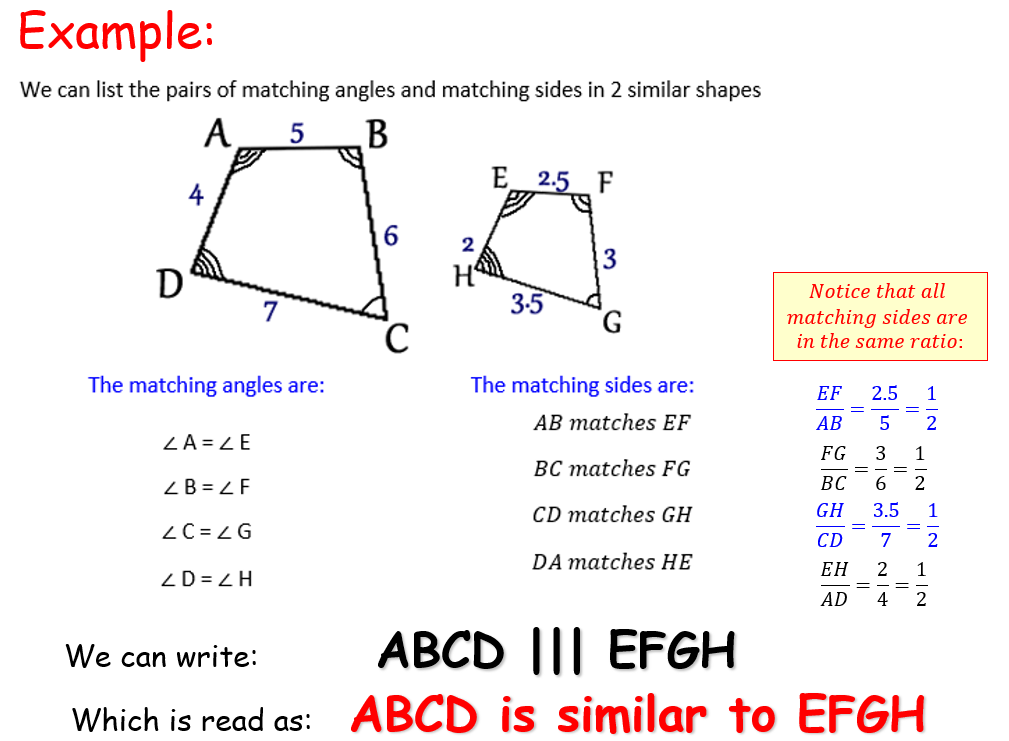
The matching angles in similar shapes are:
The matching sides in similar shapes are:
[b][color=#0000ff][size=200]Written Work - complete the following tasks in your workbook.[br][/size][/color][/b][br][br]
Copy the following notes and examples into your workbook
Calculating Scale Factors
The ratio between matching sides in similar shapes is known as the SCALE FACTOR.
Written Work First - copy the following notes into your workbook
[color=#0000ff][size=200]Special Notation[/size][/color][br][br]The new shape is known as the IMAGE of the ORIGINAL.[br]Use the link below and then [color=#ff0000]copy the example and description into your workbook:[/color][br][br][b][url=https://schoolsnsw-my.sharepoint.com/:i:/g/personal/marc_azara_det_nsw_edu_au/EQm7r0EZAwRIhorzDce_HRcBTb-PQrtXaDjVl_KGN1QQMw?e=s6bJey][color=#9900ff]LINK to original v image EXAMPLE [/color][/url][br][br][br][/b][color=#0000ff][size=200]Scale Factors[br][/size][/color]The ratio between matching sides is known as the SCALE FACTOR.[br][br][left][size=150]Scale Factor = Image length [math]\div[/math][/size] Original length [size=150][size=200][br][math][/math][/size][/size][/left]
Use the slider to change the scale factor. Move the blue dots to change the shape.
What did you discover? Use the Geogebra activity to help answer these questions:
When the [color=#ff0000]scale factor is less than 1[/color], the image created is:
When the [color=#ff0000]scale factor is equal to 1[/color], the image created is:
When the [color=#ff0000]scale factor is greater than 1[/color], the image created is:
Calculating sides in similar shapes Q1
[color=#0000ff][size=200]Written Work - Copy the notes, examples and questions in your book.[/size][/color][br][br]WE can use the scale factor to calculate unknown sides in the image or the original.[br][br][url=https://schoolsnsw-my.sharepoint.com/:i:/g/personal/marc_azara_det_nsw_edu_au/EW-e4f6Yg5VMtYlWy_j5l2wBGQfXxOzi7ABMiyGb3ZbMUw?e=gr0aYG][color=#9900ff]LINK for notes and example to copy[/color][/url][br][br][br] [br][br]
Answer each of the following questions:
What type of Scale Factor is represented?
Type a number only for your answer:
The Scale Factor is:
Type your answer without the units. e.g. Type "2.5", NOT "2.5cm".
The length of a is
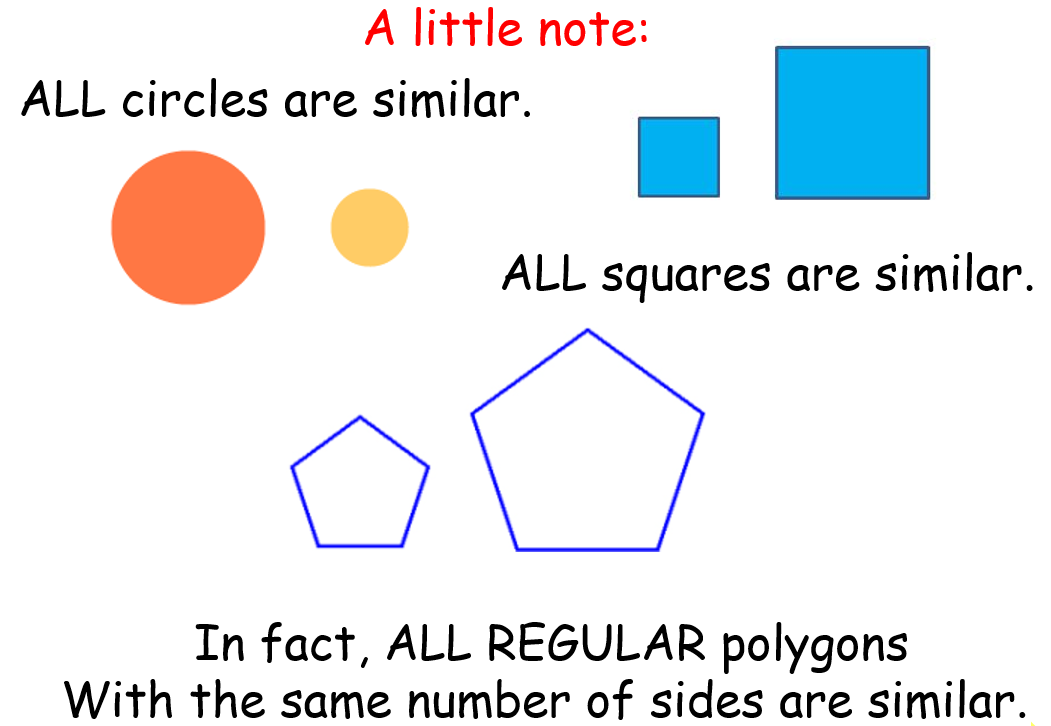
Investigating Similarity of squares and circles
[size=150][color=#ff0000]Are all circles similar to each other? [/color][/size]
Move the slider to see that all circles are enlargements or reductions of each other.
[size=150][color=#ff0000]Are all squares similar to each other? [/color][/size]
You can change the size and orientation by moving the red dots.
What did you discover?
Are all circles similar to each other?
Are all squares similar to each other?
Properties of Dilations
This applet accompanies the [b]Introduction to Dilations[/b] activity given to you in class. [br]Have fun with this!