
Sistem Persamaan Linear Dua Variabel
Sistem Persamaan Linear Dua Variabel
[br]










Diketahui sistem persamaan:[br]x + y = 5[br]x - y = 1[br]Nilai dari x dan y yang memenuhi sistem persamaan tersebut adalah:
Tentukan himpunan penyelesaian dari SPLDV berikut:2x + y = 7x − y = 1
SPLDV berikut:[br]x + 2y = 6[br]3x + 4y = 18[br]Diselesaikan dengan metode eliminasi. Nilai x adalah:

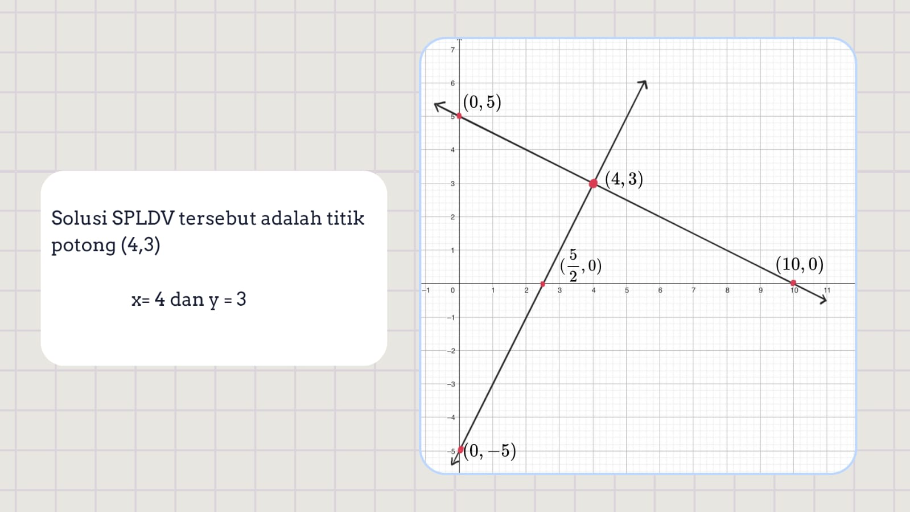
Amatilah grafik yang menunjukkan dua garis yang berpotongan di titik (2, 1)(2,1). Apa hubungan antara titik potong tersebut dengan penyelesaian dari SPLDV?
Perhatikan langkah berikut:[br]2x + y = 10[br]4x + 2y = 20[br]Jelaskan mengapa kedua persamaan ini sebenarnya memiliki solusi tak hingga.
Diketahui dua garis berpotongan. Misalkan kita tarik kedua garis tersebut sepanjang mungkin, apakah akan tetap berpotongan? Jelaskan

Jelaskan perbedaan antara metode substitusi dan metode eliminasi dalam menyelesaikan SPLDV. Dalam kasus apa masing-masing metode lebih efisien digunakan?
Bagaimana cara kamu mengetahui bahwa suatu sistem persamaan memiliki:[list][*]Satu solusi[/*][*]Tak hingga solusi[/*][*]Tidak ada solusi[/*][/list]
Berdasarkan pengamatanmu terhadap penggunaan media GeoGebra dalam menyelesaikan SPLDV, simpulkan bagaimana media ini membantumu memahami konsep sistem persamaan dua variabel.
Visualisasi Grafik SPLDV
MATERI SPLDV
[justify][b]A. Capaian Pembelajaran[br][/b]Di akhir fase D peserta didik dapat mengenali, memprediksi dan menggeneralisasi pola dalam bentuk susunan benda dan bilangan. Mereka dapat menyatakan suatu situasi ke dalam bentuk aljabar. Mereka dapat menggunakan sifat-sifat operasi (komutatif, asosiatif, dan distributif) untuk menghasilkan bentuk aljabar yang ekuivalen. Peserta didik dapat memahami relasi dan fungsi (domain, kodomain, range) dan menyajikannya dalam bentuk diagram panah, tabel, himpunan pasangan berurutan, dan grafik. Mereka dapat membedakan beberapa fungsi nonlinear dari fungsi linear secara grafik. Mereka dapat menyelesaikan persamaan dan pertidaksamaan linear satu variabel. Mereka dapat menyajikan, menganalisis, dan menyelesaikan masalah dengan menggunakan relasi, fungsi dan persamaan linear. Mereka dapat menyelesaikan sistem persaman linear dua variabel melalui beberapa cara untuk penyelesaian masalah.[/justify][br][b]B. Tujuan Pembelajaran[br][/b][list=1][*]Peserta didik dapat dapat mengenali bentuk persamaan linear dua variabel.[/*][*]Peserta didik dapat menggambarkan grafik dari SPLDV dan menentukan solusi sistem persamaan melalui grafik dengan tepat.[/*][*]Peserta didik dapat menjelaskan langkah-langkah dalam metode substitusi untuk menyelesaikan SPLDVdengan benar dan tepat.[/*][*]Peserta didik dapat menggunakan metode substitusi untuk menemukan solusi dari SPLDV dengan benar.[/*][*]Peserta didik dapat menjelaskan prosedur dalam metode eliminasi untuk menyelesaikan SPLDV dengan benar.[/*][*]Peserta didik dapat menggunakan metode eliminasi untuk menyelesaikan SPLDV dengan tepat.[/*][*]Peserta didik dapat memahami konsep dan cara penggunaan metode campuran dalam menyelesaikan SPLDV dengan benar.[/*][*]Peserta didik dapat mengaplikasikan metode campuran (eliminasi-substitusi) dalam menyelesaikan sistem persamaan linear dua variabel dengan benar dan tepat.[/*][/list][b][br]C. [/b][b]Pemahaman Bermakna[br][/b][justify]Sistem Persamaan Linear Dua Variabel (SPLDV) adalah metode untuk menemukan pasangan nilai dua variabel yang memenuhi dua persamaan linear secara bersamaan. SPLDV dapat diselesaikan menggunakan berbagai metode, seperti grafik, substitusi, eliminasi, atau kombinasi keduanya, yang masing-masing membantu menemukan titik perpotongan dua garis sebagai solusi. Pemahaman SPLDV penting karena aplikasinya dalam kehidupan sehari-hari, seperti menyelesaikan masalah keuangan, perencanaan, atau distribusi, serta melatih keterampilan berpikir logis dan analitis dalam memecahkan masalah.[/justify][b][br]D. Materi[/b][br][justify]Sistem persamaan linear dua variabel terdiri atas dua persamaan linear yang masing-masing bervariabel dua (misal x dan y). Dengan demikian, bentuk umum dari Sistem Persamaan Linear Dua Variabel dapat kita tuliskan sebagai berikut.[/justify][table][tr][td]ax + by = c[/td][td] atau [/td][td]px + qy = r[/td][/tr][tr][td]dll.[/td][td][br][/td][/tr][/table][justify]Suatu persamaan dikatakan sistem persamaan linear dua variabel apabila memiliki karakteristik yaitu :[br][/justify][list=1][*]Menggunakan relasi tanda sama dengan (=)[/*][*]Memiliki dua variabel[/*][*]Kedua variabel tersebut memiliki derajat satu atau berpangkat satu[/*][/list][justify][br]Untuk menyelesaikan cara menghitung spldv (sistem persamaan linier dua variabel) maka dapat diselesaikan dengan 4 metode berikut ini :[br][b]Metode Substitusi[/b][br]Cara menyelesaikan SPLDV dengan mengganti salah satu peubah atau variabelnya.[br][b]Metode Eliminasi [/b][br]Cara untuk menyelesaikan sistem persamaan linier dua variabel dengan cara mengeliminasi atau menghilangkan salah satu variabel dengan menyamakan koefisien dari persamaan tersebut.[br][b]Metode Gabungan (Subsitusi dan Eliminasi)[/b][br]Cara atau metode untuk menyelesaikan suatu persamaan linier dengan mengunakan dua metode yaitu metode eliminasi dan substitusi secara bersamaan.[br][b]Metode Grafik[/b][br]Metode sistem persamaan linear dua variabel yang ke-empat ini adalah metode grafik.[/justify][b][br]D. Latihan Soal[br][/b][list=1][*]Tentukan himpunan penyelesaian dari persamaan berikut ini x + 3y = 15 dan 3x + 6y = 30.[/*][*]Tentukan himpunan penyelesaian dari persamaan 3x + 5y = 16 dan 4x + y = 10.[/*][*]Tentukan himpunan penyelesaian dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8. [/*][*]Tentukan himpunan penyelesaian dari sistem persamaan berikut ini 2x – 3y = 7 dan 3x + 2y = 4.[/*][*]Tentukan himpunan penyelesaian dari sistem persamaan berikut ini 2x + y = 4 dan x - 2y = -3[/*][/list]
LKPD SPLDV
Sistem Persamaan Linear Variabel
Sistem Persamaan Linear dan Dua Variabel (SPLDV) adalah kumpulan[br]dua atau lebih persamaan linear dalam dua variabel, yaitu x dan y. Dalam SPLDV,[br]tujuan utama adalah menemukan nilai-nilai x dan y yang memenuhi semua persamaan[br]tersebut secara bersamaan. SPLDV biasanya diajarkan dalam matematika sebagai[br]dasar untuk pemahaman konsep persamaan linear dan sistem persamaan.[br][br]