解の公式は分解と不変化から
[b][size=150]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][/size][/b][br]2次方程式の解の公式を導くためには、[b]平方完成[/b]をするのが普通です。[br]また、[b]因数定理[/b]や多項式の[b]係数分離の割り算(組み立て除法)[/b]などを使えば、[br]解の公式も平方完成も使わずに、[b]次元下げ[/b]ができます。[br][b]数値方程式[/b]ならその方針はとても重要です。[br][br]でも、[b]係数が数値ではない文字だけの一般方程式[/b]の解の公式を作るときは、[br]方針を変える必要があります。[br]一般方程式の解の公式を作る鍵は[size=150][color=#0000ff][b]分解[/b]にある。[br][br][/color][/size]手始めに、2次方程式の解の公式を作ってみよう。[br][br][b][size=150]<2次方程式>[br][br][/size][/b]解の公式を作るための土台[br]・2次式で対称式×交代式に因数分解できるものがある。[b]x[sup]2[/sup]-y[sup]2[/sup]=(x+y)(x-y)[/b][br]・[b][color=#0000ff]連立方程式 [/color][/b]x+y=p, x-y=qからx=(p+q)/2、y=(p-q)/2[br][br](ゴール地点)解の公式[br] モニック(最高次の係数が1)な2次方程式[b]f(x)=x[sup]2[/sup]-ax+b=0の[/b][b]解の公式は[br] x=(α,β)=(a±√D)/2 (D=a[sup]2[/sup]-4b)[/b][br][br](スタート地点)ガロア理論[br]2次方程式のf(x)=x[sup]2[/sup]-ax+b=0の基礎体をF=Qとして、f(x)の[b]最小分解体をE=Q(α,β)[/b]とする。[br]Eの[b]ガロア群Gの位数は2!=2で2は素数だから、Gは恒等置換と互換の2要素{e,ρ=(1 2)}の巡回群だ。[/b][br][br](途中経過)[br]f(x)=0の2つの解をα、βとして、p=α+β, [b][color=#0000ff]q=α-β[/color][/b]とする。2次式の因数分解からの発想だ。[br]この2式で解のかき混ぜをGの[b][color=#0000ff]ρ(ロー)[/color][/b]でやってみよう。ρ(α)=βのように、2解は交換される。[br]・pは対称式なのでαとβを入れ替えても和pは同じだから、そのままでρで不変だね。[br]・[b]qは対称式ではない[/b]からくずれる。これを不変化したい。ρ(q)=(-1)q。[br] 2回ρをすると、ρρ(q)=qになりもどる。[br] そこで、[b]2回ρする代わりに、qを2回転、つまり、2乗してみる[/b]。[br] q[sup]2[/sup]=(α-β)[sup]2[/sup]=(α+β)[sup]2[/sup]-4αβなら、ρのかきまぜで不変化できた。だから、[b]q∈E、q[sup]2[/sup]∈F[/b]となる。[br][b][color=#0000ff] q[sup]2[/sup]は有理数であり、解と係数の関係から係数表示ができるし、qは最小分解体、解が出せる体にある。[br][/color][/b][color=#0000ff]・つまり、[b]qがあると解を表現できる、解の公式が作れる[/b]ということだね。[br][/color](このq[sup]2[/sup]を判別式Dと名付けることが多いですね。)[br]あとは、計算問題だ。D=q[sup]2[/sup]=(α-β)[sup]2[/sup]=(α+β)[sup]2[/sup]-4αβ=a[sup]2[/sup]-4bとなる。[br]連立方程式α+β=a, α-β=±√Dを解いて、x=(p+q)/2、y=(p-q)/2[br]体の視点で見ると、Eは√Dを添付した[b]拡大体F(√D)[/b]ということだね。
α,βをスローに置換してみる
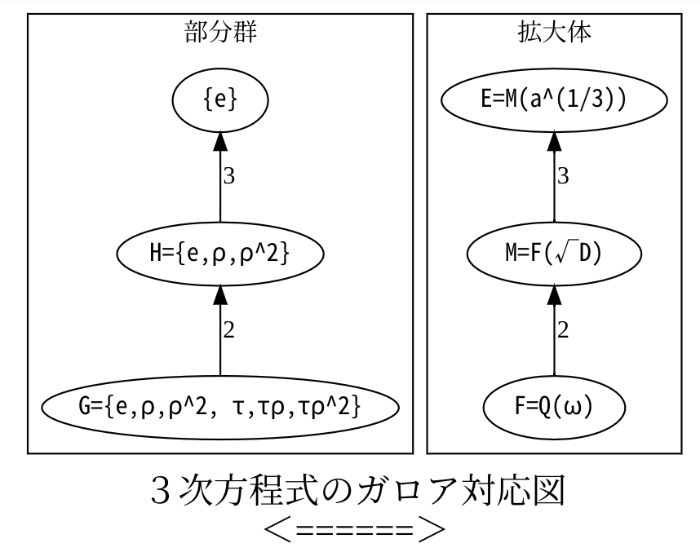
1.3次方程式の解の公式
[size=150][b][size=150]<スタートとゴールの確認>[br][/size][/b][size=100]さっきの2次方程式のときと同じ流れで取り組んでみよう。[br]・3次式が1の3乗根で1次式の積に分解できる[b][color=#0000ff]。[/color][/b][math]x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x+\omega y+\omega^2z\right)\left(x+\omega^2y+\omega z\right)[/math] [br]・3!=3*2*1=3*2は3[b][color=#0000ff]の階乗の素因数分解[/color][/b]だ。[br]・一番カンタンな3次方程式x[sup]3[/sup]=1の解はx=1,ω,ω[sup]2[/sup]で、ω[sup]2[/sup]+ω+1=0で、ω=(-1+√3i)/2[br] 表記をカンタンにするためだけにω[sup]2[/sup]=δとする。δω=1,1+ω+δ=0となるね。[br]・[b][color=#0000ff]連立方程式 [/color][/b]x+y+z=0, x+ωy+δz=r, x+δy+ωz=sを解くと、x=(0+r+s)/3,y=(0+ωr+δs)/3,z=(0+δ[sup][/sup]r+ωs)/3[br]この4つの基本から3次方程式の解の公式が作れるでしょう。[br][br](ゴール地点)[size=150][size=100]カルダノの公式(手順)[br][/size][/size]3次方程式 [math]X^3+pX+q=0[/math]から、[br][math]t^2+qt-\left(\frac{p}{3}\right)^3=0[/math] を作り、[/size][size=100]2つの解α,βの3乗根 [/size][size=100][math]r,s[/math]から、3次方程式の解は[math]X=r+s,\omega r+\omega^2s,\omega^2r+\omega s[/math] [br]または、[br][b][color=#0000ff][size=150][math]t^2+27qt-27p^3=0[/math][/size][/color][/b][/size][size=100]を作り、2つの解α,βの3乗根 [math]r,s[/math]から、X=[math]\frac{1}{3}(r+s),\frac{1}{3}(ωr+ω^2s),\frac{1}{3}(ω^2r+ωs)[/math] 。[/size][size=100][br](スタート地点)ガロア理論[br]3次方程式の[math]f(x)=X^3+pX+q=0[/math]の3つの解をx,y,zとする。[br][b] 基礎体はωが自由につかえるようにQにつけてF=Q(ω)。[br][/b][b]最小分解体をE=Q(x,y,z)[/b]とする。解と係数の関係からxyz=-q, xy+xz+zx=p, x+y+z=0。[br]Eの[b]ガロア群Gの位数は3!=3*2[/b]だからG=S3=C3×C2だ。S3は可解で正規列が[b]S3▷A3▷{1}となるね。[/b][br]S3の生成元を3次の巡回置換ρ=(1 2 3), 互換τ=(1 2)とすると、ガロア群G=<ρ,τ>={e, ρ,ρ[sup]2[/sup], τ,τρ, τρ[sup]2[/sup]}。[br][b][color=#0000ff]Gの正規部分群は、H={e, ρ, ρ[sup]2[/sup]}=A3交代群で3解(正三角形の3頂点)をぐるぐる回転する巡回群。[br]G/H=<ρ,τ>/[b][color=#0000ff]<ρ>=<[b][color=#0000ff]τ>=[/color][/b][/color][/b]{e,τ}は正三角形を裏返すかどうかの巡回群。[br][br][/color][/b][/size][/size][b][size=150]<正規部分群Hに対する中間体Mを作るための見通しをたてる>[br][/size][/b][size=150][size=100]群Hで動かない中間体H¥=Mは何でしょうか?[/size][/size][br][b][color=#0000ff]G/Hの剰余類群は{0,1}の剰余群,巡回群と同型なので回転を止めれば、裏表の操作だけになるね。[br]h0,h1の2種で代表させます。[br][/color]中間体Mの要素でFにない元をm,nについて[/b]h1(m)=nとする。2式p=n+m, q=n-mにh1を作用させよう。[br]2次方程式のときと同様にh1(p)は不変で、h1(q)は符号が反転する。[br]だから、p=[b]n+m=F数、q=n-m≠F数。[/b][br]h1((m-n)[sup]2[/sup])=h1(m-n)h1(m-n)=(n-m)(n-m)=[b](n-m)[sup]2[/sup]∈F[/b]です。qが2乗で不変化できた。[br]これから、q=[b]m-n=√F数[/b]となり、[b]m,nの和と差からm=(√F数+F数)/2[/b]となるね。[br]だから、[b]M=F(√F)[/b]。[b][color=#0000ff]中間体MはFの平方根をFに添付した拡大体になるということだね。[br][/color][/b][br]このあとは、[br]3つの解x,y,z∈Eに対して、0=x+y+z, r=x+ωy+δz, s=x+δy+ωzとして、[br]x=(0+r+s)/3,y=(0+ωr+ω[sup]2[/sup]s)/3,z=(0+ω[sup]2[/sup]r+ωs)/3[br]r,sをf(x)=0の係数p,qで表すことで、[b]解の公式ができるはずだ[/b]。

α,βの3乗根u,vを組み合わせて3つの解を作る
[size=150][b]<Fに平方根√Dを添付してMを作る>[br][/b][/size][b][color=#0000ff]正規部分群Hにあるかきまぜρで不変な式を作りましょう。[br]X[sup]3[/sup]+pX+q=0の3つの解をx,y,zとするとき、因数分解の式から3式を作ろう。[br][/color][/b][size=150][b][color=#0000ff]0=x+y+z, [br]r=x+ωy+δz, [br]s=x+δy+ωz[/color][/b] [br][/size]このうちの2式[b]r,s[/b]に[b]巡回ρ[/b]をしかけたときの変化から、不変化する式を作ろう。[br]( 表記のカンタンのためにω[sup]2[/sup]=δとする。[b]δ+ω= -1, δω=1。[/b] 解と係数の関係から、[br] xyz=-q, xy+yz+zx=p, [b]x+y+z=0[/b]となり、[b]y+z=-x[/b], [b]x[sup]3[/sup]=-px-q[/b], y[sup]3[/sup]=-py-q, z[sup]3[/sup]=-pz-q などを使おう)[br][b][color=#0000ff][br]rs[/color][/b] = (x+ωy+δz)(x+δy+ωz)=x[sup]2[/sup]+y[sup]2[/sup]+z[sup]2[/sup]+(δ+ω)(xy+yz+zx)=(x+y+z)[sup]2[/sup]-2(xy+yz+zx)-(xy+yz+zx)=[b] [color=#0000ff]-3p[/color][br][color=#0000ff]r+s[/color] [/b]= x+ωy+δz+x+δy+ωz=2x+(ω+δ)(y+z)=2x+x=[b][color=#0000ff]3x[/color][/b][br][b][color=#0000ff]ρ[/color][/b](r)=y+ωz+δx=δ(x+ωy+δz)=[color=#0000ff][b]δ[/b][/color]r, [br][b][color=#0000ff]ρ[/color][/b](s)=y+δz+ωx=ω(x+δy+ωz)=[color=#0000ff][b]ω[/b][/color]s。[br]3回ρをすると、ρρρ(r)=δ[sup]3[/sup]r=r、ρρρ(s)=ω[sup]3[/sup]s=sになりもどる。[br]そこで、3[b]回ρする代わりに、r,sを3回転、つまり3乗してみる[/b]。[br][b]ρ(r[sup]3[/sup])=(ρ(r))[sup]3[/sup]=(δr)[sup]3[/sup]=r[sup]3[/sup]、ρ(s[sup]3[/sup])=(ρ(s))[sup]3[/sup]=(ωs)[sup]3[/sup]=s[sup]3[/sup][br]正規部分群Hのかきまぜρ[/b]でr[sup]3[/sup],s[sup]3[/sup]ともに不変だから、r[sup]3[/sup]+s[sup]3[/sup]も不変で[b]中間体M[/b]にある。[br]不変化が成功したね。あとはこの不変式を係数表示にすればいいね。[br][br][b][color=#0000ff]ρ(r[sup]3[/sup]+s[sup]3[/sup])[/color][/b]=r[sup]3[/sup]+s[sup]3[/sup]=(r+s)[sup]3[/sup]-3rs(r+s)=(3x)[sup]3[/sup]-3([b]-3p[/b])(3x)=27[b]x[sup]3[/sup][/b]+27px=27([b]-px-q[/b]+px)=[color=#0000ff][b]-27q[/b][/color][br][b][size=150][color=#0000ff]r[sup]3[/sup]+s[sup]3[/sup]=-27q, r[sup]3[/sup]s[sup]3[/sup]=-27p[sup]3[br][/sup][/color][/size][sup][/sup][/b]r[sup]3[/sup],s[sup]3[/sup]は[b][color=#0000ff][size=150]t[sup]2[/sup]+27qt-27p[sup]3[/sup]=0[/size][/color][/b]の解ですね。(補助方程式)[br][math]D=q^227^2+4\cdot27p^3=(2\cdot27)^2(\left(\frac{q}{2}\right)^2+\left(\frac{p}{3}\right)^3)[/math][br][b]M=F(√D)にFを拡大できました[/b]。[br][br][b][size=150]<Mに3乗根a[sup]1/3[/sup]を添付してEを作る>[br][/size][/b][math]r^3,s^3=\frac{\left(-27q\pm2\cdot27\sqrt{\left(\frac{q}{2}\right)^2+\left(\frac{p}{3}\right)^3}\right)}{2}=-27\left(\frac{q}{2}\mp\sqrt{\left(\frac{q}{2}\right)^2+\left(\frac{p}{3}\right)^3}\right)[/math][br] r,s =[math]-3\sqrt[3]{\frac{q}{2}\pm\sqrt{\left(\frac{q}{2}\right)^2+\left(\frac{p}{3}\right)^3}}[/math] [br][br]3つの解x,y,z∈Eに対して、0=x+y+z, r=x+ωy+δz, s=x+δy+ωzとして、[br]連立方程式を解いた式、[br]x=(r+s)/3,[br]y=(ωr+ω[sup]2[/sup]s)/3,[br]z=(ω[sup]2[/sup]r+ωs)/3[br]これで、ゴールですね。[br][br][color=#9900ff][b][u][size=150]質問:3次方程式の解の公式をgeogebraで視覚化するにはどうしたらよいでしょうか。[br][/size][/u][/b][/color]まず2次方程式x2+ax+b=0の解の公式を作りましょう。[br]3次方程式のカンタン形のx3+px+q=0を作り、a=q, b=-(p/3)^3の数式を書きます。[br]p, qはスライダーで整数の可変値にします。[br]2次方程式の解α、βにしたときにその3乗根の出し方は注意が必要です。[br]z=α,βを複素数として設定した場合、その3乗根cbrt(z)が予想と違うことがおきます。[br]z=α,βの虚部が正ならば、3乗根は正しく出せますが、[br]zの虚部が0で実部が負の数のときは、ただの3乗根関数cbrt(z)が複素数になってしまいます。[br]偏角が3分の1になり、大きさが3乗根になるからです。[br]それの防ぎ方は、zの虚部imaginary(z)==0なら、実部real(z)だけを3乗根関数cbrt()に入れましょう。
次は4次方程式の解の公式とガロア理論をつなげたい。[br]その前にまとめをしておこう。[br][br][b]<解の公式があることの一般化>[/b][br]F上のn次の一般代数方程式が代数的に解けるのは、[b]代数的解法[/b](Fに四則演算とべき根を有限回を行って、解が表現できる)があること。[br]・体で見ると、体Fから拡大を繰り返した先に最小分解体Eに到達する[color=#0000ff][b]べき根拡大の連続[/b][/color]になるね。[br]・群で見ると、ガロア群Gal(E/F)=Snの[b][color=#0000ff]正規分群がH1,H2,...,{1}まで続き[/color][/b]、[br] 商群の位数が巡回群となるときは可解群となることだ。[br] 商群の位数がmならば、m乗根を体に添付して拡大する。[br](可解群の商群が「巡回群」を「[b]アーベル群[/b]」、「[b]素数位数の群[/b]」としても同じこと)[br][color=#0000ff][b]・つまり、商群が巡回群なら、ぐるぐる回してぜんぶの要素が作れる。[br] ぐるぐる回すかわりにべき乗して不変化すれば、固定体に属する要素が作れる。[br] 不変化式を係数で表すと、解の公式につながる。[br][/b][/color]・n次方程式のがロア群の商群作りはn!の素因数分解による。
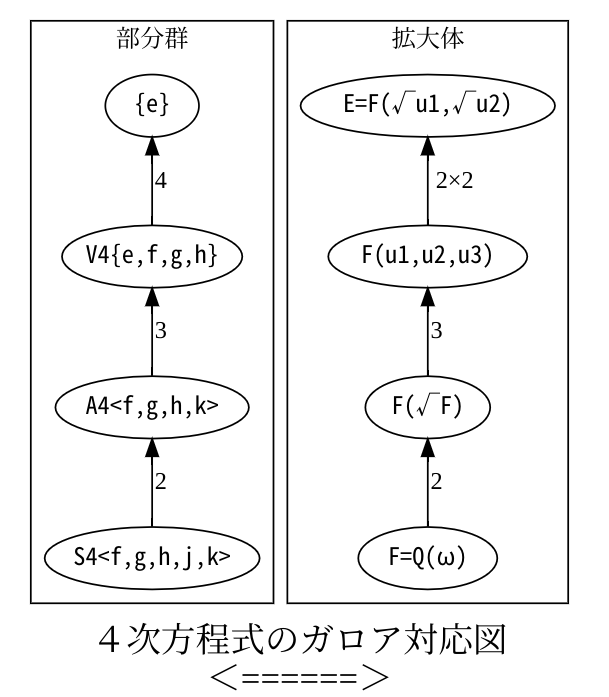
2.4次方程式の解の公式
[b]<スタートとゴールの確認>[br][/b][size=100]さっきの3次方程式のときと同じ流れで取り組んでみよう。[br]4次式で1次式の積に分解できるものがある。[br]・ [math]x^4-2\left(s^2+t^2+u^2\right)x^2-8stux+\left(s^2+t^2+u^2\right)^2-4\left(s^2t^2+t^2u^2+u^2s^2\right)[/math][br] [math]=\left(x-s-t-u\right)\left(x+s+t-u\right)\left(x+s-t+u\right)\left(x-s+t+u\right)[/math] [br]4!=4*3*2*1=3*2*2*2[br][br](ゴール地点) オイラーの方法[br] ・ [math]x^4+px^2+qx+r=0[/math]と因数分解・ [math]x^4-2\left(s^2+t^2+u^2\right)x^2-8stux+\left(s^2+t^2+u^2\right)^2-4\left(s^2t^2+t^2u^2+u^2s^2\right)[/math][br] [math]=\left(x-s-t-u\right)\left(x+s+t-u\right)\left(x+s-t+u\right)\left(x-s+t+u\right)[/math] [br]を比較して、[b]p=-2(s[sup]2[/sup]+t[sup]2[/sup]+u[sup]2[/sup])、q=-8stu、r=(p/2)[sup]2[/sup]-4(s[sup]2[/sup]t[sup]2[/sup]+t[sup]2[/sup]u[sup]2[/sup]+u[sup]2[/sup]s[sup]2[/sup])[br]a=4s[sup]2[/sup], b=4t[sup]2[/sup],c=4u[sup]2[/sup][/b]とおくと、a+b+c=-2p、abc=q[sup]2[/sup]、4r=p[sup]2[/sup]-(ab+bc+ca)から、 [/size][size=100][math]t^3+2pz^2+\left(p^2-4r\right)t-q^2=0[/math] (補助方程式)を作る。[br][b]3つの解t=a,b,cから、4で割って平方根をとり、s,t,uに戻すと[br][/b][b] [math]8stu=q,s=\sqrt{\frac{a}{4}},t=\sqrt{\frac{b}{4}},u=\sqrt{\frac{c}{4}}[/math] となる。[b]4次方程式の解は[math]x=s+t+u,s-t-u,-s+t-u,-s-t+u[/math] [br][/b][/b][br][/size][size=100](スタート地点)ガロア理論[br]4次方程式の[math]f(x)=X^4+pX^2+qX+r=0[/math][br][b]基礎体はωが自由につかえるようにQにつけといたほうがよい。基礎体F=Q(ω)。[br][/b][b]最小分解体をE[/b]とする。4つの解を[b]α,β,γ,δ[/b]とすると、 解と係数の関係から[br][b][color=#0000ff]α+β+γ+δ=0, [br]αβ+αγ+αδ+βγ+βδ+γδ=p,[br]αβγ+αβδ+αγδ+βγδ=-q,[br]αβγδ=r[/color][/b][br]Eの[b]ガロア群Gの位数は4!=3*2*2*2[/b]だからG=S4=C3×C2×V4だ。[br]S4は可解で[b]S4▷A4▷V4▷C2▷{1}[/b][br][color=#0000ff][b]対称群S4は4本あみだで、正六面体P6の自己同型作用と同型だね。[/b][br]生成元は5つ。[b]f=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3)、j[b]=(3 4)、k[b]=(2 4 3)[br][/b][/b][/b][/color]ア・4次巡回置換は3×2×1=6個。(1 2 3 4),(1 2 4 3),(1 3 2 4),(1 3 4 2),(1 4 2 3),(1 4 3 2)[br] 互換が2つなら共通要素がない積で4-1=3個。f[b]=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3) [/b](→偶置換)[br]イ・互換が1つなら4C2=6個。(1 2),(1 3),(1 4),(2 3),(2 4),[b]j=(3 4)[/b]だね。[br]ウ。互換が2つで1つは不変な3次巡回置換は4×2=8個。(→偶置換)[br] (1 2 3),(1 3 2), (1 2 4),(1 4 2), (1 3 4),(1 4 3), (2 3 4),[b]k=(2 4 3)[/b] [br]エ・互換の数が0ならeの1個。(→偶置換)[br]P6の作用[br]ア・2対面の中心を結ぶ6÷2=3軸で90度の1、2、3倍回転する、3×3=9個。[br]イ・対辺の中点どうしを結ぶ4×3÷2=6軸での180度回転で6個。[br] 2対辺を含む平面内の2対角線が交換されるが、残りの対角線は上下反転するが自分と重なる。[br]ウ・主対角線、4軸での120度の1、2倍回転する、4×2=8個。[br]S4の可解列[br][b]V4 = <f、g、h>={e,f,g,h}[br]A4 = <f、g、h、k>={e,f,g,h}+{e,f,g,h}k+{e,f,g,h}k[sup]2[/sup][br][/b][/size][size=150][size=100][b]W1 = <f>=[/b][b]{e,f}, W2=<g>={e,g}, W3 = <h>={e,h}[/b][/size][/size]
[size=150][b]<中間体を作る>[br][/b][/size]商群の指数はS4/A4=24/12=2、A4/V4=12/4=3、V4/{1}=4[br][b]指数が3の拡大があるので、3次方程式の解の入れ替えにそなえ[/b]基礎体を[b]F=Q(ω)[/b]とする。[br][b]・群A4に対する中間体はKは、S4/A4=2だから2次拡大。[/b]S4/A4={e,f} = C2 3次方程式のときと同様に√Fの数をFに添付する。群A4に対応する中間体は[b]K=F(√F)[/b][br][b]・群V4に対応する中間体は、A4/V4=3だから3次拡大だね。[/b]A4/V4={e,k,k[sup]2[/sup]} = C3[br] f(x)=0の4つの解[b]α,β,γ,δ[/b]でつくる3つの式u1,u2,u3でV4の作用fで不変な要素を作ろう。[br] V4 = <f=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3)>={e,f,g,h}[br][color=#0000ff][b] u1=(α+β)(γ+δ), u2=(α+[color=#0000ff]γ)([/color]β+δ), u3=(α+[color=#0000ff]δ)([/color]β+γ) とおくと、[br][/b][/color][b] f[/b](u1)=u1, [br][b][b][b] f[/b][/b][/b](u2)=u2, [br][b][b] f[/b][/b](u3)=u3,......のようにして、[br] u1,u2,u3はV4の不変だから、V4に対応する中間体は[b]M=K(u1,u2,u3) 解と係数の関係を満たす3次方程式を作ろう。[/b][size=100]詳しい計算は省略。。。。[/size][b][br]ここで(t-u1)(t-u2)(t-u2)=[/b][math]t^3-2pz^2+\left(p^2-4r\right)t+q^2=0[/math][b] [br]u1+u2+u3[/b][b]=-2p[br]u1u2+u2u3+u3u1=p[sup]2[/sup]-4r[br]u1u2u3=q[sup]2[/sup][/b][b][br]これで、t=u1,u2,u3が求められる。[br][br]・いよいよ、最後の拡大に入る。[b]W1 = <f>=[/b][b]{e,f}, W2=<g>={e,g}, W3 = <h>={e,h}[/b][br] 群W1,W2,W3に対応する中間体は、V4/Wi=2だから2次拡大だね。[br][/b] Wiに対応する中間体はu1,u2,u3の平方根をMに添付して、[b]M(√u1),[/b][b]M(√u2),[/b][b]M(√u3)の3系統の拡大体。[br] さらに、それらをすべて含むのがゴールの最小分解体[/b][b]N=M(√u1,√u2,√u3)[br][/b][br]連立方程式[b]u1=(α+β)(γ+δ), u2=(α+γ)(β+δ), u3=(α+δ)(β+γ) を解こう。[br][b][b][color=#0000ff][b]α+β+γ+δ=0と[/b][/color][/b][/b][/b]解と係数の関係から、[br][b]α+β[/b], [b]γ+δ[/b]は([b]α+β)+[/b]([b]γ+δ)=0,([/b][b]α+β)([/b][b]γ+δ)=u1[/b][color=#0000ff][b]から、[/b][/color]x[sup]2[/sup]=u1の解、[br][b]α+γ[/b], [b]β+δ[/b]は([b]α+γ)+[/b]([b]β+δ)=0,([/b][b]α+γ)([/b][b]β+δ)=u2から、[/b]x[sup]2[/sup]=u2の解、[br][b]α+δ,β+γ[/b]は([b]α+δ)+(β+γ)=0,([/b][b]α+δ)(β+γ)=u3から、[/b]x[sup]2[/sup]=u3の解 。[br]だから、[b]α+β[/b], [b]γ+δ[/b]=√u1, -√u1、[b]α+γ[/b], [b]β+δ[/b]=√u2, -√u2、[b]α+γ[/b], [b]β+δ[/b]=√u3, -√u3[br][color=#0000ff]実際は、[b]u1u2u3=q[sup]2[/sup][/b] [b]解と係数の関係が使える。u1,u2から、√u3は決まるので、N=M(√u1,√u2,√u3)=M(√u1,√u2)[br]連立方程式を解けば、[br]α[/b]=(√u1+√u2+√u3-(-√u1-√u2-√u3)/2)/3=( √u1+√u2+√u3)/2[br][b]β[/b]=√u1-(√u1+√u2+√u3)/2=( √u1-√u2-√u3)/2[br][b]γ[/b]=√u2-(√u1+√u2+√u3)/2=(-√u1+√u2-√u3)/2[br][b]δ[/b]=√u3-(√u1+√u2+√u3)/2=( √u1-√u2+√u3)/2[br][/color]最後の拡大はV4の拡大だれど、4=2×2より、3次方程式の3つの解u1,u2,u3[br]から適当に2つ選び、それぞれの解√ui, √ujを添付する拡大だから、2次拡大を独立に2つ行うことになる。だから4は素数ではないが、素数2の拡大を別々に2つやることになる。[br]拡大次数はM=K(u1,u2,u3)に対して、2×2=4であって、N=M(√ui, √uj)ということだね。