Kinematics of Linear Motion
This GeoGebra book covers Chapter 8: Kinematics of Linear Motion based on the Form 5 Additional Mathematics syllabus. It includes mind maps, formulas, interactive graphs, and Augmented Reality applications to help students visualize and understand linear motion concepts such as displacement, velocity, acceleration, and equations of motion.
Table of Contents
- Introduction
- Introduction
- Kinematic Linear Motion Mind Map
- Formulas List
- Application of AR in Kinematic Linear Motion
- 8.1 Displacement, Velocity, and Acceleration as Function of Time
- 8.1 Displacement, Velocity, and Acceleration as Functions of Time
- Example 2
- Example 3
- Self Exercise 8.1 Question 1
- Self Exercise 8.1 Question 2
- Formative Exercise 8.1 Question 2
- Formative Exercise 8.1 Question 3
- Formative Exercise 8.1 Question 5
- 8.2 Differentiation in Kinematics of Linear Motion
- 8.2 Differentiation in Kinematics of Linear Motion
- Example 6
- Example 7
- Example 10
- Self Exercise 8.4 Question 2
- Formative Exercise 8.2 Question 1
- Formative Exercise 8.2 Question 2
- Formative Exercise 8.2 Question 3
- Tik Tok AR Filter
- 8.3 Integration in Kinematics of Linear Motion
- 8.3 INTEGRATION IN KINEMATICS OF LINEAR MOTION
- Example 11
- Example 12
- Self Exercise 8.6 Question 1
- Self Exercise 8.6 Question 2
- Self Exercise 8.6 Question 3
- Self Exercise 8.6 Question 4
- Self Exercise 8.7 Question 1
- Self Exercise 8.7 Question 2
- Self Exercise 8.7 Question 3
- Self Exercise 8.7 Question 4
- 8.4 Application of Kinematics of Linear Motion
- 8.4 Application of Kinematics in Linear Motion
- Example 1
- Example 2
- Self Exercise 8.8 Question 1
- Self Exercise 8.8 Question 2
- Self Exercise 8.8 Question 3
- Self Exercise 8.8 Question 4
- Summative Exercise
- Question 1
- Question 2
- Question 3
- Question 4
- Question 5
- Question 6
- Question 7
- Question 8
- Question 9
- Question 10
- Question 11
- Question 12
- Question 13
- Question 14
- SPM Questions Collection
- 2020 Penang
- 2022 Pahang
- Past Year Perak
- 2023 Melaka
- 2024 SPM Trial Negeri Sembilan(Paper 2)
- Trial SPM Negeri Sembilan 2023
- Trial SPM Pahang 2023
- GeoGebra Visualizations
- INTERACTIVE GAME
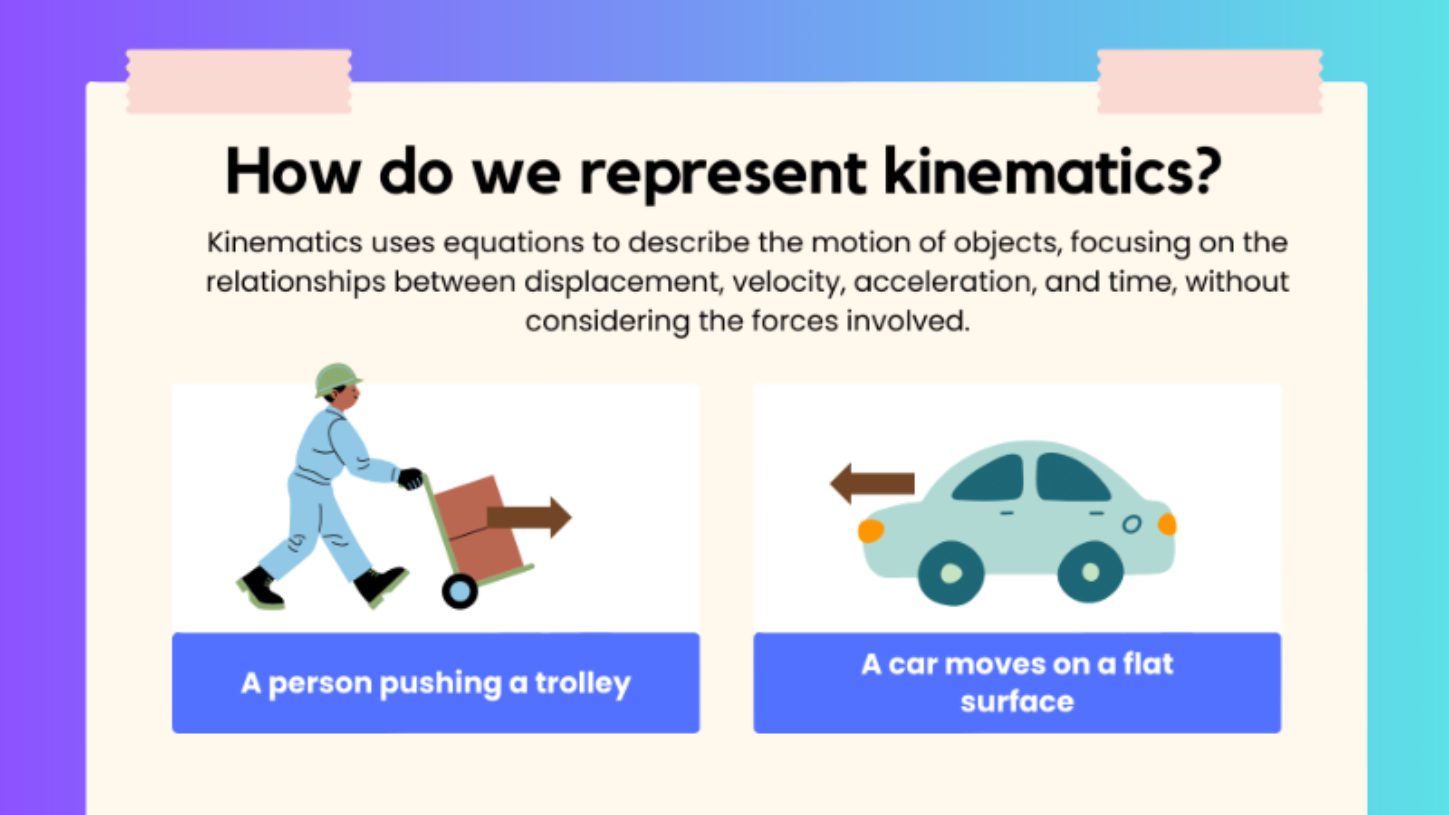
Introduction
[b][size=150][size=200][color=#0000ff]What is Linear Kinematic Motion?[/color][/size][/size][/b][size=100][justify][size=150]Linear kinematic motion refers to the study of the [i]movement of objects along a straight line[/i], describing how their position, velocity, and acceleration change over time. This concept is fundamental in understanding motion in physics and is widely applied in various real-world situations, such as driving a car, objects falling freely under gravity, or the motion of projectiles.[/size][br][br][size=150][/size][size=150]Kinematics focuses on describing the motion of an object without considering the forces that cause it. In linear motion, we are particularly interested in how the following quantities interact:[br][/size][/justify][list=1][*][size=200][size=150][b][i]Displacement (s):[/i][/b] The distance and direction of an object's movement from its initial position.[/size][/size][/*][*][size=200][size=150][b][i]Velocity (v):[/i][/b] The speed of the object in a specific direction. It can be initial velocity (u) or final velocity (v).[/size][/size][/*][*][size=200][size=150][b][i]Acceleration (a):[/i][/b] The rate at which the velocity changes over time.[/size][/size][/*][*][size=200][size=150][b][i]Time (t):[/i][/b] The duration of the motion.[br][/size][/size][/*][/list][/size]
8.1 Displacement, Velocity, and Acceleration as Functions of Time
[size=200][b][color=#0000ff]What is displacement?[br][/color][/b][/size][br][size=150][b]Displacement (s)[/b] of a particle and a fixed point is the distance between the particle and the nearest fixed point measured in a certain direction.[br][/size][i][color=#1e84cc][size=150][b]Here is a simpler and easier to understand way to explain the displacement, velocity and acceleration based on the direction of motion of the particle relative to the fixed point O: [/b][/size][/color][/i][size=150][color=#ff0000][b]Displacement:[/b][br][/color][/size][size=150][list][*][size=150][b]Negative displacement[b] (s<0)[/b]: The particle is to the left of point O.[/b][/size][/*][/list][list][*][size=150][b]Zero displacement[b] (s=0): The particle is exactly at point O.[/b][/b][/size][/*][/list][list][*][size=150][b]Positive displacement (s>0): The particle is to the right of point O.[/b][br][/size][/*][/list][/size][justify][color=#ff0000][b][/b][size=150][b]Velocity:[/b][br][/size][/color][/justify][size=150][i][list][*][size=150][b]Negative velocity[b] (v<0)[/b]: The particle moves to the left.[/b][/size][/*][/list][list][*][size=150][b]Zero [b]velocity [/b][b](v=0): The particle remain still.[/b][/b][/size][/*][/list][list][*][size=150][b]Positive velocity (v>0): [b]The particle moves to the right.[/b][/b][br][/size][/*][/list][/i][/size][size=150][color=#ff0000][b]Acceleration:[/b][/color][/size][i][list][*][b][size=150]Negative acceleration[b] (a<0)[/b]: The particle's velocity is [b]increasing[/b] over time (the particle is speeding up).[/size][/b][/*][/list][size=150][list][*][b]Zero [b]acceleration[/b][b](v=0): The particle's velocity is [b]constant[/b] (either at its maximum or minimum).[/b][/b][/*][/list][/size][/i][i][size=150][list][*][i][size=150][b]Positive acceleration[b] (a>0)[/b]: The particle's velocity is [b]decreasing[/b] over time (the particle is slowing down). [/b][/size][/i][/*][/list][/size][/i]
8.2 Differentiation in Kinematics of Linear Motion
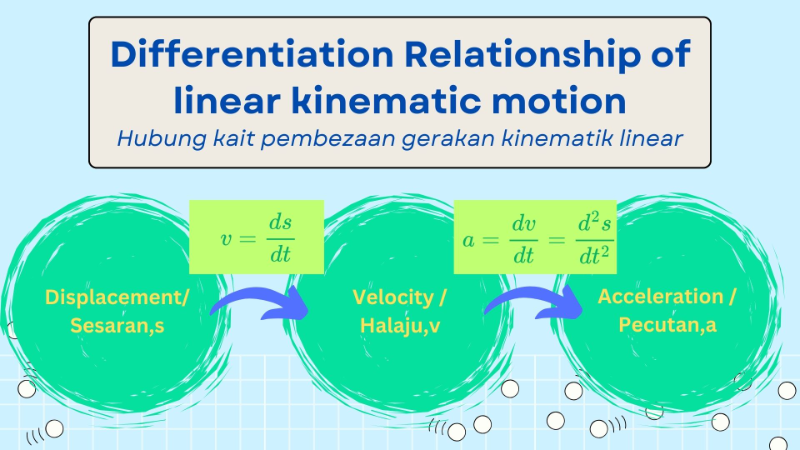
[justify][size=100]Differentiation in linear kinetic motion refers to the mathematical process of determining the rate of change of motion-related quantities, such as displacement, velocity, and acceleration, with respect to time. These rates are foundational in understanding the dynamics of objects in linear motion.[b] The differentiation always starts from displacement, s=f(x). [br][/b][/size][i][size=100][br][/size][/i]The [b]velocity[/b] is defined as [b]the rate of change of displacement with respect to time[/b]. Hence, the velocity function,v is given by:[br][/justify][center][br][math]v=\frac{ds}{dt}[/math][br][br][/center][justify][size=100]The[b] acceleration[/b] is [b]the rate of change of velocity with respect to time[/b]. Hence, the acceleration function,a is given by:[br][br][/size][/justify][i][center][math]a=\frac{dv}{dt}=\frac{d^2s}{dt^2}[/math][/center][/i][justify][br]The relationship between the displacement function, s, the velocity function, v, and the acceleration function, a, can be summarized as shown in the following diagram:[/justify]
8.3 INTEGRATION IN KINEMATICS OF LINEAR MOTION
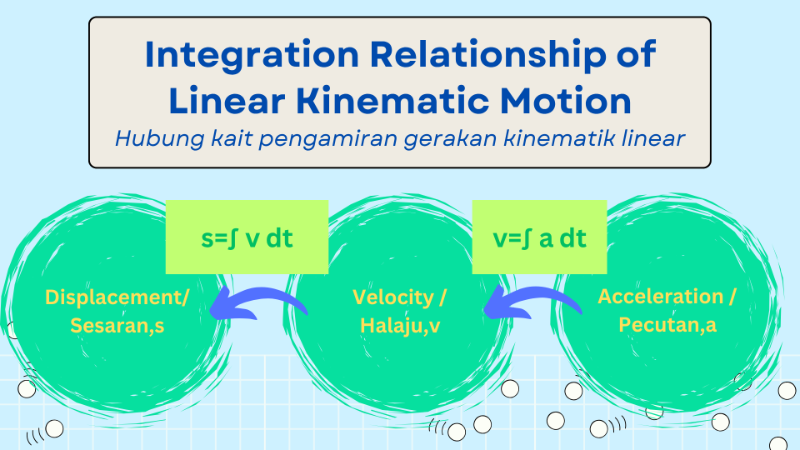
[justify]You had learnt the acceleration function, a of a particle that moves linearly can be obtained by differentiating the velocity function, v with respect to time. t, that is:[br] [math]a=\frac{dv}{dt}[/math][br][br]However, if the acceleration function, a, of a particle is given, how can we determine the velocity function,v of the particle?[br][br]When the acceleration function [math]a=\frac{dv}{dt}[/math], the velocity function, v can be determined by integrating the acceleration function, a with respect to time, t which is [math]v=\int a[/math]dt.[i][br][br][/i]In general, the relationship between acceleration function, a = h(t) and velocity function, v = g(t) can be simplified as follows:[br][/justify] [math]a=h\left(t\right)[/math] [math]\longrightarrow[/math] [math]v=\int adt[/math] [math]\longrightarrow[/math] [math]v=g\left(t\right)[/math]
[left]Given a velocity function, v, how can we determine the displacement, s, of the particle? How can we determine the velocity function, v, and alsoy the displacement function, s, of a particle from an acceleration function, a?[br][br]When the velocity function, v, is given as a function of time t, the displacement function, s, can be obtained by performing integration, which is:[br][br][br][b]s=∫ v dt[/b][br][br]and when the acceleration function, a, is given as a function of time t, the displacement function, s, can be obtained by performing two consecutive integrations, which are:[br][math]v=\int adt[/math], then follow by [math]s=\int vdt[/math][/left]
8.4 Application of Kinematics in Linear Motion
Solve linear motion kinematics problems involving differentiation and integration
We have learned that the relationship between displacement, [math]s[/math], velocity, [math]v[/math] and acceleration [math]a[/math], for an object moving linearly, is as follows.[br][br]Using differentiation[br][math]v=\frac{ds}{dt},a=\frac{dv}{dt}[/math][br][br]Using integration[br][math]v=\int a_{ }dt,s=\int v_{ }dt[/math][br][br]Many problems involving an object's linear motion can be solved with the knowledge and skills to apply this relationship.
Question 1
A particle moves along a straight line from a fixed point O. Its displacement, s metre, at t seconds after passing O is given by [math]s=2t^3-24t^2+90t[/math]. Calculate[br]
(a) the distance, in m, of the particle from the fixed point O when t=8,
(b) its velocity, in ms[sup]-1[/sup], when t=1,
(c) its acceleration, in ms[sup]-2[/sup], when t=3,
(d) the values of t, in seconds, when the particle stops momentarily.
2020 Penang
[size=150]A particle P moves along a straight line and passes through a fixed point [i]O. [/i]Its velocity, [i]v[/i] ms[sup]-1[/sup], is given by [math]v=8+2t-t^2[/math], where [i]t[/i] is the time, in seconds, after passing through [i]O.[br][Assume motion is to the right is positive.][/i][/size][br][size=150]Find[br][br](a) the initial velocity, in ms[sup]-1[/sup], of the particle,[/size]
[size=150](b) the maximum velocity, in ms[sup]-1[/sup], of the particle.[br][/size]
[size=150](c) the value of [i]t[/i] at which the particle [i]P[/i] is at instantaneous rest,[/size]
[size=150](d) the total distance, in m, travelled by particle [i]P[/i] in the first 6 seconds after passing through [i]O.[br][/i][/size]