Cup Modeling Project: Building Surfaces of Revolution

Tim Brzezinski, 7 dec, 2021

Cup Modeling Project: Building Surfaces of Revolution

Táboa de contidos

  1. your tasks
    1. Cup Modeling (1)
    2. Cup Modeling (2)
    3. Cup Modeling (3)
  2. reference
    1. Measure a Radius Accurately

1.

your tasks

  • 1. Cup Modeling (1)
  • 2. Cup Modeling (2)
  • 3. Cup Modeling (3)

1.1.

Cup Modeling (1)

Your task: Create a virtual model of this cup below. Refer to the "Measure a Radius Accurately" page to help you measure the radius of the top and bottom of this cup.
Before building in the 3D app below, you will need to measure the following:[br][list][*]Bottom radius of this cup[/*][*]Top radius of this cup[/*][*]Height of this cup[/*][/list][br]The height of this cup should be fairly easy to measure. Please refer to the [b]reference[/b] section (left) to see how to measure a radius of this cup accurately. [br]
Once you get your data, build a virtual model of this cup below. Be sure to watch the quick silent YouTube video below that illustrates how to create a surface of revolution.
How to Create a Surface of Revolution in GeoGebra 3D Calculator (quick silent demo)
Go to the [b]MENU[/b] (3 horizontal bars upper left corner). Go to [b]SAVE[/b]. Title it [b]Cup Model 1[/b]. Open this in GeoGebra 3D Calculator on you phone or tablet to test how well the virtual model fits over the real one. [br][br]If you forget how to do this, do the following: [br][list][*]Sign in to your GeoGebra account on Safari if you have an iPhone or iPad[/*][*]Sign in to your GeoGebra account on Chrome if you have an Android or other non-iOS tablet. [/*][*][url=https://youtu.be/_gjrdrqADZM?t=142]Follow the instructions seen here[/url]. (No need to watch the beginning of the video.)[/*][/list]
– Tim Brzezinski

1.2.

–

1.3.

–

2.

reference

The tasks you need to complete are located in the previous chapter. Be sure to follow the steps shown here when it comes time to to measure the bottom and top radius of a cup accurately.

  • 1. Measure a Radius Accurately

2.1.

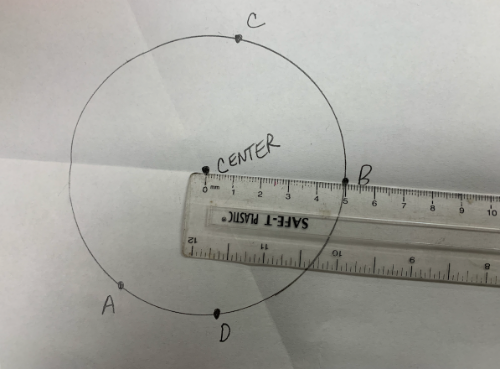
Measure a Radius Accurately

In this cup or bowl modeling project, it is important you measure the radius of both top and bottom circular openings accurately. [br][br]Please follow these steps to do so.
Trace the opening of the circular cup or bowl on a piece of paper.
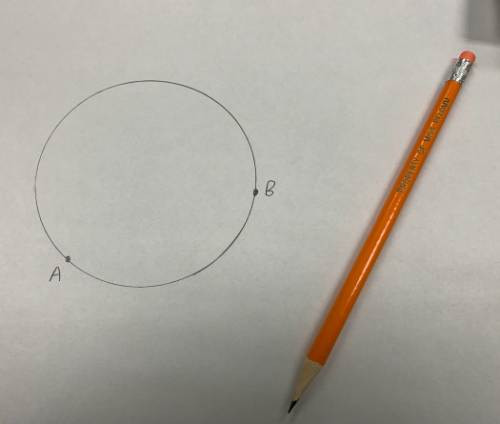
Plot two points A and B anywhere on the circle.
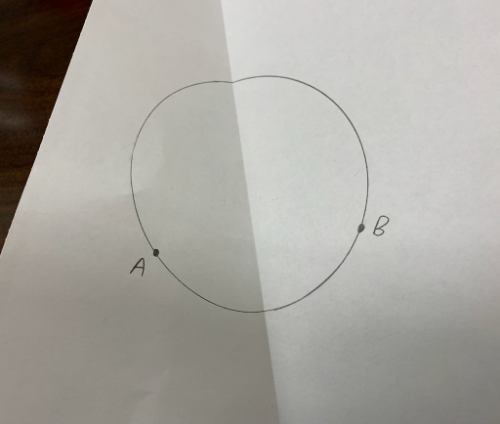
Fold point A directly on top of point B. Crease sharply. Then unfold.
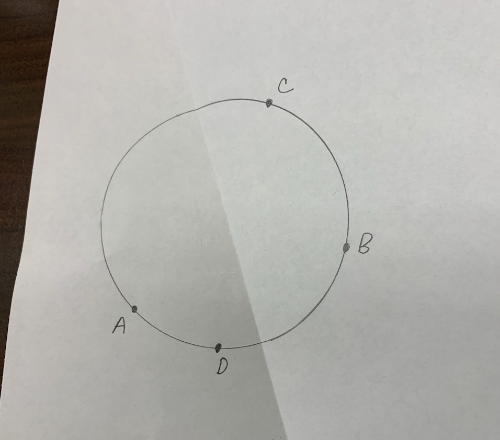
Plot two new points C and D on the circle.
Fold point C directly on top of point D. Crease sharply. Then unfold.
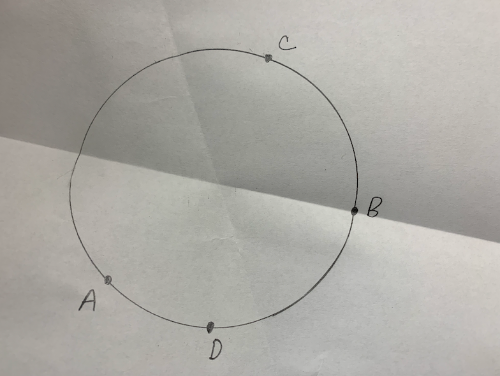
Note where your two fold lines intersect. This is the center of your circle. You can now easily measure its radius.
– Tim Brzezinski

Información