IM Geo.3.1 Lesson: Scale Drawings
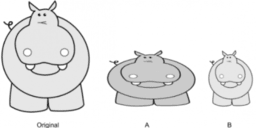
Diego took a picture of a hippo and then edited it.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAnkAAAE+CAYAAADxvAboAAAgAElEQVR4AezdB7SkVZU24N+RnBRRFAkCEpUkOUnOoclRMkiQnINkUEAlgyQBQRAlI9jQIIKEBgVBVFTGMI4TJLTQJJVxnO9fz5k5bXVxq26Fr+LdtVaturfCF94T9nveHc7/K+IRCFQh8F//9V/Ff/7nfxavvvpq8c4771R9Gv8GAoFAIBAIBAKBwCAg8P8G4SJ7cY3/8z//U3j+/e9/T6+9uIZunzPf84svvliccMIJ6fnb3/42YdDta4nzBQKBQCAQCAQCgUB7CATJq4Efcjd58uTi3//934u//vWvY4Louec333yzuPjii4vFF1+8mGeeeYrLLruseP3118fE/dfoCvF2IBAIBAKBQCAwkAgEyatqNkTnz3/+c/Hss88W55xzTnH22WcXf/zjH8eEmvXGG28Ud999d7H22msXM888czHDDDMUG220UcIC0Y1HIBAIBAKBQCAQCAwOAkHyqtpKDNrTTz9d7LrrrsXcc89drLHGGsX3vve94i9/+ctQq1n//d//Xfz4xz8utt9++2KOOeZIz+mnn7742Mc+VlxyySXFK6+8UoVU/BsIBAKBQCAQCAQC/YxAkLyq1vnb3/5W/PSnPy223HLLYsYZZyxmm222pGzddNNNxaRJk4YyRs89/8d//Edx9NFHF3PNNVex4IILFsccc0yx0korFXPOOWex0047Fc8///yYUDOrukP8GwgEAoFAIBAIDCwCQfKqmo6i9fvf/z4peZSsaaaZJrkul1566RSrJilB9qkkhWF4cE+//fbbxeWXX57i8JDaAw88sHj00UeLz3/+88X8889fLLfccsVdd901ZmITh6Fd4x4CgUAgEAgEAoEgeVV9AMn7wx/+UOy+++4pJk0CApflrLPOmgjPscceW/zyl79MpUUGnei5fm7oBx98sFh22WWTi3bTTTctvvvd7xa/+c1vivHjxxfLLLNMUvfOP//8QszeoN9zVXPHv4FAIBAIBAKBwNAiECSvqmkpW2rE7b333sVMM81UbLfddsWFF16YEhA++tGPFh/5yEfSZ4888kjKOuXqHMQHsubaxR+OGzeu+MAHPlCsuOKKxTXXXFP86le/Kv7t3/4tua033njjRHCPOuqo4uWXXy6Q4HgEAoFAIBAIBAKBQP8jECSvqo2QPEkG+++/fzHLLLOkeLSJEycW9913XyJ3YtZynN63vvWtFKc3iOoWsvav//qvyTUr7m6++eYrTj/99KRSis/zfOGFF9I9u9+99tqr+N3vfpeIYRVk8W8gEAgEAoFAIBAI9CECQfKqGgVhUxfu0EMPTQoW9+UPf/jDQlFg6t1JJ52UYtdmn332FKumzIrPBqnEiHsUW3juuecWiy22WPH+97+/OOigg4rHH3881QWkZCJ5XLaSMdzrjjvuWPz85z9P8YhVkMW/gUAgEAgEAoFAINCHCATJq2oUBAhhO/7444v3ve99xWqrrVY88cQTifxwYSI6CgQvueSSSen7+Mc/XhxxxBHpfb+jBPbzw/WpA3jrrbcm9yyCt8kmm6S4PMqemoCeSB7yKvmCK5fb+rnnnottzvq5cePaAoFAIBAIBAKBCgSC5FWAkf9E9M4666ziQx/6UFK6fvCDH7xL4br//vuLDTfcsPjgBz+YlK6tt946kUEEqp+JHiKa4/C4YVdYYYXitttuK/7lX/4lxSJWkrxf//rXxeGHH56UvlxGRWZxPAKBQCAQCAQCgUCg/xEIklejjZQUWWCBBYoPf/jDxT333JMybjMB4s5EimSlStCYd955EyH89Kc/nQiT70lqQBb75eFaXJPyMAcffHCKwXN/smYlWlDu8v15tZ2bLOLPfOYzyW293377JQwi8aJfWjSuIxAIBAKBQCAQqI9AkLwa+Nx+++2pfAhXJfespINKEoTocd8++eSTxSmnnFIsscQSyX276KKLpu3QfL+fVC/q4muvvZZInSQL+9KKOxRvWE3w3Ge+Nzt+cOmefPLJxauvvtrXKmWNpoy3A4FAIBAIBAKBMYlAkLwazS4Ob5111kkER8ydTFPErpLo+Vsc209+8pO09ddaa62Vas0tvPDCiUA5xltvvdVzYoTgqYdn147ll18+uZhtXzZhwoSkSFbfU74v5HaRRRYp3M+1116biib3kzpZo+ni7UAgEAgEAoFAIBAoiiJIXo1uQMkSh0bFEntnq7ORFC+ECPn753/+5+KOO+4oxObZ+1U8n2QF+96++eabPSV69uN97LHHivXXXz/FD9qu7IYbbnhXHF4me+5TgslWW22VtjVz/xTLcNXW6CzxdiAQCAQCgUAg0IcIBMmr0SiIGRelGnKUrAceeCCpdpkIVb8iRuL0bAd22GGHFXPPPXdSzCQ23HjjjameXi9IEuVNbJ3YQcRT/ODFF1+c9qIdSZl0X1zNCkDb6YNb98wzz0xENlS8Gp0l3g4EAoFAIBAIBPoQgSB5NRpFFup3vvOdYqGFFkrJF+rhSVCoJneV/+c4PdmrCguL01OGBUmUrSvpgdu0W2QJqVTYGUlD2GQCcz0/++yzKbGi8tr9jahyP1Mk11577VT0mcv6qaeeStddA6p4OxAIBAKBQCAQCAT6EIEgeTUaRRwb0obscNluscUWyeVZS/3KhMnnOTNVhq44Pb+3JZoMVXF63SJ6kydPTiqiODxkU0FjBZ3tzTvSfVAiKZbczBJOENyrr766cJx+LgtTownj7UAgEAgEAoFAYEwjECSvRvNT26h5FDwuS2ocN6cCwbVi8zLRy6oY5e/mm28udthhh+S+RfS23Xbb4s4770wKG6WtlqrnfZ/L0HUd6u9J4kC4qHNImrhBT+f705/+lGL/EMj8/Ycffriw96z9dmXJUui4YqsJnvtxX65LyRT3S/k744wzkvrYCzdzjWaJtwOBQCAQCAQCgUCgQQSC5NUBSl05CQjUOIWDt9lmm0JhZEpYJaGr9zf3J7LFTYo4UchWXXXV4sorr5wSp4fQUco8ESrPt99+O7lOlTjhNqaofeUrX0lxgkceeWTahuyAAw4oPNW9O/bYY4uzzz67uO6669I1PvPMMykOz5ZkSy+9dCKoSGclwfN3Jnh+t/nmm6fEDNd5zDHHxF61dfpGfBQIBAKBQCAQCPQ7AkHy6rQQ0oVsXXXVVcndKmnBXq4//vGPk0u2kjDVInq+g+iJ00PSJGJw337yk59MREpWrvp19pKVwYps2Upsl112KTbaaKO0rRqSRkmksCnOLIGi+ilBhFKo5Ins2TXXXDP97zfHHXdcuuas+rnWHH8nUQSh+9SnPpWO6TziCZWMoQjWUhrrwBYfBQKBQCAQCAQCgUAfIBAkb5RGQPSQtL322itl2iJ6FLNf/OIX6X3xd7UIXuX7voc4IXF2xkD0ELYtt9wyqXKbbrppseyyyxb2wvW+GLqZZ545FVieZZZZ0v8I21JLLZVcr9ywSpx4brDBBonYzT///Om4fjfDDDMk1VA9vIceeii5dRE7RE8CiJIw1ETlUeaaa660q8UyyyxTXHrppem++m3HjlGaKT4OBAKBQCAQCAQCgSoEguRVATLSvxQtCRMIGfKFbO2///6pmPDzzz+fiFOlqudvpK76PSTrN7/5TTF+/PiU3IDMcQMjfI5LjUPUZOUibvvuu2/xhS98IRFDhYsnTpxY/OhHP0qqnAxZRZg9uWZlwD7++OPFrbfeWpx44onF6quvXmyyySbJ1ZvjCO1F6z4khLgXO184t/vZeeed0/2I7RMHGAreSD0h3gsEAoFAIBAIBAYHgSB5DbQVNU/Sw3333ZcSJ9TAk8yw2mqrpVg7ipgEC4kNt912W8potS3aSLtkIHqUNHF6thXjWkXIZLSKq3Ose++9N5ExRE6NOyRNHCDi6PeeCGR+5vd8LkMW8aTe3X///YlUep/yiNwp1kwtzEqhezj33HPTb9QGDHLXQIeIrwQCgUAgEAgEAgOAQJC8JhpJfB4l7aijjkoxdTPNNFNyc1LkxMJR4BZffPFiwQUXLLhfqW8IVqXbNv+diRdi+OCDDxY/+9nPCkob1zDSlr/X6mtWE/3e8Vy3bFmxetTD9773vUnFO+igg9K57YoRj0AgEAgEAoFAIBAYHgSC5DXRlhQ9JUqoZcqNSJBA5hZddNFEmKaffvopsXCbbbZZcc8999QkeUgY8uVYmdhlZa5VYlfrd45LCRSHR2mUPCLRYtZZZ02qnt0wbHv2xhtvhJLXRH+IrwYCgUAgEAgEAv2MQJC8FloH2ROnh1QpcSJujpI37bTTJrK3xx57JDLFbYpg1SJf3X7ftSCUyF4umSJL104Y4vfuuuuuRPSiLl4LnSJ+EggEAoFAIBAI9BkCQfJabBBETwYqwqTcCaI0xxxzFCeddFIqhSLurgy3a9lEENFzXeL8qHeHHHJIqt8nRk/9vuuvvz4VW47YvBY7RvwsEAgEAoFAIBDoEwSC5LXYENSuSZMmFV/60pcKZVUkYyhSrB5eM8WSyyZxjR4P2VNORc0/++oqnyK7VyKIwssvvfRSIrEtwhM/CwQCgUAgEAgEAoEeIxAkr8UG4K6VBbvyyiunWna77rprobDwIBC8SiJI1bMTxhVXXJHq74nTW3HFFYuvfe1rxauvvhoxei32j/hZIBAIBAKBQCDQawSC5LXQAlQ8Shc3rVIq1K9vfvObaRuwRly0VDQJFzJelWVBDu18UbkjRSUR87ffIJC2Wfv+979fPPDAAykr1ns+q/5+M//nTF/EzhZusoXd00033ZT2xA3XbQudJH4SCAQCgUAgEAj0GIEgeU02AMJDxbvhhhtSLJuCwooPP/fccw2RLSRQqRQ163bYYYdivfXWK3baaadUH08ZlZEIm/cQQORODJ2MXjteiP9TALkMouccavJx1a6yyiqpzIqdOb773e+mrd2C6DXZUeLrgUAgEAgEAoFAjxEIktdkA0i4kFRhOzD15tZff/1EvrzXiHpGwVPw2B62kh2oZocddlhK4JD5SlWrJnreE+u3zTbbpP1l7VIxbty4tHMGgufcvtPI+et9xzEUcL7ooouKJZdcMl2fnTHsqKF0TDwCgUAgEAgEAoFAYHAQCJLXRFtRs2z5ddlllyUVT7LFmWeemZS5Rty0CJZEB/vgzj777KkgsRIm55xzTiJqVDlqXvWxqHiXXHJJscACC6TfqMenTAvyheRx+dourR6Ba/QzBJNL+OSTT56SUKL4s2xcbupQ9JroMPHVQCAQCAQCgUCghwgEyWsCfCSH2mVrMCqe+LXvfe977yJl9QiV+Du/n2WWWYr3vOc9xXTTTZeSN2TmKkrMPYq4VR7D/0iX+L9/+qd/SkTP1mT2zz3ggANSnT7ksPI37fztHm2ptueeexZzzTVX2sXjqquuKiZPnlxQMuMRCAQCgUAgEAgEAv2PQJC8Jtroz3/+c9qj1vZlslAVQVbwuBlCpa6ePWuVK0HYPGeeeeZEppA/e85Wu179/41vfCORLQWX/QY5pAIutNBCKb5P4kYz11Hvu9Q8xNK2bGL/qI5bbbVVqqtna7dQ9JroNPHVQCAQCAQCgUCgRwgEyasDPNekZy58jEhRzpAre9Tac7ZadatHnnwm7s7OEnaYoOZNM800aSs0xzv//PNTOZNqd63/kUNuUzX5EDy/cx1KtzzxxBN1M3NHu6aRPkf0fve73xVf/epXi4UXXjidl3KI+Mks5raGS8aoDozxUSAQCAQCgUAgEAj0AIEgeTVAp1a98847yUX55JNPFuedd16x/fbbp7g4CRMHH3xwil2rJmQjEabK93xffJsae4oQy5a1B65s3Z/85CcjJl5kZe2pp55K9eyOOeaY4vDDDy8uvvjiVH5F4oXvVJ6n3b8dz7Xatm2fffZJSiN3sRp6soG//OUvp8zeV155JWUbhxu3RkeKtwOBQCAQCAQCgR4hECTv/4CnSGVixy3LRXrrrbemODnEhoLGrUpB8/cdd9yRkiVaJVOOL1lCLJ1ixBTB0Qijz2Xn/uIXv0gE09/eK5vgVd4TNU8NQNnAFETu4plmmilhoJbefvvtV9x+++3pGrhyEeNw5/ZoNMdpA4FAIBAIBAKBCgSC5P0fGNyPyI0MV7F2SqPIZhWP9oEPfCAlPSA3733ve1N8GlWtOnaukhyN9jdiltWyZohaK78Z7Vrqfe4euYoPPPDAhMUMM8xQLLjgggkb7mLYwAlelEn4vfjii0ndq+hn8WcgEAgEAoFAIBAIdBmBMUvyKHeI3euvv56SJ2677bbkAl111VWL+eefP5G6RRZZpFh77bWLfffdtzjooIPS++Lozj777KbKptQjUf3+GVKphMs111xTfOpTn0pq5s4771x85StfSZisu+66BZzU+0P21lhjjeLoo48u4Km48htvvJFwhnc8AoFAIBAIBAKBQKB7CIxJkodwcCuqB2crL9uTISpi7TyXXnrplNAgEcIuE+LSqHvctIsuumgiMBQuBKjfSVpZ1ycuEU6UTTthKB1jlw+v4hV9ttRSS6XPYSgDWS2/a6+9NrmX7RISRK97AzvOFAgEAoFAIBAIjBmSh2BIDhA3xv2ImNhBYrHFFksq1Ec/+tHkcjzhhBOKG2+8sZg4cWJSomTDSoigXnFP+s1jjz02pggeoihZhHpHrZtnnnnS9mdiCeHjFV6SR4477rhinXXWSYSYuveJT3wiJazYRQMpfPPNN1PMXgy9QCAQCAQCgUAgEOgsAkNP8pA7iQC25ZKoYOcIe78iKxSnD37wg2mLMtmido6g7iEuOQnCK1JHmVIY2H6xEh/KUsgG5ThctkrGSLYQh6fWnx038vXDCW4SScaPH5+UT8Wifdc2bOr5qbVHOZVkQtmLBI3ODu44eiAQCAQCgcDYRmCoSR6Ch0wgKNdff32x2WabFfPNN18id5Q7ZO/SSy8tHnnkkUINvJzhmt2wXr0nHk3xYu7Ir3/960nVyuRmrLzC4te//nWxww47FHPMMUex3nrrJVd2xgoO/ubGhhl1D64XXnhhItEIMlfvxz72sWKLLbYobrrppvRd5DvcuGN7Eoq7DwQCgUAgEOgMAkNJ8rhlM7mzTZg6b5Q47lYK3oYbbphcj3aXeOGFFxIJrCQrmbhRp7gpJV3YxkwBY79BYvJ3xtKr+z799NNTAgo8uWe9NxJ23kOuJV9QAGXebrTRRum33Lif/OQn07Zs3/nOd9IxlK3JxZU709XjqIFAIBAIBAKBwNhCYChJ3muvvZaKBCsaTH3jlqXcbbDBBsU555yT3K9UqdFKoPhcHNmaa66ZSJ4dH5CW7ModSwTPvSJtsmZhShFF3NT6G4nkZWx8Bkd4S9I488wzkwqosDJlb7nllktxfD/4wQ9SpnMUVR5bE1DcbSAQCAQCgUDnEBgakpeTKsSEnXvuuYnQyYalGkkEOPnkkwuqnpi7WupTJib5Fam58847U+atZAOlU8T11SM1+bfD+IqsqQ+oTAqXrd06xCc2QnphZmcO+N99993FiSeemMrTwBVhtEeuxA5JMZIzwoXbuUEfRw4EAoFAIBAYGwh0lOQx1MiXpyD7/HeZBtyx/va3vyVicM8996TSJ/ZanXXWWVOwPyJiRwbkAmlrhqAhg6eeempSAalX3/72t9Mx+oXAuZdm7qfd60bmuLe32267pI7a3uzZZ58dVRGtPi9ctYcdRbjCZThLzlBk+TOf+UxSCydNmhT19cbGHBR3GQgEAoFAINAhBDpG8jL5EmulIG5+KmGiCHFZD7F3SMMpp5ySXH/IAvVOqROlUJQ/oSCN5pqtJiL+9zsZoTJEuXrt5tBNUjXSNXnPNSBc7smzW9fknGIUEWeYSFyReQz/Wtc60vuu13VTRX/84x+npBg4Zxfusssum/bzpepJzLA4iEcgEAgEAoFAIBAINIdAXZLHuCJpjLjYq0ZqnGVy96c//SkF3J9xxhnFnnvumTa132233Yrjjz8+uU0pNRS4Vh7OgSi++uqrxYQJE9Kxufy4EJdZZpnkmpUggZA04kociYj4nRIhdnlAaA444IDkShzpu514LxMh2LsPsYDiA5EiZFO5F/vnenYrTtA1IWbi6hBpu4Hce++9be3hm4njww8/XJx22mmJqMtk5mqXySsx4+WXX06JNNo9HoFAIBAIBAKBQCDQGAJ1SR4iRalR8mL11VdPZS8mT55c98iIocQH9egQLgab63TmmWcubAmGMK244orFVVddVSCCzT4yiRTIf8EFFxS2IZNYIbZr++23L771rW+lWm3NumariRpydcsttxQf//jHE6FxLq7K6u914n9k6ne/+13x9NNPp5pzV155ZYphk/ihKDOV0pPbdNdddy0kLTSrprVy3a5LLTxtO/fccyfsuVxdayvHy7/JhFZ8n+PZKYPrVg1DfchuIxRZqm0QvWZHTHw/EAgEAoFAYKwiUJfkUdooRksuuWTKLhVwL2iey7WWCw0xvOuuu9LWYIgdY40kUvEQE/XSuFTHjRuXDHczRltcn3Orv6YYr90UKEorr7xyKlJsCzKKYyuu2Uw48ivFSvao67WXrfvmvs2ft/LquiQuSOaAERVMeRHKHIVOnBpih1x+6UtfSveo/Mt+++2X9oP94he/mAiWmn+yXCWSyFhV469VxbKZ+0DGkEm1AimnK6ywQnKJUxqbOU6t71aqeogdpRD++hDiBzO/1S+b6TdjdXDHfQcCgUAgEAiMbQTqkjykiiJGQaLCeSJs1D1u3GpD6//XX389xbH5LgJ27LHHJgKDNFFjxF5R9hTFRXJqkcXKZnFc3xPXd/PNNxebb755it+i9CCOSA+CVAa5ywSEavfZz342lflAZpCvdo6fVbBvfvObxd57750SDCQZeO6+++7FvvvuWxx22GHp1d6w6sipKwc/v7F37PPPP58IHeWMoqZtECPHztfdyVfncU6FjBFfsXMIH2Jd5nnhzAXtPBYHiJ62VsqGiujeLSaq+19ln4m/A4FAIBAIBAKBsY5AXZLHiDKmyNnWW2+dXK6Mrb8RvWpFj8JCqeLinGmmmZJRfuKJJ1LwvONw41LguFfFz4knQyRHe/gtMkPdUleNy3eRRRYpjjzyyOKBBx5INdgQgzLJDlJlhwzXKosUwWr3+K6RYue+ZeoqJmw3ja9+9aupfIgyL7JNEVdlX9Zdd91UuHnbbbdNRFt8I0JLybSjRE4oafe6GiVomeS5diSPK9X1l03ynEd7O657peotv/zyqc8ownz44YenPhm7ZYw2cuLzQCAQCAQCgbGMQF2SBxhETywUcoJ02PnBk8ok6UHyA1XvnXfeSYkZ4sfE4SFHBx54YPHSSy+lYyBq/paRSclDBP2+npLnM8dFaBQ2tv+pczP05513XkqM6FQsGpfqKqusklzLyJcYwDLIFPKC7FHEPKlSlDnKocSKH/3oR4UkBCqn0i9IFDetjNYdd9wxkT4YcuEih76PDMGhjOurR/gyyRP32EklL1+D88EKwUZuZTjbtYSyJ/4STtTdVhN4xvLAj3sPBAKBQCAQGH4ERiV5IED0qCaM6pZbbpkIHKImJu5zn/tccifKRFWIWBYqIoboSVZAAil+3G+f//znk5H2W2qV79dzuSGPEydOLPbaa69k2Bl4e6YiGYL0y1bvMrnwevnllxeLLrpochN+4xvfaDser/LYyEv1E/nLBLCSBHJzI7nq0YndQ/4QaaRX9in3N5eu2MlOEz3X7Bzw4G6nrvm7rJi8Sozy386ZVb3x48cnd7at6SjK3NrXXXdd6gf1FgvDP4zjDgOBQCAQCAQCgXcj0BDJ8zNGVAkVRE/82OKLL55ULtuFIXvipbgVFbadbrrpUiwb9YlL8oorrkgqFGKA4HG5Ms7ctyM9nEtsH0KDDCqn4bdKsTD0lCtEKBOBMl8RCuoa9U7dNoqj5AaqW5nnaeZYmei4ZySL6idGkBJKzTv66KOLq6++OimCvtvMsZv5rmPDBgGWzSzhheu23ezaRq5BuyC8+p/dMsQDWkjI1ObGt4gYKU50pP4V7wUCgUAgEAgEAmMBgYZJXgaDoiebk6HfZZddkrGlqkw//fTFjDPOWEwzzTTFe97znvTqfQQNEZRpO8MMMxSrrbZacdlllyXX7UjxeJQ9LjjJBuLSuH0paoiM+CxkqxNExjE93ZusVQqZ5BEZnuLzkIxGyEg3v+OaqGhUPoWDO0V88z3BRxwgUoUAy7ZWxw75yt/p9Kt7dK8SMPQPmdoWFvqH2FFhAfXU4dyP4zUQCAQCgUAgEBh2BJomeQwoQ6rGnVgpW4khbSeddFIiRlyq733ve1PihRg6sVte1dk74ogjkhL34osvpoSLamPsf3F7lD8KDZK49NJLp1ImiBaC0QmCRx3jEpW5K6gfeUBMkTwlTJCKfiR5CBU8EJ9uXJ9zUO0UtNY2YjS5ib3XiXYZiTDm+6XcURG5rJVz0c+0Ffd+dULQsA/iuL9AIBAIBAKBQGAkBJomeZUHyYkRb731VtqVQO02NfWmnXbaZHTFayFOEgi42ZCpWgVtBc/bBePiiy9OWZsUPAkW3JESEsokMYiC47kerl/112S1cj8K6udSRhy4n117N0nMSMSmX96DGeWQu56CJsMZKZakgnQh4ZRW3+s06XN87cKlj9wh5dpOzKi+Rg3WP6sXEpX9N/4OBAKBQCAQCASGGYG2SB5gGFHG1JO7TDA81y0CoHYdAojYUf+4Z0cyun6LyFx44YVTCi+rTSduT/xZ2fFwlC9uWQRB3GAuz6E0C9cf0uDcyr9wRZZJMPuFsLVyHZnkqe2nBqIEG6/IuLI6559/fvHoo4+mTOSy22yk63U9iKUdP6jEFOPZZ589ZeEi7uI6RwoJGOYBHfcWCAQCgUAgEAhkBNomeflAXrlhlbYQfycWj7LHdVbvQcFjwC+66KJEFpCGtdZaKxXCRfDKIljZzeeYdsawT6p4OwkEVBwPF3AAACAASURBVCBuYcWPlepA7nJyR6cVqZHIS7++BwuJF5Q7yQ/iFu3tq621m9jJjTfeuDj11FNTrB4FFgkrqw1r4eIc2owbWRKQhAwlfqjItUID6vXJ+CwQCAQCgUAgEBgGBEoleVQ7W4EpdExR4cpDDGo9qHqvvPJKUoDs8MBNyjjb6QDJKpNgUZZkpCKTiAhi5xq5l9Wcc05lYBCGMs9bi5gM6vuZ6HHPIla2YFMaR+2+rKQhfBRdZV4UfvbdThM9x9d+Z599drHUUkulUj0SQ4QMCAOgFscjEAgEAoFAIBAYSwiUSvK4ZH/4wx8mVy01T4yb8iPUumo3rf+pLGrpVaovN954Y3LRlpUp6jiSKgTpU+q4FiUNcMsqyaL0iGD9UO7+2HCGLKLniTiL0aPYaWfxlFzd3N9zzz13imukyqrjJwsX2dMenSLRrse1cBtL9JEERK299tpr02IiXLdjaWqLew0EAoFAIBAoleQhbuKgKGPitShlVJ6XX355qtgoxtb3lMGgpFHwGGNFjrlTyyABmYTIjFXyA9lg9MXdbbjhhin+z9ZsEXPXOLmrpz4ibwifLGj72eoDiLQEGi5xmGsHO3Rw+XZK2XMdsr71LRna2nyllVZK9RqpxhS96gVHTAOBQCAQCAQCgcAwIlAqyQMQNY8hVyxZUWQxW4LgFVLOj8mTJ6fYN58hg4yw+CkkgZGuRyYa+QyBQCQE5FPrFlxwwUQ2kA6kk+pkmzLKTxmEspFrGgvfycQacbYNHtK+9957F3aoQPa0g5hNLl6JL50geq5BH7IjilqOeWs6xZO5bu3AEopeHonxGggEAoFAIDDMCJRO8iglylfYVJ6KotTG5ptvnrbkQvQoeAL3udO4TRE9hY8Z/XYJV6WBZ9DF9yna67nJJpuk+nsKByud0u65xgJpa+ceEThkT9zepZdemmL2lKURr4fUS3yhpCL2vlt2eyB63MNcyMIGqMriBMVeqsUYit4wT2txb4FAIBAIBAIQKJ3kOSgDysDutNNOKQmDWqfmnJ0kbEuGcCk0LHbrqquuSqpaGUaeYReTxS3IVee8Cy+8cKqBl7dD64R61A4ZGubfalN4U02pp1RUBI/LHOFTikWsZJlZ1JV4Oj/XLZKpr1lUCAugGlOT9dN4BAKBQCAQCAQCw4pAR0iemCelUx588MG096xsW6qeLc022GCDpKzJpj333HNTLb12XbSMOXVOAsVxxx2Xiik7J7VQtiU1KQoalxN7V0miGv0b0eM+58IVr4fc2RNYcob+cN5556XM5064z/Ut9RplVVP0KInjxo0r7r777iB6wzqrxX0FAoFAIBAIJAQ6QvIcORO9Bx54ICl61Bs7Ydi/VoyWbdAY/XaVNQQPOZDVq7Cx7a0oNly1XLaUnHbP0SiZie/VJ5LaCtl+6KGHUvurTaitJN+ccMIJKWmjE6507S9Gz6LCufLOGPZCthdzJGLEbBgIBAKBQCAwjAh0jOQBi/HkFlN8WOA7kseoH3jggYmUUXfaJUZIAaVu9913T0V5FcLdeeedU8kOcX6UHOSi3fPE7+sTuEbx0Rba3e4oXPVqFlJ5JWVIkqH+iuVr9HiNfM859QPxmGJFET3npCiqnfjOO+8E0RvG2S3uKRAIBAKBMY5Ax0meRIuvfe1rKTZO7Tx7iyJ97ZIvhpuCx0WLHDDaXHG77LJLcf/993dlp4VGCEZ8Z2RySF1Tm9CuKNttt11y4SPosm/FblL8ylZg9RfqsSLNFF8JOQcccECKH0X04hEIBAKBQCAQCAwTAh0jeVQ85VQkPNh5QJatZAixUHaVaJf8UPC4aNVjY6wRPGTP5vSxa8XIxKpdzMv+PaKOzFHvtOPHPvaxRNYtBJC/MjKuK685K3r21/3c5z43pWDzySefnM4ViRjDNLXFvQQCgUAgEAh0jORRRhQi3mOPPVI2pa2mKHoyLdtRaLKhVovvqKOOSgH8meDJ4OQK9J1K4x5/9y/p01baTE1D7Wn/W8WTET2Zt4heO/1lpLbnDqb27rjjjik+T9+UmOE8dmeJRyAQCAQCgUAgMAwIdITkUfHUIpNcQZ2htJ1xxhnJLdauwfZ725SJrZKhyU2rVAsFj7o3klGP9/qX5OW24b4XH3fiiScWMq8l6my11VZp71ukrGziTu21r65yPmroUZuRSsWSIxFjGKa2uIdAIBAIBAKB0kkel5eMRQbTrhdZZXv88cfb3mGCoWfwKYLqntlFYZtttinuvffeKJHyx/4ncpnQjfSqbZH0p556KhVKtp+xEiuI3n333ZfavUyiZ7EgJlAG9qqrrprOpbSKzN/IuI2JMRAIBAKBQGAYECiV5OU4PGVL1l133UKixTrrrJMyXdvNmMwkQNkLOxdQX2xZZeusTgTpj0RE4r3OEkltjHwhekqqKGSt3qFsaUpt2XX0nI8qnEuryPwWq+c9bttQ9IZhiot7CAQCgUBg7CJQKsmj4k2aNCkF0TPOCy20UHH++ee3HYeHXDH+ym7stttuKYmD0iOOSv0znwUB6ywB6ya+WdE79NBD084Y1GDkS6JN2S55xPGZZ54pjj766BQLqIbjWWedldzDscft2J0Y484DgUAgEBgGBEolecqlXHvttanYsVg55SkkSLRLwvyea83uFTnGDwFgnBnpbhKQOFfnySSFTYyeUjt77bVXiumUkHH66aeXUkC7sg2dSx+aMGFCUgw/+tGPFhIx7KdswRJq3jBMc3EPgUAgEAiMTQRKJXni7tZff/20Ly2XqgzGsgoeq50mdooLWLC8OC1EoNJgx9+dJ2DdxFjfQb4233zzQg295ZZbrrj88ssT4UfOyryW3/72tymOdK211kqxnptuumnabzcKJY/NiTHuOhAIBAKBYUCgFJLHrcXgKjIrk9bm8zaFp761q+I5rgK2dslwbEreNddck0prlGnk41j9RxD1HeRL3OXaa6+dMqm32GKLUmI8q9vbucTiffnLX07ZvRS9gw8+OGWE//Wvfx2GsR73EAgEAoFAIDDGECiF5L311lupHIWtyyht4qeee+65tgledttxAduKSkFlZM+G82WQx2pDH//3J9FTW/GCCy5INfTmnXfeRL7KCAOobm99StIHcmd/W6VcLrnkkuLFF18Mt+0YmxjjdgOBQCAQGAYE2iZ5YpYUrFWrTrIFl5odDATIt+tS444Vd7f33nsXs802W7HCCiukY0fB4/4jY9WEqaz/M9FXQ++QQw5J+xOrj3jFFVd0xG2r3yrMbE9dCR8URKEBUVZlGKa7uIdAIBAIBMYWAm2RPNm0VDx167i3qCwyE8vajkrZlRtuuCEFwquJJ/C+EzsglEVI4jidI5/6gi3xxMopnyMuU33EMhYTle2GVDrXVVddlRYVyqogl1y5tumLRyAQCAQCgUAgMCgItEXyGD018ageM844Y7HtttsWjz32WGkZr7ZFo+LJ1JV0kZMt2lUIK416/N05YlYmttpcjOd5551XKJ9DZTvyyCNLCQuovk4Ksr533HHHpcXLEkssUVx22WXFa6+9Fm7bQZnZ4joDgUAgEAgEipZJHjctFe+0005LhlDhWskWAuXbjZfLLrrx48dPCYI//vjji5/97Gdtu4CrDXr8PxgkTzvpFxYR++yzT0rCWXrppYsbb7wx1WEssx2dh0Ko/9lD184bG264YTr3n//85yB6MXEGAoFAIBAIDAQCLZM8OwLIepUQIRZv1113LSZOnFgKCWNkucxOPvnkFIu30korFbfeemt6r0xjHscaHIKX20q/sGWebe3sb0vpVbpHn8nfKeuVi9bCRUIRNZmyZ3cVYQrxCAQCgUAgEAgE+h2BlkgeFc9G7ocddliqKcZ9RlGh4pVhYLnLZOeqtTfrrLMWe+65Z/o/6uINHikroz9UHoNK/Mtf/rJQDHueeeYpuFLVztP3yiZ6eTcM2eLK99iLWYzoG2+8EWpev89scX2BQCAQCAQCzbtrETxKxgMPPJBUPAkRu+++e4rNK4uEcZXZOJ4RV3NPHFZk1AbBy2RPP+NKtQigIu+xxx5py7Oydz9BGp3rlltuKdZcc820oNluu+1SvJ4iyfEIBAKBQCAQCAT6GYGmlTwEb/LkySnjkLtMLJ5itQxsWUrK73//++SGY8BXW221lEXZbpxfJgjxOvhkUV9QO+/zn/98qmfHdatAtvc60b72Rz7jjDPSgkP5FjX79PV4BAKBQCAQCAQC/YxA0yRP9X97iq688sqp8PH++++flI2yCB4DzlWr3h4SSaX5yU9+0hHj3QlCEMfsPInU1ywqZFvLula6h0tVgeSy+mFlOzqX2nnjxo1LpFL5FrUgjQXKdjwCgUAgEAgEAoF+RKBpksf4UVDyFmP2lOVerTSK7fztWLfddlsy3MpknHvuuR1TaNq5zvht58ncaBhT2MSF2urOokNyTpmKcuX5JXyI/ZPRqybkqaeemrLIbekXj0AgEAgEAoFAoB8RaIrkcdU++uijxeqrr55Uts9+9rMFQ1umK1X2oqLHshkXWGCB5KoVj1dpcOPv3hOsfmgDxEuogOzrOeecszjzzDOLF154odT+mO9TbN6zzz5b6PP65nrrrZf65ttvv92P4zquKRAIBAKBQCAQaDzxAsF78803UzySHQcWWmihpJyIn8uGsIxXZSt22WWXFOROnSljD9wyriuO0X/EEvHiopX4IwFo++23Lx555JHSinFXtjk3MJX5pptuKpZZZpmUFKSkCuXQ2IhHIBAIBAKBQCDQbwg0rOTZ3YJKojjsdNNNV+y2224pVo6hrTSG7f79xBNPJJXEXrVq75W1RVq71xW/7z+Sh3hRfrn0uWyVOLnuuuuKshceue2dT23IAw88MCVhUBAnTJhQyLSN2Lx+m9riegKBQCAQCAQaJnkq/XONcaGKxxOfxF1WdqD7nXfemQrdvv/9709uW0a87HNkox2v/Ufcmm0ToQJ33HFHKnEihvPoo48ufv7zn3esz+iP1DzlW+xre8IJJySFL2LzYjINBAKBQCAQ6DcEGiZ5yqZQ1mS8rr/++inDthPk68orrywWXXTRVP9MrbyIxxt8ItYscWv2+1y2++23X9rPdp111ikefvjhVN+u2eM08n3KtWzvQw45JJ1PSIHko7/85S/9NrbjegKBQCAQCATGOAKjkjxuKFuYCTpXI0xm4YknnpiKHzdiFJv9zllnnZX2Cp1rrrlSwWUxT80eI74/toih+nhf+cpXUpyocirf/OY3kxu3E/3AwkZs3vXXX1+sssoqiegdddRRKTYv1LwxPpvG7QcCgUAg0GcINETyZBB+8YtfTFuMqV93++23dyTuiQE99thjk1q42GKLFU8++WTHFJlOEIA4Zm/IJdLFZatmnlhO2dk//elPO7o4eOqpp1JtPlm9xoS6eUIa4hEIBAKBQCAQCPQLAqOSPJmD1DRB5vaR3WmnnUrdwiwTIwTPeRS1nWWWWYo11lijeOaZZzpSDiOfM157Q8rKxl1cnr5iyzEkb4cddkilfso+T+XxJHdI8pBpKzbvtNNOSwpfvwzsuI5AIBAIBAKBQGBUksdVe/PNN6dki7nnnrv40pe+lMhY2fF4jmeTeTtczDTTTGl3gSifMhwkrJIcdeJvfQfpOvzww1O9PMraXXfd1dEFQq6bp9xPrpsnFlAWemTaxsQaCAQCgUAg0A8I1CV5jBUX1D777JPqkK2wwgqpZETZBI/hp8b88pe/LHbeeedixhlnTEkesiTLLLTcCYIRx+wPIqqfXHjhhSlpRzmVTmV/V7a3pKBLLrmkWGKJJVIJF6VcXn311aib1w8zW1xDIBAIBAKBQP1iyFQ8xCu7avfee+9UnqLS0JX1NyNNudt2220TybOzwPPPPx8k74/9QaLKaudOHUf/UX4nJ0PYek/f7eQiwbEnTpyY+iyXrVAGsYDq5sUjEAgEAoFAIBDoNQJ1lTxlIW644YZi/vnnT0re1VdfnWrjdcJQc38pNLvVVlslknfAAQeUvmVaJ647jtkfJJS6LBlis802K+zIYhcMGeGdJHnOqW7el7/85aTkcRPL7FVuKB6BQCAQCAQCgUCvEahL8iZNmlQceuihqWbdwgsvnIxo2TtcZJLkuE8//XTaUYO79uCDDw6SFypewxmyCJfdUajNajlutNFGxeOPP57iR3Mf68SrfvvQQw+l4sjzzDNPigsUHxhxeb2e2uL8gUAgEAgEAnVJnqKvG264YWH3CQHmv/nNbzq2k0A1ybN11C9+8YuOKjGdMPpxzN4oe1lVO/nkk1OSkBCD8ePHd6TUT2UbOy+3sEWJWMC11147kb5IwIjJNRAIBAKBQKDXCNQkeZSIW265JQWyize66qqrOmowudW417beeuvkrrWDQcTk9YYwVZKYQfkb2ZIIIeFiwQUXLJZaaqnCjikKJXf6Hmzvpzgyd60M9EsvvbR48803IwGj17NbnD8QCAQCgTGOwIgkL2fVKoAsvumTn/xkCjDv5O4TSJ5sWjXOuGv33HPP9H8nY6o6bfzj+N0lqfqn5Av9dZFFFikuuOCCpLJ1uh2c97HHHiu23377NF7233//5DqWuBSPQCAQCAQCgUCgVwiMSPJsz8R9utdeexXTTTddIl5cp97rlMHMMVXcwkgegylTMUhed4lSp9q3G8fVV8ThUdS4TrluO73zhfty3hdeeCHttGHbPxm+9957b2TZ9mpWi/MGAoFAIBAIJARGJHlKQNj0fc0110wkTwFkWYSIWKeMtWMLWFeTTzFksYBiAoPkBclrtM/pQ9TgT3/608ltKmlICECjv2/1e85LzZNZq5akBAx76aqZFwkYMdMGAoFAIBAI9AqBEUmeAsj2pxXbNMcccyQXGBWvkySPgUXoDjnkkLQ11YorrpiybYPkBclrhnyJwdt4442LueaaKynRyqo08/t2vvuDH/wgFfP+8Ic/XOy4447Fr371q4IqHo9AIBAIBAKBQKAXCIxI8igQZ599dtquafnlly8Yr04TvGxcFbGV6LHAAgsUTzzxREddxPmc8To8RNLWeOI6uU25/PWhbrWvLNszzjgjuYoXW2yx4oEHHij++te/9mJcxzkDgUAgEAgEAoGRd7ygnu22226p3phtxhQp7pahVFh2vvnmS3uQTpgwoeN1zrp1X3Ge7hBJYQViSWW5jhs3rnj00Ue7tkARbnDTTTcll62EpYsuuqh4+eWXY5oJBAKBQCAQCAR6gsCISh6XF3cpV+1JJ53UlQzFTIK+9rWvFVQQ577uuutSWYz8Wbx2hygNMs7KmahZZ6GgIPL3v//9rsV1CmmgHCoDNNtssyWyqQxQPAKBQCAQCAQCgV4g8C6S9/e//7344Q9/WIgrkqF4xRVXFFxg3TL8d9xxR8FFrADzF77whY4nfLgvrmjqZX52yzXdLUz75Txw7TTWSN5RRx2VtuJbd911i/vuu69rLn/3pmD4EUcckcbPyiuvXDz44IMRl9eLmS3OGQgEAoFAIDC1u1YmoEr93/72t1OGK7KFdCky2y2ioN6YXQPe9773FZ/97GdTMduySZfjUV1kRHKxKQ8jm5gKwzWtHIZ79jniV/b5u4VlP5wnY/2HP/wh7XtM2YL1k08+mbC2FVmZWCN5xx13XIrplB1+zz33dI3kwVt/UQxZrT5qoiLiCiNHlm3MtoFAIBAIBALdRmAqJY+KJ7P2lFNOKWaYYYaUpfjII490NS4OCdhmm22Su2u99dZLruIySZZjIRVKa9x4443FiSeemMjkZz7zmZQZqU6fYrZnnnlmIrgIIIJS5jX0A/nqxjUgPEiXPYm//vWvF5JqlMjJWO+6666F7evOOuusRMZgjVi3g7XzqY/38Y9/vFhjjTWK73znO10lea6deqjvSiCiKnrP2IpHIBAIBAKBQCDQTQSmInnKPbz++uvFTjvtVEw//fTF7rvv3vVdJ7iGDzvssJT08YlPfCK5jhn+dkkJQ0u9U0ftW9/6VnHMMccU++67b3HkkUcW55xzTnHllVcmIvLVr341ETw11nwuJpEapBxGGdfR7n0Myu8R6eeeey5t94Xo2Kbu6KOPLtRcpG5de+21SfE6/fTTUwwdYu1vRYQpqa0qqEjeqaeeWiy00EKpXh6S1812088UYDZ2PvCBDxRbbrll2p6PQh6PQCAQCAQCgUCgmwhMRfJsw/TKK68UNnefeeaZEwHizmS4ukUunE9WopjAeeedt7jtttuSGtTu+RG8Z555prBVGyUJebv77rsTeXPPFExFoN96663ixRdfTIb65ptvLpA9W6whJox3N7Fo95579XsEzc4TSNsee+yRXqlbyNuf/vSnhLXSItyY8FT02j6zsOaiRwCVI3GcZu8ByaNEU/IURe4FyZPh696VcTGWvve976V+1c2BHecKBAKBQCAQCATeRfLESKlRN+eccyY3GnLUrKFt5/tUF2qOpA/XoF6fa2rnmIgEgqeGGRIhaxfheOONNwrElitNzFR++p/yMnny5OJnP/tZcf7556dMSUQP+eg2Ju3ce7d/q/0k7px22mnJ7a2kiGxt5HkkrKnHsEb+xENq7wMOOGAK0WuWVCN53MIKeXPXIvLdbi/ufbtfiMuTKa7fWEjEIxAYRASMUYsy4zdiSwexBeOa6yGgXw9z0fqpSB5jq4Cr3QIoIVyYragp7RALRl1c3rLLLps2e997772TgtbqMR2PsnL55ZcnN7SkEga30Ub1PUZb/T7xZHfeeWcpymKr99PvvxNXd9555yWCR4VF3hqNR6OkIoTc58j4d7/73abjIZG8Y489Ni1U1lprrXSMbpM8Y0YSDyWRGi0RRB+Kx2AioP+aB8yPXscK0XHfxqS+S4224OXxaHQ8D2Zrx1V3EwFjyZjqxbhybmParkjqmQ5rv56K5BnQSqZ86EMfKpZZZpni1ltv7TrJQ2K4bMUFqpWnDIbkj2YVnUyGKEt27BATZj9RBriZDqUjZPIhjs+TKtjq9eTrGrZXeCBT3LK77bZbUq9eeumlplb/GWvu24MOOiipelzkzSw0kDxxlvPPP39Kfrj//vub+n0Z7QIL6rOdNyyY9GXk1/3FY7AQMFdQobNCbQE6FogOgyc+29xroW3RL5lItYW33357aA3iYPXOwb9aJMt8KRb/L3/5S1fnSOq0pMBNNtkkxeE3I0gMEvJTkTw3ffzxxydytfrqq6fVWy/IjJUjQvaRj3wkubzEa7Wqxug8l112WSJ53Ig6UrOPTD4oUww3hcn19AKbMkhIJ46BiKkRd+GFFyasEeFW3Tvc5OLyED1YM7CNXjPVVsYuBc3gfeihh3rSTsimBYHQh3XWWScZy1bxaLa/xvfLQ8B8weUv45/r/XOf+1zx8MMPpwx9JMgCsJlFY3lX1pkjuRckVuKUMaicFYK3yCKLpDjp1VZbLSWiIb7xCATaRcAYEkZFGKCoidO2wOjkgtix9XPcgK341Kc+VSy33HIpUdB4HrbHu0iepASFiDfccMNUz6xR41rm9xh17oGFF144xeUJYm81AcTKW0C/jjRp0qTUuK00oo4hM1dntCsHMhEk7x87cCC9ytLIpOXahk2rA9XqzgpLbB5lGWFqtH9pF4kytjXbYosturqtWeU1MpLq5S255JLFUkstVdxyyy3JeLaKSSt9Nn7TPgIWvmKE1VycccYZUzKN9lRqSd9U85GrZxgIvL5pjlTAW7jEoosuWljsKzNlztt8881TCM2OO+6Yxmf76MYRxjoCr776aupfPC9bbbVVWkBkotcpbBA8/ZyQtNlmmyURiEp99dVXp/CiTp23V8ediuRZtVq5IXnbbbddisGoNFzd+hth4N6yLdUss8ySMjSV42hFzeP6MyGbpNqVg03mXIFq6LWa/dktDLt9HsRcRq1SKJIOXnvttZb7tEFIGYS1XU8kyTRKqK3Ott9++2SMGSOxcd3Gwvmo0XfddVexyiqrpKLICJ9En2GN+2i5sfv8h1b2lDtGQEkchsiOJuZHCi2FT6Y+Em9OoEL7zSC1s2ulzIm5o8Rb4C+99NJp3jVv2hrQHtDGooQm5E+8NgIci5Y+78B9fnnshCQ9fY5KbnyJnzeHdkJV01+ph2LzCVoXX3zxFEGBF5PdGbbHVCTPQFebDsmzklMbrhcGEtDUG5MnkieA3mqaOtLs9XAbMvoaVadpZ1KywqAInnDCCSkZxHU2ez3D+n2khjHQb8aPH59k91YHizZCiCgIsKbGNkryEMINNtggxcJJlKEI9gJzpHfixIlpoWI8KesyrDEfrbbzIPyOqkyhpgqLEaYu8zJw4V5yySUpNIHKt8IKK6R5RtKRPsd4+W2nXU/tYGicWVAZa2JXKeCUZwlDCJ1xTKl0P16vueaapOypeqDgePTndtCP30IA4Tr33HPTgsJCQtId9Viymrm8TIU893duYYs0/AI/kOyXq0HwGA7bYwrJAwClSukSK1Zut3ZLl7RqXBl0qp0gX7XGxIRQQjRGs8fUiOLolPJol+TpkArtKtFh1Rsk7x/uWiRP/BtixQAyHK0+GEZGEs6ejZI87aEMiz1jxeQpvkzJbbbPlPF9/TeryLPOOmuKL0T8GNV4DA4CjIzFpcWLrRa33XbbtOBE4CnXCB8VT4iCeUZdRKV7xPqI4fVbi8MyjVUZ6Jnvxd6Jo1WgXKwd9U4BeEq8ZDUxzAxiJnnc08isZCLeDPOh48QjEGgVAcKSkmaS0/Q3HjweEPHUCsojfsZPGf3MGFQDl2K41157pThp49MYICgYs/4ftscUksf4IHVimWTXUqzcfBkGr5VjIHpWjyZMK2hB+Ixmo4pOPic3rzg6yReywtrpLM59yCGHpNWGVUaQvH+QPATGfrQGkC3MrPJbfeiLVlR2PrGy0w8baXfXIFFjiSWWSDteMF4IYu4L3XzVN0xYhx9+eFo07bzzzmlhYKKJx+AgS8IjYQAAIABJREFUYMGhLyNxFg7IkLqHwgCQH09ESN/n1r3++utTNqpgbruuiPmhgFmgcuUKGdEHeqXwmf8ojK4FkeOyspAWVqBQPNJq3s3kzv0xvhZw1BUqnvJWCsX36h4Gp/fElY6GgPHASyfsYcKECYlkIVoWUIgfr4yKDUSDdhZKbAqyKL7fMdkJ8dvmaWEWQrpwHjZi2B5TSB4ADWyrNFmtYjOA0E3DWH0uRlJclonFJGQCapZYaUCTE7ef37ZqZE2OJj9xXjfccEPqjI0Qj+p7Gtb/KVfUTThTOw3UVgm1WB8GSHyfVR7CNxpu2sI5bUsno1VwvKzsVtTf0c7VyOf6mnNzexlTG2+8cbqnTsSZDNuk1E/3k0mRZATxyjwd+qXQhEoi5G/zA7LHQNlphdGQrMAFSuEzl1G59QsGh+FpdYy0gpFzMarmVaSV4i2+zq40tnqkTrqHTF69+p/xRQApffPNN18ylBZU8QgE2kXAfGjsIFmyuYVpmcv1L/2PR3H99ddPSU7m3VbtN9XZwgSPYCMIB+Zo5xHKJeQC8TMuh+0xheRZ3Zm4EDxqntVqM1mNjRi+Zr+DZDLyiy++eFIXXVOzWbbugbHnRrQiaEX6tWLVSQQhk5BN+M2SzWbvfdC+b2BqLxipq2Xl30o9MYaIpG6XEUZRnzQQR8PD+Q3cvCgQVyTOCPEb7bed+Nz16KsUZJljJheFtBHYeAwWAvqkRQxlWMwylU5mnj5eSfQqyRH1C2miUgju5gYVXI4oGh8MTS7FYk4y/9YifN73NA8hhr7LOOpLSJunsZaf+T3fYRT9xneNKyTTtbgH18PtqgA+ZdK9ZLLq2s1z5k5qtP7ribhKbnIN8QgE2kVA3zS/S2ZScqrS8yIEiCfOWJOESYXzv37ud/lhbORxoZ9XjoM8ToxV+4iLJc2hVriBMcjLwlPIplceNx9/0F+nkDxgWH1SzbglxGU0oqB0wkDmY2r8xx57LK2GZ5hhhhQXoxM0Q7BMznlFgABIJmm2IU2aVud89meddVbqJIx4vs54/V+3LUxy4Wk4MQbNrLwMVoMUOaMuiMPUXo20t3OLvyT7zz777CmwlsHS/r1qH+cWC0otscWZBYu+FI/BQwCpEaJx8MEHp/lRcLiAcf29Wv2qJHv+1g/NHxQDAd7i+tTloh44nrnWsbPxMj8ZN87paUwINVH2geHjnRB76piImMUrFeKee+5Jr/5n1FyX4xobQl2ocRRFipxF74033vguckeJtLCiqiB3SClCyBAqju8akM14BAJlIGDOxz2ENFh0mPurbavFu77KGyL0St/OSrjxYdyY4xXONx4trIwHY0O/NwbF1FpcGTfmZePIOPGeY1rkGGfD+JhC8tygSUg8HpdEDhrulYF0Xsada4MLUFweFxyXrQZq9Lp0GGrO7bffnlQ4q3HkQ8cabbLyOaOcSaLVhg7WK3Wo0Xvu5fcMSO5sagE1zkJB3zKY6z0YNoNVhX1k3NZkgm4R/epBP9L96SvamNpgoeL33FKNEMSRjlfGe66bcsKgU/MoOu4xHoOHQDZGDIlkIHMRdycihMibF5CunKyQVbHKVwRK/9YnKN7CSLhzkT2LE0qFz2S1iu0zfigP4oAFiotRQhApEuPGjUtPWb+eSk9svfXW6dX/Pnds3/UbSohYVQHtlBHnML48XTujmK9JNQLXpESMc3NzIZbZsI42lgevdeOKe4mA/mSuRrYseizW2VhztzkUKaO6IW36oz5NADDuLFzsZiXpKfd748B4yv8jj2JPjS2igWx5Hha/kS1PSJIAMhof6CVG7Zx7CslDZigNH/zgB5NBouo1Q6bKMIojHUMjIw0mVVm/JkLErxHDX3k8K1qrUzF1JmmTsWBOK4Hs0kA08ioaCZThaWWh45lkZf006y6uvIax8LeBCes8iLiDrJ6yS6oW1jK7GRrkUPFqRggZbwQzfQEZpB6q4yUbm8Hqh7biClMCSFyeCclkEo/BRcB8Ybs+MWyMjV0whAZw96jvxZAwRtQwT397IlOVip+/ET5zivg4RgkJ87SlpCxW/QZZ23XXXZMXQR0vfchigfJBAUTAKGwWOPnpf9dnvqM2IqJKRjCQvuNauGOFDyB81AwJJcaN0BjG8YILLkjX615DfR7c/jooV06pJuBkQmbeRPw8CQeInidbwn4bH8svv3xayOjXShfJcs9jDXHjisUdLPiNBwTPd3AAyUMyai3ahn3hPRXJE/NGMRO4Lti2H0geI29CxLq54bgbKGsavBECkL/j+0iDxrZiEFtnpWwiFksmg0717VdeeSVlGSMcCIpVLdJBAva9ZsllPv9YeYWPpwFFjYA119BFF12UBh3ixeUDa8TOIGbo1JGDtQFpgFu5NarC+R43PhevPkKB0H/7oa1MNBQVJI+R1s9CCRkU0/Pu69R2FoLUaQTIYoTCz63JDYqkSbTIT25678kU5x4yd+WneS3H7iF8SJfMdONBv2GoqIP5iZjlJ/dSflIIq5/5M9+v/L3zOa550HXbG9yWZTJsXavaYb5v0WRhZlE2rArHu1s33ukVAvqYBZQxkRc8FjvGkbEjjo4N1y9VAdGvuWLZZLaCXaH+4SyVT+/73Gf6vQWTY7JLCKNFt/E8zI8pJA+bpb4gedQQ5Aeg/UBOkDMr0lzDDxnF7pu9NkZfp0Aizj777LQ6FmeXV8hcuQKLBYCScSl4Vs0mvSwfN3vOsfp9xEu7MYLUBzhTO7je/Q9rqqzsKVhTG/Q/g9zAbAY3bUN5Vm5nttlmS8c0gJs5Rqe+q+9wszGiObg3SN5wTKkME8WfR0AfpCLIpqbsIfXmUSTKIpHyxi2aCV71K7duJn1e/V/9nbL+d+xM9syFFD8hEptuumlyQctmNE6pklR55VYY4CB7w9Fv+/UuzIsWTxb/PDErrrhiGkvZ3udFu1f2xTO/N9r87Xv4DPGB4k6tNh9TtY3fYe7bU5E8fm4uUbK9lWS/kDwMHgs3edoBg6pnImy0gas7gM5h8kJkqU0Ih9gXE5vAaAqf+ETnDPXuH7XwqnEc7f88GMXzkOKpFMg1tYDkrtSKUj0kdMqDFVcrber4ecslJR5I9NpttOvrxueMKSVznnnmSTsKuK5hnlD61YB08rq0JyJE7acUqI+H3Fkw8giMRtoqCZ7+Mtr3M9mr/F2jv8m/9er3+em85kMFj9W6lFgi4SKXthAiE27bTvaiODYEED3qGiFAooXwAnahcq5mI3ACdrzyfX+PRv78lojA0yNMwQLc4ovINayL74EgeRqGcbSDgZhBcTBWn2TZVkhB7gxIrOP+/Oc/T8GeJjxBmUiDjqUjtXr86s43lv838GBN2YM1lY2RKQNr7UNBEVwu4UIAOnKu7foBc/dKEUY+LU6sJIPkDYdBYxS0pT4onlmYgBIrtgfzv0w/5KmSWFX/bXHDjUu5sFARImJfWLHAfmtOqv6N9yzCLUTF8yGTFksMIjdWJm7Vv6v3f/6N6zGelE6xEKPuidcT3iIG0FimXg6rQRyOnjm4d6Fv6fcWGUJ82OdKMoegWYyw/8hZpdeHcCNh1NhjW2rZAMejvBtDFjQWZsaNRcww9uupSF6/umszKeP6E98i7oo6kv30/WDM4xpaV/xaxY5xNQnYQxTxl8EqkFzMRr+Qc3EjFieujYtAnx32GJDBNTHNXbl2FGN59dVXp1hhscyMhlImYuTqkSqfIVbi8CQbSSyj9jJu3EkWBxYrSJfv5WP5G3lECJEv/QqxlKnrfedF0ip/k3/bzKvfixMUuycmiqrn6W/Zj5QPBHcYjWJzvSC+XRYC+pJkR+VOKGzmzup5XL8Uu20uFbuK2CFtvmfRY0wIj+CGReTq2RYikfHlXBRrIWDCEobtMYXkYbFWkDnxwkoSCPVA6uZnGlEjyKSxh6TsGCnUjHw3ryPO1X0yVwtz6qBBaiX2/ve/P20hJcaoX8IMXLfsLWEAjLEyFgxkkLzBnkYZI0/JQ+YghkW8sLmpngJXTbIoFooiK8Vif+Npp502hctw9XIliVMVF8cVm3/LyIk/lSHIqzH99NOnEJZcy87i1zErf5N/2+yrYyCNFA9EVqYvIrreeuuljF73T3kJsjfY/blfrl4/skCxYEfgKlW6bAP0RRngPCPcufa3N98jesKslICTWKGMisLJlSpgPkZ+xSlwHMe01ZmFE/Vv2PrzVCRPzFQuoWJy6TeSpzHFdlHzPvzhD6cVsImoXkPmBo3X/iFnZbSFASpOiIpHBZHYYJByh/ZTf+CeFucpCJ87T3+VsRiP/kUgkzhkHImxAJZpSrVjBPQ7BgTBQ3goeLL1xOSN5p6tJFoIm0WJ2FR9g/FSOFtWoZIn4uOoeb6Xf+dvriXuXYbMXJiLbTuG2GLurDJIXuU5kT0GVU0yMduC4iVOuWeuMYoKeyFoXiA7pQ92OTsXpvEIBCoR0CcoZ8qn2I1FhQT9S4iA0B5zfLWtsGimJiufov/rl+Z739UXlTUiAMkc1ydHOkblMX0uNEtyh7FMRTe2vS82cBgSjqaQPFktpPlcDFl8x2hyZyVY3fgb8NQ8GZmMusnNCrPVgP1uXHOcozPkkrG1ArMBvExGRV65870/2sDuZpsoESOImGFUYNakFCSvcqrvn78ZHat47cPw6EtcRtQ5MWrqMHLHivuknElSk83NdYTwUZUzMWr0FWlDDLlaKXRq3DFWsrIRtUqCV3lMnyF74vnEIeWyK45V6zeVv2/2b8d0TqRU9QGElIrI88OoMsxqiSKZDCaXte+bm20JmY1lkL3+6e+9vBLjzOIpx9EJN1AdgVIsAXQkFc+8jdDhAPqj2HljNM/n/rao9lkznIC9QDC5gS3GXYdsc+5f71vgud5BfUwheVZdJop+2tYsN17lq9WiiQ3r5uLgT7fa7SfVsfJ64+/ySZ6BLrZNYDjZnpohAN0A7yeCp+1NRMgBkifeChEIktf76TITOotbkzgFSlshMTwa2oxiIBRAUg/VQNV85X6UA6JkCRGwm4nyTtXFjlslUYiRZ6NELX+/md80e22V30cic21AIQj2OrfAYqTFQknQUOcMXuZmpJiSLRQI8UOajQvEj5Gnlgbx6/146MYVIErIPkXcPMgLIx5V6IFX4QDmSAvheiE35vjKZ7axle81aweEfVHHhUqot2qc67/iAyU1Gd/mCPPFoBG+KSQP+Pzh3KBzzz13Wo1hwxnAfnll4LlLTMKuUywMN10/Bdv3C1bDeB0GrwHJaJDshRcYlAZhPxJ9xEHZGCRP7Bb1JUheN0zK1OfIpC67YLlijA/9hosGoUNMFDW204QC1gwPgiLGTWYpcmOOFPsj2cHc43fVRY4rSdEw/o1QUg+5qO1zbitBdQAlalA9lUSi5pmjZZbDlfGkZMOVS84OBcpYUGy4dxlP44IB1VZB/Kbuv4P8Xx57xhx3qwxyyi8FPG/lp+/oF9ysvQi5QSqp58a86yMcKX/EC0Ph02/NBcZzLhI+KH10CskzwKweub6szmxr049JDYw8osdVJ26Fe5nrxCqxGYl2GAnQWLgnbSxe1PY3CJ6VX66Lp1/0GwaVJE+dx1DyumuuTMQWsAyMlTgjozYm1UkiDIKC1Fm1U4aREwTGBC/+FwlEzKkLVCwuHKRFhr/Ab+SvFTftoJM/BlGojIWLcYjwIbswghVMGErxgdzP4vkopMq9KDGj4DLsxRFKMqHq+J35ncrHszQoRrS7PXqwzoa0i880b6tHq92VktJ39BHuWmFhFHRzuj5isd6sEtfuvM92uBb9E9nUvy1AvKdfut6dd945Xb/vcOOaUwYhiW4KyXOx1DDqGOLkRvi+2wWvU79HQNXDEaSsQLIUaBNMv8Vkder+x9pxDXqrLbWRKHcUZwHvJg6u237FA8nLMXliPUwYY1XJyyt6c41nJ1Qbx4QvVyCyYOsxxI7ShIjYemzhhRcuVl111RRDxhVj0SAmDpmr5fa0ADbxK+RNveKqlDDBUDXqWh10Yld5/XCiaiLL7IV5OO93W/m9/DeM/AZeVBuEEKGWkYzoia8W58dlpwyStmB4ldRAEhB1fSaIX/dJHszz2M1jdrSr8D1E3TahBBhtjNSfc845KVEHscuLcnO7hToCSAnuNsHLtsP1qL9HPLLIy/F+3kc8hRpQ8S1sZOOKw/VZDjsYDZNefT6F5GlEDWLyElAs8BDpywD02ytwGVDXmdVHcmovpN5+w2YYr8ekwMgyCtxkAnT9zXjUi9/oNRZWfFwSAnq5Ahm6QSZ5zU72Jja/YaAlMyi7IZNOu+RMTAbcd9p55HPYeUI4BxUOWRBPJ27OhuYUOJuSm5x5AhAOpNvisBa5yyTF96h41D8qnuNKkug2wXO+/HTNlc9G7iPfTxmvzk2Bs+ctomebKGO0HiY+87tKxY9aql6gsAYxkNR53hlGX6yfJEAZj/oN4oBAxKNcBPK4rj5qHldclBZMxpf5q9549ZnvIercr9qTnTaGzOOVQkxevBurYjl9p5U523E88YL8bOU4VHxj++abb052JRNOr67b9athKcFI/8xlk8QZ9mu/nELyNC75UY0ZAcUkdISpFaC69RuNaTUpbdrEKxiaukdizY3TrWuJ85SfYAFT7WhgMcomCrFQCJ7+qe191s9tTWWk/lAdrf5MEAjPID6QNMaW0ZUJSunPLouRJn3vIXBUd99Xwd5CDNFSO9ArlRPpQsysiJt5wFEsF7XHXGX1LdZL3zABc/9IBDjllFPSvMAlhIQgGPWIyEgEiNvRccRW2rYMIeGOHOm7jb6H7CCajuPp2vKTgfT0P+WLgi2GDRlCNrmcqQ4USk9/c3Uhnn7X6DW08z0YajvxVbKMGUdxi+6rmeM6jjZx3e5TTB+Ffv/990/Knng+6opxdOONNyYiYMzrj2UsEJrpc8P4XaTNGOVWR6Rh6mH8UlG1p+Qi+EtwQ8q9X/3wfSTcnKwv8q7JuNZm5oqRFuNsuIUwMqgupL9r2VJt7hiu1ZML2Ku5Qx+iDkseNUYogq3EaMNAXzO+RnIb52vAMRBBiUUSsmQEm4P0yX6b36cieSZZk6Niw1g1N0ctwPvlfX5zpV/USpPOT+5nhDR+Pxv/fsGvn69D+5kwGFgrJkQJwRMbYTD2O8GDLVJEjaCQK/fi/36bBKon61r/W62a/LheqDcyz7hieADy6r6S7DEWJr5jjz02fZ+aaUFmBxDvCWhWCglxQqCM2UYeVszO57zIERXARMsdxCXOLSsZy7yAIDVL6KoJit8jVtpPmIAg7OoixdW/Ge1/x+QiZgwZTkYUQeU+tvOQTD9P/yPEEjyOP/74FEaDAPk+1xEXKfLMyEggESMIk3bvebTrz58j74i0kBm2A04IW/68nVcE2PEvvvjiNP7FQFJkvSIF2pexRTiMqcq+10g/iu/8LwIWShYQyLT+RmGHJUzZV1yAi9IcrI21NzJY+cgET8kobWOs5HAGRK6WnUHakEbHdG5zQK3vOo5Fj/qRFjX6GgIptMwckN83R+k3rr1ZDkA4MC9ZOI1mXxzbODNu8Q7zoUWKMJF+6otTkTyNjXlTxTSmQdYsSLUaqFPva3gD3cpaXIdJWB0r8R5I6khsvFPXUtZxYe6+DAAdTWetfnrfvZGQfbff26kZbPL9c8db1TPgCIJYKJOBAWxlOAj3bIcLBpqLmdJhEhxUkoe0wZxLA9EWQ4VYcdNZPVtZc8dy7TC8+qwYnDwuKXfw0Ge1X46pNd8IxlZUt9bDpInYmUCNd7+VCYdwytrUL5wLybGiR3S4ftolO37vWHl+cS8UDcam3WObXy1WqG9UAaqY2CRGSqC3rF7nVZdO2ZZcvoWxpWpn0ofk+Q0Vg1qJPDp2u9fXCEGjnjJuSJ5wBPiXRfJcf1b4LPQs3hFZeCAR3IAyNCXM5FguSkpecNTqS/H+1AhYNBmTFg/IHNLCvnDPWszw7iHaSlTpdzwSvp8f5jMZ0oiiOc5Y1p+pciOpd5W2wHnM5/k3/q/8vPJvc49Fo/6tvfV348QiCLH0iuyZn8wl5iO2sfIYo/2NpLkWCyzXMpqNcX/mIwq28en+EVDnzYpoxqlXr1ORPFIr9k0RM3mbLEe7ydFA68bnOhyFRJFkao+YQnE4efBnqbgfyRB8PV1bJnU6stWNSU2HsUq3arfi9yoORue2kmEkTIQ6GqOqYzoOTPrxfuv1h4yDe0AG3KfFhuw99fC44Qwmg3cQ+qV75eqQrYWgijfSF/s1dqPRSQiB00YKBFO1JDKoVchtxwArb8P4Ww3LXOXKM594T7txryBpVD3xtFzwFCmfVT6ymmDxidwZFwgNJcdvGCQEGrEQg1cWsUEutFsmGNRK6qB5RX9kwBDIRkjQaN9xrny+fE73gUSaAxg0hofCgMAxpOZl44BxdO/GCTc48qevIdPmDscd7fztfu4aEOxOKHkjXRuMqLP6kr4gKxoJkfhhMWhRaP6z0GDPQuGrHFG1/0aM2QyKutJU5lp2x/iCLVKlrSlWFhxU9Dw+hUsYE5RAIpE2YosamevNhwQZaqG+ru3q/c5n5gnX6hzmEgtn9p/NsBighCN9Fk+jXUf1ubKSx742QvLy9RBcXAP8zE9stXPrg71W9d5F8qwIqWEmbStLRKEaiH77X6PrHCYFbhqTP6KKHIjLUfdGJ2Uk+knZy9dNotZRXaOJizJiMIkxZEBlPLsXsZJes4vL4GNErR4MPPfJ/aOjiwUzgNzvILUh9Y6Bcj8MuXv2ysXH6A0SwTNOxBkhd9qQAdZPez3oa0/1jX2S3aU5Hg7h0W8pa8abvVgFzlMvZ5pppmK66aZL41FIBXebV/OLDFd9XX9F4ioVThiZILmFGHXuXTsr2NcSsTSJIjvIkPMjZO2Smky2KHdII6XAfEgxM9aMO9crPpQhG4mEtPuea6h8Ok9+usfRnvBABmHW7rU08nsuU+2B5OVQmUy2222PWueHBxycx32aL/KOCeZLcyJV1/mREYrKoI+5xkZm69+CD6I3adKkhCelXp9XTo3NEZ5hTCN/yAxMfZ/ah6TBnEBEbDDHjWZzkDRzvb6qpI4nGzja7zL3YDs9fd/T8Zw3P9k919Lo8fJxiSbsqQVqM0pgtuXOaZErQYvIRP00T/ay/01F8jScScJkZoK2QmwWpAxWL141MFBNzFaXyAHCKlDaBGSFa1JieJEg++P5jQ7iPjVUGddd2QEd21On02l0Auc2AVm5kJapGFZMJkuDycBCCqiS3EMGG8LHeHo12LjK3Jd20l4UEbFNPnevgpYVI7XSpwRY5Ti31YV7LvN+W8EsD1DXoh3I61wDVkLcAZQv6p2/uQ/g5btltVEr19zKbxgh4QPah9Kc411an47765eZ8FH3uGwYCe2JKJnktOGMM86YFDDEjDpglUwds+hC7vJq10SI6EnmsPCh1iB3DAglkOERt4PcGcPtEC39ye8dRxuZ3M0N3IGyoRFy40iMH3cw96Aga+7UTGJqkZBev+/ePDt9Hc5hrqVumoNghRCbzxhJngZtiMTrD3CDeZnX5liO6fjmDwtdqpD+Yu4wn1g860/UvSB8tecP4894FptvHBsX3OFskhhQyhh1y3hFXMzFxjNFXlgB28vW1Zqj2Ry/Z/+Mf21D/Wf3EMWy53fXUetaas3lFHJZ+JJAMldQZSTbzFq/y+87n+/zcojtY9ctSMyNvSJ6U5E8zFwjLLLIIsk1gZm7uXwDg/LqHkwoSCqgESXKHvJEiraNiolc0KYJyERhVYEAtUtqNTLMGDorE+Qqr64NElKyzi2ORQdfaaWVEjnjClKGAPYmTf59JE3n19msVhUU9Wry5MY1mSKu+Vhc1GLXHEfyDKJE/WCsdDYD0kTIsBmQzaxUym57kwHSCRuKMQIkviqrlogt95N7Jsk3O1jLvt5Wj0cRsgUfkselhtQM68Mklp/mEq4PLhxqLIPLEDMg+Tv5NePBeBg7XG4WKRYz1D6ES4yMRVG7JCGTAv0OsTO+jCFqq2tFDrxyA1KPKZQWYmWcu9Okq9vHhyUSx8Crlyeb0pyGlCN85jHxTeYeyhrDh3B1guy599y2+h2yvs8++6SFsTmQymyeMS/nRUXud/H6bgSMTSo60mxMWIRn17dX87HFt3HNDiE2o9lORNt8aCHgdxZtbLSKA+xBq3Nsmb9zLUKizAe8EkIAEFxeJNffiB3KHIAnwO+plBRLC2G4dvsxFcnTeAKnTXLcLFxmXH6N3FiZQLd7LNebSQQSpyORme04QO1C9pAhg9++iyYDwdQmdCtTk7rJS4c0uTMIXEIMjCdm7n8NTyUzcVmZIHEmMhOMSU1nZqwQTYaeyiZ+hAInS9QTAUX0KAW2AELEGB/HF7hqUkJaKYH56X8dDklSoBFp04nERRhw4hGsZgUmc285D8WPi8zkmw2YQcq9iziK9XE/OrnzIlZIb+W5GWC4ehrQ+Qnvymd+3/f8xnU7lus1ETsXnBBtg4BCiZBy+YjfggUyzBi4z9Emj3b7S6d+DxMrQ+3r/kweAsPHwsNkxpVjLFh8GHOKWBtLucyA72TlQD8xfowX/VYQv9U01c/4ake50+eMJ2PZODUfICVW7MYl1wrlH9kTYI4MUAuNB+c13h2j2yRqEM4HGxjByhxkUWYOhaOsR+5t8x+MPZWnMM8JkEfmETLkv13yXomVY7km84z+g6w7t34lZozKaH7L5X/Gwnhs5R6NU/ZTAXEqvAUaBQ/5Y9+QIOObmGGuG2ke9b6xTb1jX7W/eUAmrDFJaGAnav1+pGN28j3XyuYa73iAPoyMslO8CK65ETHI/bg3+PEAEGLYdfGL3SZ6U5E8Ey5Jm4o0/fTTp8FJidIInQS2k8dGEHKjUcC4kJAIJHaaaaZJr1Q07gZlLkjTYvoET5qcBFxbBZqsKEuMg0lKw5kwND5jYWVCdeAi5malSDFs4hllZINnAAAgAElEQVSoal65rhAtkw11TcMjOiZFZFGsQ6ukRqfSTu6VSocgmUTVIbOSoJJx8c4555wpe5obG/Fzv4gfl6L7kT1FcUIADUQB8pREkzfCYiIn45tEDQQk0wBGDJ3X394z0fqeidZgoTzK3oIfeZ9Sh3xSWGEvlobi4/rEVZo4Brnf6dP6HuKiTyDz1CgT5Vh5WDQiehYeFjfa2SRvsuO2zi5eRl6/oLLrFxaX3KLtxL7pm/qgceA4+rC4Lcae0bLgstgxPoQ05Pi+IHNPl0Jm4cggmtcE7JtHYM3Am/+0gUU3cm2usahGFLVXmaRaH0Dutb+kIOfUF3lzzI/6J+LC9nXb+Pb7PAATdoX9Yw/N+eZkBJ5ayz7UE4H8lkigPdk6YQ+KCBvv3vd5J21/u8c2f1Mo2Ty8Aaml8LGD7hsWo90D0sgO4g64hEUN8gzbbj2mInk6uQ6PcYuj0ShW0ZSYdgHr5e81hAbRsTSORssETMNxKXil7CFo3J3KOiAdjT5933OGGWYoZp555qTWUSMEcVIKxRZZvZrsEB/ytw6E1FkZ6AyNdJrRcHSvOqfjuV/HR5hMtkiGzqqzIaXcYYgekouIVj7dCyKI+CIpDHB2wSCojDX3DIWUOw3p9aTEuF/kF5mjCufzIHQZTySYG8C1IH9c0wLyuTUZA9iMNoBGw6KXn7t2+FMSqMbwY1SMr7HyMJ8gelzUSJTYG/0N4dVPKGbUMwbfewiAEApGmbFnoFshXX5DMTTOqXbGN0XbU981DpEKk6/vtXOuSgUp/p6aIGoHbcjIwxjWMGfokHhuXKSLZwPxMhdQhsyPZap7rgHhRCK50HhYqMvmevMzo60GJDduPP6BgPELE7aK693YoYoieJILCApszUjzrPfNf5RztoYtFCrkN/jEIMzt2Za6XrxBv9RH9R0Lk1yibaT7z+85ht/rz4guwmwc5LCVf6Ddub/eRfLE0iB2DD7lx6RLdswXPeivQDcZIxlctwgtFyXDwgibZMSYIEPcRRqFwmXFicV7amjqGDJD4RNPxlgZAAgiMuNz7lONm92uyJwGL4PMNdMO7jmTXIPM/TJy3BYIFoWD0SVLM8QGpCxIqqMJmAIJLwSMIonEWgQgbIgg9a3y6T0k2vf9zu8ZWAop1dOqxiCxwhd8T8JGArhtqT0I3yDH4WkbmMOamwMG3IJIx1g0JFatyC08jDeKdx4n+gYjoB+ad1pVcbJyRLUTfgB3QeMWDvqVxYhFDvdJJnVByqYmZd3CQ1tpZ3MjVVefMKcKa6DkmoN4EywC9AlGsVXCX31PzovsUW/N385nAWYR7jwUZmO0m0pL58x7+0eGA+8esobc8LhQ48zb9QieRTrPmTGobbU5+2debMZ29dN3kVbeKt4387k+Y9HSSGy73+rLeAH7x+PVLaI3FcnTJbB3N6IxGWqTJYPbT2C3cy06GYCt4qhUpOe87xzVAck1yGXDGPAah3GCgY4rrswrZq9xHc/vqRXIE+Io/orRoqAZCL5T+Wzn+tv5bb4G1+SJ+HkafIioiZTiZ0AjvNzIVmwmYcTX4NZJkZZZZ501GWvqC+LL9eVJ3cvkF3mkyomvM+DFOHLlugdGH94mEa9W2CZb2HHvUSBdbzv328vfwtdEaCJAjCkG+ofsvrH40MbIvD5g0STBiNGwMEL2KS0MQbVRbuR/v2OgkTtJTVQH6rMQBX1QX/Z5JpCtnqeRa4nvNE4ctYM5x5Mr0ByA3PEAUP+RPl4CRaGpKPpIGfjm8yJ7FrrmrByvbIFpjuJSYwvH+gMG5ixtxMVN1KgXwmXONncTh8S7E0oogTxLgzyfsyWu37yOE1CiCRa8VwSK0YQwv2Vr9XGeBXaBzcU3Ov14F8lzQjchbo0iJT5vELY3a8agI2kIBaUJcRGXUf3QuRGQTEIYqZGe+TtICzmaMkH9Mnkggs1cV6++qwPmDmwwelIc9QMEEMlFbvUDCiDsuHj1DcbToEdgPA1oJBrBMdjdk82qxV8hzzo1zConULgik1x2SDKXtvO7pl5h0u55DWh4ITSSSSjC8OjGoK7uy738XztbsepDjLV5RViEhQHV3KIik69mDThjTZXTJxln5IACzbhQ4i0srLTLIgfNXl98vznCl9U9pF+SksUidy7l12LS4o9rNccDt4tvJpcWtRaxjDZyKRQlz9+9yojs5ZitPLf5ij1gJ3l6qFG1CJv5mr2w+w1CiOBp01rfb3eO7dXvET223aIyu2AtQrLoU++6zIM8fOYqmcvw6vTCf0SSR8GyAqZAiKkyqAbZ4FaDDmhJFVyMpGQEBvFo5yFTi2rFDcUFgN1rwOpzD/L/Ojd1UgcVs6eDI2PtEBckwEQqToabl5E26TrXIGNlYjPBITVIni13FGZtt5+100e7/Vv3iuAhYpKVuOy5ToU2MOTwacVQZyWGu0+WNiVGAhFlUJyXIHuftXLs+E3jxKyTWOkbYveUuKHmmVMRMGEzCJj29R19od3ryIsFCWI5Xk+MINXKIoG70kK0cmHa7bHUi/O5X+q7NjCPcZ/nhftIc7M5D3FGlhF0uHpvpO8O+nv4ENvHVpl/2EKhIqMRWr+DIUxVwCBuyFbuZN8akeTp1NQU2Y/cZ+ImBt3oVnYqjFsGJ7cjVYoLqd0imQidRhPLqFYURYuaU3neQf87d1ATITJrASCWkWuj1QeCSFnlzkSGDBiLikHHygSA6MskpBhTJrj0xwLJM2G5T4tFhEtmXg5yZ6BNhu24Z/1WfGOu4eXY1BdJLoiBzxmbdo1//L53hC8TeXOB+Vl2PjUPmUf2xDVxffEklNFOzqff6JtcccikmHRJBspamY94IjppjFudQzv1O/M6TCTcKSVCHKnFA9gGngtZ8sY7HNk/7w/6XF7r+t0bLmGeR2x5tiw8RiO2MGTzhMJx3SKKRKJO2YYRSR7XoxUMVUW2qJgqJGZYGowbErBWhxQpxQ7F1VmtNfsw6BEVcT9Wf9RP0vagJw6M1LG1vw5sxUuV4ZaWqcjd3erkZ0EhfkOGJRcwMqQw9UjnH6T39DGrNfclPsw9joU4H/2AMdRPxLtS18TfiV3hVqXqtWqUsyE2dpX6gavYYW4hbryylJ1Wry9+1xlSqN21LWKvPpsELgKEighsU7uLhsp2y+fiflM7Vf8VQkKJFkPFGLfjuWjWvvTq+wgHAkNFtQBH4GrZ/0x2LODYVGESfjtI83Wr15ptIhesGGBhI0qh1cIqnwfRE+Yk4REx9hu8qxOPEUmeToy186vbd5L0yqVZi8XnCx+U1xwvRWLNG2uT/1sBGVYIMIzEMJoUGKHR2PygYFV9nTqvwGR9QyasVZsA5lZWuSaSHLfGVSv2xkROBas+76D9b5ITF8ZAWAnL6mxXLe7EBFDmMTPB49KXcU51sVCkuLUTe5eNMFVBHIyxphQL168QCWpyELzOEKyMfa9fka8cQ2eRae4Ww4tUIPziwMrqA/lc5jUZ2WqIStLjuUBgzEWdUl3KHI+tHss4tvi2SJXEJA6v3pzM1mkbZJCLmztyWLhCI3aHTcQBLGp58WwwAIPRiB4hwOJU3LZ5DC9pVSyp19YjkjwdWHYpRYoLDXHRiMNCXHKjcElTWpAV8j8JFdFrBGjfofw5lsaVnSXGz+pPdvJoDdxI5+nX71gAmAC4umEnfhN2zRA95FinpgRSBdWS4xKwWh70CULbw0OtQCEBXImSUYbZMBgLVA6LJQZYmyo8rFQOgtuu+5QCqCA3lx31zoJABnsmj70mIXH+7pBMBAzZRzyUslDLlVtVvxCfyX3rO2W1h+MhlciLhCELC0ka5qlhTcoQRwtDmNra1IK1nj0z10mKEattPA4LT2jG/rJZ+oSYYG5bcx4SV+8YfsPjJyGNrRB+0Am37YgkDytEYsQmiHdBXvyNrda76EH7TDaoVaCMWPI/xUGHRUBGI3oMti3gTCwGvhg1LJ6be9g7OXJGaiYzizczyZr4rF5GI3pwhR0XrzgbMWvctDK3uF2GATuDF6kRz6NfUbWMnWF9aFMrf/FwVA/3rD6WhUAZmZAMjsx1ro0cRyuehUEpy5jHcbpD0srCWZ+woGAguW3ZKV4FcZll9LnK63QuRtuiwnwlTEBfpByONt8N2pg3ltlx8zmFiUpeb05G/rSD+dsiXdbpoC/SW+UxSJ15CjkWVkDsaeRYbIWQE0ITty3+UeajJslzEifnZ1b0lotEA9Zj9I3cUD99R6MYvFg0dyHXmq1vqAYIHLARkkz4vFIsrHQwcPEgXHHctFaUCmxSuYYJo5Hay/2R70nNspSpedQVWZOwUzKFazJjB7eMnbg07jy19+x4wWhzg8jcqhfYO9J19Ot7sOHWEaPJpaRUiMzaYXwYDwieyU0GHkVWvURjgbuLgaw0mM3+bQ5C/iX7GJ+5nxm3jGyzx4vvDxaZq9de+pZFNY8MV6HFuoUVz0rZRC/3Q+5b5xJnKtheUiL1xTgY9Ic52rwNUwkBEk7qzcnsAAJI6CBwCFMiAAy7/atld5BbpcMsBlTt0DfgMxoeBADzJ8x5PsquwlCX5MmOEzBNaaHW1CuCWOvG+/n93EkBbMAiawhLztQzwUhv5ro2kCdNmpSSAsiqRxxxRDI4Ei3EHUmFHqa4xUbaDelnzN2/vY4Vz2bgxSRk7BAAT9hZ2YipsjcpYy3pBTmGnWSL0QZDI9fU6++4B4omVxICa49UriX9Z9geSLy2lf1okqfqWjBpYy61dgmePsRYUwSp5fqLxSZjUsax6xGI+GwwyKB+gOybh7gLzeF27MmKXpnt6Fz6tSB7ylWOC/U/G5EXtYM6zl2/BEQk2eKdildvTkZq2ACVKlRFQIR7Pf/2+vzwQu7gR8hoRNn0G0QPjhbKSHYr+QG1+l1dkkex4lLTmZUGsWIatqwZAFP0GGKxRFZolEvyv6KqJFRV2EnRqvNLOCDX+w6jZgsepKZyd4ted7RunR9uDLxJddppp027YOgn1BxGP2OH8HBZWgFbLFg0IEBce/oUcmwF2K3r7uR59CfJJFZySAnDo29YIQ/Tw6rfREStM04EpiP44pfKIngMtAWYLcksvuyAIIPP8cs03nGswSB09dqJB4E3wBZ55mXGUohRWckY+dyInnPJFBd7xTYq6XLFFVck788gK3pcz8aWXY1UnEBQ6s2VVCrfJwSxkVSset8fK5+Z7+UzEDMaDUFCmPVVdkNcP+zLetQledyVggmpEbaxMtk26mcepAZlmLnYDF5Sq3giiRTkfxMGQkKlkoSipIy/xWaI51PUVYMMC0lptN1gpi/ICqLKWUEjwAw+EpyxE5/lyUh79V0hALZ1ociIgXSsRs/b799zLwyAe6Tycv+7ZqvkYXlkgsfgUTS0tRqRjGrZdcuEREj80nfypOm82ejG6+ATtDLaUJ+g+gqNMDebs7PqW7Zb37moVsa5xauFqwUI9yY70EhMd7/NBca0Op7wazQ+2iIfBmoKEoOGTQBq1dbARUk1OMKFSjeajfO57/k+ty1eUVZiT12Sp+HFUFG4EBzZlKTI0S64VXB6/Tv3hbAJIGdcuGQBLkvQIKZATTPNNOl/+7rKmBxr5E4bwUlHVug2kxlBz4pCeprsBJKSrL0PP+5wKz7ZtDqwxcMwYueeZJrJLqVuUZ64ao2lYXkwYlarVvwInjILXO4WSWURMEZUYoWFlEWV8WdMhooXpK4WKdT3uLp4DsRvIl/2MvZerd+0877z8WSoLrDUUkulkkFcnUJTBm1R53rF31HjKUlEj9HsPFJnYWeLQgt2v+m1De+H81PleHMsMogZeMJoWGa76ndqE2oDpK8MZbguyWOUTOi33nprWhlRYyg3DHwjF90PgDd7DRqIDC2xQvatuASuXMVsx40bl9zWyq4YzJQs3232HIP8fe0u5gxRMyFIWFFaQNwUVU7f8GryhJ26d54MNsMt9s534DzIOIx07e6J61m5BdnW9t2EQRkDtV8IIrLKGJiEuKqQL6SWW6IsgqfvUF8YDgqhBaZX/5etyrRj5OO3/Uc4zTFq5iEeFiDGoHg9/abM/pnb3nEJH7YtlGhlPLANtgMblHFvTIspNL5kKsOvEftuHrDwgrUM27FmC0eyAd6DHSzE2BGJzI2NChqIMzXPXudsrHZp9zEqycPwXaAAeYWDxVUphtvoRdcCYpDe12hYtdg7AeBck1xI0velPGvQRgbFIN1z9bW6PyRGJxQnheBxoTH0VstwGEt9ohof/+sHsj7FIyImyB7COywPcwGXjvgjhY7FrcqoLpvgMaAUOzFWstfFv4p/ch5GPBvYeO0/ktUPbYJwIB8SwpT/4uYvI9O71r0hjyoN8PyI6SYCsBWSkgZBwXeNVDiuZyFZVPqR5rfq9yxo7fBAscIJhnHhXn3Pjf7PXpq/eLHEKRM2GvktG2Lu4wljV/3fbh8aleQ5Ad/whRdemOLyyNJWRmPN/67RdGrEDsFjxLnkNIQ4JHgMM9HT2bhYrTKs9iQVSLAwsXHT+XyY77+RAUrhVGLBit5CAFZW9MPyMA8gsdyz4g3VCuOe7wTxyvFVueC2EiqdNNS1DHi8P3hEUn/UL9V500+ValLmoxP9NPcPhtk5LUZ4vPRbHrBGi+v3co6gOCKqhBzzF0GjkfkOGbTIQ6IlXQTJ++MU3NhCdlGYkiQWtrMRTP2OHbGQVm/PwrbdWoyjkjydj8uWm01APfcclsl3PNaMOqUK0bvkkkuSG8AqUeyH2CSxCUrMaCDfG3RsXL9BawViMHNJcNEhuFyR+oJsY4a30UmhkU4+yN959tln02o4l05B/ochq9ZCjyHQ9+3hScFbb7310mKPceuEGwzJ4wa2bRW3m8r7FJpOnCsb6ngdPEI3UpvpIwysfbAtxOedd960E4E+1an+47hIJNWGi45toOgL1xDX3q8PY5viKNxGjcFGy6SxD8KVJJaZE4Ytga5dOwQfmCD9hBBu/UaP6bdCnJA8iTCEgnZiPBsieTooNw33U14ZkafHInPXAGIRFLs1mBk8qpZYDI1p6yXGHjny3UYbtt++h6hanUlCsbuAUjHIC4Ine00Wso4bCt7/rt60tUwz8ryFkIlPH2hncPaLYXAPDAFlUnFnmed2h+kk6UKQGWkkT0gAkue9ThnpkchCvDfYpE/9OqVUuPslgLFZnVTz9BfkkptOQpr5kgAglKVf5wHXpRasclfcro0u2M13lSRPDPsg27uy7S8sCD5Kr+kDYtKbOQcRjZcQiYYzoa3VR8MkT808RkwsDlJj2xMNOxaJnnvmnpWQQd0SN0RtkE1pNUTpVP9NVldlokG/DgLX5Z4QNgSWIVXwWeAouZlqJ/6OG1LMhiQUGUORTfUPgmdAC7gWk0M90P7DklVLjRRzo0SOTFeB1voHkt8pIhTu2sEmWJ3qF80cd8KECWnhzV6pZScDnPLczDGa/a65k3fDXCB+m6fHgsgc246hbtXAj/Y77mSEwgYA4hibmdPDXfsP9+xIBA5h1ufY0Garkvit6hVCDqjDXLatPhomeTqoDsDI291APTQTMWIw0g2OhfcQI2RHY8iGMZEos8IQyjhVP4jLSdaSyQKBgpffeRr43SZ++ZxeXQPFjuJktSDeSsAwRRJZpaC4H7F3ivq6F22uA3b7uvu5P8GQm0MfgJdBrb37cVJvdqLgzuFuUvoGeUX0cz/opKrGGIv9lR0JU3E/XF+dVmKaNerx/f4lo5RmfZWybhGuYC81uNNtpo9SbsSROq+YQPF5/bjo46GzQ43sdeS0GXvO06PahhJr1Er2pJ/n6W5fG76EoOFKMG4GHzZFPxL3TGxRlsdc3MqjYZLnBNQ8AaxiHBQJFptGweg2eP10Po1B1dPJGSWNstpqqyXli2tbEK5BjhxzcSKEgikFYiJLOoJjZPLVqXvLpM4gRurEV1FipGnz+6tHxqWx0EILpXgSblkG3QrPfnoMrBgDvw+CN/UKTjty03NjS7jIg7JfXTTNTBSIqpW+iYr7abfddksqXicJHiOsb8riFiYgq5+KSDnvpHrYaeMfx+8uIbRQEGJgcWIu5pI0j3W6HYwN/ZRhVyuUF8QimedLbGurxrqZcdvod1966aUUjqM2W7O1S4kWOABln5uaHeuU/RrE47KVYuvYVTH7zRBoNpadpgJz95qDWxUNGiZ5udNQrrB+Eri4g0YDNQexkZq5ZiwdYeOeVe1aOrrGFcNkgoEXYizrSiyfApoylhFDWVkmJGoaIqUgswGEPCIQGtuxPXUUTwMq/+3VZ77n+36HfDuOicU1aSerSysLErKCoWIwtCE3M7XEE4FHUnUsRY1dl+PFAJ6a2OW+YTAizOpkUTy1L3LSbkZUHm+9fGWMqA/6gT4iVEOf7VRx2UrjaxWr0KxFk/Fj6zwFyPXHyu+V8Tej7HyOXe/JcHea3JZxP/18jEax1h7tYq29xMflfY+5viwUuoWPccJtq5QLRe+cc85Jsa39tPhjLw499NCkcrIXzahN7ALPj31r4coG5Xmx3itbku1Zfm3mvPWO3anPzPPV1+3/etftc54vCTj2UoZ1MwKJ7wqN4hkSKkdka+XRNMnLW58waAJaMXmdo1PgDtJxNYpGR7pgQrGTCs39aas09ZOs6qg9sOPWpZYhWlZ8DBqJ32SgVAujRubXwFYEjqfTMEQmME8rKDK7BAlkkaKEOMqWosAJWD/ssMOSAkONMeFkUod4/v/27gRolqq6A3jiBohItDSh4opLABEjKEpAJAHELcZyjRbyojFRRAyiljwlQQwaFSVlxCguqUQtV0yMiWtSScVUZamK0ahxza5GkQfCk+Cunfpd60C/eTPfNz3T3dPTc6aq38ybr6f79rn3nvM//3PuuUIZsdUY0IdtxO4BnECjgeq5mgzOdeqzZduqv7EDJ510UmG6hGyBviEp8kUUg98AeUIy0g6MFWyEQqnGXdeGkoE31uX+YpflOkpE9l1b93YPzyKsJ2fGXAMKHBh3R/zf35zDcPvNsgCkrWdYl+uErOkqCyA4wiFbi9imydq5y4A9/eQ+5qbxa5upSJ3pQ27aTm9jyehZudueaVFGZtF5POt3WEXOP5AGhND3TfQ80II0wO7rQ7/fTp/Sl4gi9gowdPjsu60A03bX7fLv2oV0YWu1V66nfjW+fD9LZn5nDFj8I98R8TLr3Gntdy7dpH9e9apXVVjXRV6NQZ4kbMyQ3R/UigNQgI+hdtA04fXxnQ4CkEwEVCsAZiJh0AABHQ9wWdQAMGPQhMN4fNg/qwp5oHLj1KXjDQCKWFQhVKDQu+LUj3jEI8r1MIf6Q9gQo+TaVv8Clq4N3MW1nXfqqaeWbVd4m0ILwCPmj3elP5sMyD5kOrR7kI9JLl+NnPWZbcy+/vWvLzIXB/cbRoCRNJakHXBAgJy+AI778GTV5WMkhWwBLYpzGSPt93KzGHxMhHQFc9NiGfcDODy3g/Hynb85x7n62G8pYNfqSx7LPPOqfks+gA15kRund5asyZ2s9Yl6bSFroFB/Ne13RhgIOeWUU4pTLYLCge1LFsYFnSpyQpfTw9JirrzyypU7gRw40QaghQ1ZpFoGOwGgSUXaLnWLrsT8wQr62GFuxfzyf39rynZ1aRO0GWHDfhtH2sgx0WZEihCs8eTvzptsCxsKREs5EQ1ZBOSJ7In6IWoQL4uE+huDPJYI0NOpBq3cLQmtTR9gUiCb8P8ABbZLMzmwAzpfQUnJq5gSieYWcABoGAyLHwA0Ro6ssYCOCK/6LJylLpNwMLAINAJzWELKRVkP3gAFoxyKvEqTmmcCsAOjmyD/tp+R3Bgw/aY/gBATfpmVUENBepSJLXU4Jcae+oi80b4BDSNk3BrXwsXmi3G7qKHWfswrAHHuueeW6wGO5gFwPo1lAXbVqsLQao/fArxC1+ZxU/CxaNvX7XfkYjEXW3HeeeeV6AT5kePVV189VdbkT9ZWbnKM/VYqhH53rSbjD8ijY4PJs0uPVIq+5eg5hETpavnZ0mZWrSPMb8XNARbgl/PWVD/Sf8qFiVQBIvps1jWcC6ibM4BvLEIR8VCeyZy2SIbjNBTCSDtEMjgdSBAA1PgMgMzBV6aHc0J/sO/15/d74xWhIzK3CEZyT/oGIUNv9Qby3Ajjg1nC5gEm6Mt56Nq6EDbxs4FgwEP+OhBSR1UDfkJRvBleL4+B1yvkKpEfEFQzh8FTogWyd5hg8v8YHWBbuJVCjIGpX4JxsDjEoDXYeGHaYSBODs5N7Jemz0xmPFOhdYBaqQQKbAheehtAEbBhjIVqDzzwwMIc82b7NpCUPwaIjhFywxow1E2MfbQZ6GDMJDObQ8CdfmTsKO+tQuz+5hx5MZdffnmZp+Yc8MKIL9KeaNcY38laTiXdRWcBd+RGfiHraQbLdyFr/SJEFaVQrORsAqqBPAZYjrGxo7isvupb3vS6May+JIed42S15Cpf5AxoYUx37NhRQNYiOhDQsbUZEkGfT7sGG8POASvsnDGgj7Uh+tt3+oXNc67fTLtWn9+xj3QNR0EtQeSW9np5N461E8vPbju/bkv9Td8DedKnFmEp4QTpWvLytKPehnnHz0JMnoubgG6KPXJA8sBK/SH77JCx3Iv8DA6dCzQbGECZyRQLKQDsycPfnAN4+E2AuOyP6Qsmlh0v+odnKm0Bi2ciAyTAUSiCeSfhEM/DNFBcFjxw5Oxugknp20AyHDxYTAhGEcMtPE7WTYEVo8+oSXkQeqHDtgJ2s/rFb5SVwYYzkNimRdrTtyz7vB9Zkwt2m3OArVnkZS5h/Ti9cob1H1nP8ywYI3nNIhrm6BlnnFHG9Dy/bfMcYxi4NFa0A/Ovbat8GcPy6zmmokiet6lOZFvYGQCW/gPAp9kb4Ac2ANJngRT97G8Ao3P9pml72j6fjufEI0bo9Wkv4BQIowvY3/rzewY6Uy68cUhWTdsIC6hRKnj4KNkAACAASURBVJ9UXh6Wu6l9WRjkGSTCG2hENLRwDurXg9QftOlD5fk/AiVkGIeOnveI32QfdAPuYnxiuYANIXX5aiYgb28sLwBIKAKoskBImL/NRQ9NjCgjKcVA2gEjyasFHBjKJtcBDjBLWAfAkQ5rqjD1r9/4rZIT8mstCHG9pqCzSdvX7VxjhVzYB0ZqmfAkQ2oMKIFiBwGynkcenDD5xuan1CKF6303z2/bPMe4IA/6ApOnpItIyyodQuMXmwhU2Z1HlCd0W5N3dgnTKu8sgMyk7QGW5KYJx7rvrJe/OUcIeAggTxsAU8TJLD1hXNMrFjwKV9efHRbyPZCHECOrJrJ1ruu5v0WZ5pM2bSXDabJdGOS5mAeEVCVmC+loiMmhU5s+TJ7fLShJ+bYjX5PORBPqs+BFPqRFMca96vFjeQk7M5AWlMiFE0ZpCqraNJRyH620ZSAB63POOacYlybASvvlFfKKLarALs3y0LfqR0oWkyccqSyH7deAhyZtaVM2Q7wWWTPYQJ70E/mdswzlLFkHmMbkMZb2AZWKMi9QM0cBQ6FaJAQWcFVjGLMpWR8zLrdanuGuXbsaG+xZsmr6vXFPj6m+IO2Aw7KojQAQFSsXluf8ToIZ95GrLJUIZpgGUnznb84ZEpOnPfLtZgFyOl8qgjEuulYHeSJqQtQiB5EasoiMXUf+sLQsoeymOmspkKdjTEC5YEqCUMCUKNpykYfJ37QDRFKO3cmRAqPI5NVY4CIXT1LtIjR6U8Xc5/kcNZ6jBQ9WawtvMlSrAhQAlPxSoSWrxDmWQEQTcBXXkFoivxUjRH9NMzqzZO1cAA9YwAwJY1thlwBvz0LHmDdhLGCGrPUTuTWRNWMGiMsplnssL5lBde3txqFzFEKWy8kRU40AKF9VP2kPxks5FekP2gPMCFGu4iWfTIoPgCdHVUhyUbsB3LD7cvT18yTJQ2cCSsL33qc9s+8wYUC8tkwCxUXbtszvPIfopPkttD1t7MozFWVAdjk/QJ53OIiuwfYvsrAl2i5tCwsMSAPU+q7JaymQx9NyQxMHJWkyWa7ugeoPHI3N9+7AR8q2H9mizk165WqkKViYwEttOvGaTNJVnMsAWJwgvCRMKjw6j3Hdzvgu83fAitLFoArByW0CPpuEkQFVXjWWEoshIVoyOFYF2yRMzTtndBw++87fnCP0qAQIwIHBk5g9b47YMs++br9lE/SXXKWo1wl0mStY4pA19maarC240C/Kj2AxAHr9pv+2A2rGKYdAHqfxqz6p36+KxdN32gyscg6lHBx77LEFGKyK/SdzgIuTIhUDQ7SoDRGWBO7k5ZkTkwswAR7fAUIiAkAc8O7ZHT77zt+cM5SUL0ATEDdujSeAji4wZjks5GX+00GY0AB4vvdZv1vRDUQvGg53LbLDQnNwjWH3b/JaCuTFjXjDGoHJE7YVSoHKh4DGFx24+bt+QNM6ydnEZeTR5sKYhx12WFm9F+UAYj6M4Z0BkH5hURUwRZmtGuQxlAAd1uC+971vKS9kxWQY/3mBkOsI/773ve8t4RSALcp0CLtQpMCIwzMDKgyQlbTOxTYoCp15eHuyd9PkT36cfvICrAE2B3mSq78zpGQNwJE/ZpycMaX6mlMFIG0H7gJMuZ8+Uj5KPin2DHhY5fjVduOKDEQA5LoK3wI4q3gBeeTOkQOAOXWL6mJ60e+FazmEmL1ptt8CQv0r7UKNOSDe4bPcQH9zzqLtaPt3ngtZZVwZk5hI4whgw8pyXuRWyjd0Xv3+nt9iIfKQ24wcqP+9yWeg1zWAPGw0oNnk1QrIw2J4SDkTvBQhHg8vlkxQTR4oz01wNcQxYBzzqCjmo446qjAEmAKUfNMciSYTdFXnctKsZgTy5JRQwKs0kgEgGEurfq16U3wao6eUEE+7SftcB6hwML7Ao2fE0mEjGB1J1xQ5BxYgBDSc6/C7JveL9m/ie8g65Ib14TSQK/mStcNn8tcPk7J2je1k5xz3UDZFnqyxq5C8vtNf2/2+679rA7so1UBe6UUXXbSyUipAHrBi7gCey6ZYsf+AvDkJkNCVk3oc8HGee1ltDDQ5ACbgzt+mgcPJ6/T5f3pfmwAt40toFihmBzj8nlPOYR3nhK3gzGDyOJTOWbTd7s0h4qwYy1jwJq9WQF4kyMqXkAOBzTv55JPLkmpAb9GHy98l4BvKGKCAGJAdO3aUxGnjW84RFm+MLyBPLglDKTw6BCYvjDBjyaPFvmFTbXkm7wujt2jolAIH2vSxawB9cfjO3+YBGtHGfJ/N8tVlHTKO90VlrX9cw4Ka0047raymtcgBYwhUDqE/tBEAtduQIvfGL0CwiheQhz0F8pRRWYbJo6M9B2aQY0hH+jxLdwfYA5AcQwR309oOqGkvTAN4eY46uIvf+Bv9ZIEXZ1QO97Tz4vzt3slHAW2RFeyg/O8mr1ZAXtxQ2BZNbmsu+XlWNhnYyzzgdgLIvycQ7HoMGL8mqvINAAUFjXlw3zGyeOazHB2lFTBlcm2sbjSXh2AstQFQwAZIHFeM2iH0xNNdtp2uXT+G8sxjbEddzj4v+oyYP+yKrR7NT/vEKmsE4C1z3UXbM+132mHnBCyjki7mFwO+iheQJ49MiBWjKMS6rB4Ffsw/+YZY2u1YOXp13bBBtHmrdtt+jK1QuJ3jqY+Xka3fG8cipcrUyGlt8moV5AnbQrEYAIVL5egZQJIql6ErlxFQ/jZB4LJjQCiBB055YbaUhcA4SIBtWhaiyeRc5bkUNqZB6oX9kz3/EEJedeOpPUI9VvfLv5LnRPdo67w5XPXr5efZ7NsQZQM0mYdC9UK9FkNZ7c4pkUMlrD8UgEd+2gIEWYVqQYjwG2ZoFS+2miMnf15aAid2WT0J1Mnl5WxhU/XNsgBn2Tb1+XvAj95UE08RcGFd8tgO7G7XRjKk6xTztgik6W4prYI8g9XgkUxple3NbnazUhfIyjyGciv0u92D5t8TrPU9BoxXE5SxoLSsppVPI+dEIfAxv6xutGxfuRI5iKraU9pDM/YMp/4RcjrhhBOqu971riW8rL28X6zekAz90OS3ju3Rn/pV/2LGsFHGqDw37AmQL+Q+tH7XHnlrAfKE31YJ8tzb4haLXKRntKFfXVP+GEYVeETwbILd94zAmJQBpU4AeAuAlgV4+sR16d7BgDy1ZKz+MJh51sK2NkCO5MNN6PA2JkteY/WgFvsspEERWhGHxVN2w/ecmTG/5Bpa9SY8Lf3CYoRF8926BhIMPv2ivfJg9NV97nOfUrpAbsxQ2921XMZ4fUAJuBOqt0pTfhv27gEPeEBhTmytNUSApy+M0wjXYsilMzHgq3ix00qC2AFGXp78vDZsDlAj9Gsxh7xlzyu6N2a7HwBPHqLFeBZbwD8WmLTx3MaIMQ/krTxcG4NVCEtNKQOIwsWAyJ0Rq86w7erBSxuTeezXMDmFMzBCwrRWjXNWLJcH8MYapo05LBQtDObZLaSyUmze7aRWAS4YfyENKzMVzr3HPe5RmB2J4DYQlxuD8aMsecVDZvg8i/Z5HoAFO6DdgKw+8BwSsR0++w5rIETtPOf7ncM14llddxV9s+g9Qw76y7MBcHJDMcxCslhbpXQiF9Nze9ZF79f177QNyziEhRdAnhx6YW4pDqJvbel0utOzKvlhRxjj1MIOYKUN0KOdrgNQApDKk7i+kLMDyBQ5FDp1T+e1dd9JGcEz7m+sYpSlDNA32tMGi+d+niEWXhg/K114EQbCO0NI2GhLIA/Yi/y8th5+UuD5/wSQbYwBCoHyABh+6Zd+qeSXAjuAwhhr4tXnbXw2fzllcktU6Beulk/UtSFc9vqMC8CjiC5WDwgQYtePVuAq2UBRyuUDiFYFghiFOLQ5Du0BaABsgIbnrlYcY8xpxirLo1LEVr1GzwSAy0vEbGFc5aMpRaJIKyYlAG4d9Lmf+y8r77Z/X5eJ9pKD/vL8wpt2X1HcWDoQ4sDzBbgb4vPU5aNv5VQZj9jHVZZQ4aSq0WeeKOgOSLehO+MawrbmmPxl+9oqOm6+AV6Lgi56uQ7u5Lth6o1z+W8WO5gHnADjX5oYJ4geW+a+8Uz192gH9k76jv2wLajRFuSAv9fPX+YzWxQlVDCEKymhEoah/m4QYQMIWQ6CsC3vGjOyKXH6ZTo2f7s6wBr0uNyKqJgv/LDKvSbrc6uPzzx9eYfydX7yJ3+y+rmf+7miqIGDuuEa4mfGHkBgABhVRYyf9KQnFaCnOKmSMBgGQEk1eqsw6SXlN5TF8TueczBkGLRgyYIpAyzqh+/jcK7fAJuu4XA9hVSVmXIP4EQ5BO2zvyUjZcW2tmIEsCvCPtqqGLV3eU6+Y1AYZgfwDcximR/96EeXmobqGvoc53v2M888s4BDhhBgUlrEalTAXZvqzxvP6vnIEQBwBCAOgBiAbB5wVT/X713Ltd0jGEpMncLHgK02ArOKXWPthP4AdUCPEWfstNN1hjgGJ9vk+cmQHkF4rLoYMvssrcoY5MgZq23aHEAOODGu6BBjWL6k3TUsTND3QBoiSFgTGwaIxYGJ872/Y+ekzfgNh0VahhxcDo65YOwr22LOOIwZ88S88Bmzb8x4Vs/pWoCY67ufdmLkAnwGmJx8Zxecr02YT9fjaJhr5hdSwDXbJrG0b+XFkLcyOlCnCWn12/77718WYtiaiLDaRLttDtC81uoA1qplb4Ly/Bhbq8Pl4TE26Pex5+FNzmPlYXimnDMlH7BIDOs8Rn3SyK3y/0AFZxOIU+JJ3wolMTwnnXRSYftsYG8Vse8YDmAC2GKgAEHGCRBjpDFrQBIWxDuQhj3zN+cwKH5DXtg2zoL7MUQMknsI67i3e6rnJqcMAOUQM7qMldXN2B7lKLBZAJlctAChDChgFMCRnqVbFdzVRu2QQyqcydgBiu4hXKjEiHcASpuEteVmYQUlzAcjCIQaAwyz+2MU3J88Gcx5AHCAYWMH4NVebWWs9QeGkqy10fOTyeGHH15SJCz8AcjJFjB2v3Ubf8a+NnMCgOxb3OIWJQ0C6F/VtmZBwgBNnALjqgt77Jp0p7FjL+zoX4DdvDBPzB3AHpAxR41hIU9jw9/NIWPA+MXgKnD9yEc+suSoOceYNMfpbQBOSo3xicnD3AN5HB5zzH1FF20vZ+4a1+aQ/gE6tRXABDrrB2DnHq6JMedcHX300aUftVEfd5WKhhWlA+gQjsJKtjWbNA71/zMUYv8EqpaV3CZKzuAizFUb9bz/5gK6yb6nkEx0igGwUSOOwWekvvWtb40+D68+b31mCIQjeMQME4+Vsl4X9iSAJQXu0G59CZwIA/K8VbDHiMk7vPvd714MCpAD7EiMB36MAYaQgQKKGBkGA7vkYHiANn9zTjBpQJRFK0JzdJ66aBwGISXgDThkzDACDBwQg8miGwEpgAgwCDZN+xkaRzxT/N+7vzMCwZD5LVAEDAJWnlcI2L0YVQYS6GBEGT6GSx8LOwGggOBxxx1XDmFS/3cEMPV8VjT7P5l4dsYUaDRmsCmPfexjyzU9v/3NQ26AbYBb8nJ/oBg4BWglsHOw7KCAaQ3WznNHv67Tu/4BpIB36Q9kBJSs0nFkm8lQSBWYBya6AHocZ9e2ghcgM8Y4Mpg4/W7M1MeG+WQuGYf6X7iXswUMGr/AsTFusQjmrM7EuRewhXVzT38nZ/PCHBA23rlzZ3EoXNcYNIa9G/PhbBm3nDJzwmdtifnuu3Di6AYOCyzThezYKM9BXwDFnrnpmGm9hMqkofB/oR+1XShNbB6gR7FStjqoK+FMGvH8fwK6WWOAcjBRGX2hSYrYpKeUdu/ePW1Yj/47IE8OInbKakDsCkYFcFgnA7tVWz0LxgyIZVAobLpKn0twVnhUmF5Jmcsuu6w4pWFIGJN6mMfYco5zgw1WL1QOGccBuwB4AZqMToC1rdrX1d8C9DKWABRdHMwgAMwgGvtAPVAY7KAwGSYDUAVYGWcAWVoDY8gYA8jCWOQKuGFwAGe/lSuFrcGe2FaLASMzchb1Md7I1G+APCATICWrrmTRx3UBcIwoQHzrW9+6yMbqVrZxVS/zW0SN84HZanOxwDQ9a94AelhyzgUgpt/Jwfkxr7z7v34xpqQxSPEyVuJv066/3Xdwhmt4Ts48B1a/RAiYbpPacOSRRxaAh9nGMGPDzV9OknbQB8as/rTi1Vxx3e3uv+jf9ZE5xRkTZm5agL8XkBfGgkfGeN7oRjcqQE8cm5IB9BYVQP4ugVsbY8DE5yUKZxmjcmaE4xj6VSriVRmAuC+v0R6NjLmQLe+W4V9XRmXSoANbogwUO6ACvAjTeG7K1OFz/bBbwLTDOb7H+mLhsFcHHXRQMVTy8BiUYOCGIL9oCwAVhzbGQTb1g66uHwAr4HbEEUeU5wTozMVrr722hCGFIicPoaY4QoZ1WQN57iGsZsEepgRzMwR5TY6def+v7WR14YUXljFmKz7A1dhiG1f54pBIRQC8hDoB7Db06bRrAFlsPQcAo+n/9fkV4yHejUmMnnxZ7WqDDHKNAJNApkObgDSHUDGm0TaOnA5zOcawcattxiu5AZ9AoP7tUm7IB/0DbGp7U3vUK8gjEAWSHSawfAvfUSpdIuFpAy6/S3BoDJg0JpEwmRCCBUL77LNPoe8xLk0n1CoVdhf3ZoQYbeECxkkYW1L8OubmTTPKDAkQwUsG7GOBCeVPuc/b/+TEYAEpQDGWS4kPzI0wE7C0zkBlmux8hwWR83TwwQeXla/CfuYUg7iI7CS0yyHUF2SH+QP61ll2xhiQL4QtiiU87XmG8MJYc24BG46Jcd+lbTQ29ClnmgyMk0mga9yYR5gyKQBW6bYB8OZ5LmBc/h8d53yArv7SVkAPU+88wN3CEM81z/WbnuO6H//4x0vqAzZR6tukvOrtm/a5F5Cn0wwmiZPCtcIivFy0tbwnq9wAva4E1VSwef7mAEDOhfCUpG+rSPfbb79yqKDP+M9rqKZNrrF8R9FRanJ3gGBgWFjTnJ1l/Nfpe0YYWKGHhKQBPeErytUKxK0YFwrXGCEjoSd5V1YRyu+T64PpYjjWGaRs1ZcBYIT8OACKUGM4hMLIjmy2Mkr+zmgKgQmHCZfZuUJelsgP2W11/3X4m2cQFbCQCxsu3G2sDOEFZJnb8uLIu2uyBVjj8GBohUPdbxJIca7MF1EDYUrt68smi+jIVZVPKkcWbqmPX7pAOgcQSA8iBwDjrkCoa2MVOQbaMymrecZQbyDPJFYfSP6GxEVGQrwd0MPo8aR1fteDrK/BkvcZNlA0KY01eUiS65U1sLG5FVPyz3y2+o+hqk/yeSbV2M5hiHnWSm5w0LAscq/kcY0BvHgGgBVjYFWppHhAjyMqN4wil8MTuWNKyzjoNGEaQEPOGqBjMcLxxx9fkqR9hx0BhNYBjCzSxpAdcIvVENYXvsXUkB0GC9MhvAXYhOwYSgaMbITj5DZh7kJ2cmONrzHIDngVnuQgeUYRAsB2CC9zW9+IqMmTl6rQFWAJmyjHjEyMFWFIUYEYH+5tzABQnCUAuc90LvNZrig22RgGzq2sNV7lDvqbsCnd4G/0QpfyIiu5ggAvOS1ii3oBedCvic5DA+qsbhEi4z1b4QL4ofuttgH0ukTGMdDyfdggrMv+MSkpDpPG6i65WFZB+vyyl72slNSQMK+0A8NEEW76i3IxZ81Rq0UlxDPO6x5KqwMbgMXzMDIYOIoVM4XVZZyBP0CODIQoGUWME+cVi+UcxkG+lYUFAMoYQHBdRtM+e056m+G2uI7TLh2HMyDX0cpFRtvfyI5DD/TQ/cC0cyxy8j3HiuM1BpZY3wN0sVqf46h8D4dpEWPdhQ7SDu2xytvKaf3YZX4ZvU7/crDZf9E9heZFCayoloPHkVQuhH7uO7oXbcPUmdMOK+etbBWe5cQZq3SfRRhdykpb3IOuMTd8XmTc9AbyTFyDHF2tflMkOwqJWZ7MyxG65VEYaH2i9y4BRV57eGCSgsES8BSNOav4fDYWfc/4WG3JEBmHnJR8VSV/hkFXo4oRj5DGGNiWAC/BTAF7WAQrYq0upbOEc40JkQiADuNLnwk9UfqAHcPkt2OSSchm2rvntEJZKImR5gDI3WSYGHGJ7BL7GSmGGzAWksXcATzKyACHrkHedL9rjgEcA6qezTxh39g5ixsWCbl1qX/oNwwVh8VKemxe13YrHG0smVp1cljl39kr25hACq0CA7ANgDmn5GlPe1ph8eUjc1CMYfNcKoLzAFDP0ZWsXJtOEfFU+gULvsirN5CHfmdQsXnCGBCwhyAsYRKJn3KiMHpi9SZ9H9RxVx2U1x0euDMpsVHGG2ONvcPiycdjkFDjvCXGCMgLpTyU0MoiE7zN32A0ha8Zbt432WG2yI5xngYC1v27OugD4OglIVjJ6hxS26ZhHrB8gCDZGF/OC7A3BsCiH0MWjCAZYDyxlsCaOnlYD+/YcMbJmAB0nB+y40SRjaMO6tZ9nEy2n6zIwGpt+ZlYTXZviOkf2CG2WB4qcCMXtS/7RScDc+rZAfecAMyZFfxCoaJ6XbN5nt19AE752XQaYC4Fgb1gF+Tq+Rzgrg/5eG7gDjZCQMifXOTVC8jjuUg2Fao14Hk30XEhYIaCYAFBoTKGVv0ZAnZOH0LNewwPmLXZJxSJ2l9AnXGGhcEqKDwbDoV3ys7f7dKCybG6NF/XS0BuihWjEskVOFc6w1ydNHRj+z/DXT8AFXmKwB4WJEKTcjyF+oXAGAogB9hZN4YqnlW7tR9Ak5+IaZGTSV8D+3YLwe6qfSZJHLj123r/x7Um3+vnjOWzZwRwrSJVRDqIC7pskXDb9TOvu09KhehfBX+B0b5trvvBBIC/tBkhfgWHzTHgqqv2uC6AZ5cMOk3YmMPGiQvs4Zz60aZNmnUt91MTT2qbUDEAumhEqTeQBx1jR+S46EgPEQ/oczAs4t7CukJoVvwIA2BXAhTGb/J93ICszf41dkwYYQETWM6QhRYmTwC8GF+8SsYZeOGQyBFalCbvTiWv9sqcNoqREiYjOWk+Yy6AgbEY6+2eI4w5R0CBX4s2hCmxIZK2MRLGm7APtksCtd0tOLQ8c2wYIwYE1sOUAYS2u/8yf497eNdnEZ7WHs9jXgBs5oJwlXCalAY5VNg6LDfWxerHCLli69YNyC4jw1m/1ZfsFsDAkTQGfGfV6FBfWHpzWu1akbRV2Vz6VwkiYWNOhLIznAfOhVW2wE6waXUMMY+9cL4jmEOFmY1z9zK2MWbmKYcVIdD0+vO0Yd5ztFE74CHgU82+RR2EXkAempEADzjggLJtiE6cfFgCFcKlYChFk0NNIcpSSMCgixDv5G/z/wn4Zo0BY8bYwbhE7qf6ZZESYDLVJ7Pz5Y8CLjxw5SBcO197SoBXSdlidABmCzEkKwMugMMsAzjm7z03NgQ4woaIXtBlco2sGuXgkhOdJo8PIMT42cpLmBfrR/9FSBNoioNjDAzGAZRtd8S5fuuIa3kH5tzHWBdZ4cwAoVbEypejryWYWxghJI1ZAVbkJVmUYj4FSznmPm36bAAzucjhoj/Ij3M5xDDtnjO6KgswjEM5YJgs83uWXu3ye/pYRIXTyHlUGNuiEIBPKoDxanuvCKE6F+vm0Ob64Tt/RyIBbnL9jHnAycre2KoMG6/iByAZDn+Xz7jdtYFZ8xGrqb3LpAx1DvKgT7VmJCqrkce72arujQ6SBCrJWRKm3QeEzdTw0bEJ9BLQbTdB/J2iMFmNJRNaaRSLBSSFAyaUsbFWB3jxO8nRwm9Cttg+SiJfe0rAvKZ4yMaKScwnMAAAABAYnaYGcgzn15kxYApoY6zk6dncXA0u231JE1BCgsyUHMGIOoQ+1dezyhAjiGHArpAxlgGrwdBhDRkBKzdd0+Gzg64EuDkocsKwbYwYwClVAYADNAFOW67FveUWAqNCr86VtiDkKD8KqxALkwDGOvM4hn5r4xn0PTlJX5CvKkdRmQ2RgEVZmD1nXbf/w9DLg+MAA/MWGMyja7s4h+7mgAM72mEMYpPpZWOWE85pB4Loc+Nd/hpnxd7HGHOLJMwFc0Ak0bg33/SLcQ7kIZD0G/DHHsAXXTxP02vSHVHtQXmZRUO1RkznIE/joGjCBfIoG8zKVg8d7Iv9DikejJ7EVaiecWZYhoC2t3qG/NvqwGh4gpgORpFSkCqgFIb/U+hbOQvGq1AURa0IJSWTZVSmGxgsvVA4EGJRlRwtCpf3aa62YTzHcg3AFzgCkrBoAKBEbwwCgyQsCsgxssAd5sxKb5umy+3i7GIDGThg0OEzByaO+Ft8T+/6HSaEgVTfi6PNgDDkgBywyDhiSADSehhZHzKCY+mDrp6DnIJ54kiKFkQJpmUM9PRZ1823dJxyKkAS9gybJ4Q76Qj3bdvcXzswcRxwQJozA0sI6WLjMKYxB+rvxj+CieOCoeYgCaVbXFIP/fb9TLPu51mBTfPRPBWmli+5jJPQOcjj7VNsDK3tzCynJ9xZDxnfA3HQNU+IkmOkhXCtipQ8z7CsevBFW/N9dYBuUvbGRCywMKkBD06CcBPFMM/+jJwI3qFyEFiVoMuXmWjdqOXVX5VMGDHzUaiPgcNM+Sz3bFMZvVlgAmCKg2wcAMJ2Bx0q/AocYtQYOnrQCtfJg9yBRyASI+B3fr/dPaI93qONs54jv//odcCXrPQHwIyUCIBHFwFO66Q3zGU6EsuFAebgDoHdIksHXKA9QF/9CAAIvNkaz0IKkT9YAyNYP9fvHa7lmpM2ZJX/1y5zC2vJcdb+ZQmGzkGeZFM5KsI5cvLQo4zoPIL0wIwHz4JXK2HeCl05LsCfDp0Wcpvn2nnOcIBZG31hsprMlJJ8KHklSqTIi7GARw6RRNt5JrYxJZkcWEHtS6pf1ptaPRzrtgUYPQwoNor3zNhhpIQoMVcMYQKD64HBorII8OW9DsomP9fPW/Re+butdC8vzAAAIABJREFU+4uMgWdgGwMb7KowOT2zTB5Vt7N166tLr6LzpAsofSavrQ0d3eU16iCQ7EPPDw3EbScD2Ij9Ul1EH9irdtlX5yBPwqlQBIBmZwtJqYzxdg9b/7tBxisVV8euyNMTjhBrl//j7+vWmfXny8/LAU59D5hRuBSs8BRnwFiRzyQfyuSZd4wYnxwTYEXBWzl911xzzdIe1bKTdei/x1goryIfRogEq6dwsI3GsUmMYgKHrYFDymd95IMZxZoKe3MGOYVyUunzdQnRTtMp2k5Xyh3lLMtrBprSTi1np7aTHxkjrkQrRZI4zW0Uzu4c5Inxi4MricLwUvQYuu0euP53D8/wEoDlzuLvaukxwDt27ChsgdBu0+vW75Gfux3AXciXIjI2JAvLa5LMDtgZZ8YIwCcvjxPQREmh9oESaQI/8RM/UcIwkqeXpc2nKdSxfcdA8D6FuOU1Wjyl5IYEaI4aw5hAZn2ATPbV3n3FhtErVs0qcRFpHcrN2N+YYV6nEO2kDtL2SLMSNbOQJNOjurWPbJmQMycBsOY8tBU96hzkqe9ipaxtXeQqiPfPy6hMAgOGGiMjIdTgO+iggwo7iLnBtph8GJ0Ee90OyMl+6fv/Ae70dRSxtKeg1bN2TYmyOxTTImPBb5T5kdRrsZByCL5bZ+98UpF3+f8wEsA3lkOqhoVTvFPKC4AWXkwAsTeASJkMVybsCydFXqS0Iyug2SCJ/xatSE0ak4646qqrCisvDG0hAKKlibPct11Y1/uxZ4gFESe4xroF9qatV+cgz/JfFeAtnLDCi+JfFOTpRIPMYBOmlZgo9wfbgikUx5YDFMn1y9xnXQfMJrTbBLBC27J6iyuACGNAyERIH4vEGTBWFhkDfid/z2bzxq36TJJ426DO25q4Q78OoEdewrd/+Id/WAyh/EhlDJQ6sHgggd5wAU2Czb37RjqIdCNVHqRy2PGFzRFhAvCMecdYXgArZpKjZnUqvcqx3gQb0+czBqmgbJHIpLzyNm1N5yAPBYl+ZCwtnhBWXcTwTgod0IsaaJZ7C93yqjA6Sq8wIsHktHG/yfvn//tlC/WhyWD86NsLL7ywhAHVspPvqeaYUL6VVcbGMn0O5Cm0KdzLeRC2peAW3TtwLEp/kecQ4sbmc8owooyjlc7Pe97zqne9613l+wzh7g0oEmQNQybB3kk1sAjBqlMlOuScWmQkFURoc0zgrj7P6TwOLzCrZqgwNT28jH5N23m97SRHdYOxdxa6yAW3jWab46lzkCfsZXsfZSystmM82xwgJpmtSYSElWmxKIPRt6LSKhVe1rJGPwfl9YNyVbLgQepLi3jUD9LH2DuFXM8666yyws3YaqN9xqcxoxAs9kl9PSudhrwtUV0xD/EzsAc8y1sS5tJv3tXUU+4Dq8egJrgZBrjJfvhoGY/YO2E05VEQCHJM5ZpaUdvGyschztV6m4ANQI+NtaXd+eefXyJl5nIbunaTr8HOwC90ogjH6173uuqKK65oPfe7c5Anf0EhTyDPNj+YvTY71mBjkIFJeRLQsNpoku+tdhLOE8LF+iXYWz1Ya9L3AbaESvWhlbLyQzC2ttISQhD6AxCaLq7Yrh3GldxPIWD3MgGtFM/XYhJgLIQgGEYAwsp4fWkFrnC4kkiKyWL1Euwl0FslyDT+gDvj0ZZzIlD0APZOrU3MlgWFY8q/22pWc9CAD2kXimljMKXLJNBbzp5KKVLsWOFzJXhgIzqyTRZPv3YO8iSkYtgkxUOsHmw7A7vo310bnczrshjDPS34ECLynUkr3CfJ0QBtk1FctM35uz0nij7RN/qIItFnAIH+1JcWVqj67zuFXiP3rgs5YpiEFoFK1evVj8rX8hJgNIRvJRnf9KY3LQ7gkUceeV1dPX9jZBPsJdjrE+wZb5wMesWuCPYWPvzwwwthgGlR71HqwaaAu/pMt9KTbMxZMrEQo0vd24U+H8o12Tj2zXgSlbJCm77rikToHOSpmWWJOQNtZV2XiZshPPVl3EseAQ9MWA/gY7B5IfIrhPbkFgyl47MdP9pvVp8EuMP8WqyDBXboSzkxKvyrBG6idAnUKXv5pPLyLOjQtra9rLoi3ZTPZIglxeTJ1ZXOocyK1ffynVTaZ2SBvVyckUCvD6AH4JnvmBWEgBJM8n3ZDfVdrbQXCeqCaVmHeQ+AcLiFbE866aTiaNukgK3tUgeP0S6yW6pC2FpQOpBaohaLdpXz3TnIE4bBhFgYoXSCB+y64wLsodWF84RweR+A5h3ucIcS/7bBN6aGcCPUl4N1T1at635yfTLH3FEWElCBc3UVeYzy7oTd9R0lK2RqclC2fYQKLOIQIjZ2efLG0yZ68W0aIQBPqEs9KHLVt5KOrZTGzip/A8wrS6E+l0LK5mmUXUl2L0FfW6DPWBL5sajKIiAL9iziU+4HkJHrK5RmnHJI1MVb110slp3D5izHTD6iiBy9aI5ajKJiRkbG5rOdSC5jzvoE+1IbX+q7Wky4lkyesAzmzGII+XEmVR8gL8AJAAEQuK9irAy1/Cp76Np83oS2gtK+gwZq18xQtCvffzQh9I9BD9zxoO13itHRN8aMJGf5ML//+79fGJ2+cyo5AIAHb0teqXBFm0vbl1W86/h7IFmfW2nL6XroQx9ati3E2AlZSO/ApJibFmfYOxiLahEMRagPEugl0FsW6BlvmOJ3vvOdZWeHU045pdgo4M5OD3KAORby0I477rhCVBizasdtIpsvTG0ho90YgGLyt0KevqafpUH14Xivs+0kHzqMPsOI0mkcB+sGbLtJxl28OmPyTARxfKtx5N0Iu1kd2XeIFJBwT+VUDE5lNh71qEeV2mrCcELJBqoQETbB4MUq+Y3frvOgGmLbyRSYphQoUbkdvBqhdCyrPmHcJeNffPHF1Uc+8pESWl8FAJcIS4EBmw4rzMZcLqELBTN5TfIzx3ix0ijUhiJXwM0RxtcOJhg+zMHxxx9fkt6f+MQnltW4ygww0An4EuzNC/ZibMmD4tSL8GCj6H6hWTaBQycEabFg5IRKDTFGhW2trsXCbCKbZ8cftlMZFbKUj8eeqxlIdqIvFj+uQk8P0c7V28TmsSXGEkCnFh7mGIlgrLF/bB0Zd/HqDORh8TRa8uq+++5bkKsif32DvGnCNlEJVUgQSyMvCLiQD4Si590xIPL2DNqkouejouuyjs8GuIMMMThCnga2MD4DblGOkCxWJ5i7Sy65pChTE8Nv41p9vwvj87AsCtA+3n1bW810MZnX4ZrCPlhbe09jbBkJYJ/hqBts/2doFZ8VppdfK2QmIgAgXnDBBWUrO2DPfAYOJ69Rv15+3jxAaDwEQwzcCfvbGUkOlLEkVQBAecUrXlHGpHMmx4k8PY4eB1T6iM/2sd60F90r0qJUGXBCn7PlbLoySMGAisr0lU7Ttz1oer+we0gjBJKUI4ss5BuzbeQHGO/cubOQYa7fxaszkCcs4yHsdrHPPvuU2HPE7psKq83zDU7AjeDld73xjW8syfUmPG8NuxB19gBBiiEH7mIgzyA3BoBlyhZIsrUVZsbewxKaJTerQ2ec8G6US9E3Aa7b7Pum16KshA+xjNrKQHBcNjFc05bysQOOFA6AXr+bfxyqSePq/4y0vwGBGF0MHlCoOHX83rgRUjNPGelZ15p2/fxuvMDP2AH+RW+ExOgdof9Y3CNkhrXz9xg305wE44lRlivKPnA2RCE26UXfASXC1eYfFo9uD/0uSiY3j55Un9Z8pcOb6tuxnc/2WSCotqti/RZaCNfGqmTyYxuxoGRrwSFyrO1XZyBP7pIHlFMF5NmCzGAAsobSmcEuqaGnIzBLynNgGKzmxO6h6OVoCCtalQvwGfDhreiooTzPKttBDgGgDWKKELDD2kiyl1warB1lKUxOKaCqgT/eYch0lc9RvzegCVzInwDyGArfJchbXA2ZO0IWt73tbYviA9yMk3kAl/MYZOyehVMWVGFkjCt9xABhXhWq1W+MDSM9zXjPc788Z31AoLGB+cW8Afx0CicdKFNCCwMs705ajr/NG+43duh99kvEQW6usFsXxnjxWdXtL+k7+pkOp8snbbj/0/nmsgLnAI0FU1g+0ZtNs5HAHZBL99BJ7Jzxw+kgj7qNITupAxg+f0eOtW1fOgN58hawMhKrgTwLHDz40Dq8Dk6AUrlAVvVJ/MYWAHsHHHBAWbDhO8mmElCFHIUePZNOHdpz1QdS158NVKFNwM7A5jnzTigFIXChTjLE2gHRchImS9m4xtBkqE3yTjyHkL53fb5JCr5N80F5Yc+xIsYCFg4YawKmGF0G3Thj0I0181VhbGOLQccmKC4qsRngAwz9JsHe+oC2ecaE/nQAd8p7KNclj9PiAKwdBwDrK48MY4xFcW7TseA3iiLLFbbSloMh7aBtY9zmXGvzWvSdSgPypAGSafaE7uYAm99StMxxwIbM2Yah6fZpz9DGd2wGIoiziTQCeEWAfDfLxmGU2UTOaxc5352BPDVfKGILLm5yk5tU8qyGjup1AjYJbSoZXP6F5FxsHpqfYcLyUR6YA4PZOTw7z8rbCdA3q0PbGEiruIZJ6vBcJrPn9LyUrG1/KFFeMkXA27WKWemc29/+9iUsp96cnA4eHiUbOQlDnvzaBvhjGwFVTIC2J8hrbkIYRDrBXJHjeMghhxRwBoDNY9CnnWPsBdgD5uTuccKMQcZdfyk2ythYXY/BYXSAQ4bb76ddN78bJhjUX+afMcM5MJboHYv7MHZyNelqupne5khyApyLJVm0v92T8y8qxennnAizbcpKe/oOK855or9n2R/6km3A4AGDT3jCEwrQAZBFyyLMO+v36/p9PDdbYVGP8SjKcPbZZxd20/eIoFnPZxzLE5WuREe27Tx0BvLs82lyybux8AKyXTfGS3uxkRA2I2F1n+cB9ITvhB2BPzlmUDu2Uv4GJWRQC09HCDJA35BBTQxCbYxDu8khmDqJoowkg4mtU+eHYlVbKvLs7Epx6KGHFuoey8LDpiQM9nV4/pCDd89u0grdC/lgDLJWXnOQx1BIWOfVWuyEceMgMb5tgirXM1/l6ek3gM/8xChbSQkMYHvMU/rJuKyzO4sCgTafIa/1o3zMAHWAvH4VYgXmjSEG1MK5Y489tjC4oizhdKvnRke11ZeuI3JDl9H5xpNcvk3YyxrgoO88ry3NzJu6fpz1GQngN5wu4UpREDaDcw8IrpsdmPacnoF9RF6J+Fh9TEacAakC5jH7Me239e+MLeFaixHpyLZJhM5AnlWIlC1jbzGDiUcg9Ycb+medqJMANQBFR2L4dKBBS8EI6WKs5Gtg+uybSwnoNDs2oGLliDAkkc9nkLvuEICfZ4zBqk0Og1bo1fNSlhSrAphKDPA41I3ynMCu5/b8/s+QYuzkIfB8KWfhTR6cZ163/o/xafLqZ/1LyW1iCYXmsG7PXzAUV155ZXXOOecUNkQ4B8tiXrQJagIYAAWUJ5ZZn2ETMLJ217CyV2hX/hCwIMpggc0ky9cWSGjz+cZ+LTIPdhZICN0jLxqTROeKpNhHFqNmZSwd6zznd5GHqU3GqXHC0cNCc1C6Knmx58xZ7f+APIylIvWANJseenGrd7qe3RTtMbeQASI8QueugQBhE7a6xpD/5vkQH8LTxgX2GNlh+0t6B16YF8yys/SQYtxs8dqAPNWbATsrVRlHlKQHGHLHzdM2zwAEoesZEh2MHZADYrN1wAeoVczXu2cHfiyf5gmisckF8AOg5DqYCK7H+zFwXN9hkgQgDFBocM1zBGDze4druabrOwAv9wTCDDLPwsjpJ8ybUIcVP0IgclGwdPFc8tM8p+cFaAFeCbkSlIW6Xd/9x9DfxoQcTMCAFx/eVtuU+mpVefd3ZyiMQSEc+ZnCqACYUFjXwKUOHIxx41tqgbFtdw1svP7F+inNIiTFEGFtsX3mqfnB0AMgrufout1jvD656XNyJE9yJV9yJm9jQtiKgyxyooad/qFr7LBAJwnRcrajfE4ffREhW+wh3Qdg0nNj1wOeD2Fz6aWXlrxXAGYeOxnnsAHsD7tgBa40Cg6WRWz6HpkQJIBzh2oztItNo8PYTZE6egJrx+mwmIyTEela8fzzvAOE9A4mmj1uO1LUGZMnMdWKVCCH52PyDrUD5+mI+jmeA9CKTjfZhTHR0UK2FIAFJ8Cd0BRwAPQxbt4pCXlJ2Axh3uc85znld69+9atLmEmdPqtSxfdNKsoQGJTrYBCYMCaHg0fk8Nn3ytRgDAE3iolna/AxWtg1Bk4oiycq3KpGj/ZSXhSqVa+x2ER7ATsATx/yonlzloL7LYbEfQzsOiAln7H0tX5X44iXBtyajLt27Wrd2+oeZq32DthPht2YF85Xj9K47APkAUvTwIW5QS8BDfL21EzDUlPa3nnnQMWFF15YVt8zdBgNgMSc1HbX7QNkrCvgC/mE/Bl2/c6ZpOfInnzJ2eIZTqOUGLpG6Av7GnnPk2A75N+XbLTbuLUyXPvct23WZbWzdO+7e77du3cX51YURz/WbeE8n9mCsJVsmP5kR4LZw8SaTwGQhmQ7tIWtZ9/YePOfA0I3YJONW98BfsCsc5u2H8hl+9lV86PtXM/OQJ4tOrBcQnkmLS+t6cPPM4CGck4MBB0GaDEE8hCFE5797GeX1TOA3zHHHFNC2IprAntyvYAocsJ6ym3j6chjcL6t2LAfwr8qr6vvRNFQfq6rOCWQiO71nb/zKgA3K3YwiJQl44ptxFi4h/u7Z9xbW6wcA/Luec97lvtTulaq8bqEqIXXGEZg0nMa+IsM6qH02bztwFCa1PIwJXR77rEr973V/XLfSCjG0MjFsyhHSJ/RXjVAAhQYGG3B8nHUKFxMH4be/LNCLuaieWi+aT/22gpezyVc6PecMtcyTzYBCAZ4A+AZKPnIGDZzRrSCg4TxwIArmivlg57i3ALV5BqypbOEZeU/A9RsRgC7vgHdNOCoLSIc9KMxjJmSlzdmNo+e49QC4qeffnqJOs2rNyfPC8DEdhg3Uij0Od0aubL63ThCXDgvgNPktbr6vzYCpIgbDJtxoDSMPFBMm3QkiyosIjS2kS5hBxdtkwibOcJeczrXBuTZ40+CMxBhhS3QM2aQt1UHGzDoXZ4gIyJkyxsA0nhHjAgWTUgC0AK+rObEqEWI1H67+++/f7XffvuVhSzK0vg8+d0Nb3jD6sd//MfLYTu5CBtjEyN/zopX9wI4gT9hKuCQAmbgDDhGy2QDWA36rZ5v7H/jwQkdkaVJTgG1TakvB6GG/2shHwZSbqMQKaUJBE0zpkP5zvgHVLDfnBxlWThagJ+Vuxwx3rwFHfLFGCqMoLltpS+mCoMeYUXX88wAkSOAC4MXxxCePdoS79oZh3Z7BofnAXyETrH6IgTKi5AThoPREiEQZiUnbDhdx0jW9U09b3kIzz+rDZ4ZoKcz6VNgH8s1ZoePnuPISzVirwCftvQ9PCACZewATeaQeUXHcrLe/OY3l3EWdWnZoSAVlsUSfh+HawbT6F7GujFpD21jWB4v5pFzgnk2BwCztuQAyLK3Qr/GV9s5350xeVdccUWZ7EIzJgUPb9mOaUuofV/HcxtIOtPg4KEAClbuGjC8f8aExxAhDF6vQSZRnUIMZo6C5PkYdHKKJI97jwMTd+Mb37iEhp1nYJowkjp5yIo+G0juJRwcoSdhV4DOIAdKeScxqfqW19Dup6+wpwA3ww6wt+1tDR+mLdfCa6+9thgJ6RvCNFI5gIhZBnUI32sfhc+4Y+aANeySRHKMAyYHmMNyAHdAHkUNyBgnDkbLXOVIAYjOwwKai0CR6whdmovAkutzBjFh9IJ7AlL0pzYAVpNgMQBjALF4930cAcr81nVcz3Vd333oAffERmoDfYRVCJ2EscRcajudJFogwiBKAOTa1gqQ87wiAJg6eovxDsaT88igxyIJ959kPIfQ77PaQK76ySICDjidK8Q4Zl0A5LEHAJ6+ZB/a1M/sIpsI7BkL2DHRL/aObQOwAC0gE8Aif7ZKHrvfAJ36IGwWG8tuxeH/dbur/fS5aJS0Jn1tPJrHIlbGbbDLHHvpOQCfOSnUzHa7dptYxvU8O9su+tl2DcbOQN7ll19e6E0gz6SnZNoUTJsDbSjXCjAIYBlM9QGJFjYoDTQgA7s0eVDowrPYPWwgwAi4mQgB3gz48IaG8txDbwclguXESgvVmJCbUD5hOVh3/a+Fszh9WGv6AOgR+p9lTNfpe0AQcAoAiLmTT2vuUdgcNawWQMRoAbjGkMVMDqs1pbPIRQMOsRhCwgASQKgMDGaQ04f9ZOgsBJIKAiACTe4HeNYP31ngxaEDrrAiHDy/dx2Mm+syYspccAblBFkQwznEvmH6tRXzqp3aK5dYWxlC51otibkDWt1H3i+jCSQCjcAkvTR0QD/PmPMM+hnYkVoj9QUokYow1hcAK98MqOfM0IVd6mu2yT0QIJwPUS8ONqLIOLS7jTnEmZKiZAw7x1ww9zgrxlw4Zv7PWTEXOGXGqfEq9IxlNsZd1zg3/8xV85azw75Grl3Xz8y+m/f0BezUZgpAZyCPUAhSiJAyMEES5M23Byw5BeAz6B3hmcx6BwwNFMYEyMOYUECRLxDXzD6Yrw/qk5qXKIxtEY1wI3ZjEzcpX9SQCWfxnoE7Oai8ZSBkHsO6DufQbQ5MD0AzyZpxChieOBgvhodhwpABcMActgTQCoYMKwZQMUQWcQFYjBFDF6DLntsOebb1QzqGskb0r1QPcnee3wKVAIrrMpgAHVaK4QyACfgpByFMDVQCk4BbsIrxLJ7NMY1hJA9yWYc+nLeN+heosDgH0AMYpCKM9QXkYb2MCzoQ+VDXjV18ZqPYObaL7nW4L8LCIgftwCabJ+aIPF9zI+ZFzAdzIHLPfdZn5hNwh3UH1jk9GHTPGIxgsILa0Bch4lk5Wg7P2mYKQGcgj3DQrHLLCBTF2sWAyGv+CLSQN5AnLATkUeq8F8xdyqg5sKvLzASUl4XJAPQwIpipfM0nAYYC8BHOk3PKM+d1z2tYx3ZegMI6IASaZoVPgSvGDTCW04udw+RhJtSvZKgsbKgfktqFuIBBebryoo1bDKrruJ7rYiwwbhiPWeFhfTdGwLbouAJ4OSxYaYtHMC9tGuX5ZlU/Z5m7IkiIGg4JAFTXjX1+ZuPYM20QmRKhAs6wfhwNYE3qAzbZPDFHhNY5MdJD9DcbWQ/zChUDc6smP7SBo6e9QtFt5nx3BvJ0hkRKIA+lL8TY54DYtHuZAGQs3APkUUBCRgDKpsmi7ec1AeWCWPUMpCgfQ975mk8CEokxV1FSSO6LvK9Fjeym/C7A4CLvAKOwE8YOyBPuAuwidDrtmpsi12Wfk4OCceFIY5EADGBojC9zV9jSYiNAqc0FB8vq6Xp0avIznQ3M0TXyRumbAHNx7rL3b/P32iZ3VbqVudnmeOoM5AEXQgBAnqXHvIE2hZLX2pOdMkgMDvk0VtWS+9Am5br2GUDHMEikl+toVR1qP1/zSUDOEs9aGMXCILUksUfLGtv8/ew9ZuWOybuTb3SDG9ygrGzF7AN5KbfZcptHNhhPBlkZFQcmdawhWyDPrg5CnBjkIYG8rewJnY3lU2JM/ign3Xdb/WaVf2O/5c0CpFj1NvM8OwN5KFXxckvN5XegSVcpxLHf2yCRFwNYK61C7lbvrZJeH4vMeX5yyig6DKk0BAokX/NJwCIVDoccMbsXAB9AyDwGNc9ZDJAAInLqbCsJ5CnRJLybIG8xedbHofC1FZeYfQXSAYmxbnEG5Hl2i4Y4CesSGQLohD0tYLLLhjDukEGetsn1lgbgXTWCtl6dgTzJg5gPYENuCKM4FqM/xOcQHqfYLTnfd999i/JRWRzjBKQMsc3r1Cbj2fZtQjQ8Qzmmba6AamtCD/E6QJ7k/Vi4YoWbcGLdcObn5cFHXYaYUoWFMU1AnqR0cgdQ6ufl5+Zyl58INEiNidqZqh6M8QXkiRBZeSrXbV1AHtJD9FAxf4sttN13Q7U5QJ68XIuf5M7a57utV2cgD7ggXCDPKpYEeXuGV9sebECexFNJpkCemm6KUVsCniBvedkLU1jRZUWdcY2JajM5tq0JPcTrAHlCEUK1Vie/8pWvTJD30ebgogkgs6BC3pgtuBRHN24529j+JtfJc/fuJ6AHiKYPMHm2OMO+jPEVII9ju05MHkBnQYaoi1W1Fs6xkW3b3bauF8yjVczqBGp/W69OQZ7Br2ikGmOSINsSSF5nb9DCw5JYbQWj3TB4mOQuzJggb295NR1DQJ4dG4S/KA0rFIGXZPO2V0XkJJ9HiQ8hW7Wt5J0kgNgbQLQlE4nmWAwlVIA8Tp8Cs8mgtiNzjChm1O5BALTPY3T6gDz7pktVUfJnXXLygCTRFmwrx9LKYCBvqLZQuxAyHDOLRXxu69ULyLM0OJm85YHGVsAEyONNqnt1k5vcpNTGkiuittBQB/ZWzzO0v5EvNko9JjWXfG67Mnlbk3po17FSTMV4Tp+6VcalROi2AE1eZ2/gojyKOmLAHZDH8bPClo4QbkyZ7S2zeWVCfkJr6rXRBVI4ONTyqMbm9AF5GDFgScrFuuR4A3TAqRw3RewtlAFQh2oLMXmIMLrRwr42c747BXkAh3BtgrxuAR5AZABbwWhJv23NLL5QWFXyqQE0NNC0bu2hNFTyl8AOqFAaV1999WjrY7UJFNUQk9No2x5FupVjwOwJHVoIkDXYFgccs4CJMh92GjrggAMKwOP4qfMoTzdDts3lLUTrMF6x0ACPcSwcbks3hecBorGBPA6aaBAW2I4Xkf4zVLAUdoW+1l8WfyoGDoSrrTfEdmsTEoF9UXZOxGgtwrWUutAhkKcqeDJ53QI9IM+KL6HEG93oRkWxM6q8sAR5y8ue0gBGKHQrbDkuCiKPtQhqmyCP4VNiQuHe4447roRAQJeyAAAgAElEQVRslfqxn7LCsvLHMCMMKMU8C7jk9/OBEzKUTiBZ3lgF7oQUpc5YbZg1CueTo/FGlg618IxTW7edeeaZRc+Sq/2I/f0b3/jG6AAeHUC/KfZsuy2L+tgYtpw+DEA1xHfto0/kElrwpc/U+wOehtZe6xfk08sftF+udmYJla8ub7SH1tHLtgeNrkyFbY8UPwX0bByuxlGCvOXHC+WgDJA6RkJgcif02RjzcNoEeHEtcmIIsUgWAADLcvQ4JXZpkacn50fRZMbUwhaGNXdbmB+QBAjmjGBKVTdQvFvY1lZyQJ6dL2zGnoB6T7kCauRGLsacsadaAUBsT2BbmdmNwHhV7xHjYsXmVVddVQrXjo3Bi3nrubB5IkIiQxadcXDJCcOHgRoicNIuugabjc2zalVfDgGcYu7IjM2WTmUXGkWQHZxdAK/N8dRZuJaQeeuK8tr0F6O0LJDJ388GKwaMpdcMp5IJDnWcKKshDOx17ztA2TY6PK0DDzywlFPBVrdZmTwU6xjfKS2sAHlRYrt27SoKzb6tPFisv1A4hcyYvuhFLypFZilA+XuUX4R1GeQANPm+N1gBUiSam//qEmJhrC4kY8W8yTd2v9hU+RlDcRhXAIG8UYDOdlivec1rqnPPPbcYXmlH0mDkd6kUYWWtunjCs5yXNg3yEOd+AD1zlmxs5YZAMK7MzUgJGlIoFP4A0mEQDrl3LCydvSpbRD7siKibRSGiGParVoNQHp4dq7oI+XcG8jwM7xHIU19MEuSQBsGqOrqr+wJ5PHQriQA8ydbCCXJz/K2r+27KdQPkof2VTZCITLmZlPlqLgGAj+wkq1922WUFwFHCDAfGQL4T1pQHfvrppxeDqySQ/Vlt1wekMMoYPwBwExk/IAWjAqBYNUsewrS2M5NDxeETYsM4hROI6bcLxs6dO0sOELmNBTTXQZvnIhdOLtkYJ3LpsMTGDgOrOLQ9fpWswE4BA2wWEAMUYFYQFHKkLFjh5GGj22Zams+e/n8RTprFZvSeRSdkhYXHzJu75E1GQMwq2L0AUcKfQJR+1ZdKv1hp/tznPrfUzqPLu7Rb2uFArph3cgExduRjLpKdsSad6owzzijA2XldVWvoDOSJ49vOTE4IZe0BE+TNZuKWHXQ8FEnVapEBeD/2Yz9Wcp8oMsmyy15/039PafG0hL6iACp2us3cif5V97DuyJAAfl/72tdKmgHAQiHydoE9leuFGyP8QkFiVpwjVwirwKDTNYy8AwiqM4ABBIYKbOrti8/a7/As8VyeEXABWKz0tp+yfDvg5JhjjikrmeWLkSHWCYNqDqtRiOGzKvSss84qBjDC4q4fR9xz1nu0ra33WfeJ5452TcqAHOIA9rFsZGIRGrkAcZwDeeFnn312pQ4ZB02+onD2iSeeWD77jgMnT9Tv5EgxzMKxmXe7t54wT60GtQDFOMPsAcWcNItQAMEI5QJVAXzasiNxPe+uH4CKjmbztElKiNI2CgvLB9ZGaQyAqPPpdIffx1G/7qzPca53v3cth+d1AGxC2cYlZ0IbQocZdxxYZVIAPoC4axvSGcgzOXhAli9TKjwoQmurk/M6ewJG3ovQl7pNmDwgz8ovCo6ySnntKa8m8jCZAWWT9YgjjigrRHn+GKjMydvbACzzDaBHpoyIxRq7d+8ueoNBEQ2gR+SeMsZPf/rTi8KkzBls4A/IETngYAr5cnyEmDAxQKC8HIwXVidYwAA5AMU00LJMSHPa9QK4BNsEnACnwktAivZppzIowTrZohBAC8ZJ2oDaZYCvZ2fAhL2BXoAXGGJAMC9ASoTc6GAhcCyC/DLF0zGlVh8CitgPK8eFK+WhSQFhIMkQg8poMeLAI5kKb9r9QTsdIgdbHXGelYR+6xquh22RkymsDGS5r/vrP9vgWdmpzz2fbTIZTaDs13/916vTTjutADfhVGVijAPPBcCRDzk5x3gRgqUnAQH5n/oe6xOLCQBi7DJWBTBOgDd9Nsd4uuaaawqoMZcuvvjiks5C5oCMciD60di2+4Q5zE4Zl3TqJIiq6+TJv/k/QOW3rgFEyZEG6swT4xWIRygBUua/75FN9InfGzfGhjkk6oV9NO6MV/MOKDPX5bFb/OBwfYfPvjefzdfI1TQnpEaYmwCu+5qb9JCx6AB+yUIUwu8AYO365je/2Uu4vzOQZ6JQJlZ1yQOhJHSOjiLweofm58UBSMgOJUxJA3bKJiiZoBCqgW+Qxnn53kzWxqpxSxmo82a1OINKKWxi2Ga6yu/vW0aXARY2oyh50JQmg421EYY89dRTC/CxlZckeWkLAA0wJBFbThplDNgw+DaYB4yADkAQkAS09LEDIFz0iGu4nusGcOPF04nuDVQBMLYhw8YxEtoJqMgF41jUn4OhEirDBjAw7sGAmtvK+mw1LhlnxgXbgNUA8E444YRS/1EYl6zcK+43+X9tIVfn+hz/P+qoo4qM733ve1eOo48+eo/Dd/rA4VzX8FvXicP/J+8X7fA3oWaEgfYKQ1v8QA7Am35/yUteUow9oKgfGWxgADAwj40XIA4wMYbSQWtv3pqX5ErOwJK+ALr1mdqiPss7A9o5BQAT8sG41UezDn8HwAE6zhGnAEATItb3mH3jx5jC9nMIXFv+IEfRePcC2EUIzDM5ljHOvDtcw5h0uJbxa6yZf96NX89RH/v1azjfvKR7OCDawRECbukobGKAuvakPt+VOgN5BAz1UqwKcT7sYQ8rSoVC9tAJNpqBje3khYK2ITmQJy8PuAZIKEKMQQLr5vLmbQbAY1SEaSkDIQpKJBTIfFMtz2pLAuTOqDDSsZCD0cb8xUGhMuiMB4YMoME0MA6AjXlBKVstKLwZSpyCp9QBegsVsBJAvVIMWAI5PozJtMM1efB0nfHid34PlFhUwmDU7+OzezM62Ei/YyQwVNrJUGCcMA1YTKEgzKZni+f03EAdfRvM03bjkuxCbq7jepxy1zau6RrAiOwYKUwXXY71AnaFMrWJsWbIAFYMnxApNo6sgeY4sB0O33P8nes3fusaADqGAxtEVzHS7uv+nhljri+xktpaf/6QQ7yTRxwhl5CN8eLw/NvJqK2xuknXqY8rfaCfjCN9DPRhmuEBgAj4Mx+MewDQ3MF4SYfxLnxuvmHCzNFwDALk+7scO2wvpjCYMeNAf+vneh/77LtoF2eIfgcgzS3X4IBx9IJVNmaNYe/Gte89i7FqLkjX4SwBcOZPjMF4dy9j0FyL9tTb1NfY6AzkeSiCh5yt8LJ8H/LlfRIUZG4CJ/hoDj6mAT6DVd7JbW5zm+JxMBgqsZsg5I1Bnfa7/G5v+RuTHBGTWOjI6ie5pcCz8UyWJm6+hi2BUOyUfih3QAELKJ2EZ88IcTyFNylvTAEwot8ZEPl+2L4IF15wwQUlZAiE0WUOn809zKAQsXIwwp5COMJI2DrXYyyEJoEawBPT5N7yaQEZxoLx0T7tDMMRhqJrcEJecbgXHe4w1h3kGIc2xUG2ixzxe+9x3bhX3DueeRXGcdijez1apx/1r7FsbNOtnAZOAiY7Fr6YN0LxMZfMM6lG5p9UBQ4EJpxOBs7MX8xhgLqm48P5McZjbMd43Gosx1j1G88W43PIvdEZyPPQBCmXiUfKk8WEqDHGu6U0xbYpuAR6ewONpuALaBaysKOAgrMmDHB9yCGHlFwAHkfKeT45M/yYC+Fv3qbVtAHwyNHEztd4JEBPrfIYjyTzSVIC20tg2bm2/R3yjLoEOgV5bsRDEwLgJVuODnRgRe50pzsVOlYIBUUv3BjJmE0BTp7/1epTn/pUyQUA8oBo4RChICVssA1yG8g3ZTUd6JENACd/kYcptHDooYcW+Qmn8Sixezw5SipfKYGUQEogJZASGLoEOgd5IQD0JkMqFCIGbzEGVs8+oFY/SSAWG7eAgDFNwDcdjMwCaShwCchCtOSJiQJULMKQ4yCHIHMhr5cpVtMh9ArcyQES1uaISK7F3pGlsLccIluYoefzlRJICaQEUgIpgXWRQG8gD/vBSIqhAxtyVayMAfZsIIxxkqxsmbHVOcBeAr3rQckscBffyymyKo88FaiUo2clkxI2EryVnVhlte9o5xDeA9wZY5K85XuoqyQkK6VA/qgFFkLe5CifxNhNBm9d1Fq2MyWQEkgJpARIoDeQVxc3g2nljSRKycpWsVkNij2xcMBKNsnOmBUMlbw+izQS9O0J+gKsWIVmFZ68RyBPPSB/A5atZPKdOj3k7fshAK0+2uBZHcaN8WOlrGX70gOs7JMYj+WUu2glMkBsmbzdAiQGY+/WIbG2Prfyc0ogJZASSAmkBEICKwF5bo4VYUDlOAEfVqMJ4x588MHV/vvvX9g9AEXdKKvTLNIAZrCAmwRUZoEhMgBc5OKRj6XmGFGsnWXgQDRZ2T5Fnh5ZAjabsqI5gB320qIUpR+wmVZtKVOBqZMuYKwBwVhl9Y04FhGaTeYu1ES+pwRSAimBlMA6SmBlIC+ExZBanGF5tdAZwIJJUfxSTpRFGgpiAoDnnHNOYawwVAw3A74pxZXrjBSwK+cutm9Rc4icABeFVZ2LLVWGAbDD8GFJAWYFJdcZKHu2+hFgTuhVaBXoJRtMnGrrmGJV8bHDWDpMMVmpJ6gwq4KaGD3L840l6QTJ3sXszPeUQEogJZASWGcJrBzkTQqPkZUIr5aUsKMVosJoWCo7OAB8DLYVoxLiLdawchTgA14ipAsIzGLBhv59gBjPAnhg34AYNbXU17K9lry7YKMAOPXw5DOSQZT4APQ8q6KRZCgkrmCyLVqUCXH9ySPuPe29TblNu77vJtvj+UMGxgU5ALnCrhZL6H8AzRY1Sp5YfMIhAGytjsXSWXwi1w64s2m7QrbSARR1lQqA9QyZTY7H/H9KICWQEkgJpATWVQKDA3mYPeAE2BM2A+CE2ew9iN3DxAA1FmrYp1V5CxXi7UJgex85fH4DGAEMASbaBChdXCvaqc2AGvCBlZI/JvyqMCRwAqQALmTgXYFpDCeGDhtqFXO8QpZC3aqHW1BgNbP8PHtHWqwBJJGZkDkQiQ0DotxfDhtgBRBqE7A1CcKa/t81XEv/uDZw7l514KaMCVbXM1kVrF/JAHMJnKkHaJGJHQWshBXiF5IG4jyjA6j1rJwC53lm1cs9pzaTlTFGXhmWjRGT7ymBlEBKICUwJgkMDuRNCpcBVoGaUVYhXjV5+WfAjnAusCO3SuI8g27jbbsS2D7HfpGADMMORARoATACsAS4ivc2AFxcq/4OWEwDOJgprBR2DaADaFTFVz/wjDPOKFsi3e52t7vuOYFboEbBY0yn0KQK+ULes16YKrlmtpQhJ4d6hbZbwnphBW31JCfNilIyFsJU8V+lfuDIli52AwAOhULtDWkbGGyYGojTDn9zONdvbE6uHZ5PKR3gXXheiNk9bR4upGyDedtDaa8Qq5qKQJt2A3DR59HvxgGW8rDDDis5icqeAHXaDizaeUXoWv5nMnazRkl+nxJICaQEUgJjk8DgQR6BA3qMM9aFobalCXYKEAEIgAGgBQiQSH/Tm960AD9AUGgX0yeUJ0dLiBfwAP4wV3XgB/wFYxUgEDirg7X65zqL5fwAccFUYcAc2CoMGcbMHnlC0drxpje9qYRehZ5tmo5x0mYgxjM4DjzwwOvyx4AXmzwDSK4JvJEJ2WzFRvk7uQlrkpd7AIvCmMLgZBZH3Nf7fvvtVw6fnastgJX2+T1wBYBizIAsBwDq8BnTKvcNQAtw5hpCp+5Xv37cN9rh3T3dC2MJ6GEt7UBx4oknFnCK3QVML7roorJllFxNfaLkiecFfMkHM7ydjMY2sfN5UgIpgZRASiAlsBYgb7KbABoGnDHHvDHuQnnnn39+ATF2fMDqCe0CCMJ4gAagYJUpMKV0BqYMGyZPDZuEuXIdLCDWChgDjLBrNs8WOsS2uR+w5nt/x1TFxsZvf/vbS+j4kksuKaFF137+859fiuwCWDY4P/nkk0s7lO7QPrmG2uizNmOksGxYyWc961kFzGoPxg/AFWYEXLYCdtNkhhHFHGqjdgnzKv77lKc8pSxAcD8MGmBs83bgGWNoU+jYIJpc5bqpKaf9d77znYtcA9jVgR55+3tsrwZcCrlj5/SDTeA9p/5yT7Kx8hXgBczlElo4AcTpG+BWnwDomFl7j2IxjQPPNg/gnZRL/j8lkBJICaQEUgJjlcBagrxZnYG9waYJYQoJKgaM6QEelBbBKmGGsFeYo3333be8+05O113ucpfCFjkXAFG/DyADChVqtlG98CZG7SEPeUj5HkCpgyE5YkAa0BPhZIzVPvvsU5irYKgwYkAd0OQeO3bsKIBTkWihUUylXLXdu3d3EmIMds/1hTOxjwCgVcty4sgQqFV6RCgWuBJqtVpX+xQQvvTSSwuDBjTaCqx++E6Y16bszsNc2moNGBa2FeoFkj2ne7knthNDCbgLzwNu2pmvlEBKICWQEkgJpASaS2BUIA+zheHC8mG7ABjhVayPUCnAAnSoyYchw+YJ/WGWhHsxT5goIUiMGuAHiGEBMW2Th+/9HZhzPhApRAngAYzAHgYMWAQ0n/rUp5ZVwfLtAB8gR55hhI0vu+yy0mZtB1gjzNi8W+f7BXk5ACn3cmDDyM+hDQ5gKw5tqx9Cxtsd9fN9jmvF9eN+9dBqhlfn68M8KyWQEkgJpARSArMkMCqQN+sh43uABqAQ3sMUWb0LWFnlaXGGhRpCtRYDCBEKFQppnnXWWWXbK/XW1PAT3rQNlkUCQornnXdedeGFF1avfe1rC5tlcQIWDCsmz889du3aVUKtwotAkXYkSxU9k+8pgZRASiAlkBJICbQtgY0CeYTXhLmaZKD8H0Cb9n2wU95nMVTBzCVL1fYwzuulBFICKYGUQEogJTApgY0DeZMCyP+nBFICKYGUQEogJZASGKMEEuSNsVfzmVICKYGUQEogJZAS2HgJJMjb+CGQAkgJpARSAimBlEBKYIwSSJA3xl7NZ0oJpARSAimBlEBKYOMlkCBv44dACiAlkBJICaQEUgIpgTFKIEHeGHs1nyklkBJICaQEUgIpgY2XQIK8jR8CKYCUQEogJZASSAmkBMYogQR5Y+zVfKaUQEogJZASSAmkBDZeAgnyNn4IpABSAimBlEBKICWQEhijBBLkjbFX85lSAimBlEBKICWQEth4CSTI2/ghkAJICaQEUgIpgZRASmCMEkiQN8ZezWdKCaQEUgIpgZRASmDjJZAgb+OHQAogJZASSAmkBFICKYExSiBB3hh7NZ8pJZASSAmkBFICKYGNl0CCvI0fAimAlEBKICWQEkgJpATGKIEEeWPs1XymlEBKICWQEkgJpAQ2XgIJ8jZ+CKQAUgIpgZRASiAlkBIYowQS5I2xV/OZUgIpgZRASiAlkBLYeAkkyNv4IZACSAmkBFICKYGUQEpgjBJIkDfGXs1nSgmkBFICKYGUQEpg4yWQIG/jh0AKICWQEkgJpARSAimBMUogQd4YezWfKSWQEkgJpARSAimBjZdAgryeh8APfvCD6rvf/W61e/fu6ktf+lL13//939X//u//lv/7/oc//OHMFvnbd77znXLutddeW7nWdi+/+cY3vlFdddVV1fe///3tTp/r766j/a7r81ZtnuuCeVJKICWwlwS+9a1vVVdccUWZZ9/73vdynu0lofxiUyXA7lx99dXV1772teqrX/1qOS677LLqyiuvrL75zW9WOV+uHxkJ8q6XRS+fKO5/+Zd/qX7v936vespTnlL9yq/8SvX0pz+9uvjii6tPfepTBQDOAk0GNmD4xje+sfqHf/iHAvi2arTrfPvb367++I//uHrrW99aXXPNNVudPvff/u///q/60z/90+od73hHAXvzgM25L54npgRSAkUC9MSLX/ziMt8ZrpxnOTBSAj+SgPnwR3/0R9Vzn/vc6pnPfGY5nvOc51S//du/Xb397W8vdpK9zFdVJcjraRRQ0Abmhz70oeqRj3xk9eAHP7h63vOeV730pS+tzjnnnOqhD31o9djHPrb6i7/4iwLMpjXLoP2P//iP6txzzy3nYf62egF57vnqV7+6+t3f/d3WQN7Xv/71aufOndXpp59ePKg0Plv1Qv4tJdBMAuGcvepVr6rudre7Vfe4xz2qz372s4WdaHalPDslME4JiCKdeuqp1V3ucpfqyU9+cnXGGWcUsuQJT3hCdd/73rd8Fr1K25Qgr7cZAJBh6h7xiEeU46/+6q8K1YxdQzf7/4Me9KDqfve7XwnfAnQOtLPfCtNi5Zz/n//5n9Xll19+HSUd5zjP4f+OuAb2z29cgwGpn+87v3FuTAjn+H9cL87xO38TQnrWs55VJpdQs3PzlRJICbQjAfPMfH3iE59YMVo/8zM/UxgK8z9fKYGUQFVCtb/8y79cHXnkkdW//uu/Vv/zP/9TffGLX6w+//nPV7/5m79Z3e52t6v+8i//sti6TZdXMnk9jQCeB0YNiPvzP//zAtYCWFHqwriXXnppdeihh5ZQrpy3T3ziE9U73/nO6k/+5E+qX/3VX63OP//8AhTR0R/96EcL6KP4P/3pT5e/MQqYQb975StfWb533Q984AMlZAsg8m7+4A/+oPqbv/mb6qKLLipGBN39j//4j4X1Iw6/kSv4ile8otz3tNNOq37nd36n+sxnPlPumSCvp0GTt9lICZh/GP9f+IVfqN72trdV5h9GT75ROlQbOSTyoSckIB8PyDv66KML4YGIYEe9i4bd8Y53LOFcRMWmvxLk9TQCsHW88h07dhQv3YCcfH3lK1+pjjvuuOoXf/EXC8snj+7+979/dfe7372EbE4++eTqr//6r6uHP/zhZQADjl/4wheqY445pvr5n//56swzzyy/feADH1gG+Xve856SMwfE/dqv/VoxEsDbIYccUgzIwx72sJIXeO9737ty/N3f/V1p0sc//vFyPdc8++yzyzn3ute9qgc84AGVNgJ5vkeTJ5M32Yv5/5TAchIwv7ARj3nMY0r+7rvf/e7q9re/fQF8AGC+UgKbLoEAeT/7sz9byAx2TcTqv/7rv6rzzjuvOuywwwrDN83ObprsEuT11OOo5BNOOKEAMQM0QqP12/tensHhhx9effnLX67e9KY3FQ9eMinFDyhi8ICzN7zhDZXVRMDbSSedVP3zP/9zCa/63ZOe9KRCV2MGXRP4s8Bj165d1b//+79Xt7jFLapnPOMZ5f/BBN75zneuXvKSl5TmYPoYGNfiCfGOXv/615f8h4997GPFc0qQV++5/JwSaE8C//Zv/1Ydf/zx1Qte8ILC+FtBSHdgLuiAfKUENl0C7Bobdetb37rMDQSIA1lxm9vcpuSti1xJL9r0V4K8nkaAnAEs3W/8xm8U4DUL5GH66iBPeFe+ngUUwBYwh+kDuuQf8Fh4LsK7Xs6z8pXn/653vavcy+pd15XHB+T52yWXXFKApnZgBHlEwsFeFncI31rd95GPfKT6sz/7s9JueQ5///d/nyCvSCn/SQm0KwEGyRyXnnHwwQdXF1xwQVlFL7VCYrm5LtUjDVe7cs+rrZ8EgDwLFc2TZz/72YX5/q3f+q2y2pZ9BPje9773ldSj9Xu6dlucIK9dec68mjCnQSm3DkM2LbeGx46VO/HEE0sYFJP3kIc85LpyKXWQ97rXva76p3/6p+pOd7pT5TNw54V5U17lDne4w1SQJ6H7rne9a/XmN7/5urbyeO55z3teB/KARxMGY2gxyKMf/egSqv2pn/qpEtIFFpPJu058+SEl0IoE6AQOF4fslre8ZZmT8vKweFbY3vzmNy8LnrDvCfRaEXleZE0lAOQ97nGPq+5zn/uUKJe5Y06YGwgKKUzsF1u16a8EeT2NAEybMiaYuQ9/+MN7eBgGJ0aNly5fziIH4VlAbBbIw+RZCCHM+qIXvei68igGuVVFs5i8rUCe8JDfK+li1ZIFHti8z33uc4X5Aw6TyetpwORtNk4CHDTzDZOP8X/ve99bffCDHyyH/FrhKfrAOZlQvnHDIx+4JoFpIM+f2VG201wRumXvNv2VIK+nEYCFw7ypj2cVrLCposIYOO/+/6hHPaqAPIsZePTbgTz5OXL4LLSQeGoXDDXszjrrrOq2t71tYyYPyJM7qGafNposrqmNL3vZy6qf/umfLiAP45hMXk8DJ2+zERIIFgKDjrWjKzhcGApHFCAXspVqYV7mKyWwqRIA8uSoHnXUUdftGGWOiEohP0SmTjnllJKutKkyiudOkBeS6PidEo98G2yekCzgZAUtJk5I5thjj63e//73F+VOiW8F8iy8MNDl6FlGDiC+/OUvr5761KcWJuCggw4qJVmcU8/J24rJk5Pnvq6hNpfyLfIB7c6hfbe61a1KKRah5wR5HQ+YvPxGSQADYWEUgCfMxLHyHb3hwNxh1K2sf/zjH1+cwo0SUD5sSqAmAXYNW2eRBULC7lHsls8qQRxxxBElMsbmbvorQV7PIwBDBzjZgsUgpbTlFkge/du//dvr6ucZnBY92NZImRRLwXn0QJpwrmvwXAx2wBDostLWNi8vfOELC5Pne+fYBs22ae6NhbOy1r3ihTHQHgs1GBQsgnCRXDzekra95S1vKecIKau1Z0uZ17zmNYU5ZIzylRJICSwuAXMIiGOsrIo31+svf5fywSk0H+XN5islsKkS4ASp8yp/VTRLLUmHyhJsoDQH5YbSNuWOFyubI0Ccuj6o5ShVAmDFy2fnAGl1hR+hG8DMQMfoWU3rPAcgZzskTNwnP/nJ8lvnYehc06B3Tt3D8T2aO2pw+b/fKOUAVPpt3Nf3ruE9Pkeb8z0lkBJYTAIx383NrfLtzHtgL+t/LSbn/NU4JGC+sEtIjvrhuwR2e/ZxMnl7yqO3/xmkBiNl7d3/J1++2+p7QE2ZBeFfIVWJ2t79H1vHGMQ16teJ7+r3m+PghiQAAACfSURBVPzO/wE7R/xt2nv9Gvk5JZASWE4CMcdmXSX+7j1fKYFNlkB9LtQ/b7JMpj17grxpUlmT7wBEBZF37txZVhLZEk1+3vOf//xSNDW9/TXpyGxmSiAlkBJICaQEOpBAgrwOhNrXJXkvmDZh1gifevf/YOD6akveJyWQEkgJpARSAimBYUkgQd6w+iNbkxJICaQEUgIpgZRASqAVCfw/RWDJ7qZuex8AAAAASUVORK5CYII=[/img][br][br]Which is the distorted image? How can you tell?
Is there anything about the pictures you could measure to test whether there’s been a distortion?
[size=150]A [b]dilation [/b]with center [math]O[/math] and positive [b]scale factor[/b] [math]r[/math] takes a point [math]P[/math] along the ray [math]OP[/math] to another point whose distance is [math]r[/math] times farther away from [math]O[/math] than [math]P[/math] is. If [math]r[/math] is less than 1 then the new point is really closer to [math]O[/math], not farther away.[/size][br][br]Dilate [math]H[/math] using [math]C[/math] as the center and a scale factor of 3. [math]H[/math] is 40 mm from [math]C[/math].
Dilate [math]K[/math] using [math]O[/math] as the center and a scale factor of [math]\frac{3}{4}[/math]. [math]K[/math] is 40 mm from [math]O[/math].
Here is a figure.
Dilate the figure using center [math]P[/math] and scale factor [math]\frac{1}{2}[/math].
What do you notice? What do you wonder?[br]
Here is a figure:
Dilate segment [math]AB[/math] using center [math]P[/math] by scale factor [math]\frac{1}{2}[/math]. Label the result [math]A'B'[/math].
Dilate the segment [math]AB[/math] using center [math]Q[/math] by scale factor [math]\frac{1}{2}[/math].
How does the length of [math]A''B''[/math] compare to [math]A'B'[/math]?
How would the length of [math]A''B''[/math] change if [math]Q[/math] was infinitely far away? Explain or show your answer.[br]
IM Geo.3.1 Practice: Scale Drawings
Polygon Q is a scaled copy of Polygon P.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAT4AAADDCAYAAAAbQ31DAAAgAElEQVR4Ae1dB3QVx7kmLycnOXlJIMmL47ycHPPy0l2w49jpwXEBXCFuuGCDux3bAdu4YyMb3LAdbEy3QfSOEV1IAomqjirqoA7qHVDlf+ebe1dPuuhe3bK7M7v7zzn33Hu3TPn+2W9n5pv5ZwhxYAQYAUbAYQgMcVh5ubiMACPACBATH1cCRoARcBwCTHyOMzkXmBFgBJj4uA4wAoyA4xBg4nOcybnAjAAjwMSncx0oLi6msLAwwjcHRoARUBMBJj6d7TJixAgaMmQIxcbG6hwzR8cIMAJ6IcDEpxeSRDR9+nQaOXIkE5+OmHJUjIARCDDx6YQqWnhDhw4VXVxu8ekEKkfDCBiEABOfDsA2NjbS8OHDafbs2SI2Jj4dQOUoGAEDEWDi0wHciRMn0tixY3tjYuLrhYJ/MAJKIsDEF6JZtmzZIrq4aPVpgYlPQ4K/GQE1EWDiC8EuILthw4YRyK9vYOLriwb/ZgTUQ4CJLwSboHuLsT3M2+v7AfFNmjRJHAsher6VEWAEDEKAiS8EYCdPniymr2AKS98PiA/z+XCMAyPACKiHABOfATbhrq4BoHKUjICOCDDx6QimFhUTn4YEfzMCaiLAxGeAXbCCg9fqGgAsR8kI6IQAE59OQHI0jAAjYB0EmPisYyvOKSPACOiEABOfTkByNIwAI2AdBJj4rGMrzikjwAjohAATn05AcjSMACNgHQSkE9+9UYU0ZF4CfxTD4MoNWXS6q8c6NZlzyggEgIB04vtheCo9GFNEYUnl/FEIA7yMjta0BVCV+FJGwDoISCW+9LrToqX3WWaVdRBzQE4z3HZZU1DngNJyEZ2IgFTiW5FXK4gvsbrVidgrXWa0+N5MKlc6j5w5RiBYBKQS39TDpYL4zgWbe77PMAQuDE+l8XsKDYufI2YEZCIglfhu2JZLv1ydLrP8nLYXBEZvy6UR6zO9nOXDjIC1EZBKfD9cmkoPxBRZG0Gb5v7FI6X0jYVJ1NrZbdMS2qdYcIgbEREh/D8uW7aM0tLS7FM4g0oijfjSa13CxhwWNgwybWjRrsp3jb8mV7OyGxqSxt4dHh4uvIBfdNFFvT4hNUe4xqZs7dilEZ8mbCRUsbChYhXKdCu7IEAO6iKAbU09N6/Hf3aN5ttm0ojvBbew0cPKhm8LSTwLZXdaIiu7Ek0QdNIgPrhH4zAwAtKID8LGL1jYGNgqihz90bJUujOyQJHccDb8RQBjfNzi842WNOK7YGkqTYhmYcO3eeSeHbM9jy5dx8quXCv4lzq6t3FxcQRxAxtgYa9nDt4RkEJ8mrDxacYp7znjM9IReOlIGX1tQSK1dLCyK90Yg2QALTztgx3+2AO4b8CkEN9y94qNeBY2fFtH8tnVBXWulTVsJ8mW8D95EB7G9rir6xszKcSnCRvd51jZ8G0euWez688I4sOLioO1EMCez7y9qXebSSG+67fm0s9X8YoN72ZR5wyU3dcSytTJEOfELwQwxsfE5x0qKcQHYeN+Fja8W0WhMz9edpRu383KrkIm6ZcVrNrwDDgGgQMb3nMYGAHTiS/NvWLjExY2BraIYkdv3J5HF6/NUCxXnB0NAYzljRs3TixXCwsLoylTpoiVHCNGjKCBSFG7z+nfphOfJmwcOcUrNqxQ+V6JL6Ovzk+kZlZ2lTQX5uxBzNDG9PAby9g4+EbAdOJ7/pDLFVUXL9nwbRlFzsIZKcb5WIFXxCCcDV0QMJ34WNjQxW6mRXKswaXshufWmJYmJ8QIGI2A6cT3g6WpdF8UO7g02rB6xo8W38vxrOzqiSnHJRcBU4lPEzZmp/OKDblmDyz1nyw/SuN25Qd2E1/NCCiMgKnEt8y9YuPwqRaFIeGseSJw8448+tUaVnY9ceH/1kXAVOLThI1OFjYsVWNejS+jr8xLoCZWdoXd4ioj6flDE/kTAAYbCtVSmk0lvut4xYalCE/L7LpCl7J7iFvqApL3Ul9m0guA9PCSmBRzs1adlPg2lfh+sDSF7mVhQwnDB5KJHLeyuySHlV3g9ti+cbSmYHEgEDr62uW5c+m6iN9QU0eDMjiYRnza5uH/ZmFDGeMHkhEou9iAyOmh/myteIhTa+KdDoXf5T94MlpgllWf6vc9Rl9oGvEty60RE2EPnWRhw2ijGhH/8BVpdOtOVnaTqw+Jh/h0F2/C5G89q2wrE5jtKtns7y2GX2ca8T13qEQQXwcLG4Yb1YgEbtmZx1sFENG6wiV0d+Q1RkBs6zjR1V2U/ZEyZTSN+K7bmsMPjjJmDzwjryeUiRdXY7uzvTG/m/ISvZn4bOAAOvyOCdGjaVrC08qgYBrx/deSFBq/h1dsKGP5ADOyvrBeEN8Bhw9VPLJvLK3OXxQgenw5XhYTY25SBghTiE/z5Ptx+kllCs4ZCQyBvMazgvgWH6sO7EYbXV13ttotbByxUanMKcoyTdltrzcnwUFSMYX4sMAdqqDTWwuD2EL507Ahtg1wakisOiCIr62LXaoFWgc0ZTezTg1l1xTi04SN9u6eQPHi6xVC4Kcr0wjL15wa1hZ8TndHjnRq8UMqd2VbqXhp7CzZFFI8et1sCvFdy8KGXvaSGs9tO/PpZw7eK2VmylR6I+EZqTawcuJQdhdmf6hEEUwhPggbd7OwoYTBQ8nEtMRyMWTR0N4VSjSWvffhvbeysBGC9SZEjaLXE/4ZQgz63Wo48eW6lzt9lMbChn5mkxPTxiKXshtX2SwnAxJTrTtbI7pqKTUsbARrBii7D0bfGOztut5nOPFpwsb+Sl6xoavlJESW71Z2F2Y7T9lNqNrvEjY6uR4HW/WW5X4mMFRhza7hxDfFvWLjLAsbwdYXpe6DsgubOi2syV9M43nFRkhmP1AZJYgvsy4lpHj0uNlw4rs2glds6GEoVeKAuIEtJ50WZiS/QG8otPLAivhX9Cq7G6Vn33Di+/6SFLorkjeklm5pnTIwdlc+/c/KNJ1is040D8XcQqvyF1onw4rm1KXszpKeO0OJr6DJNdv/QxY2pBtarwy84VZ26x2k7Da017mEjerDesHo2HiEshv/lPTyG0p8S90rNpyoAkq3rEEZ2HTcpezuq3COsht/KlYQXysLGyHXqjcSn6EHo8eEHE+oERhKfFMOulxRneniFRuhGkqV+wvdrfj5WVWqZMnwfKCLe8+evxuejhMS0JTd5o5GqcU1lPj+HpFDv1ydLrWAnLj+CEDZ/ddB5yi7byc9p5RLJf0tal6MmrKbUZdsXqIDpGQo8bGwMQDiNjiEl9mobbk2KIl/RYA7JRY2/MNqsKsq2krEsMGO4g2DXWroecOI73hzu1jeNOsor9gw1IISIsfm4hetcIayi8m2UCLhcp6DPggAzwVZH+gTWZCxGEZ8mrAR66BB8CBtYLnbpie51uzWnbX/mt3Dp/a5hQ3niDlGV8gHokfTa/FPGp2Mz/gNI77JbmHjNAsbPg1gxZObHaTsrsxbQPfuudaKZlI2z/BwA/KTGQwjPpewkSGzbJy2QQgUuZXdzzLtr+yGJU2haYp4FDHInKZHG547R7SiWzqaTE9bS9Aw4oOwwa6oNJjt9w1l95kDxfYrmEeJ4E0ErT4O+iGwv3KPIL702iT9Ig0wJkOIr6TFJWx8cLQywOzw5VZB4NdrMuj6rfZWdtEiYWFD/xpZ3upSdrcXr9c/cj9jNIT4lufVCkXXSbP7/cTbNpfdsbuAfrL8qG3KM1BBDp2McXXJOuV1yQbKlx2O4YUyP+t9aUUxhPg0YaOtk1dsSLOswQmHJVWIl1utjZXd5Xnz6N491xmMpDOjfyB6DL0a/4S0whtCfBA2frWGhQ1pVjUh4S0nGgTx7S237zSP6Yn/YmHDoLoEF18TokcZFPvg0RpCfN9jYWNw5C1+hTZB/dOMUxYviffsY8rFyrz53i/gM0EjoCm7rZ1yXpy6E195a4doCbyfysJG0LXCIjf+x/xEemq/PZXdts4WMb6XVH3QItawVjb3V0YKfGWt2dWd+Fblu4SNvbxiw1o1MYjcXrI2g+Bh247h8Km9LmFD4lwzO+Kqlam8tVjgu614nXbI1G/diQ9eOzDHq7Wz29SCcGLmIwDP2v+9zJ7KLtwn3Rd1g/mgOihFKLvzst6TUmLdie8aFjakGFJGom8nu5TdmjP2W7P7ZuIzvMeGwZUKk8NfOfK4wakMHL3uxPe9L1JoPG8ePjDaNjsa4VZ2Y8rtN8/t/qgbaAULG4bWWCi7wFlG0JX4Tp7uFN3cd1nYkGFL09Msdq/QmZ1uL2X3TFcbCxsm1KalOZ8KnCEkmR10Jb61hXWC+GJsPLfLbAOpnt7XFiTSE3EnVM9mQPmLPxUnHkjZ7tEDyrQFL45zK7sy9tnVlfg0YaO5g4UNC9bDoLJ82bpMGrnFXsou5pjdHyVvcm1QhrDgTWWasntirem515X4rtmSQ1i8zsE5CGA898LwVFsVeFrC0wRxg4PxCAhlN/Nd4xPySEFX4vsuCxse8Nr/7wy3slt9ptM2hb0v6npakTfPNuVRuSDYz0SGsqsb8aHiY/4eCxsqVzP987at2LVmN9omyu7Z7jNifC+x6oD+YHGM5yEAb8wylF3diG9DkWujabs8AOdZiA8MiIDme/GjNHtsKgXCQ/eLhY0Bza37wV5lt6tV97h9Ragb8WnCRpMDhY3i4mIKCwvr/URERFBcXJwv3G117usLk+ixWHsou0tyPqEJkveDsFXlGKQwcRW7xYsms87ccWLdiA/KnlOFjS1bttCQIUPO+wwfPpzS0uy/DeMV6zPpr18eG6SKW+P06wlPEdxRcTAHgbLWE4L4tp5YY06C7lR0Iz4IG/c4dMXG5MmTBemh5YeA7/DwcHHs8ssvN9WgMhK7L6qQLlhq7hvbqHJiRzU4IOVgHgIYWphrsrKrC/Fhf1UnCxsjR46koUOHnldTPAnxvAtscmBmSqWwf5UPZRct32uuuYYaGxt7S60dU6VV3NHT7hY29vfmkX8Yj8CkmJvp5SOPGZ9QnxR0IT5tn9WoMvut2eyDldef6OaOHTv2vPPTp08Xrb7Y2NjzztnpwPbiRkF8g9n/oosuImCCAALEUMDEiROVgSK5+pAgvqaOBmXy5G9G0MuYNGmSeLkMGzZMfE+ZMkX0PvyNQ9Z1byY+S5hCZGbQhfi0PTYa2523YgOtFRCf9kD3NR7IEOe0LnDfc3b6XeZ2PvvhIMouuv8gOwS0kvFRKXxxbDZhLwirBW1YBb0OYIqeBr5R90CCqrSoveEKQQnd3dNdbd4u0f24LsQHYeM3Dl2xoVU6z1adRoiqPdy61yB3hN9clEQP7zvuM3q08vBwYtxzxIgR/bq9Pm806eRr8U9SWOJkk1LTJxmt/uEl6/mC1UQ37WWjT4r6xxLrVnaz6r37dkTZMHPCM2jHPcvueZ3nf12Ib9gXyXRPVKFn3I74j64a3qzaFBZ8o8uBY3jIVX/b6mWkKzdk0Z83D67sangFWlH1yqeveMZH/t1SKzaAIeqZr5eIhjdIUNVQ2qvsel+zi4YFyur5PKF8wTQuQiY+zNuDsPGeQ11RodLBIH0/IDwYRMWH26jKPyG6iL6/JMVn9Ki8wAYf1R7Erp5O0d1KqLKOsKENpXiSQV8jaIQx0FBM3+tk/0ZX97PMd3xmA89Y356V1qvqe8xnBH1Ohkx8W93OKPc4XNgA+Pg4iez61COxVBEvwKrTA6/ZRSXFeBO6ZhiDgsKrUkipOeISNtrrVcqW17xg2ABEMJCo1vcm1ElcpzrxPRRzC710+NG+WT/vN16Ys2fP7j2Oll4wrT1EEDLxPX+oVLT4Gtrt5368F2EvP7RK1dcYXi61/eEdJS5ld6AXoKbggvAQtC4a8FMlYOkUXKFbJWhje4PVPa2Oqk58mDQ+2ObtIDmtHFq5gm1ohEx8f9tyjH6z1pmuqGAEvE19dTWs8iCFmk9tW9FZAyi7GA7wfDNjKAAfVQI8hIQlTVElO4PmQ6t7g708NILQCGPQiCVdoCm7Z7pOe82BplbjAtSnUOpPyMQHYeNehwob2hiLV0s57MS3FifTpL39lV209vDw4btvwJt6sIe27/VG/747cqSlNg/3l/hAFng5qzam6mnP2IpdYqghu977Ek+UGYSHeoNub7CtPaQdEvFhC0knCxuYkOvZkvE0qJP+X7Uxm/6wKdtyRe451yMeuvgq6ziWQGsHhDbYy0MT3zxfPKoZqbTluLCBr312UVY8b/iE2oINifi0cZ3IUmeu2IABBhtjUa2CGZmfiTFFhDXbVgtHaxPEQ9doEWED+GotPl8tORAFyDGULqGZtoSyOydjptckMaSkzQoIlchDIr4Xj7iEjXoHChterePgE+8fda3ZPeVF2VUVGmweDk/AVgogPJCaN3UcxICJ4qF2Cc3E5KG9t9CLhx/xmiTKhDKH2tpDAiERH4SNix0qbHi1joNP7Cp1KbuRFpvahAXybyU9ZznLad1YrMntG9DSA+mBJKD+WiVg1cw9e671ml0QHoaX9AghEd/Qz50rbOgBvt3iqGjrEGO+s45ayxvznbv/RqvyF1rOHGgBaeSntf4wVxK/0dKzEukBfM0bM9z/ewZtsrKvrr3nPb7+B018Z7p6RCV/36ErNnyB6uRzeBk+GFNkKQgwtoS9dK0aQHAYx8OYM0gPa3NDHQOTgcU+t7J7rD69N3ltsjvKpedYZdDEt9vdrcE3B0ZAQwCq7tUWUnbTa5OEsNHQXqcVwdLfmuhhRdFNU3a3F6/vtQFaeiiL3nNlgya+V+LLRIsPTkg5MAIaAg/tPU5o9VklYBtJOMK0U9C6v3qThRkYXR9xMc3JmGF4UkETH/ZYYGHDcPtYLgGs3MDczpNtA6/ZVa1ALx1+hN5Ofl61bIWUHxAexvgw3me1Lu/De2+lqYcfDqn8/twcNPHhrY69FjgwAn0R2F3aJIjPKkMgd+z+C63OX9S3CPxbIgJYNjh+z98Nz0FQxNfRfc4lbBytNDyDnIC1EEBLDy2+DyxSN1zChjrOEqxlbf1zG547R4y5tnef1T/yPjEGRXzYWwGVG/O2ODACnghg9cb90eoru5l1KbYSNjztYMX/+yp2CpvkNBjr+CQo4ns9oVwQXy0LG1asW4bn+U+bj9HvNmYZnk6oCazMX0BYLcBBHQRKWooE8e0o3mBopoIiPggbl/CKDUMNY+XIH913nOCpRfWA5VEzkl9QPZuOy98NWy/xuWZXD0CCIr7vsLChB/a2jePjdJeyW9nWoXQZb9/1Z1qTv1jpPDoxc4/svY2mHnrI0KIHTHzd51jYMNQiNogcXpitMAYMYSPBQq6obFA1/CoC1k2PjzR2a4KAiW9vRbOo1FaZruAX0nyRrgjAOwuIT+XljNn1R8VYUn17ra5l58hCRwDecvBS6uhuDz0yLzEETHxvJrqEjZoz1pig6qXcfNhgBLDjmsqeuTF3D5NlOaiHgKbs5jZkGpa5gIkPm4dfsta4DBlWUo7YVAQggF2xQV1lF66oZiZPNRUTTsw/BEpaCkWLb2fJRv9uCOKqgIkPwoYV5mgFgQXfoiMCj8eeoG8uStIxRn2jGrfrj7Sm4HN9I+XYdENg1NZLB91nN5TEAiY+16x8a/lbCwUgvjc4BGZnnBLjfPDRp2LAGFJi1QEVs8Z5IqJH942lFw5NMgyLgIgvrlITNpy5x4ZhVrBhxNrqnp0l6q3uyWlIdwkbZ2tsiLw9ivR28nOEne+MCgER31vJFeItXs3ChlH2sE28qCPoHbynoKPatQWfE+aKcVAXgWW5c8XLqbPHmB5DQMR37dYcunQdCxvqVhe1cnbB0lS6R0EPPq/GP0HvpLyoFlicm34IaPvs5jUaI5AFRHzfZmGjn3H4j28EMANgxHr1XpRjd/6B1hZ84TvzfFYqAsVuZXdXySZD8hEQ8bGwYYgNbBvpk3HF9I2F6im7EDaSqg/aFne7FGzU1stobua7hhTHb+I7eLJFjNk4dfNwQ9C3eaRzMl3KbnmrMeM0wcCHSbEgvjoWNoKBz9R7Hts3jp4/NNGQNP0mvpkprs2iqyy2WbQhqHGkfiEQXe5as7tDIWV3feFSMVXCrwLwRVIRmJH8PN1lkLLrN/HdsC2XhQ2p1cB6iWNZI4ZH3lVI2X0t/il6N+Ul64HpwBwvz5snWuddPfovj/Wb+L69mFdsOLDuhVzkC8NTafwedfZmuW3H1bSucEnI5eIIjEcgtmK3IL78xmzdE/Ob+PDmnnWUV2zobgGbR3hthFpToDC+l1x9yOao26N4xc0Fgvh2l27WvUB+Ed+RU60uYaOMV2zobgGbR/j0/mL62oJEJUqJlgOIr/4su6JSwiB+ZGL0thE0L/M9P64M7BK/iA+z79Hig581DoxAIAjMzaoSdadMAWV3Y9EyglLIwToIPLbvH4as2fWL+MZsz6PLeMWGdWqLQjnVHNeqoOxOS3ia3kt9WSF0OCuDITAz+QW6c/ffBrss4PN+ER+EjQkW2C4w4NLzDYYjgJ340Ft4J0X+Hsy37byaMJ2Fg3UQWJE3XwxPdJ/r0jXTfhGfEDbSWNjQFXkHRfbjZUfpbgWUXYzvpVQfdhDy1i9qXGWkIL6CxmO6FmZQ4kuqdgkb2ECGAyMQDALXb82liyVvR1rYlCMeoIb2umCKwPdIQuCEW9mNLP1S1xwMSnwfprm2CmRhQ1fcHRXZswdK6Kvz5Sq7m4tW0OOx/6AlOZ8Q9nTAA8XBGgiM2XY5zc96X9fMDkp8t+xgYUNXxB0Y2YJsl7JbKlnZfXr/PQSX8+jyap8JUaMIogcToroV8/HY23XfZ3dQ4mNhQ90KYZWcaZ67txfL98bc3NFIOQ0ZFF2+jeDsEn75/hl3N8FVlUaG+GZCVKd2zUyZSnfu/quuGRqU+CBsoLvLgREIFoF6t7I7M6Ui2CgMv6+po4GO1adTVNlWCs+dI3ZgeyruLrpt5++ZEA1H33cCK93Kbs+5bt8XBnDWJ/Gl1rSJqQgsbASAKF86IAI/WQ5l13rjamghYvPxPWURtDTnU5qR/AI9GXcn3brjqn6E+ED0aO4yD2j50A/ur9wjsIZApVfwSXz/Tnf5U2NXVHrB7dx4Rm3LpV+tybANAC2dzZRVn0qRpVvE+ODbSc/RE7F30C07ftePEB+MHsOEGKLVNW/MwFqv4JP4xu7K5xUbeiHt8HimHCyhr8xLsD0KbZ0tlFmXQlhY/8Wx2fRW0hTC4PzN26/0IMQb6Q0WVfyuDzduu4LmZ33g9/WDXeiT+IZ9kUwPxBRRQlUrtXX1DBYXn2cEvCKw6Fi1GDYpaWn3eo2dT5zuahMtROwh8fmxf1NY0mSxbvim7b/tR4gTY26iNxKfYZXZozKgNT318MMeR4P/65P4NNfhEDjw+WF4KmEy6pRDJbQkp4YwufkME2Lw6DvozgPurQu2FTc4qNSDF/VM12nKrk+jnSUbaXH2RzQ98V/CQzRaOH1V5kkxN9Obic86lhChvt+x+y+DA+rnFT6JD2ocWnur8mtpelI53R9dRFdvyqbvfZEiiFAjxB+FpxLGcJ4/VErhuTWUXNNG7d3cQvTTBo64rKHdtWZ3hsLKrkqGaO8+S9j4fEfxBlqU/aEgPewFPGbbiH6E+FDMLYIs7T4PcWX+AlHunnP68IpP4vNWEerchLjSTYj3gRA3nk+IWKM5ensuTT1cSsvzagkqcWfPOW/R8nGbIzB8RRrdFWk9ZVcls3T0tBM2TEILcWH2LDFO+PDeW2n0tsv6E+LeW0V3Gkq0HVaqHKiMEuUrbMrVxRxBEZ+3lLUWYi8hRhUKQvyuRwsRUxtu3J5HLx0ppRV5tZRWe5q6zjEhesPVLsdh81+sTrdLcZQqR2dPJ2HzbYgqC7I+oGkJ/yS0BkdtvbSXEK+PuJhAkhBcMFfRSoRY0lIkyoFpRXoEXYnPW4Ya27spvqqVQIhvJpbTfVGFdNXGLPIkRLQIbt6RR6/El4nudUbdaeIGojdUrXccQyEYHuFgHgJw5wTPJljkj/Wur8c/RZNibqIbtl7SS4j4jW70W0nP0bLcz5QlxJu2X0ELsmbpAp4pxOctp80dLkJEqw+EeK+bEId5tBB/ujKNbt2ZT6/Gl9GagjrKrDvtLUo+rjACn+fUCOIrdqiyq5JpMFaGCcFoQaGF+Gr8k/RgzI10XcTFvYSI1uKj+8bS28kgxLkUW7FLqnOHJ2PvpBcPP6ILjFKJz1sJWju7Cft8nE+Iyf1ElZ+tSifMNXw9oZzWFdZRdv0Zb1HycQUQOHzKtSn91hOs7CpgjgGzcI7O0fHmPIou2ypElVeOPE4PRI/pJUMozaO2Xiam4mDfW2wBid3QzPB2g21B79Bpza6SxDegRYjE1BmozCDEN9wtxN9tzCLMN9QUZnz/cnU6jduVL65ZX1hPOQ1MiN4wNfN4U0e3sNPbyequ2TUTD6uldaI5n2LKt9PiYx8TCHFC9Oh+hIiNgbBHBtzFw3MynIjqSYir8heK9EDOoQZLEZ+3wmLqTFJ1m1COQYj3RBUSCHHo5/0J8ddrMuiO3QVias7GonrKazzrLUo+bhACGLa4k5Vdg9CVEy2WlO0t3ykmZqPLfH/UDf0IEf70sHoFXlbgcABrb3FPoOHgSZeyW9SUF+it511vC+I7r1TuA5g6k1LjIsRpbkK8ckN/QvyP+Yl0ydoMMc0iLKmCNh+vpwImRG+Qhnwc4tXPV7GyGzKQFoigtKVIjAtijiFElfuiru9HiJikjRUZmJyMeXqYsgL11lsobTku7ocHnVCDrYnPGzjd586JKTSYWygIcU8heRIi9oLFznLj9xQSumZbTjRQYRO3EL1h6u/xFw+zsusvVna9rqz1BMVVRApvN3AC60mIUG8hZGBMD91btPRAeghY4rcw+8OQoXEk8flCDVNoMO1mWkK5ID0Q4nf6dJm/vjCJrlifKabkwL8cBuqPNztz/RZrD0kAAAQhSURBVKkvHL2dW5rrUnZPMGbeIHLs8fLWEtENDs/9TKxXvj9qVL8WIkgPPhJfOvJoyBgx8fkJYVb9GVpdUCcUZLQCf+tBiN9clCRajdiG893USsKaVJ62cT64mM8JASqCld3zweEjAyJQ2VZKB09G0/LcuWJ5Xnpt0oDXBXKQiS8QtAa49ljDGVpb6J0Qv7U4ma7amE0TY4ro/aOVhI21Sx08jw1zN0F8b7GyO0Bt4kNmIcDEZxDSUIw3FNWLLjP2lEULEfuXaNNuoDj/YVM2PbT3OM1KO0m7ShupTPJmPAZBcV60mH8JdZ0DIyALASY+k5EvaDpLm4rqxUoVEOIV6/sTIpbx/WnzMXp033H6OP0kRZY2UUVbh8m5NDa523bmE8iPAyMgCwEmPlnIe6Rb1HyWvjzeQJhSc9eeAkGI6CZrLcTvL0mhv355jB6PPUGzM04R9kE5ebrTIxZr/H35SJkolzVyy7m0IwJMfIpbFeonlOMZyRViriEU5b6EeMHSVBq5JYeejCsmOI6NLm8i1fdIWZZXK4iP1XDFK5+Ns8fEZ1HjQiDBPrXvpFSKaTeXexDiheGpdG1EDj29v5jmZlXR3opmqjmjRgsRnrvRksXcSA6MgAwEmPhkoG5gmuWtHbSzpJHeS60U3m5AiP+5OKm3ywznsNg+4NkDJbQgu4qw2Xft2S4Dc3R+1HBCAeJDt54DIyADASY+GahLSLOyrYN2lzbRB0dPii0EPAkRzmGxfQB2Q8PGQNgjo77dOEKEI4nbWdmVUBM4SSDAxOfweoDxwKiyJvoo7SQ9GFNEghAX/X8LEc5h4TkZTkThTw+upeBYNtQA7zn/y8puqDDy/UEiwMQXJHB2vw3jgTHlzYRN5SftPS7mIWJ1iqYyw8sKHA5g7S2WoWFFBiYn+xvgVBZxcWAEZCDAxCcDdQuniY2m9lU00ycZp+jhfceF+6++hIj5eZinhykrUG8hZGBMzzNgPTSIj5VdT2T4vxkIMPGZgbID0sD2kXGVLTQns4oeiz1Bv9+UTX0JUXMOi5YeSA/uwkB8mLvIgREwGwEmPrMRd1h66P4ePNlC87Kq6Im4E/THzdn9VOawpHKHIcLFVQEBJj4VrODAPKD7C6GEAyMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFQEmPqnwc+KMACMgAwEmPhmoc5qMACMgFYH/A/6rHTCL3GkGAAAAAElFTkSuQmCC[/img][br][br]The value of [math]x[/math] is 6, what is the value of [math]y[/math]?[br]
What is the scale factor?
Figure f is a scaled copy of Figure e.
[table][tr][td]We know:[br][list][*][math]AB=6[/math][br][/*][*][math]CD=3[/math][br][/*][*][math]XY=4[/math][br][/*][*][math]ZW=a[/math][br][/*][/list][/td][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWkAAADRCAYAAAAOlUPiAAAgAElEQVR4Ae2dCdxXU/7HESolQtNiH2oijFIaIcKoVNYsaaxZo5QtoWYKM9ZQodI0RaXFki2EsVNDJlMpEsoSWkZpsTTO//U+/udxn/v8nuf3u/u5936/r9fvub/n/u4993s+59zP/d5zvuf73USJCAKCgCAgCFiLwCbWaiaKCQKCgCAgCCghaekEgoAgIAhYjICQtMWNI6oJAoKAICAkLX1AEBAEBAGLERCStrhxRDVBQBAQBISkpQ8IAoKAIGAxAkLSFjeOqCYICAKCgJC09AFBQBAQBCxGQEja4sYR1QSBtCHw0ksvqZdffrngJ211sUVfIWlbWkL0EARSjsAnn3yiNtlkk4Kf3//+9ymvXXLqC0knh71cWRDIPAKPPfaYJm22Iv4QEJL2h5ucJQgIAkUQ+Pe//6223XZb9ec//7nIkfJzVQgISVeFjvwmCAgCvhD473//q/bff3913HHH+TpfTvoVASHpX7GQb4KAIBASAmeddZZiHBqyFgmGgJB0MPzkbEFAEHAhcOedd6ptttlGMdwhEhwBIengGEoJgoAg8P8I4IKHh8c//vEPwSQkBISkQwJSihEE8o4ALnhMFF522WV5hyLU+gtJhwqnFCYI5BcBxqAPO+yw/AIQUc2FpCMCVooVBPKEABOFu+66q0wURtDoQtIRgCpFCgJ5QsAsWNltt93U4YcfXu4DeYsEQ0BIOhh+crYgkHsEmCxkwUqhj0wgBu8eQtLBMZQSBIFIEID0jGXKpJxIPhEQks5nu0utLUcAgsbXGEuUjywKsbzBIlRPSDpCcKVoQcAvAkzCsSgkbbJhwwZ13333qYEDB6oXX3wxbepbqa+QtJXNIkrlGQFW6rEgJG0r9lauXKmaNm1aLlTp4MGD89yUodRdSDoUGKUQQSAcBPCGYEGIicuMRW27rF+/Xi1fvlz17du3TG+j/2abbaY++ugjtXr1arVx40bbq2KlfkLSVjaLKJVnBCBqGxaFLFu2TM2YMUMNGTJEnXPOOerQQw9VzZs3V02aNFGNGjVSderUUdWqVatAzIagC21r1qypdthhB4W7XrNmzVTr1q1Vp06d1NVXX60eeOABNXv2bPXDDz/kufkr1F1IugIkskMQSBYBVu4xcRiXrF27Vr311lvq/vvvV71791bt2rVT9erVKyPfrbbaSu2888469OiRRx6pTj31VNWzZ081YMAAddddd6nx48erZ555RhOtm5gph3RajzzyiBo1apT629/+pq644gp19tlnqy5duqg2bdpo0t9+++3LrkcZjRs3VieccIK6/vrr1aRJk9TcuXPjgsO66whJW9ckolDeEYCkos5k8sorr6jrrrtOtWrVqhw51q9fXx199NHq2muv1Tp8/vnnnprj5JNPLiuvVq1aavLkyZ7Of+edd9TIkSPVBRdcoA444ICysgz5d+7cWY0YMUItXrzYU7lpPlhIOs2tJ7pnDgETRS5sv+gPP/xQDR8+XHXt2lUZq9UQ8pVXXqkmTJigOCYM6dWrl9p0003Vd999F7i4devWqTfeeEPdc8896vzzzy9H3CQV4EHDkEyWh0iEpAN3IylAEAgPAYY5wposZAiiX79+6sADD9QWKePIl1xyiR77fe+998JT2lXSX//6V8WEYVSyYsUK9cILL6jbb79dMfyClc2wSrdu3bSVvXTp0qgunUi5QtKJwC4XFQQKI0C6qSApp7AoR48erVcqmiECyhs7dqz2sCh81XD3Rk3Sbm1nzpypH0ZMaFLnunXr6rH1t99+231oKv8Xkk5ls4nSWUUAK9rPpCHW40033aT22msvTVQtWrRQN9xwg5o3b17sUMVN0qaC//vf/9TDDz+sunfvrpjshLCZ5HzqqafMIancCkmnstlE6SwiwNJviIVx6VIFaxGPDKxHXvmZcHv22WdLPT2S45IiaWdlPv30U71is23bthpTYqDwhpHGsWshaWfLyndBIEEEzKRhKXE6sA6xEiH1Y445RrvPMVZrg9hA0k4cXnvtNXX55ZfrCVPeNHjjsAUrp56VfReSrgwZ2S8IxIwAaafwka5K8MDo0aOHJuc999xTk3NVxyfxm20kbTB4//33FQuFeLCxfD0tYVSFpE0LylYQSAgBLOhp06bp5eBVEccdd9yhfvOb32iS6dOnj2JFoI1iK0kbrBi3btmypcbxxBNPVEw82ixC0ja3ThHdeC1mNZf5pC0gT5Hq5eZnLGiWgVc2YTh9+vQyb40//vGP2v3MZnBsJ2mw+/7779WgQYP0BOPmm2+u/a3XrFljJaxC0lY2S2lKYXXx6ub8EJynKmustJLlKBsQYPLr4osv1u2Lj/Pdd99tg1pFdUgDSZtKECvklFNO0Rjvt99+elGP+c2WrZC0LS3hQw/3GCar1PCJhbSjXlbsQ105xQMCw4YNUzvttJNuSzw2Pv74Yw9nJ3tomkjaIEVwJwI+ce8wIRvlYh9zzVK3QtKlImXhcbwiF0r0yX6WzIqkE4FLL71Uk8UhhxyinnzyydRVIo0kDcirVq3Si2Igat5cpkyZYgX2QtJWNIM/JehMhbJ3MLbJbyLpQgC3sJNOOkm3HfE00ippJWmD99NPP61DqXIPsSAoaZE7OekW8Hl941NbaLKQoQ4haZ/AJnTaf/7zHx2zg3bj1TvNknaSBvtFixbpkK20x5/+9KdEm0NIOlH4/V8cC7oyIhZL2j+uSZz53HPP6bbcY489rBoL9YtFFkja1J1kB9xnuOwlJULSSSEf8LpVZe/gt7AiqQVUU04vggCr3yAB4jBnRbJE0rTJ0KFDdRttvfXWKokIe0LSKb0zWJmGd4db8J3GDa/Qb+5j5f9kEWjfvr2++clWkiXxQtIM15HdhSh9CB5KYcfSDgNbhj8gaR6oxLeOU4Sk40Q7pGuZQDyF3OyworfZZhsrO3pI1c9EMax044ZnqCNrUipJY0iAAd5IvPnxP98LTYbbghF5HtHZa8aaIPoLSQdBL6FzzaSh0+LgO3nj6ECymCWhhinxsvg9006kgcqilELSZt6EvmwEggYX5z7zm01b4n5sscUWKq4VikLSNrV+ibqYDv6Xv/xFEzNhGOncWCO2d/ASq5jZw8gdSFvhC51VKUbSZkiOfuwU06+d+2z8/uOPP+qIenGtRRCStrEXFNGJYQ46tPMj5FwENAt+JscgBM0y5CxLMZI24Qwga6cwVFcsCqDz+CS/kwiXtjz99NMjV0NIOnKI5QKCgNJR7ripO3TokHk4ipE0xkUhMjbj0mkBiMBmtCl5I6MUIeko0ZWyBQGlFNlTGjRooNq0aaM2btyYeUyKkTTxZRh/dopZgJW2+ZQHH3xQE3X//v2d1Qn1u5B0qHDGX9hXX32lXZgGDx5sfVzc+NGx44qEF91nn30UAfvzIMVIGkvaOZ5rxqixSgutoLUdM1wo0X3SpEmRqCokHQms8RQ6d+5ctcMOO+gOQifhM3LkyHguLlcpCYF77rlHt8v48eNLOj4LBxUjaeZP6Kt4IzH5zTAHbne4jqZV2rVrpw444AAdpzrsOghJh41oDOWtX79eLV++XJ122mnlCJqOT/SuL774Qq1evVqRPVkkOQRoh913310df/zxySmRwJWLkTQqMbzBsAeThWYBS9qGOpzQEq2Q+y+KgEypIWkaklVJfJz+wU6g0vadGMEkFL311lt1iEQmILAuunbtqieYcJxv3ry5atKkiSbfOnXqqGrVqlUgZjpHZR9S25NyCbLYd9991UEHHaR4/YY4CBxz0UUXKSKuYdFMnjxZYZ0LuYfTk/r27avb5dVXXw2nwJSUUgpJp6QqntQ0C8m4h8KUVJA0T1iWOjMjzKsR39NE1B988IGe3afzQowtWrRQNWrUKEes/M/k0u9+9zvVunVrxZJhXLVY+HD11VfrDMe8Ok+YMEET++uvv67OO++8cmVA1GSXYKLq+eefV1OnTtWJSm+77TZ1/fXXa99crt+5c2dFrGLGSQksX7t27Qrl4LDPqrjrrrtOX5Oxwh9++CHMvpfpsl555RWNae/evUuuJxjj8+7u24zZsj9KS5NxYvqPW8x+t4snunC8W1fOTyNJM9xSKJQC9QP7Qqt73ViRKKBWrVoFY7y7j/Xyf8VW8XJ2DMea8StnB6Vz2Lh0dP78+ZoYmcRjKALCJH8a+ppPvXr1dKP37NlTQbrU75tvvvGF5IYNG9SRRx5ZVvaOO+7oezHLunXrNLmPGzdOW/VdunRRZKM2epst+/itX79+imN5IHCuSHkEwIj2WLJkSfkfivzHuKy7b+MJ4faGKFKM558NGTtPdE7ouUkafbAcC0kaSdo8dNz1oZ6F3AXdx5n/Bw4cqO+ZUkjdnFNsaz1JuzsD1gaEESYIxUCq7Hdy0EG0nTp1qkBmYZJxZdc3+7F4scKjEKxnMMeCx6rmWljZhrTNFvcyZrnnzZsXhRqpKvPvf/+7xofs3l4Fa87p+cD/vD26F354LbfY8dxPtKVTIC7uP/Y7SdoYTs59zvPSSNJYzO56Un8emvT/UuXbb79Ve++9t3a3LPWcYseVb5ViR8f8uwGO8VPGTNkCZKHXkrhU4zUWK5KnK7rw2X777VX37t0DW8Z+68C48m677eb3dF/nMW7N2Bvj2LTNH/7whzI8iIvMeCzBg1hCmzc59thj9YPMT71Nn2frhyT8XJNzDPE6z+fhYCxMJyFjQUPelUkaSZq6GC8Tvpu3CPdbTWV1du43oU2fffZZ527f360mafN0p0PwOgZgdN44ZeXKlQqHdTqmSQwKMWM5Qk4zZ86MU52C10qCpAspAlb4ijL52bBhQ03ahHdk6eyYMWNib7tCOka97+uvv9bBd6655hrfl8IAwCCJM/O7m6QhZ0gL4f4zJG0eIlW9yaaVpDH+8DhBCi240T+U8AeHAIY5L7/88hKOLn6I1SQNKUOIcQupjIYMGaKHMcwEH9YhWRrwd4WMbBJbSNqNCQ+wm2++uSwNEW15xBFHaDeluGPyunWL6v+JEyfqPvvWW2/5voSxXuN8Y3STtLGiqYQxkviOsWTIu7IKppWkefDwYGQbNNwvJE/28TAkfgb0oLXpOOYp7uFUz4eycg9ixrMCMsHjoWPHjnqc1QZruaoK2UrSTp3xGeYB16NHD/Xb3/5WY4wnCxYns+JZEd4iWrVqFag6ZijNz6u23wube43xV0NSZhzcSdKQFw+RqiStJE19ufch6qDYjx49Wpf1zjvvVAVVSb9ZTdLUgA4CaAwtmHFpnuZhCQSMxcJEHz7FEN6jjz5qnbVcVX3TQNJu/QlOQ3viv82N0a1bN/XEE0+4D0vd//iy+5kwNBWlL0LSbJ0TiOb3qLaGpNk6SZnrmf8hZ0i6mKSVpKkX2FPfoMJcDO549PGgYj1J83TjqQZwfPhunvBBKs+El5mI3HnnnbUfcVpjK6SRpE3bsTJy2LBh2vqErFlsw/+2DSkZfava4ptOHfzOmxgSxJrlQ1lePAuq0q2U37ge9xdE7LzHeHXHMILASjGQ0kzS1D2oFW2wZi6GpeJBxXqSDlpB5/mkvGF1H6v46JBsaZA0EoKzXmkmaWc9HnroIT3ERNuwvJ2VkLNnz3YeYvX3iy++WLVt29aXjpCxe6KQsd84x6XBHSJ2+z9DzOxzk3dlFU0rSZsHY1jDq3h3gClDfUEkFyTNJBVLrrfbbjsNGsui8djIimSFpE17zJgxQ6/MpIPzIZM2Q1C2CwQHQXkVrFaGNtzkCEHH6VoJ1jwo3G8CkDT73fpVVs+0krSZsK2sXn72b7nlloHXdGSapFmAwRJoc7OzCnD69Ol+sLb6nKyRtAH73XffVX369Cl7uB544IH6zQc3NxuF8ehik2qF9Ib8IHjnEAPHGcuuKne3QuX53cd9UoiIIWl+c5N3ZddJK0lT9zDGo5248JDFISGIZJKkec0wWX25ccgn969//SsITlafm1WSNqAvXbpUu+01btxYkwXDALaFZF2xYoXWLYvZv007lLpNK0mXWj8vxzHH0qtXLy+nVDg2UyRN+E4TeczMrOJYnnXJOkmb9iNGyH333Ve2LJ0l6raMWeNqhbWJj33eRUj61x5w0kkn6bf5X/d4/5YZksYHlzXz3Cgs0Z4zZ453NFJ6Rl5I2jQPE734V7Oqi4fxTTfdZH5KbEvEQfoeFnUYsnbt2jCKSaSMtJP0d999FxpuvMUHXdSSepJesGCBOuOMM/QNwkKUhx9+ODSA01JQ3kjatMusWbN07G3IEa+KJIca8BpikiioENb26KOP1v2ZrDtRBJEPqmNV5xNkiwcnbUKExjQF3IJLcCpAd7C/8cYbq6pqSb/xwGL9RRBJNUnfddddOqA9AY5YfpyHJJ+FGjuvJG2wYIIY7whuLuIlhGXNmvJL2eJ+F4YnxsEHH6zrQV3MB9fENAgGktHZbJnsTYswfmz0NlvWUwQR4zHCima/kkqSJuA9S7YBkmXGCxcu9Fv/TJyXd5KmERmvHjRokF7Oz+slxB2ndOjQQS/ECXJNE7zIEITZEqKAlZm2fwimZXR2bglMZrvuLGhz6my+F/J28dLGvN1RVpBYLqkiaYLcDxgwQG222WbaVYbUUyJKL2UPw4rLApbEASH7DDfGmWeeGdsDHPdO0pMFEeMhYgjCbMmgw4PY9g9JLozOzi3tYLvukLFTZ/M9qGeGebtgKMWvpIakp02bppcOk+2CYQ6RXxEQS/pXLMy3Rx55RMe4rl+/vrr77rvN7si2TGQy7BZUiLRoCMJsg1hhQfXxcr7xcDF6s+WBmRYpRNTMewQRQhyAAwamX0kFSd9yyy26oqwaJBuKSHkEhKTL42H+IzEBfad69eqaLIgTEpXgGsjNGEYeSCbfmAgl9kNYS5Sjqre7XJLu4l2F/jZ43bj1K/Y/E30Ge4KABZX+/fsHzppkNUmvX7++LNkqof9ECiMgJF0YF7OXcUHGRBk2CCtbhinbbJ955hlN0qWuyjPnyTbbCBC6lqxFQcRakmZskRl7xlpJWSVSOQJC0pVjY35hTNB4TmAthS2UjyX95ptvhl20lJdiBHCnZL4iiFhJ0own0uHx4Fi2bFmQ+uXiXCHp0puZYE30rVNOOaX0k0o4kjFHys2jn34J8OT2ECaTg6RSAzjrSPqKK67QnZ3l3SKlISAkXRpO5iiCNkGoZIYJc5yajO1MFIn8ggBR/A4//PBcw8FkMvMVQcQakmb8uWnTpvrmGTVqVJA65e5cIWnvTY4fNUTNJ6xxasYee/bs6V2ZDJ5hEhiAb16FBSzUn/mKIGIFgsyimhuG2WERbwgISXvDyxyNpxALReh7YaQ5woefNGx5FyZPiT9NQo08kzRp1Kh/UI+fxEkaP0RD0ESxE/GOgJC0d8ycZ2AB0weDhj8lIh/lvPjii87ic/edmMwMdeSdpIklxMRhUEmUpPHgMAS9Zs2aoHXJ7flC0sGb3hD1k08+GagwMqHneciDBAEkMEBMsoBAgKb05Pfff19zWxhzFImRNNG+qlWrpisSZMlkStswVLWLkTQZP5gsw53RPBT5HlfGj1ArG2FhJkgTCWX9CnkZGfL46aef/BaR2vPIJEMeRLZInkma4TPutTD85hMhaTJtEAqQSrzwwgup7ZS2KF6MpLlZeAWFlOk03ERmCWwYncgWHMLQA48P+qVf33yzqCUNORnDwMuUYfI0OjNt55mkGeogO1QYEjtJf/PNN8qkQRo3blwYdch9GcVIujKAsHq4kUR+RYCEArvssosmaj8LU5gkatiwoSIGR56EMWh3fsC8kvTMmTN1/wkrFnisJM24M/FlsVScT9w8deYo6iokHS6qH330kY5TzkOMoEFehahv+MfyxpgHMQlzGS7CL9p8zPAa/0PieREz1BFWXtXYSJoxuvbt22uCJouFSHgIeCVpXk2JKQAJyXBH4XbgBiM+Mm99THB7kRkzZuh+zjxAHoQ+hNXs/mBZY5Cx308W9TRiN3fuXN1vTj311NDUj42kzRhoGClpQqt9RgoqlaS5abBq8GE97rjjhKCLtD+BmcijiLeC12wveHhAUCSoyKvkcbiDYS6iLvp5A6usn8RC0iNGjNAdltRGIuEjUCpJG0uHV89dd91VB7ASS7rq9mDeBLIlPZYXIUt9o0aNFBnN8yp5I+mnn35a95Xrr78+1CaPnKR5VcSTgxitQVfehFrzDBVWKkk7q8yQBxYiFrVI1QiQ8RmifuCBB6o+0PXrkCFD9HkTJ050/ZKPfzEA0hYPO0jLkHiXcLjffvttkGIqnBs5SXfp0kXVrFkz1699FVAPeYcfkkYFLB0sapGqEfjuu+90TGC8PhYtWlT1wa5fMU4OOOAAMVBcuGTt33vvvVc/kMeOHRt61SIlaTJMYIFIuqvQ261cgX5JmnkCt9tUuYLlnzIEsAhZfOV1QogVjNwD3Asi2UQAt+I999xTHX/88ZFUMDKSJmgSnZpUOiLRIlCMpLGYyRFpxp9xmTJuQrLqsPS2wSsJwvWaM/Hcc8/V98ITTzxR+sXkyNQgYPJSvvHGG5HoHAlJM/Z8yCGHqCZNmuTGVzSS1imx0FJIGnc7CMZ8sKCFoEsE2HEYSQNwzfPiA7tu3To9J1O3bl0lUR4dYGbg68CBA/U9FeXCvEhI+qqrrtKKk2FFJHoEipF09Brk5wosdGGRhtfoZoRFJfgScwCrVq3KD2AZrilx7zF6hg8fHmktQydpMwYXNGVMpLXOWOFC0vE26EMPPaRvTq8xqPGdxYeWlEoi6UbAxGiJIl+mG5nQSRpvjpYtW7qvI/9HiICQdITgVlL0hRdeqP2gv/jii0qOKLybLDBYXyTFFUknAvPmzdNtGFdI2lBJ2ljRo0ePTif6KdVaSDr+hmPyldWIXq1pNH3wwQf1TU6MD5F0IUBOTB6yrNyNS0IlaazoNm3axKW7XOf/ERCSTqYr9OrVy5c1jbYmawmJl0XSgQA+8hB03CnSQiNpY0V7XZWVjuaxW0sh6WTaZ/78+WqrrbbyZU2jsSHqdu3aJVMBuWrJCAwdOlQTNKun45bQSBorOs5XgLiBsvl6QtLJtQ7xaIjR4XVs2mjMZCLWGS6SXqPtmTJkGy0CXbt21W2U1DxCKCRtrOhJkyZFi5aUXhABIemCsMSyk1dgogr6GZs2CkLwe+21lyYCeRM1qCS/pW1xguAhyoKkpCQUksaK9uo3mlSFs3hdIelkWxV30yDWtNH+ggsu0IRAnkSRZBHA4CRxAwR9yy23JKpMYJI2VnTecrol2mquiwtJuwCJ+d8lS5boTC5BrGmjMmVADBg97777rtkt2xgRuPnmm3Ub7L777urxxx+P8cqFLxWYpLGiO3XqVLh02RsLAkLSscBc5UVYHow1HcZqwpEjR2qSqFGjhiI2MWFlRaJHYPr06eqII47Q2Hfo0EEtXLgw+ouWcIVAJP3VV1/pFVR5SY1TAp6hHoIvLqEPsa7YmgBJ7osISbsRif9/PD2wgMMKhUBGFwwgytx7773VmDFj4q9UTq64YMECdd5552mst9tuO4UlbZMEIunJkyfrii1evDiWOplMD1kPJI7lhKcMNyiB+QmGRMwHPAAKWVVC0oW7n+kv4Gg+hJPk4ReF0FaXXHJJqEUTH4IwmOjfuXPnXAXRDxXIAoURCI5l3RAz+BK6l4etbRKIpFkWedBBB8VSJ8iJWXSIKsuZxrGWqSc3vNtydv9vgBeSNkiU35J1hgccD3U+RP0DVwIkRSEQNF4aYcuyZctU3759yx40LKJhHFzEPwLEXzGeG61atVIPP/yw/8IiPjMQSRPVq3///hGr+EvxJkA9Nx0WUlaF+kEkhSzmyuosJF0YGR7o7r7C0BxWU2UPvMIllbaXNFmUHWYSUueV//nPf6r27dvra+y0006ZNlac9Q7z+6xZsxThZmmn2rVrq8GDB1ufNcc3Sb/99tu6okSDilq4oQAVawgSy2pePupn6ukFUyHpimg5+4zzV7PKz7kvrO8rV67U7XfjjTeGVWTBcgiNSSov+sqhhx5qhQdCQUUt2kl/6Nevn463Am7dunVTc+bMsUjDylXxTdJkqSDzyvr16ysvPaRfzGsrxWEZQdRZFN4W/OQcFJKu2BsY2uBmdL6R8BBkKMltXVc82/8eVqXFscybSfvbbrtN7bfffrqevLJzT0bxhuAfjeTPJIP32WefrWrVqqVxOuOMM9Rzzz2XvGIeNPBN0iTYjGMBi9u65AbjRsuiQNCXXXaZ56oJSVeEDBwhaeeHYST6U5SCyxzXXLt2bZSXKVc2qxS5F7kuZAQpQU55FR5UPLB4cIFJ/fr1FQuE0rrs3hdJ4wtK5QEiasFqxtOBnIl8SGrLtbMo1MuPlSckXbE3mGExSJmPmTSMKlmo0eC1117T/TOJiSgsRCxF+hGfvFnXbquZtwzeNnjrSLP4YrsJEyboTjB79uxI625eWU2nc26jcqOKtEJFCqd+QtJFQCrxZ7B0ewHRZ9gftTXNhBR+t0kJFiOWIxYk9c2yde22mqkvbxVZioHii6TJYUgaoKiF13/GaZ3CGGMcN5rzmnF953XcXd9Sri2WdHmUDBm7H+Tc0PQdHv5RCh4YLVq0iPISJZXNvUK4ht69e+uUXdQd65r+ct999ymyW//4448llWXLQUuXLlVkXccr48QTT9QPoJo1a+rvZHFPy2SgFzx9kTQpzHG/i1KqcpWis7mtpCh1iatsrGg/JCIkXb6FTN8pv/eXSWfwjXpyjYhpWLG2CWmfhgwZosM4EAcbLLD6SdRBH2LhjPvBlmQdVqxYoV544QV1++23a2+MJk2aaJ3RmwU+ffr0UcQOWrNmTZJqRn5tXyTNclUmDqMSLICqZuGxOP0MC0Slb5jlMpZKJ2QcnuXgbIstvhCSLt8CvI3sv//+ZfMY4MhkGrjGEcKAOB5ca+PGjeUVs+y/GTNm6GERrGvihLP7l0wAAA98SURBVKAzH0PckCBDm2+++aZeiffZZ5+FSois+Fu+fLkiAzvBpBiGKkTI6ESwfe4FfrdxVWCUTeuLpFllePrpp0emF6+jkJXTfcp5MWbus0rS1BMioX5gwLYYsQhJO3uH0h4yYOf80GfishJNgKS0rQr88MMP9fDIoEGDFIHumzZtWkbchsDZbrrpptqIwlebzOe4HXbs2FGddtppinCrDIfi5cLKSB6YJ5xwgg5cxAq/xo0b67cM50PBWXadOnW0ZX/++ecrhi+wpNM+8Ve+d3r/zxdJAzQNIWIHAkLSdrSD0QIvA4gHCzTtwpg1Vu64cePUgAED9PJ0CBQj7dhjj1VHHnmkat26tWrWrJl+48PiZYyYNRQQLpEBGaZo3ry5XnhDdDkeALzZsIyeBSZ4iRGBLm0Ptbja1hdJ161bVz/l4lJSrlM1AkLSVeMT969MXkHSU6dOjfvScr0MIuCZpBlnowPG6Qf6888/K8bPCN8oUhEBXieZqPrpp58q/pjzPYxfTps2zXcOQj/wMeHFPYJPv4ggEBQBzyTN+BAdcObMmUGvXdL5LA4gmAzX5MP4VxiB1Uu6uOUHsaqNyRSDDUTNGJ7ILwjwhmGwYXvHHXfEBg2v/DIkGBvcmb6QZ5KeO3eu7vjM9MYhkLLzRuM7LoAff/xx7j9uEgIbJnIEm4/V6NGjK/Qb8PGb1dtrX8dFrHv37l5Pk+MFgQoIeCZp3GTo7HHIunXrCt5oXF8+goGfPsDQRxzCGw4fEUEgKAKe2dZY0p9//nnQa5d0fiE3IFyrpkyZkvvPUUcdVeFhVa9evdzjQt/A/asQib///vsl9bugB+EBFaWbalD95Pz0IOCZpL/88kvd+QmeHYewBt95s5HqJi5/1zjqF+QaTIqZ+AwGo/vvvz9IkZk61yQVNdiQSSguYUUf8TNEBIGgCHgmafwm6fTEBIhLcGkiOeTQoUNz79juxpwVWwSBJ1dbVBlB3NdM0//jx4/X/r1xhu40USJZgi0iCARFwDNJc0HSEkEMIoKAIFARATMkOGnSpIo/yh5BwCMCvkg6ztyGHusjhwsCiSNAXGfeNnEfFREEgiLgi6QPPPBAdeaZZwa9tpwvCGQSgTFjxmiSXrx4cSbrJ5WKFwFfJH3MMcfoNfvxqipXK4QAYTfJNkLUQDNBFnVQ+0J6yL5fEbjhhht0W2zYsOHXnfJNEPCJgC+SJkUPrnEiySKAlwvkjEsixEzUQEi7suiByWqbn6uzyAgvJBFBIAwEfJF037591dZbbx3G9aWMAAgQV5tM6iJ2IUC89X322ccupUSb1CLgi6SHDRsmY24JNzlWNMMbUWcZSbiaqbz8jjvuqNM5pVJ5Udo6BHyR9KeffqoJYsSIEdZVKC8KkQyAHJAIQx1kHyGbugx1JNsDSALLw5PYISKCQBgI+CJpLkx6opNOOikMHaQMHwiYzC2MRzPswRbSJtWWWNc+AA3plFtuuUWTNCtzRQSBMBDwTdLkcSPzgkgyCEDKWGzu1Frsl3HqZNqEqxJPBRdVEUEgLAR8kzSO+pCEuHuF1RTeyiFnHxa0WyBt2kUkfgTWr1+vE7pee+218V9crphZBALdzUyQMBYqEj8CZrjDfWUemkLSblTi+f+RRx7R2EsGoXjwzstVApE0CSnbtm2bF6ysqmdl3h2VWdhWKZ9RZcB+jz32yGjtpFpJIRCIpCdOnKgtB5moSqb5GH9mAhfCxqtj7NixenGLe5w6Ge3yd9UWLVqoCy+8MH8VlxpHikAgkmYGe4sttqgweRWpxlJ4GQIQ81lnnaUflAxxEJ3wzjvvLPtdvsSHAMkEaAPJEB4f5nm5UiCSBqTOnTsrVliJCAJ5RoC5mYYNG0qS5Dx3gojqHpikyRmHBfHkk09GpKIUKwjYjQDJbRs1aqSTC9itqWiXRgQCkzSVbt++vVjTaWx90TkUBLCit99+e7VkyZJQypNCBAEnAqGQNIk/xZp2wirf84KAsaL79euXlypLPWNGIBSSRud27dqJNR1z48nlkkcAK5qVt4sWLUpeGdEgkwiERtITJkwQazqTXUQqVRkCxoq+/PLLKztE9gsCgREIjaTR5JBDDhFrOnCTSAFpQQArukaNGmr+/PlpUVn0TCECoZK0iRshnh4p7AmisicEjBV96aWXejpPDhYEvCIQKklzcSKAid+012aQ49OGAFZ0tWrV1Jw5c9KmuuibMgRCJ+lRo0bpsWm2IoJAFhGYNWuWTh8nS8Cz2Lr21Sl0kqaKJ598svYbJaaEiCCQJQR+/vlndcQRR6jGjRurpUuXZqlqUhdLEYiEpBcuXKgIY9qhQwdLqy1qCQL+EMAfmjUBkydP9leAnCUIeEQgEpJGBzOJOGDAAI8qyeGCgJ0IEDwJgu7Tp4+dCopWmUQgMpIGrQsuuEB36scffzyT4Eml8oMAyZcZ4mBifO3atfmpuNQ0cQQiJelvvvlG7bPPPqpZs2ZKEnMm3taiQAAEunXrpg2OGTNmBChFThUEvCMQKUmjjomSR9xjEUEgjQgMGTJEE/SgQYPSqL7onHIEIidp8DGTLcOHD085XKJ+3hAg4XL16tVlEjxvDW9RfWMh6Z9++knnQtx0000VyTpFBIE0IMA4NOnJCKD09ttvp0Fl0TGDCMRC0uD23nvv6SSdWCWybDyDPSljVVqzZo32h8abg1C8IoJAUgjERtJU8I033lD169fXq7V4jRQRBGxFoGvXrnocWgja1hbKj16xkjSwvvTSS6p27dp6ReLixYvzg7TUNDUInHHGGULQqWmt7CsaO0kDKUTNa2SDBg3U999/n32UpYapQcD49osFnZomy7yiiZA0qBqi3mWXXTIPslQwHQj07t1bLOh0NFWutEyMpEHZEPWee+6ZK9ClsvYhYNxEH3zwQfuUE41yjUCiJA3yhqjJ6iIiCCSBALGhGX67++67k7i8XFMQqBKBxEka7QxR16tXT61YsaJKheVHQSBMBDAOIGiIWkQQsBEBK0gaYFavXq3Dm3LDvPLKKzZiJTplCIF58+ZpDyP622OPPZahmklVsoaANSRtgDXuT/fcc4/ZJVtBIFQEGNaAnPEu+uSTT0ItWwoTBMJGwDqSpoIjR47UNxHpiTZs2BB2naW8HCNw0UUX6b5FdhURQSANCFhJ0gD37LPPqs0220y1atVK4iakoSdZriPZvckUhAUtGb4tbyxRrxwC1pI0Wi5YsEDHT9h8883V2LFjyyku/wgCpSLw4osvqqZNm6oaNWqoe++9t9TT5DhBwAoErCZpEFq/fr0655xztAXUq1cv9fnnn1sBnCiRDgRuvfVWTc4tWrRQL7/8cjqUFi0FAQcC1pO00RUXKSyh3XffXY0YMcLslq0gUBCB6dOnq8MOO0w/3M8991xFliARQSCNCKSGpAGXmL4mOlmXLl3U66+/nkbMRecIEVi6dKm65JJLNDmTj1Dil0cIthQdCwKpImmDCJnIGWMkiUD//v3Vt99+a36SbY4RYLx51113VVtttZUi1dUPP/yQYzSk6llBIJUkDfjLly9XV155pbaY9t13XzV+/PistInUwyMCr776qurUqZPuC6eccoqaPXu2xxLkcEHAXgRSS9IGUpaUG9cqMjrPmTPH/CTbjCOwatWqsvyZe++9txo3blzGayzVyyMCqSdp02jDhg1TO+20k876cuONN6qNGzean2SbQQQeeOAB1axZM209X3311WrlypUZrKVUSRBQKjMkTWOyxNesKDvooIPUtGnTpI0zhgCTx6eeeqom52OOOUbivGSsfaU6FRHIFEmb6pHo1kQ3Y/kvC2F+/vln87NsU4jAM888oxjOYsUgiSIktksKG1FU9oVAJknaIMEr8dFHH61v7P3220/dfvvt4i9rwEnJlglhZxvedttt6quvvkqJ9qKmIBAcgUyTtIHnueeeUya6XqNGjbTbHkvORexEgAnBu+66S7FKEMsZkuaBKyII5BGBXJC0adj33ntPu+3Vr19fVa9eXZ1//vnqtddeMz/LNmEEFi1apAYMGKCHMyBnHqw8YEUEgTwjkCuSNg3N6zKvzQyBQAYnnHCCTDIacBLYvvXWW+riiy9WtWrVUjxA8X/ngSoiCAgCGfPu8NOgznHrtm3bqtGjR6svv/zST1FyjgcEvv/+e8UE78knn1w2ZyDjzR4AlENzg0AuLelCresct95yyy3VUUcdpZcWs1hGJBwEPvroI3X//fer008/XTVs2FDGm8OBVUrJOAJC0q4GXrx4sRo1apT2xd1hhx00key8886qe/fummAkVKoLsCL/8pAbOHCgwm+doaVq1aqpzp07qzvuuEO9++67Rc6WnwUBQUBIuoo+wCv5o48+qqOqEdAJkuHTsmVLxSo3sbIrgsdDDL/00047TdWtW1fjhUcNqdAmTZqkvv7664onyR5BQBCoFAEh6UqhqfjDO++8owYPHqwOPvjgMsKuU6eOOvHEE7WVTQbqvAmky8PqmmuuUfvvv38ZLs2bN9cWtHjP5K1HSH3DRkBI2ieiROHDYiTqWu3atcvICUubmBJMiJGoYMqUKSoL5E2OwOeff16RaRurmElWMxxk3jAIdMVKQIaMRAQBQSAcBISkw8FRW5MQFElOWYreoEGDcsSdFvJesmSJYgk2Y8Y9evTQY8nbbrttubrw9tC6dWud1gyPjKeffloxNCQiCAgC4SMgJB0+pmUlEpmN130mIvv06aNXzhGpz1ieZovlzao6/LVZwIHP8FVXXaUtcZayky6M5dEEjMKaxa947ty5OqAUaaHIA0nUP5IfMCa8cOFCxdAMOf2eeuopPRaMayGr+IgQSKIE8kWSOxKLv2PHjjoru/uNYLvtttMxUFj0c+edd+qFJZ999llZ/eSLICAIRI+AkHT0GFe4wurVq9XMmTPVmDFj9MINorlhmULWu+22mx5GqFmzZgUyN6QedLvFFlvoST0eGEyIMhF6+OGHq549eypCvpJde9myZRX0lh2CgCAQPwJC0vFjXvIVsY4hdMaDP/jgA+2yRhYShiOmTp2qSCM2fPhwdfPNN+sJzSFDhmirfeLEieqJJ57QZDtr1iw1f/58xTDGihUrZFiiZPTlQEHADgSEpO1oB9FCEBAEBIGCCAhJF4RFdgoCgoAgYAcCQtJ2tINoIQgIAoJAQQSEpAvCIjsFAUFAELADASFpO9pBtBAEBAFBoCACQtIFYZGdgoAgIAjYgYCQtB3tIFoIAoKAIFAQASHpgrDITkFAEBAE7EBASNqOdhAtBAFBQBAoiMD/AYfCZgU4r1OdAAAAAElFTkSuQmCC[/img][/td][/tr][/table][br]Select [b]all [/b]true equations.
Solve each equation.
[math]\frac{2}{5}=\frac{x}{15}[/math]
[math]\frac{4}{3}=\frac{x}{7}[/math]
[math]\frac{7}{5}=\frac{28}{x}[/math]
[math]\frac{11}{4}=\frac{5}{x}[/math]
[size=150]Select the shape that has 180 degree rotational symmetry.[/size]
[size=150]Name a quadrilateral in which the diagonal is also a line of symmetry. Explain how you know the diagonal is a line of symmetry. [/size]
In isosceles triangle [math]DAC[/math], [math]AD[/math] is congruent to [math]AC[/math] and [math]AB[/math] is an angle bisector of angle [math]DAC[/math]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALIAAAC6CAYAAAAK2RcFAAAXCklEQVR4Ae2dCfCV0//HJaLSvqi0at9U2pOyZE1CsrRMqDSaUpFlGooojChb2RJFhonQyAgVyhZFtIoWpUwREVly/vM6/9/J873f597vc597n/3zmblzv/e5z3OW93l9zz3r5xymxESBGChwWAzyIFkQBZSALBDEQgEBORbFKJkQkIWBWCggIMeiGCUTArIwEAsFBORYFKNkQkAWBkKnwKxZs9Rhhx2mpk6d6jhtArJjqeRGvxSoU6eOBnnChAmOoxSQHUslN/qhAPAC8qhRo1Tv3r0dRykgO5ZKbvRagb1796ry5csrmhYA3b17d8dRCsiOpZIbvVaAWpjaGKN9DNROTUB2qpTc56kCmzdv1u3iJUuW6Hh4p8Pn1Jzf6TREuU8UcKHAoEGDVN26ddXSpUv1a9q0aRrkVatWOQpNQHYkk9zkpQKm9qUGTn2ZGrqo+AXkohSS7z1XgE6dXccum7FkAdnzYpIIMilgamO7JgRwOx1LFpAzqSzfea4AoxS0j+0MkJ2OJQvIdgrKNV8UoDYGVkYs7IzxZIbknJiA7EQluSf0CgjIoS8iSaATBQRkJyrJPTkpsH79ejV79mz14Ycf5hROpocF5EzqyHc5KzB58uQCY8PpOna5RiQg56qgPJ9Wge+//74AxGay47XXXkv7jNsvBGS3yslztgrs3LlT3Xffferss89WJ554oi3ITseGbSNIc1FATiOMXC5agRUrVqibbrpJde7cWVWoUKEQtA0aNCh0jVp5/vz5RQee5R0CcpaCJfX2V199VQ0ePFg1b95clSpVqhCgZcqU0d/169dPPfHEE+qnn35SDz30UKH7Lr30Uk8kFJA9kTW6ge7fv189+uij6sILL9Rrg4888sgCMB5++OGqcuXKqmPHjmrEiBEqXXvXQAz8V1xxhV7ZtnjxYs+EEZA9kzb8ATMsNnHiRHXKKaeoKlWqKCA1HTLegbhmzZrqjDPOUOPHj1effPKJo0xZIeaBkiVLqpYtWzp61u1NArJb5SL23DvvvKNGjhypO2Bly5YtACzQ0lxo1KiRuvjii9WDDz6o6LS5sVSIf/zxRx3XkCFD3ATn+BkB2bFU0bjx77//Vs8++6yirdqwYUNdG1pr2WLFiuktRIwoANddd92lZsyYkZfMGYivuuqqQ+G98MILGmTa2F6agOyluh6HzTjtlClT9FBXjRo1dFPACu0RRxyhqlWrphfm3Hjjjer9998vlCI2fN5www2Frmd7wQ5iwuCfhTT99ttv2QaZ1f2+gYxgZhsL7+lWPGWV+pDePGbMGHXJJZfkNXW0Txnq6tSpk6pUqVKh9uzRRx+tjj/+eNWrVy917733qi1btjiOn/tpL7u1dBATXps2bfQ/mNuwnT7nG8iMHVprC/5mj5YXY4pOM+/VffTSGzdu7Dr4V1555dBQF8NaqbrRxqXzNHDgQDVnzhz166+/uo6LBxctWqSef/55V2FkgpgAy5Urp8vZVeBZPOQbyMbxhkkbOwJYNE0hxQ1mtrKTr3379pns2r7zc0v79IILLtC1KbWqFVpGERhNYMKBdbl02Lwwxnz5Ffnrr7+yCr4oiAmP/JA/r803kNOt9m/VqpVq3bq11/n0NXyzfcfaJuWn+/bbb9dDXXbt2RIlSqjatWurs846S02aNElt2LDB1zSziJ1/lE2bNul/rrlz52aMvyiIeZjwAHn69OkZw8rHl76BzE+MnVM6amoyGyejaUCeANOuPVu6dGnVpEkTxSzXzJkz1Z49ewLP/vLly9V5552nbr31VvXee+9lTI8TiAlg7NixWge3Q3kZE5HypS8EpTrfsKbBtJ2t16LyN0NdtFEvu+wy1axZM0V7luEtIDavihUrqnbt2qnhw4erhQsXZv3z7bUWQMZa4Ztvvll3Jl9//fWMUTqFmEC6du2qO6UZA8zTl76AbNyE2qU5KjXyjh079FDXueeeq+rVq6dS27MMddFkOO200/TO3x49eqj27dvbZTlU11j488Ybbyj+KflluPbaa9X27dtt05gNxARQtWpV3ca3DSzPF30BmY4KbWE7Y6G18fdl930Q1z7++GPFuGu3bt1U9erVFZCaGpZ3plzr16+v+vTpo9uTQJ5qTP0yxRs1o32Pl59UyxZinqezioZ+mC8g09Gz2w1rvC/afedH5omDpg2D9sx00QywrjegmUDbnn/Cq6++WtH2dTrUxUwW0H/xxRd+ZSVv8Tz11FPqpZdeOhSeG4jXrVun80+b2w/zBWQKlOZFqlEbA4ofkyMAyFBX3759dUfrmGOOKVDLFi9eXP8UUoOMGzdO8ZObizEhQb6feeaZXIIJ5Nk///xTT11TO7uBmEQz8kL+v/zyS1/y4DnIjBeTIasnGcBl0oDrXowhUxsw1MUuBSZdjjrqKB0X8fHiM9fPP/989cADD3j2j/T0008XyLcvJZqnSHbt2qXOPPNMrZd17YTT4M855xz9rNP7c73Pc5DN5ABLBc0LmPi5tsLtNiNvvfWWHsynh8y6gtT2LDVvixYt9D8OC1jCMNTlNq9+Pue2JjZppN+D9n6Z5yDz88TIhHkBthuAzVDXlVdeqefv2VpjHeqibcuC7y5duuhFMMuWLQvdUJdfhZprPLlCTPxM8KTr4OeaPrvnPQfZLtKirjH8Q8+ZUQHWLDCBYJoFvDMaUKtWLcVQWK4LXopKS9K+zwfEZvf0sGHDfJMvcJA/+ugjXVvTHmMmLLU9y4Lvpk2bqgEDBujJB7uhLt/UinlEBmK0zsXYKkWFU9TkSi5xpD6bM8iff/65nih48sknFfu9MtmCBQv0MBw//wyWM1JgalqaCTQXOnTooEaPHq3n6Z0OdWWKU75zpoCBmLUejIHnUmEw9U650hz0y3ICmXUCBkTemSTYtm2bXvVFj52RCdpJHGpibc8CMLNg7AVjmCaKY61+FZAf8RiIzegEay1YbL969WpX0bOOhDayn5YTyEzVWkHmb9qu1uYBU7nsBTMLZPwYM/ZTwKjHlQqxyc9XX32l11+wPsRqwM2vbyajTwMbfpprkFnDmgoxn+mcMYaLADLU5WdRZh9XOohNSJQx7V3G2rdu3aov40Xo008/NbcUemeNNRxcdNFFhb7z8oJrkElU27ZtC8F85513epleCTtPChQFsTWad999V11//fV6hIjNqpns5Zdf1kw8/vjjmW7L+3c5gczCaRbVWGtmtpP/+++/eU+oBJg/BbKB2MRKx7t///569Ih1JGzztzPWpMADtbmflhPIJPTgwYPq7bff1j83dBLIhMDsZxFmF5cbiIkB38b4u9i9e7eaN2+enk2lrbxy5UrNgEkFi6/ozPttOYOcmmC29wAzkxlSM6eqE+xntxCT6jvuuEOtXbv2UAbYj8eukocfflgPqdKW5heajbEMrfpteQeZDDA9bGCmxhYLXoFcICb1a9asSZsJOnifffaZMs5YWFPjt3kCMpn44IMPBGa/SzNNfLlCnCbYQpepoanAGLXy2zwDmYzQriJjDMX8888/fudN4lPK9XpiN+Kxq4bytjZB3ITj5hlPQSZBrKUQmN0UTe7P+FUTm5SyKYEZ3CDMc5DJFHvgBGZ/i9dviMkd68Hp7AVhvoBMxvBdBsw4kPZzMUkQogYdZxAQk2eG3YJytuMbyGSUfXACs7eYBwXxt99+q8sW/x1BmK8gk0GGaYAZf2DZ+hoLQqAoxcmYLtqaVWx+pv2ee+7Rcb/55pt+RnsoLt9BJmZmgwTmQ2WQlz+ChJgM9OzZU5dpXjLjIpBAQCadZne11MwuSi3lkaAhJjnsSsdxTVAWGMhkmN0l1My4l8WXglj2CoQBYlLNGnQcjQdlgYJMptkdIjC7K/6wQGwOvMH5TVAWOMhknF0HwIzDlAMHDgSlRaTiDQvEiIaLLcqPrW9BWShAJvO4VhKYnWFgIMbHRxjs8ssv12Xn9YE3mfIaGpBJJPvEBOZMxaX0skk0CgvEpBZ3DUF7Hg0VyFaYOZ3ojz/+yFyqCfs2bDWxkR/XWOwUCtJCBzJimJpZYP4PjbBCbA68wcF5kBZKkK0wc65F0mvmsEJMOeFNiKZO0JuOQwtyKsy///57kP/wgcUdZogR5ZprrtEgb9y4MTCNiDjUIJNA08ygZk4azGGHmPLhoB88oQZtoQfZCjPz+UX5lwta0HzFHwWIySvHVfAK2iIBMiKZmjkJMEcFYsqFHSG4AAjaIgOyFWb8Ise1Zo4SxGZJ7ogRI4LmOPxt5FSFTM0MzEHOJKWmKx+fowQx+b3lllt0Rw8HPUFbpGpkI1YcYY4axJQF/isYeguDhSMVLpQwMHN6UNQdgkcRYoqM2Tw/D7zJhElkQSZTcYA5qhCjPydo4fs6DBZpkK0wc6Ze1GrmKENsDrzBgXsYLPIgp8K8b9++MOhaZBqiDDGZ49Qt2sccsREGiwXICGmaGdTMYYc56hCjNwu6ADksPkpiA7IVZk4m+uWXX8JQURRKQxwgJlOcEcI+vbBYrEBGVFMzhxHmuECMzhxyxLmIYbHYgRxWmOMEMZ1qmhU9evQIC8fRm9lzqpypmTlR9eeff3b6mCf3xQliBHruuec0yJMnT/ZELzeBxrJGNkKEAea4QYy2AwcO1CDj7y0sFmuQEdnAzCmre/fu9VX3OECMe4bFixcXOKWpefPmejLEVzGLiCz2IAcFcxwgRjvjqJ02MZ6EOH2A0Ypy5cqpLVu2FIGXf18nAmS/YY4LxOhGx46TusjT0KFDVfv27XWzArB5ValSRXf6xo4d6x+1NjElBmQrzPS2vTrQME4Q2/Ciz1QE4H79+qnZs2er6667Tp1++umKxVtBWqJA9hrmuEOMfqNGjdI18dKlS4PktlDciQPZCjM1SbqjaAspVcSFJECMBB06dAjswJtMRZBIkBHEjGbkA+akQIxulSpV0h29TFAF8V1iQc4XzEmCGM3Y+t+iRYsgWM0YZ6JBtsKMy6c9e/ZkFCv1y6RBbH7F8L4ZNks8yBSIKaBsYE4axOjE0byMWMyZMydsHMd3rUW2Slth3r17d8bHH3nkEV2gYXLtmjHBefqS/gQgh9HCmaqAlDIwn3rqqSodzEmFmCKpUaOGKlWqVEClkzlaATlFHzuYzUE9SYYYmdhsGuSBNylFVeCjgFxAjv//YGBu2LChqlmzpv45bdasWSKbE0YeOsI0K3CME0YTkNOUymOPPaYLjsIzL9YVJNWmT5+udeCE0zCagJymVEaPHn0IYAMy719//XWaJ+J9mVVv5H/btm2hzKiAnKZYxo8fbwvyzp070zwR78v169dXJUqUCG0mBeQ0RbN+/Xq97tZaGx977LHqhx9+SPNEvC+z2ZRRi7CagJyhZFasWKEGDx6s19uOGTNGFS9eXHXr1k3t2rUrw1Px+8oceEPew2oCchYlw2gGQ1BJg3nevHm6mcU/c1hNQM6yZICZwxGTBDO/SjSx2CkSVkscyGxAZVG4eW3evDnrsgFmOj4nn3yySkLnr2XLlrpZlbVQPj6QOJCnTp1aaDSifPnyatasWVnJDsxswkwCzGXKlNHrkLMSyOebEwfyoEGDVPfu3Q/JTA3NNWDO1oC5ZMmSGmbcrMbVaFaE4cCbTPomDuRWrVqpCRMmFNBkyZIlupbmPVsDZhbSdO3aVcUR5mXLlmltwr7SL1EgU/tSu8yfP78Ar4CNnwa3BsylS5eOJcxs80ezuXPnupXHl+cSBbKpeXFObTp7t912m4Y42zZyaukAM+dpnHTSSWrHjh2pX0f2c+fOnfVm04MHD4Y6D4kCmZqX2sX6om3spklhV6rATMcoTjBXrlxZ58kuv2G6liiQe/furXgZs3b0+DsfBsxly5bVMG/fvj0fQQYaBptNmzRpEmganESeKJDr1KlTqKNn2s0My+XLgJk2d5cuXVSUYf7mm2/0r1efPn3yJY1n4SQGZCY+aFKkNiPM9dQOYK6KA3OFChUiDfPdd9+tNZsyZUqucnj+fGJABlRATm1CMIZM7elmhq+o0gHmihUrKjpM3333XVG3h+57jq9Asyh0XhMDsunoceysedWtW1fR3Fi1apVnEAEz3nmiCPNxxx2nzwrxTJw8BpwYkBleA2brK7WZkUddCwQFzPT+gTmsOywKJPh/H1gcxT96FCwxIAddGMDMnr9OnTpFAmZz4A2e/qNgArKPpQTMVatWjQTMM2fO1O3jcePG+aiQ+6gEZPfauXoSmKtVq6Zh3rp1q6sw/HiIM6bp6C1fvtyP6HKOQ0DOWcLsAwDm6tWrq44dO6qwwoxPD3bDRMUE5IBKCpjZzAnMYTpUxsjB8lQ220bFBOQASwqYGeLCC3zYYKZZwShLVExADrikgBm3XGGCecGCBbp9PHz48IDVcR69gOxcK8/uBOZatWppmL2YYcw24cOGDdMgv/jii9k+Gtj9AnJg0heMGJiZfOAcu6Bhbt26tT5iAX8WUTEBOUQlBcxMmwNzkOc8swzVzR7GIKUUkINU3yZuYK5Xr55q165dYDDT0TvhhBNsUhfeSwJyCMsGmHGoHQTMuAkD5P79+4dQmfRJEpDTaxPoN8CMB0xgZoG7X8aUNCDPmDHDryjzEo+AnBcZvQkEmBs0aKDatm3rG8w4nAHkqLk2EJC9YTBvoQIz08XAvGnTpryFmy4gVujh2iBqJiBHoMSAuXHjxr7AzGZTfgWiZgJyREoMmNnNjOsqr2pmtjTRrOjVq1dEVPkvmQLyf1qE/i9gbtq0qYbZi7NM7r//fg3ypEmTQq9FagIF5FRFQv4ZmDkqrU2bNnk/mKdnz54aZIbgomYCctRK7H9nZzdv3lzDvHHjxrzloHbt2hkPvGEHOu7GcDPGa9q0aYFPp5vMC8hGiYi9UzPnG2Y2m7Ks1M7YvMu0Na4TcMuLGwU8m1pd9No959c1AdkvpT2Ix8DMIp9ca2Zz4A2uElLN+AQZNWpUIb8gqX5CUp/167OA7JfSHsVjhXnDhg2uY5kzZ45uH+NG1mqASk0MxGE2ATnMpeMwbQZmfurdwjxgwAAN8sKFCwvECsA0J8JS8xZInOWDgGwRI8p/5gozY9ScI3jgwIECMrBGmvZw2E1ADnsJZZE+K8yc3JqNcXwE3pBSjQmSXJ2gp4bpxWcB2QtVAwzTwMx64mxgBlhW2lkNn3hc98u1mDXubP8WkLNVLAL3W2Fet25dkSletGiRBnbIkCEF7vXK5W6BSPL0QUDOk5BhCyYbmEeOHKlBnj17dqFsUCNLG7mQLHLBTwUMzJxcmqlmpklRrFgx21NcjTveVEfoQW+QTdVRauRURWL22Qrz2rVrbXPHODEbTu2MYTfOXaFm5j4mTHgPy4yeSbOAbJSI8buBuUWLFsoOZiBlIVImo+NnfEzT+QvbuLKAnKn0YvSdFeY1a9Ycytnq1at1bdu3b99D16L4h4AcxVJzmWY7mCdOnKhBzuepVi6Tl9NjAnJO8kXvYQMzK+emT5+u/TQzo+flOSp+qCQg+6FyyOIAZjaZ0jY2L/bp7dmzJ2QpdZ4cAdm5VrG5c//+/dq3m4HYvEdxi5MpFAHZKJGgd1bIGXit70OHDo2sCgJyZIsut4Q3atSoEMysSY6qCchRLbkc0836Cjx/mho5Sk697bIuINupkqBrK1eujJx7LLviEZDtVJFrkVNAQI5ckUmC7RQQkO1UkWuRU0BAjlyRSYLtFBCQ7VSRa5FTQECOXJFJgu0UEJDtVJFrkVNAQI5ckUmC7RQQkO1UkWuRU0BAjlyRSYLtFBCQ7VSRa5FTQECOXJFJgu0UEJDtVJFrkVNAQI5ckUmC7RQQkO1UkWuRU0BAjlyRSYLtFBCQ7VSRa5FTQECOXJFJgu0UEJDtVJFrkVNAQI5ckUmC7RT4Py6gKpO/KjVCAAAAAElFTkSuQmCC[/img][br]How does Kiran know that [math]AB[/math] is a perpendicular bisector of segment [math]CD[/math]?
In the figure shown, lines [math]f[/math] and [math]g[/math] are parallel. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUgAAAE4CAYAAAA5NmryAAAgAElEQVR4Ae2dCbwN5f/Hf0KWRMle9i0UQshStEpIkiRrkpAQSkLWECqlUhHJkqRClij7LumGsictWiRCKHz/r8/z/839zb33nHvOmeXMM3M+z+t1X3fOnJlneT9z3/eZmWf5jzCQAAmQAAmEJPCfkHu5kwRIgARIQChIXgQkQAIkEIYABRkGDHeTAAmQAAXJa4AESIAEwhCgIMOA4W4SIAESoCB5DZAACZBAGAIUZBgw3E0CJEACFCSvARIgARIIQ4CCDAOGu0mABEiAguQ1QAIkEGgCSUlJlstHQVpGxxNJgAR0J9C+fXspWbKkHDhwwFJWKUhL2HgSCZCA7gTuvfde+c9//iNTpkyxnFUK0jI6nkgCJKAjgZMnT8odd9yh5DhnzhxbWaQgbeHjySRAAjoROHz4sNSqVUuyZ88uS5YssZ01CtI2QkZAAiSgA4G9e/fKtddeK/nz55d169Y5kiUK0hGMjIQESMBLAl9++aUUL15cSpUqJV9//bVjWaEgHUPJiEiABLwgsGrVKsmTJ49UrlzZ8tvqcPmmIMOR4X4SIAHtCSxcuFCyZMkidevWld9//93x/FKQjiNlhCRAAvEg8N5776k31Q0bNpQzZ864kiQF6QpWRkoCJOAmgbfeekvJsUWLFm4mwyUXXKXLyEmABBwn8OKLLyo5duzY0fG4U0fIFmRqIvxMAiSgLYGhQ4cqOfbs2TMueaQg44KZiZAACdgl0LdvXyXHgQMH2o0q6vMpyKhR8UASIAGvCHTp0kXJcfTo0XHNAgUZV9xMjARIIFYCrVu3VnJ87bXXYj3V9vEUpG2EjIAESMANAufPn5e7775byfHdd991I4mIcVKQERHxABIggXgTOHbsmNxyyy2SIUMG+eijj+KdfHJ6FGQyCm6QAAnoQOCHH36Q6tWrS86cOeWzzz7zNEsUpKf4mTgJkICZwLfffivlypWTK6+8UjZt2mT+ypNtCtIT7EyUBEggNYHNmzdL4cKFpWzZsvLNN9+k/tqTzxSkJ9iZKAmQgJnA559/LpdddplUq1ZNDh06ZP7K020K0lP8TJwESGDevHmSMWNGqV+/vvz5559aAbEtyG3btgmG/dSrV0/9Hjx4sODnu+++06qgzAwJkIB+BKZPn6668TRp0kTOnTunXQZtCXLFihWqcBg8ju1KlSpJ0aJF1Wt53f4TaEeeGSKBBCfw+uuvK3+0atVKWxK2BHnTTTfJs88+m1w4bEOSDCRAAiSQHoExY8YoOXbu3Dm9wzz/zpYgseYsWo5G6NGjh0CaDCRAAiQQjsCgQYOUHPv06RPuEG322xIkbqeNaYcgSryF8rLXuzZUmRESIIGQBHr16qXkOGTIkJDf67bTliAhQ7Qi8YOWI+WoW/UyPySgD4FOnTopV4wbN06fTEXIiWVB4i01WpB8Wx2BML8mARKQli1bKjm++eabvqJhWZBoLeKWGrfYL730kqxcudJXBWdmSYAE3Cdw9uxZueuuu5QcZ82a5X6CDqdgSZDowoO+jritNn5wm411adm9x+EaYnQk4FMCR44cUX7InDmzLFiwwJelsCRIdOVB30dzgBghySlTpph3c5sESCABCRw8eFCqVKkiuXPn9vXdZcyCxDNHiDD1s0dDkOZuPwl4XbDIJJDwBLZv3y6lS5dW7yi2bt3qax4xCxKlzZUrlzRt2lT9Z8Czx6lTp6rba/aB9PW1wMyTgG0C69evl4IFC0qFChVkz549tuPzOgJLgkTrsV27dsnPHyFG3lp7XZVMnwS8JbB06VLJkSOH1KxZU37++WdvM+NQ6pYE6VDajIYESCAgBObOnasevd12221y4sSJgJRKhIIMTFWyICTgDQE8YsN7iWbNmnmTARdTpSBdhMuoSSDoBCZMmKDk2LZt20AWlYIMZLWyUCTgPoGRI0cqOXbr1s39xDxKgYL0CDyTJQE/E+jfv7+SY79+/fxcjIh5T1eQ+/fvl8cee8zzpRcjloIHkAAJxI3A448/ruQ4fPjwuKXpVULpCnLs2LFy1VVXKRhYhhFNaa/XqfUKFNMlARIQ6dChg/LB+PHjEwJHuoI0CGDFse7duyfLslChQkqWy5YtMw7hbxIggYATaN68uZLj22+/HfCS/q94UQnyf4eLLF++XMkS69fi1T5laabDbRIIHoFTp05JgwYN1N/7nDlzglfAdEoUsyDNcUGWeB5hlmXXrl2FLUszJW6TgH8J/PLLL1K7dm3Jli2bLF682L8FsZhzW4I0p4lJKiDLIkWKqP80GI8JWWL4EQMJkID/COzbt08qVqwo+fLlk7Vr1/qvAA7k2DFBmvMSSpZdunShLM2QuE0CGhPAevfFixeXkiVLSlJSksY5dTdrrgjSnGXIEqsdmluWkOWnn35qPozbJEACmhBYvXq15M2bVy3hfODAAU1y5U02XBekuViYGg2yxFo2eMFToEABoSzNhLhNAt4SWLRokWTNmlXq1Kkjv/32m7eZ0SD1uArSXF7IEuvZmGX56KOPsmVphsRtEogjgdmzZ6uGy5133imnT5+OY8r6JuWZIM1IUssyf/78AlkuWbLEfBi3SYAEXCIwadIkJccWLVq4lII/o9VCkGZ0q1atUi3LYsWKqQqjLM10uE0CzhPAqqR45PXQQw85H7nPY9ROkGaekGWvXr3ELMvOnTuzZWmGxG0SsEFg2LBhSo54N8CQloDWgjRnF2/WIEt0PcB/O/TNgiwTsfOqmQu3ScAqgSeffFL9LQ0YMMBqFIE/zzeCNNdEKFk+8sgjlKUZErdJIB0CGMSBhsaoUaPSOYpf+VKQ5mqDLJ944okULUvK0kyI2ySQkkCbNm2UHF999dWUX/BTGgK+F6S5RGvWrFGyLFGihLoA0NkVskTfLgYSSHQCFy5cUMs1o+U4bdq0RMcRVfkDJUhziUPJslOnTpSlGRK3E4bA8ePH5dZbb1UNh48++ihhym23oIEVpBkMZNm7d28xtywhy4ULF5oP4zYJBJLAjz/+KDVq1JBLL72UM23FWMMJIUgzE8xKAlliED5uNfLkySOUpZkQt4NEYNeuXVK+fHk1b+vGjRuDVLS4lCXhBGmmCln26dMnhSwffvhhtizNkLjtWwJbtmxRk8SULVtWdu7c6dtyeJnxhBakGXxqWV5xxRUCWX7yySfmw7hNAr4ggMmsL7/8cqlataocOnTIF3nWMZMUZIhaWbdunWpZlipVSt2GU5YhIHGXtgTmz58vmTJlknr16snRo0e1zacfMkZBRqglyLJv375ilmXHjh3ZsozAjV97Q2DGjBnqn3rjxo3l33//9SYTAUqVgoyhMtevX69kWbp0aXUR5s6dWyDLBQsWxBALDyUBdwhMnDhRXZetWrVyJ4EEjJWCtFjpoWSJ2VAoS4tAeZotAljDHr0yMDCCwTkCFKQDLCFLDPw3tywhSzwLYiABtwk8++yzSo7ovsbgLAEK0lmesmHDBiXLMmXKqIsWbxIpS4chM7pkApiHAC3HwYMHJ+/jhnMEKEjnWKaJCbJ86qmnxCzLDh06sGWZhhR3WCGA22nIEbfXDO4QoCDd4Zom1tSyvOyyywSynDdvXppjuYMEIhF44IEHlBzfeOONSIfyexsEKEgb8KyeiiFfaFlihANaAJSlVZKJd94///wjjRo1UtfNzJkzEw9AnEtMQcYZeOrkIMt+/fqlkGX79u3ZskwNip/ljz/+UJ2/0QmcvSXic0FQkPHhHFUqmzZtUrK8+uqrVQshV65cAll+/PHHUZ3Pg4JL4ODBg2rYIF76rVixIrgF1axkFKRmFWJkJ5Qs27VrR1kagBLo944dO9SLviJFisgXX3yRQCX3vqgUpPd1EDEHkOXTTz8t5pYlZRkRWyAOwMu9QoUKSYUKFWT37t2BKJOfCkFB+qm2RGTz5s1KluXKlVO34Tlz5hTIkrNE+6wio8ju0qVL1SS3mOz2p59+iuIMHuI0AQrSaaJxjA+y7N+/v5hl2bZtW8oyjnXgVlIffvih+geIZRL++usvt5JhvBEIUJARAPnl63CyxB8ag78IvPPOO0qO99xzj78yHsDcUpABrFTMJI2WJabaRz9LrEWCliVlqX9lT5gwQdUZ6ovBewIUpPd14GoOIMtnnnkmhSyxLjJkiWVAGfQhMGrUKCXHrl276pOpBM8JBZlAFwC6iJhlmSNHDoEs586dS1l6fB2gXtDaxwgrBn0IUJD61EVcc2LIEt1H8IdpluX58+fjmpdET+zxxx9XdTB8+PBER6Fd+SlI7aok/hmCLAcMGKD62hmybN26tWpZUpbu1gemwgPzl156yd2EGLslAhSkJWzBPWnr1q1Kltdcc436w73kkksEsvzggw+EsnS23u+77z7FePLkyc5GzNgcI0BBOoYyeBGFkuWDDz6oZHnu3LngFThOJfr777+lQYMGSo7vv/9+nFJlMlYIUJBWqCXgOV9++aUMHDhQzC3LRJDld999JytXrnSsxn/99VepU6eOZM2aVRYvXuxYvIzIHQIUpDtcAx2rIctrr71WtYKyZ88ukOWcOXMkSC1LDN/EXJ14RuhE2L9/v1SqVEny5s0ra9ascSJKxuEyAWdq3uVMMnp9CUCWgwYNErMssewoZOnndZmxEBammzMWxLJbA1999ZWUKFFC/WCbwR8EKEh/1JMvcrlt27YUssyWLZtAlnjO5idZ/vnnn2oCEJQHcy/abUGitZgvXz7VekQrksE/BChI/9SVr3JqyLJixYpKMH6VpV1B4jkjyl67dm3B80cGfxGgIP1VX77MLWSJW1WzLLHoFFqWWGNF52BHkCgfWp94Y4031wz+I0BB+q/OfJ1jPH+DLPGyAvLA21zIcvbs2VrK0qog0bcR5UNfRwb/EqAg/Vt3vs95KFm2bNlSyfLs2bNalM+KIMePH6/kiGV9GfxNgIL0d/0FJvdJSUkyePDgFC1LHWQZqyAxnhotR4yvZvA/AQrS/3UYuBIYsqxcubKSTZYsWQSyfO+99yTeLctYBImZeCBHzMyTXsBbcoy9xoqV+Jk6dWp6h/M7DwlQkB7CZ9KRCUCWQ4YMEbMs77//fiXLM2fORI7A5hHRCrJbt25KjpjTMb2A+ND5/O6771bPYo3+lk2bNk3vNH7nEQEK0iPwTDZ2Al9//XVIWc6aNUvckmU0gsTs32g5YjbwSAGtR8RpDnjLj/NT7zcfw21vCFCQ3nBnqjYJGLK87rrrlFwuvvhiQcvSaVmGEpo561g3BnLDOjJ2AgVph55751KQ7rFlzHEiAFkOHTpUzLJs0aKFkuXp06ddyQVWGsSKgxCb3bV+jBYkJsZg0IsABalXfTA3Ngls3749hSwzZ84skOXMmTPFKVlijeqaNWuqWdiXLVtmM8einkfedNNNtuNhBM4ToCCdZ8oYNSFgyLJKlSqqpeeELHfv3q1mXi9YsKBs2LDBdklffPFFNSkGbuUZ9CNAQepXJ8yRCwR27Nghw4YNE7MsMcoFLctohwFiaYoiRYpImTJlBPHZDVOmTFFyxC02g54EKEg964W5cpGAIcuqVauqlmWmTJnUkMAZM2aElSXeMOfOnVsJ9vvvv7edO8rRNsK4REBBxgUzE9GVAGSJ0S9mWTZv3lwgy1OnTqlsL1iwQHB7jueEf/zxh+2iUI62EcYtAgoybqiZkO4Edu7cmUaWNWrUUK3MO++805HJNCBHvPnGSBos5WD+4a22flcIBalfnTBHGhCALDHaBTLDT8aMGQUty+nTpye3LK1kE61QI87Uv/km2wpRd8+hIN3ly9hdJIDnghiiZ6wbU69ePcfGNY8bN06JrFOnTgJZjhgxQqpVq5Ysy3vvvVfJ8uTJky6WkFF7TYCC9LoGmL5lAkWLFpUePXqoIXqQpXH7iq4zdgJmFULr7oknnkgTzTfffJNClhdddJFAlu+++65Qlmlw+X4HBen7KmQBzAQgTDu3qr1791ZyxCQSkYIhy+uvv16dQ1lGIua/7ylI/9UZc5wOgXbt2lkWZOfOnZXoxo4dm04Kob/69ttv5bnnnhOzLJs1a6ZalidOnAh9EvdqT4CC1L6KmMFoCWAda9wa43esAasv4tyJEyfGemqa4w1ZVq9eXcWZIUMGgSynTZsmlGUaXFrvoCC1rh5mLhIBPHfEyxnIrVixYjHLEcvRNm7cWJ2Pvo9OB8hy5MiRYpYlZgCCLDHhBYPeBChIveuHuYtAADPgGC9ocHsNUUKa0YSjR48quaILz/z586M5xdYxu3btoixtEYz/yRRk/JkzRRcJ4A02JBkpYLgguu2gi9Dy5csjHe7494YsjY7oyDNalphXki1Lx3FbjjDylWQ5ap5IAvEngNYkZJPeqBT0ayxbtqwULlxYtmzZEv9MpkoRssRSDWZZon8nZHn8+PFUR/NjPAlQkPGkzbRcJxCpBblx40YpVKiQlC9fXiCmaANu26O9dY82zlDHYTo1yjIUGW/2UZDecGeqNgmgpYiFvNCpG+OZsTIgVghM7xkkJrfNmTOnemGCSW+jDXgrnitXLsvdh6JNJ/VxhiwxOS/KhR+0LFFWtixT03LnMwXpDlfG6jIBTDCL1iI6hRs/6CQebtkCSA7dbW655ZaY5IJ08JzSSMPlYoWNfs+ePTJ69Gg1k7khS4wVhyyPHTsW9jx+YY8ABWmPH8/2AQF0qTFaXxcuXIgpx5AQxIuRNXZG6MSUaISDw8kSjwAoywjwYvyagowRGA/3F4FXX31VybFNmzYxZxwt1EqVKglakToJ0lwQyPL555+XG264Ifk2HFKnLM2UrG87Jkg8E8LzoPTeHlrPJs8kgdgJ4JYULccuXbrEfDJu1XFrbVzPugrSXLC9e/emkWWTJk2ULLnmjZlU9NuOCBIddDGzCm5BohnkH332eCQJWCMwYMAAJccnn3zSUgRoOaIFaQQ/CNLIK34bsqxVq1ZyyxKyfPvtt1WL2Hwst8MTsC1I/IfFf+lwD8fDJ81vSMAdAnhmiGsSi3RZCaFkGGqflbi9OAeyHDNmjJhlieGVkCVGEzGEJ2BbkLhw8N+WgQR0INCxY0clRyxpYDVAruhChDHexg/GeeOWG5/j0R/Sat4jnbdv3z7KMhIk0/eWBYlnGj179lQXjXHhWJlFxZQXbpKALQItWrRQcpw0aZKtePA8PfUPHiOhIYD9QblbMmRZu3ZtxQ3/GNCynDx5MluW/72CLAsSFwkuFkBFKxLbfBBs6++SJ1skcPr0acGiWrgWZ8+ebTGW9E/z8y12+iX7/2/3798vmAfTLMtGjRopWTqxkmM0edDxGMuCRGGM54/Gmz4dC8g8BZvAb7/9JnXr1pUsWbLIokWLXCts0AVpBhdOlmiZJ5osbQkSz2IwBIuBBLwggD9kPCvMkyePrF692ossBD5NMMYCZnXq1Em+DUfLMlFkaUuQdtf/CPzVxQK6RiApKUlKliwpxYsXT+6r6FpijFgROHDgQBpZ3nXXXUqWR44cCSQlW4Jkv8dAXhPaF2rt2rWSL18+qVixouBFA0P8CRiyxOMNPPvFD2T51ltvSZBkaUuQgMI31/G/OBM5xcWLF0v27NlVn75ff/01kVFoU3bI8oUXXlDPgg1ZNmzYMBCytCxI4w0231xrc50GPiNz5sxRLZU77rhDTp06Ffjy+rGA6N0STpa///6774pkWZAYhoXhhQwkEA8CGPWB1knz5s3jkRzTcICAIcsbb7wx+TYcLcs333xT/CJLy4JEx1nMGsJAAm4TGD9+vPoD69Chg9tJMX6XCBw8eFCNbTfLEn1XIUt01dI1WBYkWo9+HnKla4UwXykJjBgxQsmxe/fuKb/gJ98S8JMsYxYkOsxi2nf0f+TzR99eo77IeL9+/ZQc+/fv74v8MpOxE4AsMW4ePWKMFzxoWb7xxhtatCxjFiRurdOb2j52RDyDBNIS6Natm/qDGTlyZNovuSeQBLAUb2pZNmjQQMnSqx4LMQsykDXDQmlFAP+E0ZqYMGGCVvliZuJHwJAlZk8yWpaQ5cSJEyWesqQg41fnTCkKAs2aNVN/EFiMioEEQACyxIs6L2RJQfIa1ILAiRMn5LbbblNynDt3rhZ5Yib0I3Do0KE0skS/WLQsf/nlF8czTEE6jpQRxkrg559/VotOXXLJJbJ06dJYT+fxCUrAkGX9+vWTb8Mhy9dff90xWVKQCXpx6VJsrMp3zTXXSIECBWT9+vW6ZIv58BmBH374QV5++WUxy/L2229Xsjx8+LDl0qQrSMzzePPNN8srr7wiyAADCThJYOvWrWo0VunSpWX79u1ORs24EpiAIUu4Cy94MFWb1ZCuIF977TWBhY23SEgQlqYsreLmeQaBlStXSu7cuaVKlSqCvnAMJOAGAbgKw1SthnQFaUSKJiru682yRFMWssRzAAYSiIXAJ598IhdffLFg2FmizVAdCyce6z2BqARpzmY4WeI1PGVpJsXtUARmzZql7kgwd+DZs2dDHcJ9JKANgZgFac45XqujZYk3R8ZtOFqWkCX6LjGQgJkAJibAddKyZUvzbm6TgLYEbAnSXCrIEn2RzLJEx07K0kwpcbcxRyDk2KlTp8SFwJL7joBjgjSXHEOBIEsMDTJalpAlxlmyZWkmlRjbQ4YMUddBr169EqPALGVgCLgiSDOdULLEzB2QJd9emkkFc7tPnz5KjoMGDQpmAVmqQBNwXZBmepAlpjEytywpSzOhYG137txZyXHMmDHBKhhLkzAE4ipIM1XMIgxZYu434zYcssRSDmxZmkn5c/vBBx9U9YqXeAwk4FcCngnSDCyULNFHDrLEuhYM/iFw7tw5adKkiZLj9OnT/ZNx5pQEQhDQQpDmfEGW6A5ibllClngLSlmaSem3jRnm0c0rY8aMMm/ePP0yyByRQIwEtBOkOf9Y+QyyxEpoxm04ZWkmpM82Bglcf/31aimO5cuX65Mx5oQEbBDQWpDmckGWb731VgpZ1q1bV7UssXA5g3cEvvnmG7n66qvlqquuks2bN3uXEaZMAg4T8I0gzeU+cuRISFmOGzdOKEszKfe3N23aJFdeeaWUK1dOvv32W/cTZAokEEcCvhSkmY8hS4ztNW7D0bKELPfv328+lNsOE/jss88kZ86cUr16dfnxxx8djp3RkYD3BHwvSDNCyHLSpEliliXmgks0WWK98sGDB6f5MbOyu/3xxx/LRRddpOYLPX78uN3oeD4JaEkgUII0E8Y0WpBlo0aNkluWkOXYsWMD37JEf9KiRYuqtYaxbfyY+djZfvfddxXTu+++W86fP28nKp5LAloTCKwgzdRDybJ27dpKlvv27TMfGohto8O9G4XBJMp4lNG6dWs3omecJKAVgYQQpJk4ZDl58uQULcugyTJXrlyyYsUKc7Ed2X7++eeVHLt06eJIfIyEBHQnkHCCNFfI0aNHlSwbN26cfBsOWWLssJ9blmjhOS3IgQMHKkZ9+/Y1I+Q2CQSaQEIL0lyzkCXWrjDLslatWkqWe/fuNR+q/bbxNt/4XaxYMfnoo48s57tnz55KjkOHDrUcB08kAT8SoCBD1BqGzIWSJW4x/SBLDMk0hmXi97PPPqsEZ0WSHTt2VOdiXDwDCSQaAQoyQo0bsjQmYECrDC1Lv8jSKF67du3U22zjczS/77//fiVHjGBiIIFEJEBBxlDrkCX6GJplecMNNyhZ7tmzJ4aY4n8oWpF4ux1NOHPmTPKQzvfeey+aU3gMCQSSAAVpsVqPHTumZIm+gMazPshy9OjRoqMsIUe0IiMFjHnHSKQsWbLIwoUL0z1827ZtgvWtjdv5dA/mlyTgQwIUpAOVFkqWNWvWVLLcvXu3AylEHwWkheUs8BsBb7ObNm2qZtmJJDKMY7/uuuvkiiuukNWrV4dNFK3Ryy67TP1jqFSpUtQt07AR8gsS0JQABelwxUCWU6dOFXPLMp6yhATRWjRategTibwYwgxX3K+//lpKlSoleOP95ZdfhjtMvfBBnFZe+ISNlF+QgKYEKEgXKwZjlCFLtOAMYUGWo0aNkni3LNMr5rp16yR//vxy7bXXpvuWHvJFOZzuY5le3vgdCXhJgIKME33I8p133kkhyxo1aihZ7tq1K065SJvMkiVLJHv27OrNPNY2Ty+gqw9uqRlIIFEIUJAe1PRff/0VUpYjR46UeMrygw8+UC3C22+/XU6ePBmRBG7V8aLHeK6Jtc7RiRxv9xlIIIgEKEiPa9WQ5T333JN8G46WpduyRHcl3C7fe++9URPAs83KlSurZ5x4BokfSBMvbCjJqDHyQB8RoCA1qizIctq0aQJZZsiQQQkMk9FClk7O1v3yyy+ruNu3bx9T6SFI/KQOmFqNI21SU+HnIBCgIDWtxRMnToSU5XPPPWdLljgfLcfHHnss5pJDjujikzpgfzR9LFOfx88koDsBClL3GhIRQ5bNmjVL0bKE7LBgVrTh6aefVnLEbysBcsQtdeoQTpypj+NnEvAbAQrSZzUGWWJGb8gSSx6gNYjlViPJEi1GHIvjrIZQ3XzQvxLxsuuPVao8T2cCFKTOtRMhb3jzDFniRYtZliNGjEjRssTtLyT2yiuvRIgx8tfGyx307cQPXtD06NEj8ok8ggR8SICC9KDS0BLDGOZwP1ayFEqW1apVkwoVKig5QmxOBeQft9t4MRNphI5TaTIeEvCCAAXpAXXIBS26cD92s3Tq1Ck1UzpGxxhpQJZoWe7cudNu9DyfBBKGAAWpUVXjVjVUN5pYs3j48GHBzEKXXHKJzJ8/X6ZPny7NmzeXjBkzKmFClsOHD6csYwXL4xOOAAWpSZWjozWe59mdBAJTrWFMNVqP69evT1E6tCxnzJihZJkpUyYly6pVqypZ7tixI8Wx/EACJCBCQWpyFeC2Gx2u7QTMwoPZeDArD2bnSS/8/fffIWU5bNgwoSzTI8fvEokABalBbRutRzsvUlatWqXmcfJENscAAA6kSURBVMR8jniJEkswZHnfffeJuWVJWcZCkccGkQAFqUGtQoyYY9Fq+OSTT+Tiiy9WM4EfOXLEajTqPMhy5syZAllmzpxZ3YZXqVJFIMvt27fbipsnk4DfCFCQGtQYbq1xi20lYM0YvKlu2LChYC0ZJ8Pp06eVLFu0aJFCllj+lbJ0kjTj0pUABelxzRgdr63MhoPVBiFHrD7odgglS9zOQ5aRnne6nTfGTwJuEaAg3SIbZbyYgNbKRA8vvPCCkuPDDz8cMiUM/cNcjZizEbP2ODkUEC3VWbNmCVqWuLWHpCnLkNXAnT4nQEF6WIGQFuQS60sVtNpwHgQYKhitUvSrRBr4jWecdl4ChUoH+wxZohVrluWQIUPYsgwHjft9Q4CC9LCq0Ck81Ow46WWpb9++So4DBw4MexjiTT0+Gp8x2a2bAbLEM1GzLJEmZJmUlORm0oybBFwhQEG6gjW6SNG6i6X1+Oijjyo5Pv/88+kmEEqQeAkUz/Vkzp49myxLrLGNFi9kOXjwYMoy3drjlzoRoCB1qo108vLggw8qybz++uvpHPX/X2E0Dm6pjeeOmFDCiVE6ERMOc4Ahy5YtWwplGQYSd2tJgILUslr+l6nz58+r23C0wDC1WbQBM+1Akmi14bfdIYzRphvpOMhy9uzZAllmzZpVSR8tW7Qsv/rqq0in83sSiCsBCjKuuGNL7NixY3LzzTeruR4//vjjqE9GlyG8vTZutSFIfLbSlSjqRC0c+M8//4SUJR4HUJYWgPIUxwlQkI4jdSbCH374Qc0UnjNnTvn8889jijR11yGIES+D3H5JE1MmUx1syPKBBx5I0bKkLFOB4se4EqAg44o7usSwgmG5cuXkyiuvlM2bN0d30n+PMpZASP3yB5LEbbrxXDKmSON88L///ivvv/++QJbZsmVT+a5YsaIabcQJeuNcGQmeHAWp2QUAIV511VVy9dVXp1g2IdpsQowQYWpBGvv9JhhDlq1atUohy0GDBnE282gvCh5nmQAFaRmd8yfiVhrPC7EIF26xrQbcYuN2Gks6IKDViM94JunnAFnOmTNHzLLE3JeQJaZ6YyABpwlQkE4TtRjfvHnz1MuY+vXrC17O2Am4ncbwRUyCgdYkfuOzbi9p7JTx3LlzybLMnj27KidlaYcozw1FgIIMRSXO+7AkAkTWpEkTwR8+Q2wEDFmir6hZlhhtxJZlbCx5dEoCFGRKHnH/hI7fkCP+uBnsE4AsP/jgA8UTa/KA7TXXXCOQ5datW+0nwBgSigAF6WF1Y8gg/oAxhJDBeQLoZB9KlgMGDKAsnccdyBgpSI+qFS8WIMc+ffp4lIPEStaQZevWrdVqj0bLkrJMrOsg1tJSkLESc+D4Xr16KTlilhuG+BO4cOGCzJ07VyDLHDlyqLqoUKGCQJZffPFF/DPEFLUlQEHGuWowwS1aL5jwlsF7AoYs27Rpk0KWzzzzDGXpffV4ngMKMo5VgAkaIEcslcCgHwHI8sMPPxSzLMuXLy+Q5ZYtW/TLMHPkOgEK0nXEIpjB5q677lJyxFIFDP4gYMjy0ksvVXVHWfqj3pzMJQXpJM0QcWEZ1htvvFEtR4DlWRn8SQCybNu2rZhl2b9/f7Ys/VmdUeeagowaVewHYvwzFrPKnTu3rFq1KvYIeIaWBDC3plmWmFgEsox1YhEtC8dMpSBAQabA4dwHrBtdunRpNcyPHZSd46pbTIYsMS0dni9TlrrVkL38UJD2+IU8e/369VKgQAE1gmPPnj0hj+HO4BHApMYY826W5dNPP82WpY+rmoJ0uPI+/fRT1RH5hhtukMOHDzscO6PzCwFDlpidCS1LTF8HWW7atMkvRWA+RYSCdPAyQOdj/DHcdtttcvLkSQdjZlR+JgBZtm/fXk1lZ8iyX79+lKUPKpWCdKiSpk6dquTYrFkzh2JkNEEkgGntKEv/1CwF6UBdvfLKK0qOeP7EQALREjBkiSV50bIsW7asoGW5cePGaKPgcS4ToCBtAn7uuefUxf3YY4/ZjImnJzIByLJDhw5q/XJDlk899RRl6fFFQUHaqAD0fcPFjP/6DCTgFIH58+enkGWZMmUEstywYYNTSTCeKAlQkFGCSn1Y9+7dlRxHjBiR+it+JgHHCBiyvPzyy9X1Rlk6hjaqiCjIqDClPAgP2dFyfPnll1N+wU8k4CKBBQsWyEMPPSRmWT755JNsWbrInIKMEW7z5s2VHKdMmRLjmTycBJwjYMgSw1jxzxqjtiBLDFJgcI4ABRkly1OnTskdd9yhLkYsPcpAAroQgCw7duyoxvwbsuzbty9l6UAFUZBRQPzll1+kVq1aasW8JUuWRHEGDyEBbwhgxijK0jn2FGQElnv37hWst5wvXz5Zt25dhKP5NQnoQ8CQ5RVXXKHufEqVKiVoWfI6jr6OKMh0WG3btk2KFy8uJUuWlKSkpHSO5FckoDcByBLLfZhliQXjKMv0642CDMNn9erVkidPHqlcubIcOHAgzFHcTQL+I7Bw4cIUskQDgLIMXY8UZAguuICyZMkidevWld9//z3EEdxFAsEgYMgSjQG84DFkuXbt2mAU0GYpKMhUAGfPnq0ulDvvvFPOnDmT6lt+JIHgEli0aJF06tRJ3TkZsuzdu7cksiwpSNP1PmnSJCXHFi1amPZykwQSj0BqWZYoUUIgyzVr1iQUDAryv9X94osvKjmiiwQDCZDA/whAlo888ojkzZtX/Y0kkiwpSBEZOnSoqviePXv+76rgFgmQQBoCixcvTiPLJ554IrAty4QXJIZn4XnLgAED0lwM3EECJBCegCFL9BHG3xC6xEGW6AESlJDQguzSpYuq2NGjRwelPlkOEvCEAGTZuXNnNaDCkGWvXr18L8uEFWTr1q2VHF977TVPLigmSgJBJYDhuEGRZcIJ8sKFC9K0aVMlx2nTpgX1GmW5SEALAoYs8+fPr/7mihUrJmhZrlq1Sov8RcpEQgny+PHjcsstt0iGDBkEC74zkAAJxI8AlkR+9NFHxSxLvBjVWZYJI8gff/xRqlevrhZ1/+yzz+J3VTAlEiCBNARSy7Jo0aICWa5cuTLNsV7uSAhB7tq1S8qVKyeFChXiWsReXm1MmwRCEIAs8cK0QIEC6jZcJ1kGXpBbtmyRwoULqyU1d+7cGaJ6uIsESEAXAkuXLk0jyx49enjWsgy0IJcvX66W0axWrZocOnRIl2uA+SABEoiCgCHLggULqpZlkSJFBLJcsWJFFGc7c0hgBYl1hjNmzCj169eXP//80xlajIUESMATApBl165dJd6yDKQgZ8yYof7jNG7cWM6dO+dJhTJREiABdwgsW7YsjSwff/xxV1qWgRPkxIkTlRxbtWrlTu0wVhIgAW0IGLLEC1iM4MH7BsgSj9ecCIES5JgxYxQk9OJnIAESSCwC6L7XrVs31VvFkGX37t1tyTIwghw0aJCSI+asYyABEkhsAmZZNmzY0DKMQAgSM4jgP8bgwYMtg+CJJEACwSSwYcMGywXzvSAxRTzkOG7cOMsQeCIJkAAJhCLga0G2bNlSyfHNN98MVTbuIwESIAFbBHwpyH/++UcaNWqk5Dhz5kxbAHgyCZAACYQj4DtB/vHHH3LTTTdJ5syZZcGCBeHKxf0kQAIkYJuArwR58OBBqVKliuTOnduzsZm2iTMCEiAB3xDwjSB37NghpUuXFozH3Lp1q28AM6MkQAL+JeALQeI1PcZgVqhQQXbv3u1f2sw5CZCArwhoL0gMUs+RI4fUrFlTfv75Z1/BZWZJgAT8TUBrQc6dO1e9qb711lvlxIkT/ibN3JMACfiOgLaCfOedd5Qc77nnHt9BZYZJgASCQUBLQU6YMEHJsW3btsGgzFKQAAn4koB2ghw5cqSSI2blYCABEiABLwloJcj+/fsrOT711FNeMmHaJEACJKAIaCNITHKJSSeGDx/OqiEBEiABLQhoIcgOHTooOY4fP14LKMwECZAACYCA54Js3ry5kuPbb7/NGiEBEiABrQh4Jsi///5bGjRooOT4/vvvawWFmSEBEiABEPBEkL/++qvUrl1bsmXLJosXL2ZNkAAJkICWBOIuyH379knFihUlb968snbtWi2hMFMkQAIkAAJxFeRXX30lxYsXlxIlSkhSUhJrgARIgAS0JhA3Qa5Zs0a1GitVqiT79+/XGgozRwIkQAIgEBdBLlq0SLJmzSp16tSR3377jeRJgARIwBcEXBfk7Nmz1ZtqvLE+ffq0L6AwkyRAAiQAAq4KcvLkyUqO9913H2mTAAmQgO8IuCbIl156ScnxoYce8h0UZpgESIAEQMAVQQ4bNkzJsUePHqRMAiRAAr4l4LggMRMPJp145plnfAuFGScBEiABEHBUkF27dlVyHDVqFOmSAAmQgO8JOCbINm3aKDm++uqrvofCApAACZAACNgW5IULF6Rp06ZKjtOmTSNVEiABEggMAVuC/OuvvwQrDuKZ44cffhgYKCwICZAACYCAZUH+9NNPUqNGDbn00ktl2bJlpEkCJEACgSNgSZC7du2S8uXLS8GCBWXjxo2Bg8ICkQAJkAAIxCzIL774QgoXLixlypSRnTt3kiIJkAAJBJZATIJcsWKFXH755VK1alX5/vvvAwuFBSMBEiABEIhakPPnz5dMmTJJvXr15OjRo6RHAiRAAoEnEJUgZ8yYod5UN2rUSP7999/AQ2EBSYAESAAEIgryjTfeUHJ84IEHSIwESIAEEopAuoIcO3askuMjjzySUFBYWBIgARIAgXQFiTVkevfuTVIkQAIkkJAE0hVkQhJhoUmABEjgvwQoSF4KJEACJBCGAAUZBgx3kwAJkAAFyWuABEiABMIQoCDDgOFuEiABEqAgeQ2QAAmQQBgCFGQYMNxNAiRAAhQkrwESIAESCEOAggwDhrtJgARIgILkNUACJEACYQhQkGHAcDcJkAAJUJC8BkiABEggDAEKMgwY7iYBEiABCpLXAAmQAAmEIUBBhgHD3SRAAiTwf+yXF9GMFpQCAAAAAElFTkSuQmCC[/img][br][br]Select [b]all [/b]angles that are congruent to angle 1.