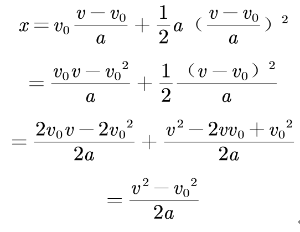下面是你初中时就学习过的正比例函数，若这里的横纵坐标分别为x、y，那么它的函数表达式可以写成y=kx. k是一个常量。数学中我们定义斜率为[math]k=\frac{\Delta y}{\Delta x}[/math]，你可以先拖动k的滑动条观察函数图像的变化。接着再拖动A点和B点，观察随着[math]\Delta x[/math]和[math]\Delta y[/math]的变化，k值是否会发生改变？[br]（答：不会变）[br][br][br]

若把横纵坐标分别换为时间t、位移x，那么它的函数表达式可以写成x=kt. k是一个常量。你可以先拖动k的滑动条观察函数图像的变化。接着再拖动A点和B点，观察随着[math]\Delta x[/math]和[math]\Delta y[/math]的变化，k值是否会发生改变？这里的k含义是什么？[br]（答：1.不会变。[br]2.由于速度的定义式为[math]v=\frac{\Delta x}{\Delta t}[/math]，所以这里k的含义是速度，因为速度一直不变，所以既可以说是瞬时速度也可以说是平均速度）[br][br][br]

那么如果x-t图像是一个曲线，我们怎么看速度呢？[br]如下图所示，当[math]\Delta t[/math]较大时，[math]\frac{\Delta x}{\Delta t}[/math]表示的是平均速度，同时也是图像中的割线斜率。[br]接下来请你拖动B点，让B点逐渐靠近A点，我们可以观察到[math]\Delta t[/math]逐渐变小，且此时割线越来越接近切线。两者的斜率也越来越接近，在极限意义上，两者严格相等。因此我们说在x-t图像中，割线斜率表示平均速度，切线斜率表示瞬时速度。

下面我们再来看看v-t图像，同样地，我们也从匀速直线运动开始出发。匀速直线运动的v-t图像很无聊，就一个平平的直线，因为任意时刻的速度都相等。

变速直线运动的v-t图像是什么样子的呢？很简单，随着t不同，v可能取到不同的值，一般地，就像下面这样歪歪扭扭的曲线。

上面那种歪歪扭扭的不好研究，所以我们一般先研究v虽然随着时间t在变化，但是均匀的变化着的，也就是像下面这样的图像，我们从图像可以看出斜率是定的，如果我们定义这个斜率为加速度a，那么就有[math]a=\frac{\Delta v}{\Delta t}[/math].[br]由此定义式出发，[math]\Delta v[/math]写成[math]v-v_0[/math]，[math]\Delta t[/math]就用时间t表示，我们就可以得到匀变速直线运动的基本公式1：[math]v=v_0+at[/math]

下面我们再来看看匀变速直线运动的基本公式2：[math]x=v_0t+\frac{1}{2}at^2[/math]是怎么来的。[br]想要知道怎么算变速运动的位移，首先我们要知道匀速直线运动的位移如何计算。由于匀速直线运动有x=vt，因此匀速直线运动的位移在v-t图像下就是与横轴包围的面积（横轴下方的面积取负，表示位移方向为负方向）

出于把未知问题转化为已知问题去解决的原则，我们想用匀速直线运动求位移的方法来求变速直线运动的位移，要想让这个想法变成现实，需要极限的思想，正式开始介绍方法之前，我们先来看一个小实验。下面球1做速度为1m/s的匀速直线运动，而球2初速度也是1m/s，但还有一个[math]1m\slash s^2[/math]的加速度，请你拖动滑动条，观察位移差的变化。你可以看到，当t越小时，两者的位移差越小，而且只要t可以任意的小，那么这个差值也可以任意的小。因此我们说在极限意义上，亦即[math]\Delta t\longrightarrow0[/math]时，两者的位移是相等的。所以我们可以用无穷多段匀速直线运动的位移和来代替不好求的变速直线运动的位移。

而无穷多段的匀速直线运动位移和，在几何意义上就是无穷多段矩形面积的和，拖动下面滑动条n（矩形数目），可以观察到随着分段越多，这个面积和越来越接近v-t图线与横轴包围的面积，因此直接算出梯形面积即可得到匀变速直线运动的位移。该梯形面积正好就可表示为[math]x=v_0t+\frac{1}{2}at^2[/math]，这样就得到了匀变速直线运动的基本公式2.

另外你也可以通过直接算出无穷个矩形面积和的暴力手段直接得到匀变速直线运动的公式，经过这样的一个过程你可以为学习定积分打下很好的基础。因为这个过程其实就是运用定积分的定义计算的过程。为了能研究等分n个区间（为了运算方便我们取n等分，最后再让n趋于无穷大）的矩形面积和，我们可以把这个面积之和用数学表达以便研究，具体过程如下：

有了两个运动学基本公式以后，我们会发现后面其他的很多公式都能通过这两个公式推出来。比如[math]v^2-v_0^2=2ax[/math]可以根据联立两个基本公式后消t得到.[br]具体过程如下：[br]由[math]v=v_0+at[/math]得[math]t=\frac{v-v_0}{a}[/math]，再将其带入[math]x=v_0t+\frac{1}{2}at^2[/math]中得：