Geogebra Institute - Day 1 Session 2 Challenges

bryantrcooper, May 24, 2023

Table of Contents

  1. Graphing Challenges
    1. Finding Intersection of Curves
    2. Finding Max and Mins of Functions
    3. Creating your own function
    4. Creating an input box

1.

Graphing Challenges

  • 1. Finding Intersection of Curves
  • 2. Finding Max and Mins of Functions
  • 3. Creating your own function
  • 4. Creating an input box

1.1.

Finding Intersection of Curves

Use the graphing calculator below to find the intersection of sin(x) and cos(x).
What are the intersection points between 0 and 2[math]\pi[/math]?
Wouldn't it be nice if we could change the axis to reflect radians instead of integers? We CAN!
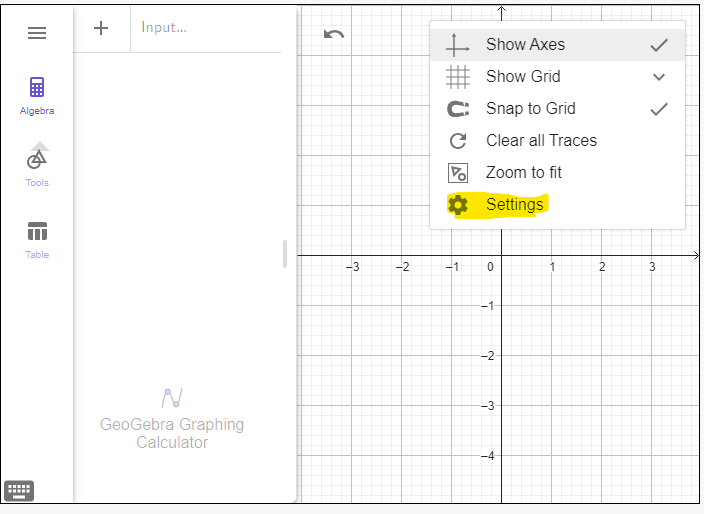
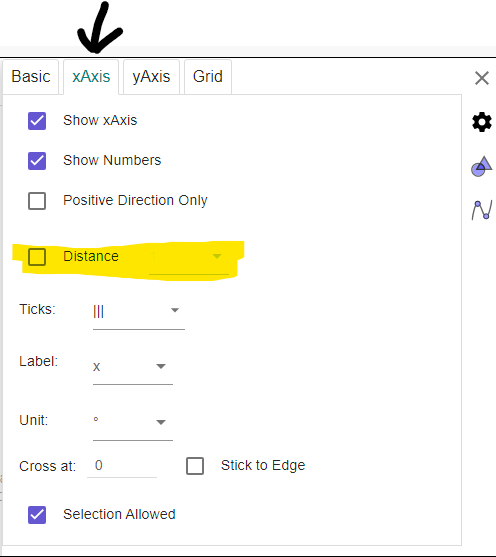
You can also change the distance by typing in the text box where the "1" is.
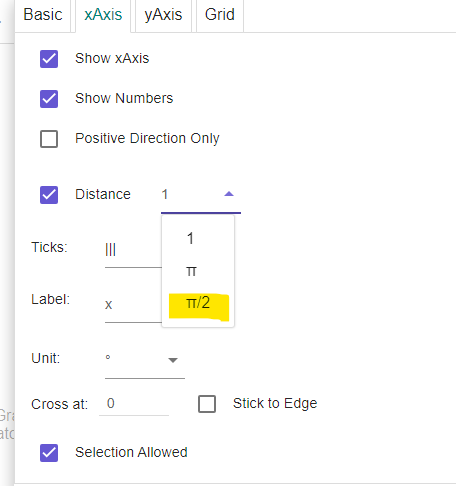
Using the graph from above, find the max and mins of sin(x) and cos(x).[br][br]Bonus: Try to find the max and min in more than one way!
What is the maximum of sin(x)?
Where is the minimum of [math]\cos\left(x\right)[/math]?
How can you use this in your classroom to help explain max and min concepts to students?
– bryantrcooper

1.2.

–

1.3.

–

1.4.

–

Information