Du wirst im Rahmen dieses ersten Praktikums erste Funktionen und Werkzeuge von GeoGebra kennenlernen und einsetzen. [br]Du wirst dabei in jedem Schritt eine neue Funktion kennenlernen, bevor du im letzten Schritt alles zusammenbringen wirst, um eine eigene Aufgabe zu erstellen.

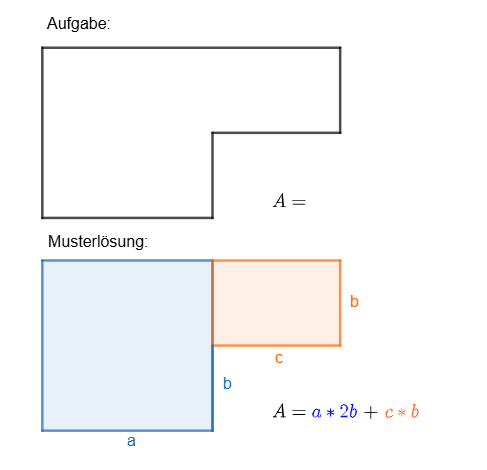
[b][u][size=200]Ziel[/size][/u][/b][br][br]Ziel des Praktikums ist es zu lernen, wie du eine Figur in GeoGebra erstellen und einfärben, sowie eine Beschriftung hinzufügen kannst. [br]Diese soll aus einem Term bestehen, der die erstellte Figur beschreibt. ( -> Term als "Bauplan")[br][br]Wie das am Ende aussehen kann, siehst du im angegebenen Beispiel.

[b][u][size=200]Aufgabe 1[/size][/u][/b][br][br]Im ersten Schritt lernst du verschiedene Möglichkeiten kennen, wie du eine geometrische Figur in GeoGebra erstellen kannst. [br][br]1) Du kannst im Reiter [i]Algebra[/i] neue Punkte hinzufügen, indem du sie nach dem Muster [i]A=(x,y)[/i] als neue Elemente einträgst. Überlege dir hierzu die passenden Koordinaten für dein gewünschtes Polygon. [br]Anschließend verbindest du die eingetragenen Punkte mit dem Werkzeug [i]Vieleck[/i].[br][br]2) Alternativ kannst du die Punkte auch mit dem Werkzeug [i]Punkt[/i] in die Ebene setzen. [br][br](Hinweis: Lass dir dafür das Koordinatengitter anzeigen, um parallele und orthogonale Seiten des Polygons einzuzeichnen. Zu der Einstellung gelangst du über einen Rechtsklick auf die Ebene.)[br][br]Du kannst die Punkte anschließend wieder mit dem [i]Vieleck[/i]-Werkzeug verbinden.[br][br]3) Eine dritte Option, für die du kein Koordinatengitter benötigst, ist zwei Punkte beliebig zu setzen ([i]Punkt[/i]) und alle folgenden Punkte mit den Werkzeugen [i]Senkrechte Gerade[/i] und [i]Parallele Gerade[/i] die weiteren Seiten des Polygons festzulegen. Nutze wieder das Werkzeug [i]Punkt[/i], um an den entsprechenden Stellen die Eckpunkte zu setzen und verbinde sie wie in 1) und 2).

[b][u][size=200]Aufgabe 2[br][/size][/u][/b][br]Später soll immer ein Teil des Polygons und der entsprechend zugehörige Teil des aufgestellten Terms farblich gleich gestaltet sein. Dafür müssen wir Teile der Figur anders einfärben. [br]Im oberen Applet wirst du feststellen, dass man ein Vieleck immer nur im gesamten einfärben kann. Daher baust du deine Figur auf der nächsten Übungsfläche nochmal nach. [br]Überlege dir vorher, wie du es geschickt unterteilen kannst, um anschließend den Term für den Flächeninhalt (und eventuell den Umfang) aufstellen zu können. [br]Verbinde die Eckpunkte der Teilfiguren folglich immer mit einem eigenen "Vieleck". [br][br]1) Diese Teilfiguren kannst du dann über das Farbtopf-Symbol einfärben, das bei einem Linksklick auf das Polygon erscheint. [br][br]2) Eine andere Möglichkeit ist es im Reiter "Algebra" das Polygon zu suchen und nach dem folgenden Pfad einzufärben. (Hinweis: Hier hast du eine größere Farbpalette zur Auswahl.)[br]->Objekt "Polygon A, B, C, D" suchen ->drei Punkte ->Einstellungen -> Farbe. [br]Wähle nun die gewünschte Farbe aus und schließe das Fenster wieder. Du hast nun das Polygon samt seiner Seiten gefärbt. [br]Die Seiten kannst du auch einzeln umfärben. Suche hierfür nach der entsprechenden "Strecke A, B" und gehe danach gleich vor wie beim Polygon.

[b][u][size=200]Aufgabe 3[br][br][/size][/u][/b]Prima, jetzt hast du ein Polygon, das unterteilt und unterschiedlich eingefärbt ist![br]Im nächsten Schritt soll der Term eingefügt werden, der den Flächeninhalt des Polygons beschreibt. Dieser soll farblich so gestaltet sein, dass auf den ersten Blick erkennbar ist, zu welchem Teil der Figur er gehört. [br][br]Um den Term aufstellen zu können, musst du zunächst die Seiten des Polygons beschriften. [br]Das machst du, indem du die einzelnen Seiten anklickst, einen Namen wählst und diesen anschließend anzeigen lässt.[br]Das kannst du an dem gegebenen Rechteck üben.[br][br]Dafür lernst du das Werkzeug "Textfeld" kennen. Dieses findest du bei den Werkzeugen unter der Rubrik "Medien". Wähle es aus und klicke dann an die gewünschte Stelle auf der Übungsfläche 3, an der das Textfeld später stehen soll. (Hinweis: Du kannst es auch im Nachgang noch verschieben.)[br]Es öffnet sich ein Fenster, in dem du oben [b]B [/b]für fett, [i]I[/i] für kursiv und [i]Serifen-Schrift[/i] für die Veränderung der Schriftart findest. Diese Schaltflächen verändern aber immer das gesamte Textfeld.[br]Das Eingeben einer [i]LaTeX Formel [/i]ermöglicht es uns einzelne Teile der Schrift unterschiedlich einzufärben. [br][br]Die Eingabe erfolgt so: [br][br]\ -> Beginn des Befehls[br]Befehl -> der Befehl selbst, in unserem Fall [i]color[br][/i]{} -> wie soll der Befehl ausgeführt werden[br]{} -> worauf soll der Befehl ausgeführt werden[br][br]So ergibt sich z.B.[br][br]\color{blue}{1+2}\color{red}{=3}[br][br]Das Ergebnis wäre "1+2" in blau und "=3" in roter Schrift. [br][br]Mögliche Farben sind: red, green, blue, cyan, magenta, yellow, black, gray, white, brown, orange, purple

[b][u][size=200]Aufgabe 4[/size][/u][/b][br][br]Super gemacht! Du hast jetzt alle Funktionen kennengelernt, um selbst eine schöne Aufgabe mitsamt Musterlösung zum Aufstellen von Termen zu einer geometrischen Form zu erstellen. [br]Die Aufgabe für deine Schülerinnen und Schüler könnte so lauten: [br]"Stelle eine Term für den Flächeninhalt des Polygons auf. Unterteile das gegebene Polygon dafür in passende Teilflächen und markiere farbig welcher Teil des Terms welchen Teil des Polygons beschreibt. "[br]Deine Aufgabe ist es ein Polygon für diese Aufgabe zu erstellen. [br][br]Im zweiten Schritt kannst du dann eine Musterlösung erstellen, indem du die Aufgabe selbst in GeoGebra bearbeitest, das Polygon unterteilst, die Seiten beschriftest und einen farblich passenden Term einfügst.[br][br]Nutze dafür das erlangte Wissen aus den Aufgaben 1-3. [br][br]Viel Erfolg!

Schön, dass du da bist! Bereit loszulegen?[br][size=150][size=200][size=100]In dieser GeoGebra-Aktivität lernst du den Umgang mit Schiebereglern und Kontrollkästchen. [br][/size][br][size=100][u][b]Was sind Kontrollkästchen in GeoGebra?[/b][/u][br]Ein [b]Kontrollkästchen[/b] in GeoGebra ist ein interaktives Werkzeug, mit dem Benutzer:innen bestimmte Objekte oder Eigenschaften  [b]ein- oder ausblenden[/b] bzw. [b]steuern[/b] können. Es wird häufig verwendet, um die [b]Sichtbarkeit[/b] von Objekten zu steuern, [b]Animationen[/b] zu starten oder andere [b]dynamische[/b] [b]Funktionen[/b] zu aktivieren.[br][/size][size=100][br][u][b]Was sind Schieberegler in GeoGebra?[/b][/u][/size][br][size=100][b]Schieberegler[/b] können verwendet werden, um die Werte von [b]Variablen[/b] [b]kontinuierlich[/b] zu [b]ändern[/b], z.B. die Parameter in einer Gleichung, wie die Steigung oder der y-Achsenabschnitt einer Geradengleichung y = mx + c. Wenn der Schieberegler bewegt wird, aktualisiert GeoGebra automatisch alle Objekte und Funktionen, die von diesem Parameter abhängen, und zeigt die [b]Änderungen in Echtzeit[/b] an. [/size][br][br][size=100]Ziel ist es, dass du [b]Schieberegler[/b] und [b]Kontrollkästchen[/b] [b]erstellen[/b] und [b]anpassen[/b] kannst. Außerdem wirst du auch anhand eines Beispiels lernen, wie man beide Kontrollkästchen und Schieberegler [b]miteinander verknüpfen[/b] kann. Zunächst fangen wir aber mit den [b]Grundlagen[/b] des [b]Grafikrechners[/b] von GeoGebra an und bauen dein Wissen und deine Fähigkeiten Schritt für Schritt auf. [br][br][b]Los gehts! Viel Spaß![/b][/size][/size][/size]

Ziel der Aufgabe ist es, zunächst einige [b]grundlegende Anwendungen[/b] des Grafikrechners von GeoGebra kennen zu lernen. [br][br][b]Erstelle[/b] die zwei[b] Geraden f und g[/b] im Grafikrechner.[br][br][list][*][b]g(x) = -1,3x - 15[br][/b][/*][*][b]f(x) = 2x - 3[/b][/*][/list][br]Verwende dafür deine eigene Tastatur oder die GeoGebra-Tastatur.[br][br]1) Als erstes kannst du in den [b]allgemeinen Einstellungen[/b] durch Klicken auf das Zahnrad oben rechts zum einen die Achsen ein- und ausblenden und zum anderen unter [b]Einstellungen[/b] die [b]Skalierung[/b] und [b]Linienart[/b] der Achsen verändern. [br][br]2) Nun kannst du die beiden [b]Geraden[/b] f und g [b]bearbeiten[/b], indem du die [b]Einstellungen[/b] [b]öffnest[/b]. [br]Hier gibt es zwei Möglichkeiten:[b][br][/b][list][*]Du klickst [b]direkt[/b] auf den [b]Graphen[/b]. Dann öffnet sich zunächst eine kleine Auswahl an Optionen. Wenn du hier auf die [b]drei Punkte[/b] und anschließend auf [b][i]Einstellungen[/i][/b] klickst, öffnet sich rechts ein Menü mit mehr Auswahlmöglichkeiten.[/*][*]Oder du klickst auf die [b]drei Punkte[/b] neben der Eingabe der Funktionsgleichung und anschließend auf [b]Einstellungen. [/b]Es öffnet sich rechts ein Menü. [/*][/list] Probiere einmal aus, die [b]Farbe[/b], [b]Dicke[/b] und [b]Linienart[/b] zu [b]ändern[/b].[br][br]3) In diesem Einstellungsmenü kannst du außerdem die [b]Funktionsgleichungen[/b] der beiden Geraden im Koordinatensystem [b]anzeigen[/b] lassen, indem du das Häkchen bei [b][i]Beschichtung anzeigen[/i][/b] setzt und [b][i]Name & Wert[/i][/b] auswählst.[br][br]4) Du kannst auch[b] spezielle Punkte[/b] und eine [b]Wertetabelle[/b] anzeigen lassen, indem du auf die [b]drei Punkte[/b] neben der Eingabe der Funktionsgleichung klickst. [br]Probiere es aus und lasse dir eine [b]Wertetabelle[/b] im Intervall [b]von[/b] [b]-4 bis -4 [/b]anzeigen.[br][br][br][br][br][br]

Ziel der Aufgabe ist es, ein [b]Kontrollkästchen[/b] zu einem Schnittpunkt zu erstellen.[br][br]1) Bestimme den Schnittpunkt der beiden Geraden mit dem [b]Schnittpunkt-Tool[/b] [icon]/images/ggb/toolbar/mode_intersect.png[/icon]. Klicke dafür das Schnittpunkt-Tool an und danach die beiden Geraden.[br][br]2) Um dir die [b]Koordinaten des Schnittpunktes[/b] anzuzeigen, gehe zu den Einstellungen des Schnittpunktes (gleiche Vorgehensweise wie bei Aufgabe 1.2) und ändere die [b]Beschriftung in [i]Name & Wert[/i][/b].[br][br]3) Wir wollen nun ein [b]Kontrollkästchen[/b] erstellen, mit dem der Schnittpunkt ein- und ausgeblendet werden kann. Öffne hierfür den [b]Reiter [i]Werkzeuge[/i][/b]. Klicke auf das das [b]Kontrollkästchen-Tool[/b][icon]/images/ggb/toolbar/mode_showcheckbox.png[/icon] und platziere es im Koordinatensystem. Ein Fenster öffnet sich. [b]Beschrifte[/b] das Kontrollkästchen, beispielsweise mit [b][i]Schnittpunkt,[/i][/b] und wähle aus dem [b]Dropdown-Menü[/b] das [b]Objekt[/b] aus, mit dem du das Kontrollkästchen [b]verknüpfen[/b] möchtest. In unserem Fall ist das der [b]Schnittpunkt[/b].[br][br]Jetzt hast du ein Kontrollkästchen, auf das du klicken kannst, um den Schnittpunkt anzuzeigen. Funktioniert es?

In dieser Aufgabe lernst du, wie du in Geogebra einen [b]Schieberegler[/b] [b]einfügst[/b] und wie du diesen für deine Zwecke [b]anpassen[/b] kannst. [br][br][b]Ziel[/b] der Aufgabe ist es, die beiden [b]Parameter einer Geradengleichung[/b], die Steigung und den y-Achsenabschnitt, durch einen [b]Schieberegler[/b] darzustellen. Es gibt unterschiedliche Möglichkeiten, einen Schieberegler zu konstruieren. Probiere die Möglichkeiten anhand der folgenden Anleitung aus.[code][br][/code][br]1) Zunächst wollen wir den y-Achsenabschnitt einer Geraden f(x) durch einen Schieberegler modellieren. Gib hierzu im [b]Reiter [i]Algebra[/i][/b] unter [b][i]Eingabe[/i][/b] den Funktionsterm [b]f(x)= 2x + c[/b] ein und klicke [b]Enter[/b]. Es erscheint eine Gerade im Koordinatensystem sowie ein Schieberegler für den Parameter c im Eingabefeld. Durch [b]Anklicken des Kreises[/b] vor dem Schieberegler erscheint auch dieser im Koordinatensystem.[code][br][/code][br]2) Für die zweite Variante wollen wir die Steigung m einer weiteren Geraden als Schieberegler darstellen: [br]Klicke unter dem [b]Reiter [i]Werkzeuge[/i][/b] auf das [b]Schieberegler-Tool[/b] [icon]/images/ggb/toolbar/mode_slider.png[/icon]. Klicke anschließend an die [b]Position im Koordinatensystem[/b], an die der Schieberegler eingefügt werden soll. Ein Fenster öffnet sich:[br][list][*]GeoGebra schlägt dir unter [i][b]Name[/b][/i] einen Namen für deine [b]Variable[/b] vor. Du kannst diesen aber beliebig ändern. Nenne  nun deine Variable [b]m[/b]. [/*][*]Das [b][i]=1[/i][/b] bedeutet, dass der [b]Startwert[/b] [b]der Variable[/b] nach dem Einfügen des Schiebereglers 1 ist. Auch diesen Wert kannst du beliebig ändern. [/*][*]Außerdem kannst du hier auswählen, ob der Schieberegler [b]rationale Zahlen[/b] ([i]Zahl[/i]), [b]ganze Zahlen [/b]oder [b]Winkel[/b] anzeigen soll. [/*][/list][br]Klicke anschließend auf [i][b]ok[/b][/i]. Sobald du nun den Variablennamen in einer Funktionsvorschrift verwendest, wird der Schieberegler mit dieser verknüpft. [b]Füge[/b] also unter dem [b]Reiter [i]Algebra[/i][/b] eine [b]Geradengleichung g(x)[/b] ein, so dass der erzeugte Schieberegler die Steigung dieser Geraden modelliert. Der[b] y-Achsenabschnitt [/b]soll [b]2[/b] sein. Bewege den Schieberegler zur Kontrolle vor und zurück.

[b]Im[/b] [b]folgenden Applet[/b] siehst du, wie dein oberes Applet [b]am Ende von Aufgabe 2[/b] aussehen soll.[br]Nun wollen wir die beiden [b]Schieberegler[/b] noch etwas [b]anpassen[/b]. [br]Dazu öffnen wir die [b]Eigenschaften[/b] des [b]Schiebereglers[/b], der den y-Achsenabschnitt [b]c[/b] von f(x) modelliert (z.B. Rechtsklick auf den Schieberegler [math]\longrightarrow[/math] Einstellungen).[br][list=1][*]Unter dem [b]Reiter [i]Grundeinstellungen[/i][/b] kannst du unter [i][b]Beschriftung[/b] [b]anzeigen[/b] [/i]wählen, ob dir der [b]Wert und/oder [/b]der[b] Name[/b] des Schiebereglers angezeigt werden soll. [b]Wähle [i]Name & Wert[/i][/b] aus.[br][/*][*]Unter dem [b]Reiter [i]Schieberegler[/i] [/b]kannst du den [b]maximalen und minimalen Wert [/b]festlegen, den deine Variable annehmen soll. Ändere das Intervall auf [b]-10 bis 10.[/b][br][/*][*]Wähle als nächstes die [b]Schrittweite 0,2[/b].[br][/*][*]Außerdem wollen wir den Schieberegler [b]vertikal[/b] ausrichten und ihn [b]fixieren[/b]. Diese Optionen findest du ebenfalls hier.[br][/*][*]Wähle im letzten Schritt noch eine [b]passende Farbe[/b] für den Schieberegler aus.[br][/*][/list]

Die Ausgangssituation des folgenden Applets dient wieder als [b]Lösungskontrolle[/b] der [b]vorherigen[/b] [b]Aufgabe[/b]. [br][br]Geogebra bietet die Möglichkeit den [b]Schieberegler[/b] zu [b]animieren[/b]. Wenn die Animation gestartet wird, bewegt sich der Schieberegler automatisch vor und zurück. [br][br]a) Zuerst wollen wir die [b]Animation[/b] [b]starten[/b]. Dazu gibt es [b]zwei[/b] [b]Möglichkeiten[/b]. Probiere beide aus:[br][list=1][*]Klicke auf das [b]Play-Symbol im Algebra[/b][b]-[/b][b]Tab[/b].[/*][*]Öffne die die [b]Einstellungen[/b] des [b]Schiebereglers[/b] und gehe zu [i][b]Grundeinstellungen[/b].[/i] [b]Aktiviere[/b] das [b]Häkchen[/b] bei [i][b]Animation[/b][/i]. [/*][/list][br]b) Du kannst die [b]Animation[/b] auch noch [b]anpassen[/b]: Öffne hierfür in die [b]Einstellungen[/b] des [b]Schiebereglers[/b] und gehe zum [b]Reiter [/b][i][b]Schieberegler[/b]:[/i][br][list=1][*]Hier kannst du die [b]Geschwindigkeit[/b] [b]erhöhen[/b] oder [b]verringern[/b]. [b]Stelle[/b] die Geschwindigkeit auf [b]0,5 [/b]ein.[/*][*]Außerdem kannst du auswählen, wie sich die [b]Animation[/b] des Schiebereglers [b]wiederholen[/b] soll. [b]Wähle[/b] unter Wiederholen [i][b]Zunehmend[/b][/i] und [b]beobachte[/b], was passiert, wenn du die Animation startest. [/*][/list][br]c) Im letzten Schritt wollen wir nun noch ein [b]Kontrollkästchen[/b] einfügen, das die [b]Animation[/b] [b]startet[/b] und [b]stoppt[/b]. Gehe wie folgt vor: [br][list=1][*]Gehe zum [b]Reiter [i]Werkzeuge[/i][/b] und füge mit dem [b]Kontrollkästchen-Werkzeug[/b] [icon]/images/ggb/toolbar/mode_showcheckbox.png[/icon]ein Kontrollkästchen ein. [br][/*][*][b]Nenne[/b] es [i][b]Start[/b][/i] und drücke auf [b][i]OK[/i][/b]. [/*][*]In der [b]Algebra-Ansicht[/b] erscheint das [b]Kontrollkästchen[/b] unter einem [b]anderen[/b] [b]Namen[/b] auf (beispielsweise b). [b]Merke[/b] dir diesen Namen.[/*][*]Öffnes nun die [b]Einstellungen[/b] des [b]Kontrollkästchens[/b] und wähle den [b]Reiter [i]Skripting[/i][/b] aus. [/*][*]Füge nun folgendes in das [b]Textfeld[/b] ein: [b][color=#980000]if([i]Name des Kontrollkästchens[/i], StartAnimation([i]Name des Schiebereglers[/i], true), StartAnimation([i]Name des Schiebereglers[/i], false))[/color][/b][/*][*][b]Klicke[/b] auf das [b]Kontrollkästchen[/b] und [b]überprüfe[/b], ob die Animation des Schiebereglers  nun startet und stoppt. [/*][/list]

Erstelle eine [b]eigene[/b] [b]Aufgabe[/b], die du im Matheunterricht in der [b]Einheit zu linearen Funktionen[/b] bzw. [b]linearen Gleichungen[/b] einsetzen könntest. [b]Formuliere[/b] hierzu eine [b]Aufgabenstellung[/b] für die Schüler:innen sowie das [b]zugehörige Applet, [/b]anhand dessen die Schüler:innen die Aufgabe lösen sollen. Die Aufgabe soll einen [b]Schieberegler[/b] sowie ein [b]Kontrollkästchen[/b] enthalten.