5.2 Circumcenters & Incenters

Debra Schneider, Dec 31, 2017

Find circumcenters (perpendicular bisectors intersection) and incenters (angle bisectors intersection) in an acute, right and obtuse triangles.

Table of Contents

  1. Perpendicular Bisector
    1. Acute Triangle
    2. Right Triangle
    3. Obtuse Triangle
  2. Circumcenter
    1. Circumcenter
    2. Circle Around a Triangle
    3. Circumcenter in a Right Triangle
  3. Angle Bisector
    1. Acute Triangle
    2. Right Triangle
    3. Obtuse Triangle
  4. Incenter
    1. Incenter
    2. Put a Circle in a Triangle
  5. Challenge
    1. Challenge #1
    2. Challenge 2
    3. Find Circumcenter with Algebra

1.

Perpendicular Bisector

  • 1. Acute Triangle
  • 2. Right Triangle
  • 3. Obtuse Triangle

1.1.

Acute Triangle

How to construct a perpendicular bisector in geogebra.
Construct perpendicular bisectors on each side of the triangle.[br][br]Watch this video from 0:55 to 1:08[br]https://youtu.be/bUbi5SmHyjg
Once you construct a perpendicular bisector on each side of the triangle, what do you observe?[br][br]Move the triangle around. Move the slider.[br]Does your observation still hold?[br]
– Debra Schneider

1.2.

–

1.3.

–

2.

Circumcenter

  • 1. Circumcenter
  • 2. Circle Around a Triangle
  • 3. Circumcenter in a Right Triangle

2.1.

Circumcenter

Move the vertices of the triangle to discover the properties of the circumcenter.
What are the properties of the circumcenter?
– Debra Schneider

2.2.

–

2.3.

–

3.

Angle Bisector

  • 1. Acute Triangle
  • 2. Right Triangle
  • 3. Obtuse Triangle

3.1.

Acute Triangle

How to find the angle bisector.
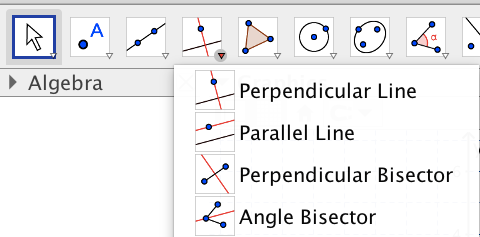
You find the angle bisect tool here:[br]
To bisect an angle
[list][*]Selecting three points [i]A[/i], [i]B[/i], and [i]C[/i] produces the angle bisector of the enclosed angle, where point [i]B[/i] is the apex.[/*][/list]
Bisect each angle of the triangle.
Once you construct a perpendicular bisector on each side of the triangle, what do you observe?[br][br]Move the triangle around. Move the slider.[br]Does your observation still hold?
– Debra Schneider

3.2.

–

3.3.

–

4.

Incenter

  • 1. Incenter
  • 2. Put a Circle in a Triangle

4.1.

Incenter

Move around points.
Describe the properties of the incenter.
– Debra Schneider

4.2.

–

5.

Challenge

  • 1. Challenge #1
  • 2. Challenge 2
  • 3. Find Circumcenter with Algebra

5.1.

Challenge #1

I found this question on the internet, "Let ABC be a triangle. Let B' and C' denotes respectively the reflection of B and C in the internal angle bisectors of angle A. How do I prove that the triangles ABC and AB'C' have same incenter?"[br][br]Use geogebra to prove or refute this claim.[br]Start by investigating.
– Debra Schneider

5.2.

–

5.3.

–

Information