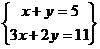
Resolución gráfica de sistemas de dos ecuaciones lineales con dos incógnitas.
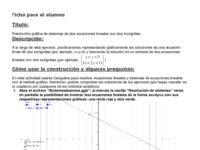
A lo largo de este ejercicio, practicaremos representando gráficamente las soluciones de una ecuación lineal de dos incógnitas (por ejemplo, x+y=5) y buscando la solución de un sistema de dos ecuaciones lineales con dos incógnitas.
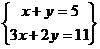
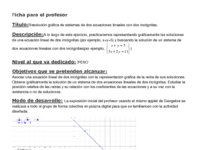
En esta actividad usarás Geogebra para resolver ecuaciones lineales y sistemas de ecuaciones lineales con el método gráfico. Asimismo, podrás comprobar las soluciones de los ejercicios que hayas resuelto en tu cuaderno por cualquiera de los métodos analíticos.[br]1.Abre el archivo “Sistemasalumnos.ggb”; si marcas la casilla “Resolución de sistemas” verás en pantalla la posibilidad de mostrar dos ecuaciones lineales de la forma ax+by=c con sus respectivas representaciones gráficas: una recta roja y otra verde. [br] [br][br] [br]a)Usando los deslizadores sobre cada ecuación, cambia los valores de a , de b y de c en ambas ecuaciones. Observa que, al modificarlos, el programa traza automáticamente las rectas correspondientes.[br][br][br][br][br]b)Da los valores: b=b’. ¿Cómo son las rectas cuando ambas ecuaciones tienen el mismo valor en a y a’?[br] [br] [br][br]c) Y cuando además de b=b’, a=a’. ¿Qué pasa con las rectas si tienen el mismo valor en c y c’?[br][br] [br][br]2. Cambia los valores de a, b, c, a’, b’, c’ para obtener el siguiente sistema de ecuaciones.[br] [br]a) Explica por qué las ecuaciones anteriores determinan que las respectivas rectas se corten en un punto.[br]b) ¿Hay algún punto en el plano que solucione el sistema de ecuaciones, es decir, cuyas coordenadas [br](x, y) hagan verdaderas ambas igualdades? Justifica tu respuesta.[br][br][br][br][br][br][br][br][br][br][br][br][br]3. Desmarca las casillas ”Primera ecuación” y “Segunda ecuación” y marca la casilla “Sistema” para encontrar en verde el punto donde se cruzan ambas rectas. Observa las coordenadas del Punto verde V[br] [br]a) Escribe las coordenadas del punto donde se intersecan las rectas.[br]Coordenada en x: Coordenada en y: [br]b) Verifica que esos valores de x e y resuelven ambas ecuaciones. Explica por qué.[br]c) Cambia los valores de a, b, c, a’, b’, c’ para generar un sistema de ecuaciones sin solución. Explica tu procedimiento.[br]d) Inventa un sistema de ecuaciones cuya solución sea el punto (1, 1). Escríbelo a continuación y explica cómo lo obtuviste.[br]e) Inventa dos sistemas de ecuaciones: uno que sí tenga solución y otro que no, e intercámbialos con un compañero para que intente resolverlos. Comentad cómo encontrasteis la solución de uno de los sistemas, y por qué el otro carece de ella. Anotad vuestras conclusiones.