Ensino de Funções Exponenciais

Felipe Morais Peixoto, 7/5/2025

Função Exponencial

Tabla de Contenidos

  1. Introdução.
    1. Introdução
  2. Definição.
    1. Definição:
  3. Restrições.
    1. Restrição para os valores da base:
  4. Propriedades importantes de potência.
    1. Propriedades das Potências
  5. Gráfico.
    1. Condições para construção de gráfico:
  6. Transformações gráficas.
    1. 1. Translação Vertical:
    2. 2. Translação horizontal:
    3. 3. Deformação ou Dilatação Horizontal:
    4. 4. Dilatação ou Deformação Vertical
  7. Questões Resolvidas
    1. Questões Resolvidas:
  8. Questões sobre função exponencial.
    1. Questões de nível fácil.
    2. Questões de nível médio.

1.

Introdução.

Uma breve introdução do ensino de funções.

  • 1. Introdução

1.1.

Introdução

A função exponencial é um dos conceitos matemáticos mais importantes e amplamente aplicados em diversas áreas do conhecimento, como física, biologia, economia e tecnologia. Em termos simples, ela descreve situações em que uma quantidade cresce (ou decresce) proporcionalmente ao seu valor atual, o que é representado por expressões do tipo [math]f\left(x\right)=a^x[/math], com [math]a>0[/math]e [math]a\ne1[/math]. Esse tipo de função modela fenômenos como crescimento populacional, juros compostos, decaimento radioativo e propagação de doenças.[br][br]Historicamente, o estudo das funções exponenciais tem raízes na antiguidade, mas seu desenvolvimento mais estruturado começou no século XVII, com o matemático escocês John Napier, que introduziu os logaritmos para facilitar cálculos multiplicativos complexos. Pouco tempo depois, Jakob Bernoulli explorou a ideia de crescimento contínuo ao estudar o problema dos juros compostos, o que levou à descoberta do número [math][/math] (aproximadamente 2,718), base da função exponencial natural. No século XVIII, o matemático suíço Leonhard Euler formalizou a função exponencial como a base de muitos desenvolvimentos na análise matemática, estabelecendo uma notação clara e relacionando-a com outras funções fundamentais, como os logaritmos e as funções trigonométricas.[br][br]Hoje, a função exponencial é essencial para a modelagem matemática de fenômenos dinâmicos, permitindo compreender e prever comportamentos em sistemas complexos. Ao longo deste conteúdo, exploraremos suas propriedades, gráficos, aplicações e como resolvê-la em diferentes contextos.
– Felipe Morais Peixoto

2.

Definição.

  • 1. Definição:

2.1.

Definição:

[size=200][size=100]Dado um número real [math]a[/math] ( com [math]a>0[/math] e [math]a\ne1[/math]), denomina-se função exponencial de[br]base [math]a[/math], uma função [math]f[/math] de [math]\mathbb{R}[/math] em [math]\mathbb{R}^+[/math] definida por [math]f\left(x\right)=a^x[/math] ou [math]y=a^x[/math][/size][/size]
[size=100]Em símbolos:[br][math]f:\mathbb{R}\longrightarrow\mathbb{R}^+[/math][br][/size][math]x\mapsto a^x[/math]
PROPRIEDADES:
1) [math]a^x\cdot a^y=a^{x+y}[/math][br]2) [math]a^1=a[/math][br]3) Se [math]a>1[/math] a função [math]f\left(x\right)=a^x[/math] é crescente.[br]4) Se 0 é decrescente.[br]5) A função [math]f:\mathbb{R}\longrightarrow\mathbb{R}[/math], definida por [math]f\left(x\right)=a^x[/math], é ilimitada superiormente.[br]6) A função exponencial é injetiva.[br]7) A função exponencial é contínua.[br]8) A função exponencial [math]f:\mathbb{R}\longrightarrow\mathbb{R}^{\ast}_+[/math], [math]f\left(x\right)=a^x[/math], com a>1 ou 0<a<1, é sobrejetiva.[br]9) A função exponencial, nas condições acima, é bijetiva, logo, admite função inversa (função logarítmica).
– Felipe Morais Peixoto

3.

Restrições.

  • 1. Restrição para os valores da base:

3.1.

Restrição para os valores da base:

1. Restrição para os valores da base:
Relembrando conceito de função:[br]Função é uma relação onde cada elemento (x) de um conjunto (domínio) obedece uma regra a um único elemento de outro conjunto (contradomínio). Para cada valor do domínio, podemos determinar um único valor do contradomínio.[br][br]Com isso para valores de [math]a<0[/math] não teríamos função bem definida para o conjunto dos números [math]\mathbb{R}[/math] como domínio.[br]Por exemplo: [br][math]f\left(x\right)=\left(-2\right)^x[/math] não representaria uma função [math]f:\mathbb{R}\longrightarrow\mathbb{R}[/math], pois para [math]f\left(-2\right)=\left(-2\right)^{-2}=\sqrt{-2}\notin\mathbb{R}[/math], ou seja, esse valor do domínio não teria imagem.[br][br]Para [math]a=0[/math] ou [math]a=1[/math] a função seria constante [math]f\left(x\right)=1^x=1[/math] e [math]f\left(x\right)=0^x=0[/math], para [math]x\ne0[/math], funções já estudadas anteriormente.[br][br]
1ª Questão:
Para que valores de [b]m[/b] a função [math]f\left(x\right)=\left(m-3\right)^x[/math] é uma função definida em [math]\mathbb{R}[/math]?
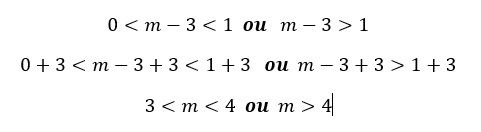
Para entender melhor!
– Felipe Morais Peixoto

4.

Propriedades importantes de potência.

  • 1. Propriedades das Potências

4.1.

Propriedades das Potências

Conhecendo as propriedades da potenciação
Produto de potências de mesma base:[br] Um produto de potências de mesma base pode ser simplificado escrevendo-o como uma única potência. Neste caso, mantemos a base e somamos os expoentes.[br][br]Quociente de potências de mesma base:[br] Um quociente de potências de mesma base pode ser simplificado escrevendo-o como uma única potência, desde que o expoente do dividendo seja maior ou igual ao expoente do divisor. Para isso, conservamos a base e subtraímos os expoentes.[br][br]Potência de uma potência:[br] Uma potência de uma potência pode ser simplificada escrevendo-a como uma única potência. Para isso, conservamos a base e multiplicamos os expoentes.[br][br]Potência de um produto:[br] Para elevar um produto de dois ou mais números racionais a um expoente, elevamos cada fator a esse expoente.[br][br]Potência de um expoente com número negativo:[br] Para elevar a um número negativo, invertemos a base.[br][br]Potência de um número racional (fração ou decimal):[br] Para elevar uma base a uma fração no expoente, transformamos a expressão em uma raiz. O denominador da fração se torna o índice da raiz, enquanto o numerador permanece como o expoente dentro da raiz.
Exemplos
– IGOR DAMASCENO DE ALMEIDA, Carlos Henrique Rocha Serra

5.

Gráfico.

  • 1. Condições para construção de gráfico:

5.1.

Condições para construção de gráfico:

Condições para construção de gráfico:
Para uma função exponencial nos restou 2 possibilidades [math]a\in\left(0,1\right)[/math] ou [math]a>1[/math]
Caso 1:[br]Para 0<a<1, a função é decrescente.
Caso 2:[br]Para a>1, a função é crescente.
– Felipe Morais Peixoto

6.

Transformações gráficas.

  • 1. 1. Translação Vertical:
  • 2. 2. Translação horizontal:
  • 3. 3. Deformação ou Dilatação Horizontal:
  • 4. 4. Dilatação ou Deformação Vertical

6.1.

1. Translação Vertical:

Exemplo:[br][math]f\left(x\right)=2^x+p[/math]
Note que ao variar o valor de [b]p[/b] a função sofre translação na vertical.
– Felipe Morais Peixoto

6.2.

–

6.3.

–

6.4.

–

7.

Questões Resolvidas

  • 1. Questões Resolvidas:

7.1.

Questões Resolvidas:

Questão-01 - (UERJ/2017)
[br][br]Observe o[br]plano cartesiano a seguir, no qual estão representados os gráficos das funções[br]definidas por [img width=53,height=20]data:image/wmf;base64,R0lGODlhQgAZAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABQA9ABAAhQAAAAAAAAAAHR0AAAAAMx0AMgAcSB0dSAAzWh0zWh1GbDMAADIAHTIAMjMeRzNGRjNbgEgcAEgdHUceM1ozAFozHVtISEhZf1l/WUhuW11/f0huf2xGHW5bNW5dXX9/XX9uSGaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwa0QIBwSCwaj8ikUhghLJ/QqBRACQimWGMkABgkJ0UFIAIQLSFYUYBrfBQtyQXxsGRkhQtE0c5cW4VgQwtoQoRJZncABkUYb0dqa04NQ1tXC1dDBXeITHpeSAGLeGicQhRDG0WGU6tYckKigmxEZJR+fnpGCYmjABxHn2FYgbyvikUOAE60tLdruUMVvIKGqUKTsLy/QqVTA89UtkLfsdBPVX7L00KaShLr8NlItfHwu0an9VNBADs=[/img], g(x) = 8 e h(x) = k, sendo x[img width=12,height=12]data:image/wmf;base64,R0lGODlhDwAPAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAIABQAJAAcAgwAAAAAAAB0AAAAcSB1IWzMzWzVIW2xGHW5GM39/XX9uSGaIiAECAwECAwECAwECAwQSEEgR6pA4y6IxrdbWYcQ4gVcEADs=[/img]IR e k uma constante real.[br][br] [br][br][img width=222,height=198]data:image/png;base64,/9j/4AAQSkZJRgABAQEAeAB4AAD/2wBDAAoHBwkHBgoJCAkLCwoMDxkQDw4ODx4WFxIZJCAmJSMgIyIoLTkwKCo2KyIjMkQyNjs9QEBAJjBGS0U+Sjk/QD3/2wBDAQsLCw8NDx0QEB09KSMpPT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT09PT3/wAARCAD3ARUDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD2aiiigAooooAKKKKACiiigAooooAKTNLXEa7p08njKLTYObLWQlxeANyn2cjPHo4Man6UAdD4p1xPDfhm/wBUk25t4iUB6M54UfiSKTwrrieJPDNhqiYzcRAyAdFccMPwINN8WWNte+Gr/wC1QpMIYJJYw4yFcI2Dj1Gan8P2NtY6Pbi0gjhEsayOI12gsVGTgdzigDSooooAKKKKAM3xFfvpfhvUr2I7ZLe2kkQ4zhgpI/Wq0msPpHg2LU9QDTTRWsbyquAXkIAx6DLGqnxEZh4Hv4kzvuPLgXHcvIq/1qXxno39reEriygtVuZQEMMbAcEMORnvjNPoV9k3LV5pLaN7iJYpmGWRX3hT6ZwM/lUtMhhjt4UhhRY4o1CqijAUDoAKfSJCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACq0WnWkF9Nex28a3U4CySgfMwHQZ9Ks0UAZ3iL/kWtU/69Jf/AEA1NpP/ACB7L/rgn/oIqHxF/wAi1qn/AF6S/wDoBqbSf+QPZf8AXBP/AEEUAW6KKKACiiigDl/HA86LRLTk/adWt1YDuqkuf/Qa6iuX8Qf6R418L22CVV7i5b/gMe0fq4rqKb2RT2QUUUUiQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAzvEX/Itap/16S/+gGptJ/5A9l/1wT/ANBFQ+Iv+Ra1T/r0l/8AQDU2k/8AIHsv+uCf+gigC3RRRQAUUUUAcu4+0fFKIYytppLN16NJKB/JDXUVy+if6R4+8S3HBEKW1sp/4AXP/oQ/KuopsqQUUUUiQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKrajcS2mmXVxBCZ5YYXkSIdXYAkL+J4rjtH8Q3s2seH42161v11KOSS4t44kBiIjLADHIAPHzc8fWgDuqKKKACiiigAooooAKKKKACiiuW1aO51Hxrb6cmpXtnbjT3nItXVSziRV5yD2NAPQ2PEX/ACLWqf8AXpL/AOgGptJ/5A9l/wBcE/8AQRXN/bbs6Z4p0m9uPtTafbny7gqFd0eIsAwHG4cjIAyMcV0mk/8AIHsv+uCf+gigC3RRRQAUUU2R1jjZ2OFUEk+1AHM+Cf38niC84Pn6tMFI7qgVB/6Ca6iuF0LU5dC+Ep1dYxJcGOW6CsOCzyMQT7fMPwre07QLu0ngup9c1C4nHM6uy+VLkcgJj5Bnpjn1zTluVPc3KKKKRIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAUrzUbe2YwytOrsvDRwO+M98hSM1zenWVpa6tFf3l9dXUsG7ysaY0WWYYLuVT52xkZ4HJ4rsaKtOHVP7/+AS1Lo/6+8zv7dsv+nn/wEl/+Jo/t2y/6ef8AwEl/+JrRop3p9n9//AFafdfd/wAEzv7dsv8Ap5/8BJf/AImj+3bL/p5/8BJf/ia0aKL0+z+//gBafdfd/wAEzv7dsv8Ap5/8BJf/AImj+3bL/p5/8BJf/ia0aKL0+z+//gBafdfd/wAEzv7dsv8Ap5/8BJf/AImj+3bL/p5/8BJf/ia0aKL0+z+//gBafdfd/wAEzv7dsv8Ap5/8BJf/AImsjUotP1DVI9Qjv9Ws7lITButrZhlCwbBDRt3ArqKKL0+z+/8A4AWn3X3f8E4bWdR0Xwv4L1do/t0jTxP5sssMhkmkcbAWdgB3A7AAcVf8MeNNJ1Lw3Y3EbzoDEEKtA5IK8HkAg8itfxJGkvhjVFkVWU2kuQwyPuGud0yNIdJs44kVEWCPCqMAfKO1VCMJPZ29f+AROUor+v8AM3/+Em0z/ntL/wCA8n/xNH/CTaZ/z2l/8B5P/iaysn1oyfWtPZ0+z+//AIBn7Wfl93/BNX/hJtM/57S/+A8n/wATWJ4y8caZpfhW+mR53lkiaGILC6/OwIByQAMdfwqbJ9awPGoE3h02pAY3dzBbgMM/ekH9AaHThbRP7/8AgFQqTcktP6+ZueGdV0i98C6batHcSWr2SQuj2sjBht2sDhSD3pbG1s7GeDGsa7La2xBhtpIpNgwMAEiMMwHoxPvmuqiijgiSKFFjjQBVRRgKB0AFPrG8Oz+//gGz531/D/gmd/btl/08/wDgJL/8TR/btl/08/8AgJL/APE1o0UXp9n9/wDwBWn3X3f8Ezv7dsv+nn/wEl/+Jo/t2y/6ef8AwEl/+JrRoovT7P7/APgBafdfd/wTO/t2y/6ef/ASX/4mj+3bL/p5/wDASX/4mtGii9Ps/v8A+AFp9193/BM7+3bL/p5/8BJf/iaP7dsv+nn/AMBJf/ia0aKL0+z+/wD4AWn3X3f8Ezv7dsv+nn/wEl/+Jo/t2y/6ef8AwEl/+JrRoovT7P7/APgBafdfd/wTO/t2y/6ef/ASX/4mj+3bL/p5/wDASX/4mtGii9Ps/v8A+AFp9193/BM7+3bL/p5/8BJf/iaP7dsv+nn/AMBJf/ia0aKL0+z+/wD4AWn3X3f8EhtrqO7i8yHftzj542Q/kwBoqaiodr6FrzCiiikAUUUUAFFFFABRRRQAUUUUAFFFFAGd4h/5FvVP+vSX/wBANc7Yf8g20/64R/8AoIrovEP/ACLeqf8AXpL/AOgGudsP+Qbaf9cI/wD0EVtS6mFboT0UUVsYBWFrv+keIfDln1zdtcsPaNcj9SK3aw4f9L+ITt1SwsVT6PI+f5LQaU97npFFFFcZ1BRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ3iH/kW9U/69Jf8A0A1zth/yDbT/AK4R/wDoIrovEP8AyLeqf9ekv/oBrnbD/kG2n/XCP/0EVtS6mFboT0UUVsYCgZIFYPhT/SrvV9SxxdX5RD6pHhB/WtPVb0abpF5eN/ywhZx9QOP1xVfwvYnTvDum2zDEgiVn/wB5vmP6mg0WkWzvqKKK4zqCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAzvEP8AyLeqf9ekv/oBrnbD/kG2n/XCP/0EV0XiH/kW9U/69Jf/AEA1zth/yDbT/rhH/wCgitqXUwrdCeiiitjAwPF3+lWljpS9dRu0jYf9M1O9/wBBXQrjzFxwMjFc8P8AiYePGPBi0q0x/wBtZf8A7EfrXQp99fqKDSWiSOqooorjOoKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDO8Q/wDIt6p/16S/+gGudsP+Qbaf9cI//QRXReIf+Rb1T/r0l/8AQDXO2H/INtP+uEf/AKCK2pdTCt0J6RnWNGeQ4RAWY+gHJpaw/F88n9iixtzi41KVbSPHYN94/goNbGUVzOw3wejy6XNqcoIl1O4e556hM4Qf98gfnXQJ99fqKiggjtoI4IRiOJAiD0AGBUqffX6igJPmlc6qiiiuM7AooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAM7xD/yLeqf9ekv/AKAa52w/5Btp/wBcI/8A0EV0XiH/AJFvVP8Ar0l/9ANc7Yf8g20/64R/+gitqXUwrdCesCP/AImvjeSTrb6PD5a+hnkHP5Lx+Na2p6hFpWmXN9P/AKu3jLkep7D8TgVS8MafLYaJH9q/4/Lljc3J7+Y/JH4DA/CtiI6Rcvka1OT76/UU2nJ99fqKDM6qiiiuM7gooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiioLS8gv7Zbi0lWWF8hXXocEg/qDQBPRRRQAUUUUAFFFFABRRRQAUUVHNcQ2yq08scSswRS7AAseABnuaAKXiH/kW9U/69Jf8A0A1zth/yDbT/AK4R/wDoIrovEP8AyLeqf9ekv/oBrllvIdO8Px3ly22GC1R3PsFFbUupjW1sZmtf8TjX7HRhzBBi9vPQqD+7Q/VufoK6InJzWJ4Xs5kspdRvl232pP8AaJQf4F/gT8F/nW1WxlP+VdApyffX6im05Pvr9RQQdVRVK81jTtOmSK+v7S2kcZVJplQsPYE1cBDAEEEHoRXGdwtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV594Tu7/T7bQQ16JbPULq5g+zeUoEYBlcMG6k5TnPHPtXa3baiJR9jjtGjx1ldgc/gDVUR6soQLa6WAhyuHf5T7fL7mp5rM0VFyV7r7zWorM363/wA8dO/7+v8A/E0b9b/546d/39f/AOJo5vIr2L7r70adFZm/W/8Anjp3/f1//iaN+t/88dO/7+v/APE0c3kHsX3X3o06KzN+t/8APHTv+/r/APxNG/W/+eOnf9/X/wDiaObyD2L7r70adFZm/W/+eOnf9/X/APiaN+t/88dO/wC/r/8AxNHN5B7F9196NOuC8Yb/ABHrb6TDZ3l3bWEBeRrUp+7unGIidzLyi5bjuy11W/W/+eOnf9/X/wDiaao1hCxW30xSxyxEjjJ9T8tLmD2L7r70ZkGrvrXw7u7mddl2tnNDdR945kUq6n8QfwxXIyf8VBe6fpC/NY2UMNxfHs7bQY4v6mtnx9q+raP4XuooItPS7vt0cccO53kyP3hC7R0TJJPSq/gjwxrdh4XthNHYpPPmaQvIxdi3QsQCM4x3raFRLVmcqLvZNX9Ta60lTf2PrH/UP/77f/Cj+x9Y/wCof/32/wDhV+2j/SMPqk+6+9ENOT76/UVJ/Y+sf9Q//vt/8KyvE2leLE0SVtEWyN6CNvlud+M87d4C5+tHtog8LNa3X3oZ4o58aXCfbNJtN2kKC+oxh1x5j9AWH9fpXReCpEl8GaSY4ZYUFsqqkpy2BwDnjIOMj2Iqpptrr11pVm+t2OkS36xjzGkJJDfgpAP04zWpv1v/AJ46d/39f/4mufmtpY6/ZN63X3mnRWZv1v8A546d/wB/X/8AiaN+t/8APHTv+/r/APxNHN5B7F9196NOiszfrf8Azx07/v6//wATRv1v/njp3/f1/wD4mjm8g9i+6+9GnRWZv1v/AJ46d/39f/4mjfrf/PHTv+/r/wDxNHN5B7F9196NOiszfrf/ADx07/v6/wD8TRv1v/njp3/f1/8A4mjm8g9i+6+9GnRWZv1v/njp3/f1/wD4mjfrf/PHTv8Av6//AMTRzeQexfdfejTorM363/zx07/v6/8A8TRv1v8A546d/wB/X/8AiaObyD2L7r70adFZm/W/+eOnf9/X/wDiaN+t/wDPHTv+/r//ABNHN5B7F9196NOiobU3Jh/0xYVlz0iYlcfiBRVGTVnYmooooEFFFFABRRRQAUUUUAFFFYeqeMdF0mXyJrwTXZ+7a2wMsrH02rk/nii1xpN7G5WHr3ii30d0tIInvtVmH7ixgOXb3b+6vqxrP87xR4j+WGIeH7BuskuJLtx7L91Pxya19E8OafoETiyiYzSnM1xKxeWY+rMeT/KnZLcdktzDk0C4h0fV9Y1yVLjWJrGVfk/1dsmw/u4x6ep6mum0n/kD2X/XBP8A0EVD4i/5FrVP+vSX/wBANTaT/wAgey/64J/6CKQm7luiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZeoeJtF0q6+zahqlnbT7Q3lyyhWwehwarf8Jv4a/wCg7p3/AIEL/jWtNZWtw++e2hkbGMugJ/WoX0bTZMb9PtGx0zAp/pTVily9TP8A+E38Nf8AQd07/wACF/xpjePPC6Ak67p/HpMDWomj6dGMJp9ooPpCo/pUq2VqgwltCo9kAo0D3Tm5fid4RiB3a3Acf3Vdv5CqLfGDwsXCW09zcse0cJH/AKFiuz+y2/8Azwi/74FBtLc9YIv++BRoK67HFH4l/aADY6XHgjhrvUreAfluJ/SkPiXWL7rr3hTS4z/duftMg/Mqtdr9itf+faH/AL9ij7Fa/wDPtD/37FF/IfN5HE/YNEvude8bHUgfvRC/jt4T/wAAjI/nW1pd34Q0WIx6ZeaLaqevlTxgn6nOT+Nbn2K1/wCfaH/v2KPsVr/z7Q/9+xRdicmyl/wk+hf9BrTf/AqP/Gj/AISfQv8AoNab/wCBUf8AjV37Fa/8+0P/AH7FH2K1/wCfaH/v2KQjD17xJosvh7Ukj1jTmdrWUKq3SEk7DwOal0zxLoiaVZq2s6crLAgIN0mQdo96n8QWdsvhvUyLeEEWkuCEH9w1NpVnbHSLMm3hJMCfwD+6KAGf8JPoX/Qa03/wKj/xo/4SfQv+g1pv/gVH/jV37Fa/8+0P/fsUfYrX/n2h/wC/YoApf8JPoX/Qa03/AMCo/wDGj/hJ9C/6DWm/+BUf+NXfsVr/AM+0P/fsUfYrX/n2h/79igCl/wAJPoX/AEGtN/8AAqP/ABo/4SfQv+g1pv8A4FR/41d+xWv/AD7Q/wDfsUfYrX/n2h/79igCl/wk+hf9BrTf/AqP/Gj/AISfQv8AoNab/wCBUf8AjV37Fa/8+0P/AH7FH2K1/wCfaH/v2KAKX/CT6F/0GtN/8Co/8aP+En0L/oNab/4FR/41d+xWv/PtD/37FH2K1/59of8Av2KAKX/CT6F/0GtN/wDAqP8Axo/4SfQv+g1pv/gVH/jV37Fa/wDPtD/37FH2K1/59of+/YoApf8ACT6F/wBBrTf/AAKj/wAaP+En0L/oNab/AOBUf+NXfsVr/wA+0P8A37FH2K1/59of+/YoApf8JPoX/Qa03/wKj/xo/wCEn0L/AKDWm/8AgVH/AI1d+xWv/PtD/wB+xR9itf8An2h/79igCl/wk+hf9BrTf/AqP/Gj/hJ9C/6DWm/+BUf+NXfsVr/z7Q/9+xR9itf+faH/AL9igCl/wk+hf9BrTf8AwKj/AMaytU+I3h7R723hur6JoZwdtxA6yojDs20kjr1xjr6Vqapd6XoywSX0EcUEsnlmYxDy4zjjef4QcYz0yRVIaBoXif7Fq1zpvmKqEwRXEe1VBP3jH0ycDr2x0oA27K+ttRtI7qynjuLeQZSSNgyn8RRUscaRRrHGioijAVRgD8KKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBneIv8AkWtU/wCvSX/0A1NpP/IHsv8Argn/AKCKh8Rf8i1qn/XpL/6Aam0n/kD2X/XBP/QRQBbooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDL1vQ4tejht7yRjYq26e2A4n/uhj1wDzgdSBVjSrKTTtOitJbqS6MQ2rLKBvK/wgkdSBgZ74zVyigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6xbSXmi31tCAZZreSNATgZKkD+dSWEL2+nW0MgAeOJVYA9wADRRQBYooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAP/2Q==[/img][br][br] [br][br]No retângulo[br]ABCD, destacado no plano, os vértices A e C são as interseções dos gráficos [img width=31,height=15]data:image/wmf;base64,R0lGODlhJwATAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAIABQAhAAsAhQAAAAAAAB0AAB0dAAAAHR0AHQAdMgAcSB4zRx0zWgAzWh1GbDMAADMeRzVbbjNbgEgcAEceM1ozAFozHUczHkhbSEhbbkhuf1luf11/f2xGHW5bNX9/XX9uSH9uWWaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwZkQIBQEggIj8ikkvFQAiTHg3N6ZBidTKr2KGgqBdtB0TAFK4sBwsWJSCaSHYEDcOVSF048UkAQ9rleSQ1bgEIFa0JmhEcaSYqKcYFIkkl6AJGXXXaLRyCOm3RFTpRIllZ9AmkAQQA7[/img] e [img width=29,height=17]data:image/wmf;base64,R0lGODlhJAAVAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABAAeAA4AhQAAAAAAAAAAHR0AABwcHB0AHQAAMwAcSB0dSAAzWh0zWh1GbDMAADQdHTMeRzVIWzNGbjNbgEgcAEgdHVozAFozHUZGbkhuf11/f2xGHW5bNW5GM39/XX9uSH9uWWaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwZjQICQEhAIj8ikcrkASJbQqJAhrUIZEasWAAp4DcvKoKhYjr2HI3bZSBKSVGECGU9Olghk4ZhWZ5EdUX9OR3NqW2YBYHSDQhtREEcOiQGGiE5eXpdRFkeBm0oUlgCNoFOZTQBBADs=[/img], respectivamente.[br][br]Determine a área desse retângulo.[br][br]
Questão-02 - (UEL PR/2012)
[br][br]A espessura da camada de creme formada sobre um café[br]expresso na xícara, servido na cafeteria A, no decorrer do tempo, é descrita pela função [i]E[/i]([i]t[/i]) = [i]a[/i]2[sup]bt[/sup], onde [i]t[/i] [math]\ge[/math]0 é o tempo (em segundos) e [i]a[/i] e [i]b[/i] são números reais. Sabendo que inicialmente a espessura do creme é de 6 milímetros e que, depois de 5 segundos, se reduziu em 50%, qual a espessura depois de 10 segundos?[br][br]Apresente os cálculos realizados na resolução da questão.
Questão-03 - (UFU MG/2018/Julho)
[br][br]O setor de controle de qualidade de um frigorífico avalia o[br]funcionamento de algumas de suas câmaras de refrigeração. Um boi foi abatido e[br]parte de seu corpo foi colocado em uma câmara, mantida a uma temperatura[br]constante de –10º C, para resfriamento. Nela, instalou-se um termômetro para[br]aferir a oscilação na temperatura desse corpo.[br][br]Considere que a temperatura do corpo, em graus Celsius, varie com o[br]tempo t, em minutos, de acordo com a função [img width=95,height=20]data:image/wmf;base64,R0lGODlhdwAZAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABQBvABAAhQAAAAAAAB0AHQAAHR0AAAAAMx0AMgAcSB0dSAAzWh0zWh1JSR1GbDMAADIAHTIAMjMeRzMzWzNbgEgcAEgdHVozHVozAFtIHUhIW0ZGbkhuf11/f2xGHW5GRn9/XX9uSGpqamaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwb/QIBwSCwaj8ikcslsLhnOqHRKrSobR0w0UaxYv2DqolEYigLcgHodKB6Ok7DxIzC25UqO2lwGcIUKABxDBkNQQghJDnhDAQNEFlAcf4xMh0kfhUUWRRJFlHgOGkOLQqWVRJ5EIoZDgUSaRA9DBGpvhKinrENxU2tLEwF9jWhEDZQfR7dCDaq8qG7PSM5EdULLSo9SsUIc2FhFE5cAwWzFvObnAKfevONS2EqgS5lG39TkuaPX0ujmRw0CfHtnhRu/IeCI9PLHZp6SUwBiQWwyoU+8JBGi0DECsVmRWdCGcBLicAg+IcMuHvHixMIagiIFhhRS646QYCqXBFyTE0BNFzz1kuybSbQoABEqFxpdylTIyaZQkQQBADs=[/img], em que a e b são constantes reais e t, o tempo decorrido após o corpo ser colocado na câmara de refrigeração. Assim, após 80 minutos,[br]foi observado que a temperatura do corpo era de 0ºC e que, após 2 horas e 40[br]minutos, essa temperatura passou para –8ºC.[br][br]Levando-se em consideração essas informações, elabore e execute um plano de resolução de[br]maneira a determinar[br][br][br]a)     os valores das constantes reais a e b.[br][br]b)     o instante de tempo t, em horas, a partir do qual [img width=72,height=17]data:image/wmf;base64,R0lGODlhWgAVAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABABUAA4AhQAAAAAAAB0AAAAAHR0AHQAAMx0AMh0dNAAdMgAcSB0dSAAzWh0zWh4zRx1IWx1GbDIAHTIdADMAADQdHTIAMjQ0NDNdXTNbgEgcAEgdHVozHVozAFszM0ZGbkhuf11/f1luf2xGHW5bNW5GM25bSG5GRn9uSH9/XW5uWX9uWW5ugGaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwb5QIBwSBSyikINcslsOp9QQGBKDQyPTEzUEQUIAgWnSTAAjMvIzRQNCA0Nw0cU4owwuvR2ghliD/dEEoAAGH4mcEUXiUULSxFdf0MSSyxhQxlLWkgeRIhDFERfAYMAnkITB5BCbkMYckUYFVNCG3IKoa9MJkVYgYpEmkOPqkICrUuWAGVnRVZPpgCkAJOwucINmVWzQlVIIYPU3s5Nh0SsvrBNw8TSQoPBSONN0NLhx8ROxkiV95ntRCYIbEJHBBQ+JvLSuSMnYFAvAGqm5NpQRM2/VdoSNiFTUZ4EMFA+TmkEBdrAgyhTPrkITyWfZC6j3EHyK6bNJ0EAADs=[/img].
Questão-04 - (UFG GO/2011/2ª Fase)
[br][br]Quando um[br]antibiótico é ingerido, é absorvido pelo organismo e eliminado gradativamente.[br]Denotando por q[sub]0 [/sub]a quantidade do antibiótico no organismo do paciente num instante t[sub]0[/sub], a função[br]que descreve a quantidade, em um instante posterior t, com t – t[sub]0[/sub] em horas, enquanto não houver nova ingestão do antibiótico, é q(t) = 2[sup]–(t–t0)/2[/sup] q[sub]0[/sub] [br][br]Havendo ingestão de antibiótico, soma-se a quantidade ingerida à quantidade já presente[br]no organismo e, a partir daí, a quantidade decresce com o tempo segundo a função acima.[br][br]Considere o tratamento de uma infecção com cápsulas de 500 mg desse antibiótico, ingeridas[br]em intervalos regulares, sendo uma cápsula a cada x horas.[br][br]Para conveniência do paciente, x deve ser um número par de horas e, para que o tratamento seja eficaz, a[br]quantidade de antibiótico no organismo do paciente deve ficar acima de 60 mg durante todo o tratamento. Nestas condições,[br][br]a)     que quantidade do antibiótico da primeira cápsula, em mg, restará no organismo duas horas após[br]sua ingestão?[br][br]b)     Qual é o maior número par x (intervalo entre as cápsulas) para que o tratamento seja eficaz?[br][br]
Questão 5
[br][br]Uma indústria consegue produzir em t dias de trabalho [img width=66,height=19]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFMAAAAYCAMAAACx8zGdAAAAAXNSR0IArs4c6QAAAIRQTFRFAAAAAAAAAAA6AABmADo6ADpmADqQAGa2OgAAOgA6OgBmOjoAOjo6OjqQOmaQOma2OpC2OpDbZgAAZgA6ZjoAZjqQZma2Zrb/kDoAkGYAkGY6kLbbkNv/tmYAtmY6tpBmttv/tv//25A627Zm27aQ29u22////7Zm/9uQ/9u2//+2///bPbjY3AAAAAF0Uk5TAEDm2GYAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAAZdEVYdFNvZnR3YXJlAE1pY3Jvc29mdCBPZmZpY2V/7TVxAAABdklEQVRIS+1UW1vDIAwl02q9Ta2X4jq2SVVo+f//TxIuHWvLN+ej5mUrJCcnJwmM/dsvFfh8BrhHDHU5gWS2d+/+WC53R6bqnxrWLtaMGf44DjH84Sue6tv6SFDrpq/WrK8AAFGV/QU4bzD8IA/6Zcy0NwCFd5GIpa99kdKyNm9Inakzdxaw5cXAegwuFg3rOAWy1skZ/CUCKbB1Gu4lbvHLFzRPVKC3JFdJkEx4OQ1HcMLUJUEZjmpgwKTmaRJBjCykqq173b1iZX2F4O7K1WG/Qg1EJWPdCoeDeoOkNlCQeMjQbFy7PGbUYABnglqJFhI7rOWU4hL9Cmo7KRupJ4TnuH6UPiZxiHUOPKMGezznQBVVmFpfDZIFrMDXChsvp2pHJF2OMX2vKVH4H6m7/s2YGwoamAMTe2ehN3YIuheUNrtIBse9o0lMzXZo6GPYI11CsaOmZfeoW5X2OcptGmL8bN/nZUluTn+XMglOej+PJPwH3L4BV6cdzce5sEIAAAAASUVORK5CYII=[/img] produtos no período da[br]manhã. No período da tarde, para o mesmo número de horas, em t dias a produção[br]é  [img width=117,height=18]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJIAAAAXCAMAAADX2ObXAAAAAXNSR0IArs4c6QAAAJBQTFRFAAAAAAAAAAA6AABmADpmADqQAGa2OgAAOgA6OgBmOjoAOjo6OjpmOjqQOmaQOma2OpC2OpDbZgAAZgA6ZjoAZjo6ZjqQZmZmZma2ZpDbZrbbZrb/kDoAkDo6kGY6kLbbkNv/tmYAtmY6tpBmttv/tv//25A625Bm27Zm27aQ2////7Zm/9uQ/9u2//+2///b+vcTwgAAAAF0Uk5TAEDm2GYAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAAZdEVYdFNvZnR3YXJlAE1pY3Jvc29mdCBPZmZpY2V/7TVxAAACLUlEQVRIS+1Wa1fDIAwtdYpvXX1vdYqPukkp///fSQJJYaXb8Wwfx5edtUm4ufcSWhSHdWBghAF9siM19vPqO5Rorr92LAbptp7uVsXWt79cob2Y/6vaz/swvKuEEFtADfPMQojyBauttdSeZjbpt7WreyEmENJKt7Eo+2i7PKdXZ8R6pr00r6ECrTz+Kpa+E33k8wlac9xzNqyoxKwwFaS0co1PVb4VpoYtdFrC1nFkktfKAKmrwH62hkxbBysuhU/cTJOC6AZCh5D4lUpVG4fUVU8BkvK/KmrW1iCDR7rVmzoLCRuCmg6CeY6oHoekptpDaaUnBiGFZ+4fsY1EbFxxL0mgWeCJ/RCT2EyjkPTVb9gemyThCBIL2GMrFDCHK3IxSdbKS+mNTgtO2nXGiOuQKK+7eydGsEmoDAo1wd1dRXoxXSNMBWXtqzM6ujlaKxnK0bNhV5yHdRwjzTzYOpiUhWMBI5aymHo6ua0oTmcGUsoSBgMdmiRgSF2F5iEoxJYzFXspK5w6ibTxZzdanvp0ZSBxXtjeCxeGFJ1llqtXMEsSji3t9sWTHiHwegafJqkppDSP7T0t7Ec5wzzSweE0jwB181zCtxbKwiQxtesudGzBVwZn3UaWOA+jaHov3V3A92uY3m7OT/DK3Ta90QEOknlwv1CFRDALV/Zm64njPNjM+YkOSMTv/+64rJh7eQjeXvlr10m3w5fAXtD4Ilr2HO/9e2mPOA+lmIE/40Y6+glLc3cAAAAASUVORK5CYII=[/img] produtos. Em quantos dias a produção matutina será a mesma que a vespertina?[br][br][br][br]a) 3 dias[br][br][br]b) 4 dias[br][br][br]c) 5 dias[br][br][br]d) 6 dias[br][br][br]e) 7 dias[br][br][br][br]
Questão 6
[br]Pesquisadores descobriram que o crescimento da população de bactérias que produzem substâncias antimicrobianas obedece a função [img width=111,height=31]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAIsAAAAnCAMAAAAIGUtYAAAAAXNSR0IArs4c6QAAAKtQTFRFAAAAAAAAAAA6AABmADo6ADpmADqQAGa2OgAAOgA6OgBmOjoAOjo6OjpmOjqQOmaQOma2OpC2OpDbZgAAZgA6ZjoAZjo6ZjpmZjqQZma2ZpDbZrbbZrb/kDoAkDo6kGYAkGY6kGZmkGaQkLaQkLbbkNv/tmYAtmY6tpBmtrbbttv/tv//25A625Bm27Zm27aQ27a229uQ29v/2////7Zm/9uQ/9u2//+2///bOc4IqwAAAAF0Uk5TAEDm2GYAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAAZdEVYdFNvZnR3YXJlAE1pY3Jvc29mdCBPZmZpY2V/7TVxAAAC+0lEQVRYR+1X23abMBBESZyozY2W3h2ctE1w2+C4rQXo/7+suyutLj7C9JzG4IfqxQKL3dHs7Aiy7P84YAbU2cGA0+XrQ8HSFUKIQ0HTvHycgpf28w9Oq/KNnapTno0Jqbl48OnqS0tHNUWBuuIGoKzOxdEnhFQbPnR5034cnZkKe1cv7rOnI+SH+2cpZqMLpnnBFbIzdTw6BpYI0YKjvZvT73TG0khUC4xKnBgsWb2LGP3timmrr137PU+rBYnXFpaDl8igy1de0M2F3cdfQlkF/Zp6pDJt0715yBhDV0TtrMCAhTi5T9TPay2JRq/fCjFDAI3EGNQbIIKlpKT6ToirgNqusHJZSdvTKJjY5mqIoW8pEOuaNWUNoIeXSsyztsCKh1Qrmf82+zrdtGWgh0YmLK2KBUNlVALqoUuL/AmvcL+uCZOc4+oalwZYlLSyVLg7CmtHOHc3kQg/DE200IbUJTJOtjR8mIcPohi4EBnt2F/GuHqwGPnQk7QVHFZlMBl8yaEHPS9u82aLXeH1EFNg0RCtEXV6Se8PjMXVyoMCT+ARsWpQNPJSGhVXx19B0HACGyyhNpNY4sLVmGNGbcQG4DvNEdQjX1tEvQAVl9gDpQBTWINK+7HwnihkjCVIx7y4WgW8JMF4AokcRoCPcY18kYe1G6nL0u8N0uslWaPqLDjqMZKtCQaw2vV9PIwltAaeO6q2bHGbG7IfBdnoZYj8w/gFBiBVhvmTfh/5SxUImSmHBe0HjLnbX+hfjTgqINT4WiOBKrInbCGiiZlPe13gu6DcoC+s74Klz8i8h3yXZAhY2nfwa47SBs8F6oQWZtfU10Yzkbgsxal77q/IpgfOo57e6r2daMokVw7MP5zTQ9h8e3pzi8xqK8A+3198J/i3qkm+RkL56cW5cX7zXTDJ4NT1vDQYdvfGfjGa3CqHL6KJaYH06OPd+0ddzr/g8TnF96JjWy/yDR3GAoxwke+3CoPRf6KfU43a74OLx1jwS073wTjG/p41xx/9uFdO0IDi1gAAAABJRU5ErkJggg==[/img], onde t representa o tempo de horas e P a população total. Para obter uma população de 810 bactérias, serão necessárias:[br][br]a) 2 h[br][br]b) 3 h[br][br]c) 4 h[br][br]d) 27 h[br][br]e) 64 h[br][br]
Questão 7
[br][br]Com relação a equação [img width=125,height=18]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJwAAAAXCAMAAADJEdZkAAAAAXNSR0IArs4c6QAAAJ9QTFRFAAAAAAAAAAA6AABmADo6ADpmADqQAGa2OgAAOgA6OgBmOjoAOjpmOjqQOmaQOma2OpDbZgAAZgA6ZjoAZjo6ZjpmZmZmZma2ZpDbZrbbZrb/kDoAkDo6kGY6kJC2kLaQkLbbkNv/tmYAtpA6tpC2trZmttuQttu2ttv/tv//25A625Bm27Zm27aQ2//b2////7Zm/9uQ/9u2//+2///bYi5UgQAAAAF0Uk5TAEDm2GYAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAAZdEVYdFNvZnR3YXJlAE1pY3Jvc29mdCBPZmZpY2V/7TVxAAAB9UlEQVRIS+2V2VbCMBCGExGIG1KLa0UhblCodMn7P5uTpE2zTHE5Hr1pLnqa7e+Xf2ZSQvrWO/B/DuRsTHI2/THAZklg/+9qZDGlwxUh4rk4fr3e3nXBie0JLAQAq2Uz1S8YhXaw/FSj3prCUt2E+rrsoRrpwYIIPljLlcnYJROJhcphYZkYWVhZxlTtA2GzLtBAzlowo8LpLSkjqYJpVJGMY/2MvZi6cJI8pS1uMVmlAVzla4RwVXTVwhlRC85o6DGRjHabt8uX0fuDLebAqQltsWk+HKIRwvFpbvsPiSpPbOAsDe2ZhOPDdRW7OeXDlfMJJOceOEQjgMvPdh6cOrGBszX4APL4iY52SHK4cFVE6cRdZpw7ZX6taKNloahmvKoulsSF01gFQzTEHMrlMfJKAdUlJGNoWMU9pLVTK8hJ9ZBIIFIAl1olpDK9W6PAr7cw53KqlJpWO6e6HRoeZt5Y2cA55Y1qtBePoxXCebttuCp0Hwur/IAdVj62MgXTwMZ0DNqLQ8VDF1bgHJdTX3NO7bXgUpnsOezv0sjYOVYOPhzkdAlVLW/FJkNrx7mactPRC6fTVduUSnEEb0KC4RpQJosOJSes5Rx+UuoUNZyQA/TwBn4VM3jxbpk9cJB3QKdU6nIGuG9q7Dt7P9c70Dvw1w58AO/bOX/QALQrAAAAAElFTkSuQmCC[/img], é correto afirmar que:[br][br]a) não tem raiz real.[br][br]b) tem uma única raiz real.[br][br]c) tem duas raízes reais.[br][br]d) tem infinitas raízes reais.[br][br]e) tem apenas raízes irracionais.[br][br]
– Felipe Morais Peixoto

8.

Questões sobre função exponencial.

  • 1. Questões de nível fácil.
  • 2. Questões de nível médio.

8.1.

Questões de nível fácil.

Questão-01 - (Famema SP/2024)
[br][br]Seja f:IR[img width=18,height=14]data:image/wmf;base64,R0lGODlhFgARAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABQAPAAcAgwAAAAAAAAAdMh0zWh1GbDNGbjNbgEgcAFozHUhbbkhuf2aIiIBbM4iIZgECAwECAwQYEMg5Gb0YDczBoUEojmJHHUJiStoqWVQEADs=[/img]IR uma função exponencial, dada por [img width=80,height=24]data:image/wmf;base64,R0lGODlhZAAeAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABABeABUAhQAAAAAAAAAAHR0AAB0dAAAAMx0AMgAcSAAzWh0zWh1GbDMAADIAHTIAMjMeRzNGRjNGbjVbbjNbgEgcAEgdHUceM1ozAFozHUYzRkhIW1tISEhZf0ZGbll/WUhuW11/f0huf1luf2xGHW5GM25bNX9ZSG5dXX9uSH9uWX9/XWaIiIBbM4iIZgECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwECAwb/QIBwSCwaj8ikcjmcBArMoiggiFqvWOwhK0Rwv+DrycDEFFfhtBrZEDoBg7VwEx3JwaeoeTgIGKlEe3pccXdEUE0BiopeQltDCgATQ2hYEmJ9VyuKR5dEBEeCRwtrCVmFWKRKphRRkUILnkNtWLRXqlmPAItVkkIDukKCjEOLiEJkRE5VC71EDFmqTsFKjYYAsUXUXQAXR5OpQyBXsoa4QpVGC37fsk6LxESkE69Rptew5QDbv/pu0U9GHamAb8g5R0mOKVMGj1MRVdaUeCuYr0iyIxaOtAqHrR4SEZTw9QkQ0ZYbdn2omWSyzo+FgEheGqNoZOKVezRzJvG4xI7ODZ9AgwodStRInqJEgwAAOw==[/img], com k sendo uma constante real. Um esboço do gráfico dessa[br]função no plano cartesiano de eixos ortogonais está representado a seguir.[br][br] [br][br][img width=185,height=124]data:image/png;base64,/9j/4AAQSkZJRgABAQEAeAB4AAD/2wBDAAoHBwkHBgoJCAkLCwoMDxkQDw4ODx4WFxIZJCAmJSMgIyIoLTkwKCo2KyIjMkQyNjs9QEBAJjBGS0U+Sjk/QD3/wAALCACbAOcBAREA/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/9oACAEBAAA/APZqKKKKKKKKKK53WfEkum6/BZLEFtktpLu6meJ2wi44UjgHryfYd6fH4qtbSyibWXFrdPbrcmIIxyrHAVePmYEqCBzk9OauWOqPNrN7p1wipJCqTQkAjfE+RyPUMrA/hVdvFdgvjBfDhf8A0xrfz8546/d+uOfpW3RRRRRRRRRRRRRRRRRRRRRRRRWFrugSas906Sqol06a0Cn+85BBz6cVmXWhX/iWLTtQedbOexiWS2iaLJjuRw5f1XjbgdiT6VpWcM8/ii/1BoyFhto7SMEECRwS7EE9ssoz7GvKX8AeNJPHj6uJ7AaksgvP9cdoBYgL93pgY+le5RljGpkUK5A3KDnB+tOoooooooooooooooooooooooooorLT/ka5f+vJP/Q2rUooooooooooooooooooooooooooorLT/ka5f+vJP/Q2rUooooorOsZJJ9X1Fy7GGIxwovYELuYj/vsD8K0aKKKKKKKKKKKKKKKKKKKKy0/5GuX/AK8k/wDQ2rUoooopskixRtJIQqICzE9gKz9AjI0pJnXbJdM1w/1c5H5AgfhWlRRRRRRRRRRRRRRRRRRRRWWn/I1y/wDXkn/obVqUUUUVl6+xk09bNGIe9kW3BHUKeXP/AHyGrTUBVCqAABgAUtFFFFFFFFFFFFFFFFFFFFZaf8jXL/15J/6G1alFFFFZQ/0zxIT1jsIsf9tJP8FA/wC+61aKKKKKKKKKKKKKKKKKKKKKy0/5GuX/AK8k/wDQ2rUoooqOaZLeCSaVtscalmJ7ADJqjoUTrpwnmUrPdubiQHsW6D8FwPwrSooooooooooooooooooooorLT/ka5f8AryT/ANDatSiiisrWv9Le20xeRcvum9olwW/M7V/4FWrRRRRRRRRRRRRRRRRRRRRRRWWn/I1y/wDXkn/obVqUUUhOBk9KytHzezXGqt0uCEt89oV6H/gRy30IrWoooooooooooooooooooooorLT/AJGuX/ryT/0Nq1KKKytXdruSPSYSd1wN07A/ch/i/Fvuj6k9q00RY0VEUKqjAA6AU6iiiiiiiiiiiiiiiiiiiiiistP+Rrl/68k/9DatSiquoX8enWjTSBnOQqRoMtI56KB6modKsZLaOSe7Kte3J3zMvQeiL/sqOPzPetCiiiiiiiiiiiiiiiiiiiiiikByMjpWYn/I1y/9eSf+htWpVe9vYdPtjNcNhQcAAZZmPRQO5PpVLT7S4ubkajqahJsEQW+ci3U+p7ue57dB3J1aKKKKKKKKKKKKKKKKKKKKKKyPE6ae+iSHV5pI7JHR5FjYgy4IxHgcsGOBtHXpXKhb3SdHlt0truxg1W5eQR28bSmwg2jI+XO12x0HALH0q/4FmWe209kEgC6VEn7xSDw7Dvyfr3roLnWFEzW2nxm8u14ZEOEjP+23Rfpyfaiz0tluRe6hKLm8wQpAwkIPZF7e56n9K0qKKKKKKKKKKKKKKKKKKKKKKZLNHCm6WREX1Y4FYurXXh/V4BZ3wh1FA+fJRDN8w9lB55qLS7ZNNtng8P8Ah9bOGU7mMxEKk46lRlvTsKrWuiu2um2u5wkEdigW3swYowu9gFJzuI/EfSumt7aG0hWG2iSKJeiIuAKloooooooooooooooqvNfWlv8A665gj/35AP51Xl1/SoCBJqFsCegEgJP5U06/YlwiNPIx6eXbyMPzC4pBrJeRkj03UGI7mEID+LEUn2/U3TMWjspz0muUX/0HdS7tadxhLCJMc5Z3I/QUhsdVkA8zVljOcnyLZRx6fMWpf7EWQt9ov9QmDdV88oPw2Yp0egaXG5f7DC7tjLSDeTj3bNX1RUUKihVHQAYp1Zaf8jXL/wBeSf8AobVqUUUUUUUUUUUUUVUvrNLwRh7i4h2HP7mUpu+uOtVpNDsJsedJcyY9buT+jUNoOkOAJLSCXHTzPn/nmpl0zTFAC2doAOn7peP0q0gijGE2KPRcCnb1/vL+dG9f7y/nRvX+8v50b1/vL+dG9f7y/nRvX+8v50b1/vL+dG9f7y/nRvX+8v51lo6/8JXL8w/48k7/AO21am9f7y/nRvX+8v50b1/vL+dG9f7y/nRvX+8v50b1/vL+dG9f7y/nRvX+8v50b1/vL+dG9f7y/nRvX+8v51x158UNG0rxZdaHqpe1aErsuT80bblDc45Xr9K663uYbuBZraaOaJxlXjYMpHsRUtV7rT7S+2/a7WCfZnb5sYbH0zVf+wdJ/wCgXY/+A6f4Uf2DpP8A0C7H/wAB0/wo/sHSf+gXY/8AgOn+FH9g6T/0C7H/AMB0/wAKP7B0n/oF2P8A4Dp/hR/YOk/9Aux/8B0/wo/sHSf+gXY/+A6f4Uf2DpP/AEC7H/wHT/Cj+wdJ/wCgXY/+A6f4Uf2DpP8A0C7H/wAB0/wo/sHSf+gXY/8AgOn+FH9g6T/0C7H/AMB0/wAKzNattO037LDaaFYXV5dy+VDE0aIvClmZm2nAAB7HtVHQ7bTNW1iWSTRrO3eO38qWAxIwjkWV1bkDB6cHuMV0P9g6T/0C7H/wHT/Cj+wdJ/6Bdj/4Dp/hR/YOk/8AQLsf/AdP8KP7B0n/AKBdj/4Dp/hR/YOk/wDQLsf/AAHT/Cj+wdJ/6Bdj/wCA6f4Uf2DpP/QLsf8AwHT/AAo/sHSf+gXY/wDgOn+FH9g6T/0C7H/wHT/Cj+wdJ/6Bdj/4Dp/hR/YOk/8AQLsf/AdP8K4bUfg7Y614wu9UvphFYOU8q0tV2ZwoBye3IPT867SyttH8L29rp1pHBZRTOUhjHG98ZPPc4B6+lXrK9t9RtEubOVZoJM7JF6Ng44/Kp6KKKKKKKKKKKKxtfsL2ebT77TVhkurGYuIpmKrIjKVYbgDg85HB6VR8Oafc6frNwb0R/armE3E3lElFZ5XO0E9cDAzXT0UUUUUUUUUUVheLNDm8SadHpiskVrNIDcTf8tEVeRs/2icc9hmr+jQ3dvpFtBfrAtxEgjb7P9wgcAgdsgDjt0q9RRRRRRRRRRRRRRRRRRRRRRRRRRRRX//Z[/img][br][br] [br][br]Sabendo que 24 representa o intersecto do gráfico de f (x)[br]com o eixo das ordenadas, o valor de k é igual a[br][br] [br][br]
Questão-02 - (ENEM MEC/2023/1ª Aplicação)
[br][br]Um agricultor é informado sobre um método de[br]proteção para sua lavoura que consiste em inserir larvas específicas, de rápida[br]reprodução. A reprodução dessas larvas faz com que sua população multiplique-se[br]por 10 a cada 3 dias e, para evitar eventuais desequilíbrios, é possível cessar[br]essa reprodução aplicando-se um produto X. O agricultor decide iniciar esse[br]método com 100 larvas e dispõe de 5 litros do produto X, cuja aplicação[br]recomendada é de exatamente 1 litro para cada população de 200 000 larvas. A[br]quantidade total do produto X de que ele dispõe deverá ser aplicada de uma[br]única vez.[br][br][br]Quantos dias após iniciado esse método o agricultor[br]deverá aplicar o produto X?[br][br] [br][br]
Questão-03 - (ENEM MEC/2023/2ª Aplicação)
[br][br]Um[br]tipo de célula se reproduz constantemente por divisão celular, triplicando sua[br]quantidade a cada duas horas, sob condições ideais de proliferação. Suponha uma[br]quantidade inicial [i]Q[/i][sub]0[/sub] dessas células sob as condições ideais[br]de proliferação durante um certo período.[br][br] [br][br]Qual a[br]representação algébrica da quantidade [i]Q [/i]dessas células em função do[br]tempo [i]t[/i], em hora, nesse período?[br][br] [br][br]
Questão-04 - (UEMA/2021)
[br][br]Numa[br]concessionária de caminhões zero, o vendedor informou ao comprador que a lei[br]matemática que permite estimar a depreciação do veículo comprado é v (t) =[br]65000[img width=6,height=10]data:image/wmf;base64,R0lGODlhCAAMAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAIABQADAAEAgQAAAB1GbDMAAH9/XQIChFAAOw==[/img]4[sup]–0,04t[/sup], em que v([i]t[/i]) é o valor, em reais,[br]do caminhão, [i]t [/i]anos após a aquisição como zero na concessionária.[br][br] [br][br]Segundo[br]a lei da depreciação indicada, o caminhão valerá um oitavo do valor de[br]aquisição com [br][br]
Questão-05 - (PUC RS/2021/Janeiro)
[br][br]Em novembro de 2019, foi diagnosticado, na China, o primeiro caso da infecção[br]conhecida por COVID-19. No Brasil, os primeiros casos surgiram no final da[br]segunda quinzena de fevereiro de 2020. No dia 23/03/2020, foram diagnosticados,[br]no Brasil, 1.960 casos. Supondo que a evolução prevista para o nú­mero de[br]pessoas infectadas pelo novo coronavírus é dada por P = 1.960 [img width=7,height=10]data:image/wmf;base64,R0lGODlhCQAMAHcAMSH+GlNvZnR3YXJlOiBNaWNyb3NvZnQgT2ZmaWNlACH5BAEAAAAALAMABQADAAEAgQAAAB1GbDMAAH9/XQIChFAAOw==[/img]2[sup]t/5[/sup], em que [i]t [/i]é o número de dias corridos,[br]a partir do dia 23/03/2020, e [i]P [/i]o total de pessoas infectadas, quantos[br]dias são previstos para que o número de pessoas infectadas seja 15.680?[br][br]
– Felipe Morais Peixoto

8.2.

–

Información