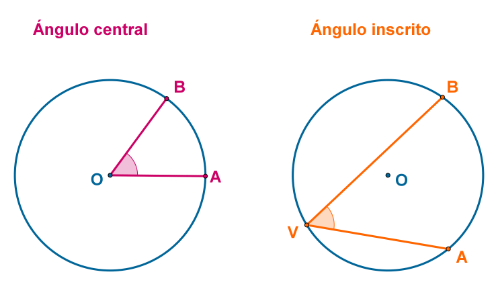
Dos tipos de ángulos que existen en los círculos son los ángulos centrales y los ángulos inscritos.

Un [b]ángulo central[/b] es el ángulo formado entre dos radios como sus lados y el centro del círculo como su vértice. Veamos el ángulo central en la siguiente figura:

Llamamos [b]ángulo inscrito[/b] a cualquier ángulo formado por dos cuerdas, las cuales tengan un punto en común.[br][br]Es importante notar que una de las cuerdas puede ser el diámetro. El diámetro es un tipo de cuerda.

Si dos ángulos inscritos en un círculo abren el mismo arco, entonces ellos son iguales y iguales a la mitad del ángulo central correspondiente. Es decir,

[math]\angle CDA=\angle CBA=\frac{1}{2}COA[/math]

[b]Demostración[/b]: Esta demostración se lleva a cabo en tres casos distintos.

[i]Primer caso[/i]: Uno de los lados del ángulo inscrito pasa por el centro de la circunferencia.

Como el triángulo ABO es isósceles, entonces [math]\angle OBA=\angle BAO=\angle CBA[/math].[br]Además, como la medida del ángulo exterior de un triángulo es la suma de los otros dos ángulos no adyacentes, entonces[br][math]\angle COA=\angle OBA+\angle BAO=2\angle CBA[/math]

[i]Segundo caso[/i]: El centro de la circunferencia es un punto interior del ángulo inscrito.

Sea BD el diámetro de la circunferencia que pasa por O y B. Sean [math]\alpha_1=\angle CBD[/math] y [math]\alpha_2=\angle CBD[/math]. Note que [math]\angle CBA=\alpha_1+\alpha_2[/math]. Por el primer caso se tiene que [math]\angle DOA=2\alpha_1[/math] y [math]\angle COD=2\alpha_2[/math]. Además, [math]\angle COA=\angle DOA+\angle COD[/math]. Por lo tanto, [math]\angle COA=2\alpha_1+2\alpha_2=2\left(\alpha_1+\alpha_2\right)=2\angle CBA[/math]

[i]Tercer Caso[/i]: El centro de la circunferencia es un punto exterior del ángulo inscrito.

Sea BD el diámetro que pasa por O y B. Sean [math]\alpha_1=\angle ABD[/math] y [math]\alpha_2=\angle CBD[/math]. Note que [math]\angle CBA=\alpha_2-\alpha_1[/math]. Además, por el Caso 1, se tiene que [math]\angle AOD=2\alpha_1[/math] y [math]\angle COD=2\alpha_2[/math]. [br]Entonces:[br][math]\angle COA=\angle COD-\angle AOD=2\alpha_2-2\alpha_1=2\left(\alpha_2-\alpha_1\right)=2\angle CBA[/math]

Un ángulo formado por la intersección de dos secantes es [math]\angle\alpha=\frac{1}{2}\left(AB-CD\right)[/math]

Medida del ángulo central basado en el arco es [math]\angle\alpha=\frac{1}{2}AB[/math]

La medida de un ángulo inscrito a dos cuerdas es [math]\angle\alpha=\frac{1}{2}\left(AB+CD\right)[/math] donde AB y CD son cuerdas.

Un ángulo es [b]semi-inscrito[/b] si tiene su vértice en la circunferencia, uno de los lados es una tangente y el otro una secante. [br][br]Veamos el siguiente ángulo semi-inscrito [math]\alpha[/math]

Todo ángulo semi-inscrito es igual a la mitad del ángulo central que abre el mismo arco.[br][br][b]Demostración[/b]: Consideremos el ángulo semi-inscrito ABC en la circunferencia con centro en O y sea E en la circunferencia tal que BE es diámetro.

Como AB es tangente a EB se tiene que [math]\angle ABC=90^\circ-\angle CBE[/math]. Además el ángulo inscrito [math]\angle CBE=\frac{\angle COE}{2}[/math].[br][br]Además [math]\angle COE=180^\circ-\angle BOC[/math]. Por lo tanto:[br][br][math]\angle ABC=90^\circ-\angle CBE=90^\circ-\frac{\angle COE}{2}=90^\circ-\left(\frac{180^\circ-\angle BOC}{2}\right)=\frac{\angle BOC}{2}[/math]