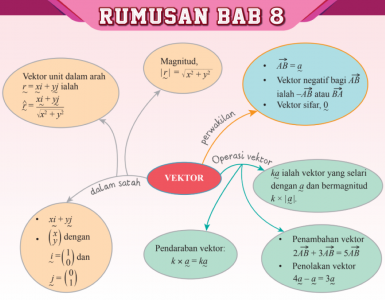
Vektor yang bermagnitud 1 unit dan selari dengan paksi-x dipanggil vektor [math] \undertilde{i}[/math] dan ditulis sebagai [math] \undertilde{i}=\binom{1}{0}[/math], [math] |\undertilde{i}|=1[/math].[br]Vektor yang bermagnitud 1 unit dan selari dengan paksi-y dipanggil vektor [math] \undertilde{j}[/math] dan ditulis sebagai [math] \undertilde{j}=\binom{0}{1}[/math], [math] |\undertilde{j}|=1[/math].

Koordinat titik B ialah [math]B(x,y)[/math].[br]Vektor kedudukan bagi titik B relatif kepada titik O ialah [math] \overrightarrow{OB} [/math][br]Vektor unit boleh ditulis seperti berikut:[br][center][math] \overrightarrow{OB}=x\undertilde{i}+y\undertilde{j}[/math] (gabungan vektor)[br][math]\overrightarrow{OB}=\binom{x}{y}[/math] (bentuk vektor lajur)[/center]Magnitud bagi vektor [math]\overrightarrow{OB}[/math] boleh dikira dengan menggunakan teorem Pythagoras[br][center][math]|\overrightarrow{OB}|=\sqrt{x^2+y^2}[/math][/center][br]Jika [math]\undertilde{r}=x\undertilde{i}+y\undertilde{j}[/math], maka vektor unit dalam arah [math]\undertilde{r}[/math] ialah[br][center] [math]\hat{\undertilde{r}}=\frac{\undertilde{r}}{|\undertilde{r}|}=\frac{x\undertilde{i}+y\undertilde{j}}{\sqrt{x^{2}+y^{2}}}[/math].[/center]

Contoh menentukan magnitud vektor [math]4\undertilde{i}+3\undertilde{j}[/math] dengan menggunakan kalkulator saintifik [br]1. Tekan [ menu ][br]2. Tekan [ 1 ][br]3. Tekan [ SHIFT ] [ + ][br]4. Skrin akan memaparkan: [br][center]Pol([/center]5. Tekan [ 4 ] [ SHIFT ] [ ) ] [ 3 ] [ = ] [br]6. Skrin akan memaparkan:[br][center]Pol(4,3)[br]r=5[/center]

Penambahan dua atau lebih vektor:[br][math]\undertilde{a}+\undertilde{b}=\binom{a_1}{a_2}+\binom{b_1}{ b_2}=\binom{a_1+b_1}{a_2+b_2}[/math][br][math]\undertilde{a}+\undertilde{b}=(a_1\undertilde{i}+a_2\undertilde{j})+(b_1\undertilde{i}+b_2\undertilde{j})=(a_1+b_1)\undertilde{i}+(a_2+b_2)\undertilde{j}[/math][br][br]Penolakan antara dua vektor:[br]Kaedah sama seperti operasi penambahan vektor boleh digunakan untuk operasi penolakan antara dua vektor. [br][math]\undertilde{a}-\undertilde{b}=\binom{a_1}{a_2}-\binom{b_1}{ b_2}=\binom{a_1-b_1}{a_2-b_2}[/math][br][math]\undertilde{a}-\undertilde{b}=(a_1\undertilde{i}+a_2\undertilde{j})-(b_1\undertilde{i}+b_2\undertilde{j})=(a_1-b_1)\undertilde{i}+(a_2-b_2)\undertilde{j}[/math][br][br]Pendaraban vektor dengan skalar:[br]Apabila suatu vektor didarab dengan suatu skalar, kedua-dua komponen [math]\undertilde{i}[/math] dan [math]\undertilde{j}[/math] juga didarabkan dengan skalar itu.[br][math]k\undertilde{a}=ka_1\undertilde{i}+ka_2\undertilde{j}[/math][br][br]Gabungan operasi aritmetik ke atas vektor:[br]Gabungan operasi aritmetik ke atas vektor perlu mematuhi peraturan operasi matematik. Operasi pendaraban dengan skalar perlu dilakukan terlebih dahulu diikuti operasi penambahan dan penolakan.[br][br][br]

Vektor kedudukan Rumah Samad ialah [math] -10\undertilde{i} + 10\undertilde{j} [/math] dan vektor kedudukan Kampung Samad ialah [math] -30\undertilde{i} + 35\undertilde{j} [/math] . Jarak di antara Rumah Samad dan Kampung Samad diukur dalam kilometer. Samad mahu berbuka puasa bersama-sama ibunya di kampung. Waktu berbuka puasa di kampung adalah pada jam 7.20 malam. Jika Samad bertolak dari rumahnya pada jam 7.00 malam dan memandu dengan halaju seragam 80 km/j sepanjang perjalanannya, adakah Samad sempat berbuka puasa bersama-sama dengan ibunya di kampung tepat pada waktunya? Tunjukkan pengiraan anda.[br][br][b][i][color=#0000ff][u]Jawapan: [/u][/color][br][/i][/b][br][b]Menulis hukum segitiga[/b][br][math] \overrightarrow{SK} [/math] = [math] \overrightarrow{SO} [/math] + [math] \overrightarrow{OK} [/math][br][math] \overrightarrow{SK} [/math] = ([math] -30\undertilde{i} + 35\undertilde{j} [/math]) - ([math] -10\undertilde{i} + 10\undertilde{j} [/math])[br][math] \overrightarrow{SK} [/math] = [math] -20\undertilde{i} + 25\undertilde{j} [/math][br][br][b]Menggunakan formula magnitud[/b][br][math] |\overrightarrow{SK}| [/math] = [math] \sqrt{(-20)^2 + (25)^2} [/math][br][math] |\overrightarrow{SK}| [/math] = 32.02 km[br][br][b]Mencari masa[/b][br]masa = 32.02 km [math]\div[/math] 80 km/j[br]masa = 0.4 jam @ 24 minit[br][br][math]\therefore[/math][b][u] [color=#ff0000]Tidak kerana dia akan sampai pada pukul 7.24pm[/color][/u][/b]

Arus air diberi oleh [math] \undertilde{v} [/math] = [math] 2\undertilde{i} + \frac{1}{2}\undertilde{j} [/math] ms[sup]-1[/sup]. Ahmad dan Ben masing-masing melayar kapal layar mereka dengan kelajuan [math] \undertilde{a} [/math] = [math] 5\undertilde{i} + 3\undertilde{j} [/math] ms[sup]-1[/sup] dan [math] \undertilde{b} [/math] = [math] 3\undertilde{i} + 2\undertilde{j} [/math] ms[sup]-1[/sup] . Kedua-dua kapal layar berlayar mengikut arah arus air.[br][br](a) Berapa kali gandakah halaju paduan kapal layar Ahmad berbanding halaju paduan kapal layar Ben?[br][br](b) Dalam perjalanan menuju ke garisan penamat, kapal layar seorang lagi peserta, Chong telah mengalami masalah dan tersasar dari laluan dengan halaju [math] \undertilde{c} [/math] = [math] 3\undertilde{i} - \frac{3}{2}\undertilde{j} [/math] ms[sup]-1[/sup] . Cari halaju panduan dan magnitud bagi kapal layar Chong.[br][br][b][i][color=#0000ff][u]Jawapan:[/u][/color][br][/i][/b][br](a)[br][br][b]Halaju paduan kapal Ahmad,[/b][br][br][i]A [/i] = [math] \undertilde{v} [/math] + [math] \undertilde{a} [/math][br][br][i]V[sub]A[/sub][/i] = [math] 2\undertilde{i} [/math] + [math] \frac{1}{2}\undertilde{j} [/math] + [math] 5\undertilde{i} [/math] + [math] 3\undertilde{j} [/math][br][br][i]V[sub]A[/sub][/i] = [math] 2\undertilde{i} [/math] + [math] \frac{7}{2}\undertilde{j} [/math][br][br][i]V[sub]A[/sub][/i] = [math] 7(\undertilde{i} + \frac{1}{2}\undertilde{j}) [/math] ......(1)[br][br][b]Halaju paduan kapal Ben,[/b][br][br][i]B [/i] = [math] \undertilde{v} [/math] + [math] \undertilde{b} [/math][br][br][i]V[sub]B[/sub][/i] = [math] 2\undertilde{i} [/math] + [math] \frac{1}{2}\undertilde{j} [/math] + [math] 3\undertilde{i} [/math] + [math] 2\undertilde{j} [/math][br][br][i]V[sub]B[/sub][/i] = [math] 5\undertilde{i} [/math] + [math] \frac{5}{2}\undertilde{j} [/math][br][br][i]V[sub]B[/sub][/i] = [math] 5(\undertilde{i} + \frac{1}{2}\undertilde{j}) [/math] .......(2)[br][br]Dari [i]V[sub]A[/sub][/i] dan [i]V[sub]B[/sub][/i][br][br][b]katakan[/b] [math] \frac{1}{7} [/math] [i]V[sub]A[/sub][/i] = [math] \undertilde{i} [/math] + [math] \frac{1}{2}\undertilde{j} [/math] [b]DAN[/b] [math] \frac{1}{5} [/math] [i]V[sub]B[/sub][/i] = [math] \undertilde{i} [/math] + [math] \frac{1}{2}\undertilde{j} [/math][br][br]Maka [math] \frac{1}{7} [/math] [i]V[sub]A[/sub][/i] = [math] \frac{1}{5} [/math] [i]V[sub]B[/sub][/i].[br][br][math] \frac{1}{7} [/math] [i]V[sub]A[/sub][/i] = [math] \frac{1}{5} [/math] [i]V[sub]B[/sub][/i][br][br][i]V[sub]A[/sub][/i] = [math] \frac{7}{5} [/math] [i]V[sub]B[/sub][/i][br][br][color=#ff0000][b][math]\therefore[/math] [u]Halaju paduan kapal layar Ahmad adalah [/u][/b][/color][b][math]\frac{7}{5}[/math][/b][color=#ff0000][b][u] ganda halaju paduan kapal layar Ben.[/u][/b][/color][br][br](b)[br][br][b]Halaju paduan kapal Chong,[/b][br][br][i]C [/i] = [math] \undertilde{v} [/math] + [math] \undertilde{c} [/math][br][br][i]V[sub]C[/sub][/i] = [math] 2\undertilde{i} [/math] + [math] \frac{1}{2}\undertilde{j} [/math] + [math] 3\undertilde{i} [/math] - [math] \frac{3}{2}\undertilde{j} [/math][br][br][i]V[sub]C[/sub][/i] = [math] 5\undertilde{i} [/math] - [math] \undertilde{j} [/math][br][br][b]Magnitud kapal Chong[br][/b][br]= |[math] 5\undertilde{i} [/math] - [math] \undertilde{j} [/math]|[br][br]= [math] \sqrt{5^2 + (-1)^2} [/math][br][br]= [b][math] \sqrt{26} [/math][/b][br][br][b][color=#ff0000][math] \therefore [/math] [u]Halaju paduan adalah [/u][math] 5\undertilde{i} [/math][u] - [/u][math] \undertilde{j} [/math][u] dan maginitud adalah [/u][math] \sqrt{26} [/math][u] bagi kapal layar Chong.[/u][/color][/b]

Vektor kedudukan bandar A ialah [math] -10\undertilde{i} + 10\undertilde{j} [/math] dan vektor kedudukan bandar B ialah [math] 10\undertilde{i} - 11\undertilde{j} [/math]. Bandar A, B dan C terletak pada satu garis lurus dengan keadaan jarak di antara bandar A dengan bandar C adalah dua kali jarak di antara bandar A dengan bandar B. Jarak di antara bandar diukur dalam kilometer. Cari[br](a) vektor [math] \overrightarrow{AB} [/math],[br](b) jarak di antara bandar A dengan bandar B,[br](c) vektor [math] \overrightarrow{OC} [/math].[br][br][b](a)[/b][br][br][math] \overrightarrow{AB} [/math] = [math] \overrightarrow{AO} [/math] + [math] \overrightarrow{OB} [/math][br][br][math] \overrightarrow{AB} [/math] = [math] -\overrightarrow{OA} [/math] + [math] \overrightarrow{OB} [/math][br][br][math] \overrightarrow{AB} [/math][br][br]= ([math] 10\undertilde{i} - 10\undertilde{j} [/math]) + ([math] 10\undertilde{i} -11\undertilde{j} [/math]) [br][br]= [math] 20\undertilde{i} - 21\undertilde{j} [/math] [br][br][b](b)[/b][br][br]Jarak di antara bandar A dengan bandar B[br][br]= |[math] \overrightarrow{AB} [/math]|[br][br]= [math] \sqrt{(20^2 + (-21)^2} [/math][br][br]= 29 km[br][br][b](c)[/b][br][br][math] \overrightarrow{OC} [/math] = [math] \overrightarrow{OA} [/math] + [math] \overrightarrow{AC} [/math][br][br][math] \overrightarrow{OC} [/math] = [math] \overrightarrow{OA} [/math] + [math] 2\overrightarrow{AB} [/math][br][br][math] \overrightarrow{OC} [/math] [br][br]= ([math] -10\undertilde{i} + 10\undertilde{j} [/math]) + [math] 2(10\undertilde{i} - 10\undertilde{j}) [/math][br][br]= [math] 30\undertilde{i} - 32\undertilde{j} [/math]

https://www.geogebra.org/3d/w33qzxfs

https://www.geogebra.org/3d/rjtbg6pv