Dimensi Tiga
[b]Dimensi tiga[/b] merupakan bangun ruang yang terbentuk dari 3 elemen yaitu titik, garis, dan bidang. Titik adalah lukisan tanda noktah yang dibubuhi nama menggunakan huruf kapital. Suatu titik tidak memiliki besaran dan tidak berdimensi. Garis adalah himpunan titik-titik yang hanya memiliki ukuran panjang dan [b]berdimensi satu[/b]. Sedangkan bidang adalah himpunan titik-titik yang memiliki ukuran panjang dan luas, sehingga dikatakan [b]berdimensi dua[/b]. [br][b][color=#ff0000]Adapun materi yang akan kita pelajari dalam dimensi tiga ini adalah[/color][/b][br][*] [b][color=#0000ff]Jarak titik ke titik[br][/color][/b][/*][*][b][color=#0000ff] Jarak titik ke garis[br][/color][/b][/*][*][b][color=#0000ff] Jarak titik ke bidang [/color][/b][/*]
[color=#9900ff][b]Jarak Titik ke Titik[/b][/color][br]Ilustrasi di bawah ini memeragakan jarak antara titik A dan titik B. [br]Jarak antara titik A dan titik B sama dengan panjang ruas garis AB.[br]
Lalu bagaimana cara menentukan jarak antar titik dalam ruang? masih ingatkah kalian dengan teorema pythagoras?[br]Ya, teorema pythagoras digunakan untuk menentukan panjang sisi salah satu segitiga siku-siku.[br][img]https://1.bp.blogspot.com/-zDOZxESPMMw/X4hM63dytYI/AAAAAAAADhg/4WVeuGWAT3ET1fwPz13j-BCq2YGdMLzqQCLcBGAsYHQ/w640-h250/pitagoras_segitiga_sikusiku.jpg[/img]
[u][b][color=#ff0000]Contoh[/color][/b][/u][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik I merupakan titik tengah rusuk DH. Tentukan jarak antara titik I dengan titik F.[br]Langkah Penyelesaian[br]1. Gambarlah kubus ABCD.EFGH[br]2. Hubungkan titik I dan titik F dengan sebuah garis.[br]3. Buatlah segitiga siku-siku yang melalui titik I, F, dan satu titik lain (misal segitiga IFH)[br]4. Hitunglah panjang ruas garis IF menggunakan teorema Pythagoras.
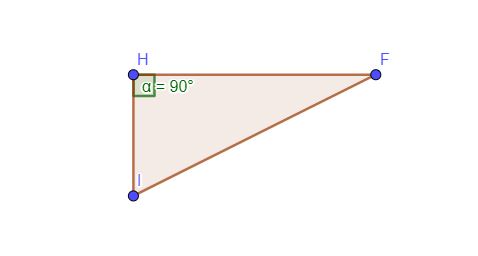
[size=100]Untuk menentukan jarak antara titik I dan titik F, buatlah segitiga IFH siku-siku di H.[br]Oleh karena I titik tengah DH, maka[br][math]IH=\frac{1}{2}\times DH=\frac{1}{2}\times6=3[/math][br][math]HF=6\sqrt{2}[/math] , HF diagonal sisi[br][math]IF=\sqrt{IH^2+HF^2}[/math][br][math]IF=\sqrt{3^2+\left(6\sqrt{2}\right)^2}[/math][br][math]IF=\sqrt{9+72}[/math][br][math]IF=\sqrt{81}[/math][br][math]IF=9[/math][br]jadi, jarak antara titik I dan titik F adalah 9 cm.[/size]
[color=#9900ff][b]Jarak Titik ke Garis[br][/b][/color]Jarak titik ke garis adalah [b]ruas garis yang tegak lurus[/b] atau terpendek dari sebuah titik terhadap sebuah garis. Misal A adalah titik dan g adalah garis. Jarak titik A ke garis g adalah panjang ruas garis AB dengan B terletak di garis g, dan AB tegak lurus dengan garis g.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAZEAAAGiCAYAAAAmz/tUAAAgAElEQVR4Ae2dXagmxZnHD65uwgZxZjSiWTfxI7sX+VjmIpsPIuygYzQJCeO3Jm4c4mISL5ZBkARvZDEsm9yYNbAO5GKSXCRLLlZIUGGDSIgSSCRjJBhiNGMwYQcVhrgRRQK1/M/4nFOn3u5+q6urP6r7V/DSX9XVVb+n5/znqaqnesORIAABCEAAAokENhLv4zYIQAACEICAQ0R4CSAAAQhAIJkAIpKMjhshAAEIQAAR4R2AAAQgAIFkAohIMjpuhAAEIAABRIR3AAIQgAAEkgkgIsnouBECEIAABBAR3gEIQAACEEgmgIgko+NGCEAAAhBARHgHIAABCEAgmQAikoyOGyEAAQhAABHhHYAABCAAgWQCiEgyOm6EAAQgAAFEhHcAAhCAAASSCSAiyei4EQIQgAAEEBHeAQhAAAIQSCaAiCSj40YIQAACEEBEeAcgAAEIQCCZACKSjI4bIQABCEAAEeEdgAAEIACBZAKISDI6boQABCAAAUSEdwACEIAABJIJICLJ6LgRAhCAAAQQEd4BCEAAAhBIJoCIJKPjRghAAAIQQER4ByAAAQhAIJkAIpKMjhshAAEIQAAR4R2AAAQgAIFkAohIMjpuhAAEIAABRIR3AAIQgAAEkgkgIsnouBECEIAABBAR3gEIQAACEEgmgIgko+NGCEAAAhBARHgHIAABCEAgmQAikoyOGyEAAQhAABHhHYAABCAAgWQCiEgyOm6EAAQgAAFEhHcAAhCAAASSCSAiyei4EQIQgAAEEBHeAQhAAAIQSCaAiCSj40YIQAACEEBEeAcgAAEIQCCZACKSjI4bIQABCEAAEeEdgAAEIACBZAKISDI6boQABCAAAUSEdwACEIAABJIJICLJ6LgRAhCAAAQQEd4BCEAAAhBIJoCIJKPjRghAAAIQQER4ByAAAQhAIJkAIpKMjhshAAEIQAAR4R2AAAQgAIFkAohIMjpuhAAEIAABRIR3AAIQgAAEkgkgIsnouBECEIAABBAR3gEIQAACEEgmgIgko+NGCEAAAhBARHgHIAABCEAgmQAikoyOGyEAAQhAABHhHYAABCAAgWQCiEgyOm6EAAQgAAFEhHcAAhCAAASSCSAiyei4EQIQgAAEEBHeAQhAAAIQSCaAiCSj40YIQAACEEBEeAcgAAEIQCCZACKSjI4bIQABCEAAEeEdgMDCCLzrzp+602750crvsd/8cWEkaG4OAohIDoqUAYFCCHz/6Esr4mGC8plv/KqQVlDNKRFARKZkDeoCgZ4JSChMNMLt22//Sc9Pp/g5EkBE5mhV2gSBGgK7b3u0VkQkKvf+8Pc1d3IaAtUEEJFqLpyFwOwIfPkHv9shIBobkffheyRXfv2Xs2s3DeqXACLSL19Kh8BkCOz/6i92CMYXv/esq+re+u0Lr06mzlRk+gQQkenbiBpCoDMBzbzyPQ7tSyyqBtrlsZAgEEsAEYklRT4IFExAXocvIvJKLIVTfnVMgkAsAUQklhT5IFAwgXDsw/c2QoGR2BAzUrCxB646IjIwcB4HgaEJfOvR4zu8EM3Q8sc9qrq6iBkZ2krlPg8RKdd21BwCUQQ048rvyqqagRV2aREzEoWWTM45RITXAAIzJiCPI4wNqYoFqerSqso3Y1Q0LZEAIpIIjtsgUAKBMDZEglKVqrq0qjyWqns5t2wCiMiy7U/rZ07gg3f/fEdXlt+tFbPvj53MHBXNSySAiCSC4zYITJ1AlXcRIxx+Hn8W19TbS/3GIYCIjMOdp0KgdwJV0ei+QMTsy5MhQaCJACLSRIdrECiYQBgbEiMaVXmIGSn4JRig6ojIAJB5BASGJqCZVaEgxIhB1X23ffvpoavP8woigIgUZCyqCoFYAmFsSJulTMIpwcSMxFJfZj5EZJl2p9UzJqAZVaEXojiQ2BQKkMpS1DsJAlUEEJEqKpyDQMEEqgIHY7qyrMlVK/sSM2J02IYEEJGQCMcQKJxAuISJv2JvbNPCQflwva3Ycsg3fwKIyPxtTAshAAEI9EYAEekNLQVDAAIQmD8BRGT+NqaFEIAABHojgIj0hpaCIQABCMyfACIyfxvTQghAAAK9EUBEekNLwRCAAATmTwARmb+NaSEEIACB3gggIr2hpWAIzJfAfffd5y7Zf5nbc+ZZmz/t6xxpeQQQkeXZnBZDIJnA66+/7q6+5jp39jnnufd84DL34Y/etPnTvs7pmvKQlkMAEVmOrWkpBDoT+NSnb3K7zzrH7b/mtsrfGWee7ZSHtBwCiMhybE1LIdCJwEMPPeR2n/lWd+nVn68UEAmLrp1+xm734IMPdnoWN5dDABEpx1bUFAKjEjhw5VXuvAvfXSsg5p0ozzXXXjdqXXn4cAQQkeFY8yQIFE3gwove6d5/6bVrRUR53nHBhUW3lcrHE0BE4lmREwKLJrCxseEuvepkV9aBm25xT/z329y3vvYP7tO3/NMOYbnkylud8pKWQQBLL8POtBICnQm882//zn3o8hs3BeM///1i5x7f2PxJTKwrS1t5IvJaSMsggIgsw860EgKdCdxw46fceRe+Z1MwJBwmIl/910t2iIjGRD7+iU92fh4FlEEAESnDTtQSAqMT0Iwrzc669bZrtwTk/x57k1PXlnkimp11xq49TjO5SMsggIgsw860EgJZCNx880H3b//yV1si8th3LtgSEAnJGXvOdtddf2OWZ1FIGQQQkTLsRC0hMAkCr7/6gnvh4bdsiciXbv/HHRHrnzxwFRHrk7DUcJVARIZjzZMgUD6BE/dvCcj//s+b3Z49J9fO+sjlV7h7vvYf5bePFrQmgIi0RsYNEFgwgWcObImI+8NdCwZB040AImIk2EIAAs0E/nzCuaO7tkXklaPN+bm6CAKIyCLMTCMhkIHA8Xu2BeTX+zIUSBFzIICIzMGKtAECQxCQcLwRYOgkKCQIOOcQEV4DCEBgPQF1XZmAqEtLXVskCCAivAMQgEAUAQ2im4hocJ0EgTcI4InwKkAAAs0E5HU8ef62iGiaLwkCbxBARHgVIACBZgJebMimmDTn5urCCCAiCzM4zYVAawLEhrRGtqQbEJElWZu2QqAtAWJD2hJbXH5EZHEmp8EQaEHAjw15am+LG8m6FAKIyFIsTTshkELAjw1hmZMUgrO/BxGZvYlpIAQSCRAbkghuWbchIsuyN62FQDwBYkPiWS04JyKyYOPTdAg0EiA2pBEPF08SQER4EyAAgVUCYWwIy5ysMuLMJgFEhBcBAhBYJUBsyCoTzlQSQEQqsXASAgsmQGzIgo3fvumISHtm3AGBwQk8++yz7s4773TXX3+9e+KJJ/p9PrEh/fKdWemIyMwMSnPmR0CisXv3brexsbH580XkpZdeyi8qxIbM7yXqsUWISI9wKRoCXQlIJC666KJN8fjKV77iHnjgga0idWzCojz+ta1MbXfC2JDXjrUtgfwLI4CILMzgNLcsAocPH94UCm399N3vfndLQExI5K2o26tTIjakE74l3oyILNHqtLkYApdffvlmV5Zf4R//+MdbAmLi8oUvfGHznMZNOiViQzrhW+LNiMgSrU6biyEgL0NCYkndWzY+IuHwU5jXvxa178eG8AncKGRk4hvrvAMQmDQBCYZ+Eg/93ve+9216HNr6SdckIqGw+HnW7hMbshYRGVYJ4ImsMuEMBCZDwAbPTUwkFNoPxz5sjETbpERsSBI2bsIT4R2AwOgEJAga56hK8jAUGyLx0E+zsPwpvrpH95vIKH9SIjYkCRs3ISK8AxAYnYAGwyUQYReVX7EqoVHXlX4SEN1vg+z+fdH7xIZEoyLjTgJ0Z+3kwREEBiegP/4SAptZJW9C4hB6HH7FJCrmnWhr9/p5oveJDYlGRcZVAojIKhPOQGAUAtYVJVExgZB3onEOu2YV07HOK8BQgtIpERvSCd/Sb0ZElv4G0P7JEZAoyLOwbioJinkqnQWjqrXEhlRR4VwkAUQkEhTZIDAEAXVhaUaWknkbNq3XvBPFjSTPwgobQWxISITjlgQQkZbAyA6BPgmYYJiQ2LMkLv4gunknYT7LH731Y0OePxR9GxkhYAQQESPBFgIjE5BQmDiEYyBWNZ3XmIktyuhHs1ue6G0YG/LyI9G3khECRgARMRJsITAyAZtxFSsMii2piy+JagqxIVGYyNRMABFp5sNVCAxGQOMc1mVV54lkrQyxIVlxLrUwRGSplqfdkyJgXVk2eK6xkV5mYlmriQ0xEmw7EkBEOgLkdgjkICDB0CC5jXWYmKwLOkx+NrEhyei4cScBRGQnD44gMDoBdWtpXMSERNu6oMPkyhIbkoyOG3cSQER28uAIApMhIO+kKuhQ3kmnMRNiQyZj4zlUBBGZgxVpw+wJyDuxGBJFr3cSEWJDZv++DNlARGRI2jwLAgEBiYE8C+uy0rhI04C6BuA7RasTGxJYgMOuBBCRrgS5HwIdCJh34Y9/aF/fENHiitnTi0ece3zj5O+pvdmLp8DlEUBElmdzWjwRAvIozANR0KBEIxQVzdZa5520ag6xIa1wkXk9AURkPSNyQKAXAhKIcHzDurYkHLoWeiidvBNiQ3qx49ILRUSW/gbQ/lEIWHBh+DEpeSL6KWm8xPdMJDqdErEhnfBxczUBRKSaC2ch0CsB68ry176SaMjzkDdiSYPsOtdpMN0KIzbESLDNSAARyQiToiAQS0DdVaE4qKtK58JvpcsbUf5OidiQTvi4uZ4AIlLPhisQ6I2AdWdp3EP7SurakojYsT3cBtftOGlLbEgSNm5aTwARWc+IHBDohYCm8Uo0rEvLljrxAwmtOyv0TlpViNiQVrjI3I4AItKOF7khkI2AxMIf67CZWSYY/sB6UwDi2goRG7IWERnSCSAi6ey4EwJZCcgjkWein03/1b4/0J70QGJDkrBxUxwBRCSOE7kgkIWABsnVbeV7IH7B8kJMSLRVXr97y88bte/HhihS/bVjUbeRCQKxBBCRWFLkg0BHAhIDeRgmEhpUr4pGV9eVvJJwgD3p8cSGJGHjpngCiEg8K3JCoBMBiYMNppuQ2La3tbKIDelkM25eTwARWc+IHBDoTEBehTwP8z7kaeinab2+d2LTeTt1YVltiQ0xEmx7JICI9AiXoiFgBGz6bl0XlQUfmmeirQbUO4nJcwe3V+x9/pBVhS0EshJARLLipDAIrBKQEEgU1GXVlGwpFHkrJibarxOeprIcsSGNeLiYjwAiko8lJUGgkoBN3Q0XW6zKrO4seSD++ImEpLVH4ndl8d2QKtScy0QAEckEkmIgUEdAgiDPQgKxLqnbSz9LNhBfNyXY8q1s/WVONEOLBIGeCCAiPYGlWAj4BGxMpClwUN6GvA5fRMyLabUAo2JB7OuFxIb4ZmC/BwKISA9QKRICIQGbnSWPRCIhcQiTBEbXfa/DRMSWQgnvqTwmNqQSCyf7IYCI9MOVUiGwQsAXEuveUneVxMOm+doHqexmE5ZWg+vEhhg+tgMQQEQGgMwjIGAE1GUlYfBnYElQ9JOg+APoEg6d97u3rJzarT+gfnSX25ylVZuZCxDoTgAR6c6QEiCQREBdVfbT4LsldWdpJpcJTVXXl+Vd2RIbsoKEE/0SQET65UvpEGhFQGJi4iEvxB8fWVsQsSFrEZEhPwFEJD9TSoRAMgF1Z0k4NJDueydRBfpdWcSGRCEjU3cCiEh3hpQAgWkQIDZkGnZYWC0QkYUZnObOlACxITM17PSbhYhM30bUEALrCRAbsp4ROXohgIj0gpVCl0xAYxk268qfstsrE2JDesVL4fUEEJF6NlyBQGsCGhS3uA/bKi6k1TTdtk99+ZHtZU6IDWlLj/wdCSAiHQFyOwSMgAUHSjwUea6fCYmdk8hk906IDTETsB2BACIyAnQeOU8CtkSJH9uhri0/cFBiojgQ5W21lEkdMmJD6shwfiACiMhAoHnM/AlIHJqWe5e4hN5J61iQECOxISERjgcmgIgMDJzHzZeAvAx5GOuSPBDli8m7rixHbMhaRGTolwAi0i9fSl8QAS2g2GqxxK5siA3pSpD7MxBARDJApIhlE9BAubqxrKvKHxPplQyxIb3ipfA4AohIHCdyQaCWgLqn/EUTrVur83hH7RPfuKD1sewLhhobIUFgBAKIyAjQeeQ8CVQNnKt7qxfPhNiQeb5EBbYKESnQaFR52gRs4Nz3TrSv76Rn8078rizFiZAgMBIBRGQk8Dx2/gRsWXf79K26ufTrLCTEhsz/5SmohYhIQcaiqtMjIEGQh/HAAw80RqJr2RNN6dXge+dEbEhnhBSQjwAiko8lJS2MgMY6zLvQVl1WEooskehNLIkNaaLDtYEJICIDA+dx8yAgD8QERIPnNr3XzulYIpN9nSxiQ+bxAs2oFYjIjIxJU4YjII9DguHPvNIaWeaRmJiYd6Iuryweij+gLo+EBIGRCSAiIxuAx5dHQN6FRCKMTtexREPXJRomJLbtPKAuVMSGlPfCzLzGiMjMDUzz8hPQILmEwfdC9BQJiC8shw8f3swnryXMm1SrV45uBxfy3ZAkhNyUnwAikp8pJc6cgHkZ/oem1FUlYdE1P0lYwnP+9Vb7flcWsSGt0JG5PwKISH9sKXmmBORVSDC04KIl8zo01ddP8kyyiIhiQ/xP4CpinQSBCRBARCZgBKpQFgGNecjD8Lu0JCg6DmdjVXknSa0lNiQJGzf1TwAR6Z8xTyiUQCgIfjPkcSgS3fLI45Bg+DOw6rwTv5zofWJDolGRcVgCiMiwvHlaIQQsDkTiEDMoboJh8SE2btL0pcNoFIoN0UC6rdirYxIEJkIAEZmIIajGtAjI07AuK3kY2lccSN00XXkk4RpZui8cI0lqpT+gTmxIEkJu6o8AItIfW0ounICEQV5IGI2u8Y8qcVB+TeeV96I8/uytTij82JAXj3QqipshkJsAIpKbKOXNkoAEwQbP5WHoJ89D3VZ13kkWEMSGZMFIIf0RQET6Y0vJMyJgYxwSD3kmfleXzskDyeZ5+NzoyvJpsD9BAojIBI1ClaZFwAbN5YnYbCzVUB6IxMUXFHknyu/nS24NsSHJ6LhxOAKIyHCseVKhBCQSTbOsJBjhuEkWr4TYkELfmGVVGxFZlr1pbUsCtpyJZmY1JQmJhEaD6uvyNpWz4xqxITtwcDBNAojINO1CrSZCQB6FxjzUlbUu2VLw6/JFXQ8/gUtsSBQ2Mg1PABEZnjlPLIyAjXn40ehVTcgqIsfv2Q4uJDakCjfnJkIAEZmIIajGdAnYzCyJSVV8iGpu3VlNYyetWvjrfdsiQmxIK3RkHpYAIjIsb55WKAH7kqFN8VUQojwTiYeExQbWNTOrcyI2pDNCChiOACIyHGueVDiBcDqvBMX/SWiyJGJDsmCkkGEIICLDcOYpMyEgz0PehmZhqetKPw2613VztW52GBuiab4kCEyYACIyYeNQtQUS8GND9BEqEgQmTgARmbiBqN7CCBAbsjCDl99cRKR8G9KCuRAgNmQullxUOxCRRZmbxk6agB8boim+JAgUQAARKcBIVHE4AjFfMeytNsSG9IaWgvsjgIj0x5aSCySggMJ1kem9NIvYkF6wUmj/BBCR/hnzhEII2DpZ2eI92rSb2JA2tMg7IQKIyISMQVXGJyBPRD/FgwyWiA0ZDDUPyk8AEcnPlBILJmDrZNWNjehDVAosVD79siRiQ7JgpJBxCCAi43DnqSMSUMS5RKLK25BI2PpYvmAoQl0eir/MSbYodWJDRnwbeHRXAohIV4LcXxwBLVUiMZAoaPwjHEj3F1v0RcPuyfrhqTA2RAPsJAgURAARKchYVDUPAXkhtuquiYSEwbqwbIBdIqN1sdRtJa9Dnkn2RGxIdqQUOCwBRGRY3jxtQgTkgcjr8LuptK+PS2mrX1WXV9Ym+LEhEhQSBAojgIgUZjCqm5+AhEJeiHVzmXeibbbB86pqExtSRYVzhRFARAozGNVNJyCvQz91V9UlXQvHRCQuEpPs3VnEhtSZgfMFEUBECjIWVe1GwLqtzLuQB1LXXaXzmsUVeid2b7eaOOeIDemMkAKmQQARmYYdqMUABORJaLzDPAoJgoRFnkc4Q8uvjgbVNcCu7i0bfPevJ+0TG5KEjZumRwARmZ5NqNFABMJuK83YahIJiU+d59K6ysSGtEbGDdMkgIhM0y7UaiACEgaJiXV1ydvQvu+xZK8KsSHZkVLgeAQQkfHY8+SBCFR5D+qi8s9rX15IU/xItur6sSFP7c1WLAVBYAwCiMgY1HnmoAQ040oD5BIJiYXGP5qm71r8iPLYT95KtuTHhmiGFgkCBRNARAo2HlWPI6AuKxMDdVXZjCsbYK8rRYJjM7SyrZNFbEgdbs4XSgARKdRwVLsdAXkhWtrExETbdQPp7Z4QmZvYkEhQZCuFACJSiqWoZxYC8iwkIDED6fI+lN8fO+lciSfPd+7xjZM/TfMlQaBwAohI4Qak+vUEqrqrNLah7qx1A+m6bt1eTTEk9U+vuBLGhmiWFgkChRNARAo3INWvJmCD5woSrBIT/y4bSPe9E+v2UhdYtkRsSDaUFDQdAojIdGxBTTIS0BiIhEDehKVwWq+dt60NpNs0X4lKNi+E2BDDzHZmBBCRmRmU5mwTkAdiiy1q37wLdWnZ+e3cPe8RG9IzYIofiwAiMhZ5njsoAYmIrX9lYiIvxWJHeq8MsSG9I+YB4xBARMbhzlNHIiAxsY9OmZio20reSbauq7BtYWzIa8fCHBxDoFgCiEixpqPidQQ09uF3V2lf4xyhSAwWO0JsSJ2pOD8DAojIDIxIE3YS0BLv8jIsmNC6seriPeSdyBPxZ2fpXLZEbEg2lBQ0PQKIyPRsQo06EpDH4QuCBEXjH6EnEj7GYkfU3ZUt+bEhR3ed/BhVtsIpCALjE0BExrcBNeiJgLqrbLqujX8o7kPnq1Kdp1KVN/ocsSHRqMhYJgFEpEy7UetIAvJAJCRhd5U8lfCbIcqrX7ZEbEg2lBQ0XQKIyHRtQ80yEJDXYYPs1l1V5Z3YuEnWCHViQzJYkCKmTgARmbqFqF8vBDQ+Iu/Eurlsa4KT5aHEhmTBSCHTJoCITNs+1K5nAuadaEZXtm+GqM7EhvRsOYqfCgFEZCqWoB7zIkBsyLzsSWtqCSAitWi4AIEOBIgN6QCPW0sigIiUZC3qWgYBYkPKsBO1zEIAEcmCkUKmRKCXeI82DfRjQ54/1OZO8kKgOAKISHEmo8JNBLRcSV0wYdN92a6FsSEvP5KtaAqCwBQJICJTtAp1SiagAELFgYyWiA0ZDT0PHocAIjIOd57aEwELGly3TlZPj3eO2JDe0FLwNAkgItO0C7VKJKCuLAUOKpBw8ERsyODIeeD4BBCR8W1ADTIT0PpXWhsrHGDXsSLSFVgoj0X5si75TmxIZktSXAkEEJESrEQddxDQH34JwOHDh1eEQhnteyLa+oJhS5vYVkKSNREbkhUnhZVBABEpw07U0iMg8TAhsK4rf80reRz+dX9fCyxq8F1lZPVCiA3xLMTukgggIkuy9ozaqrEPCYIvEJqVpfMSEVtcUVutidX7QDuxITN6u2hKGwKISBta5J0cAXkT8iz8Lxlq35Z7H2SAndiQyb0XVGg4AojIcKx5Us8E5IWYeJiHIkHR+V7Ti0ece3zj5O+pvb0+isIhMDUCiMjULEJ9OhOwb4WE3kn4JcPOD7ICiA0xEmwXSAARWaDRl9JkjY3IC9FMLvNMtM06oE5syFJeJ9pZQwARqQHD6TIISBA0jVeD5xKNuqTZWxofyb4kCrEhdcg5vxACiMhCDD3HZsrL8D0MdV9JKHqfieXDJDbEp8H+AgkgIgs0+hyaLA/EBERTfcMBdR1LZJq8k84ciA3pjJACyieAiJRvw0W2QB6HRMSfeaWBc50LB9SVV11e2T0UYkMW+e7R6J0EEJGdPDgqgIC8C4mFPBA/6VgCousSDfNUbJt1QJ3YEB89+wsmgIgs2PilNl2D5BIG3wtRWyQgvrDY8ijyRMK8ndtObEhnhBQwDwKIyDzsuKhWmJfhr5elrioJi675ScISnvOvJ+8TG5KMjhvnRQARmZc9F9EaeRUSDH8VXvM6NNXXT/JMsouIHxuiSPXXjvmPZB8CiyKAiCzK3PNorMY85GH4XVr2RcNwNlaVd9KZArEhnRFSwHwIICLzseUiWmIiIY9Dkeh2LI9DguHPwKrzTjqDIjakM0IKmA8BRGQ+tpx9S9QtJQ/EFwprtAmGxYcor0RFQpM1ERuSFSeFlU8AESnfhotogTwOiYJ+VTOtdD1cI0t5wzGSzrCeO7i9Yu/zhzoXRwEQKJ0AIlK6BRdSf5vW27T2lYRE03nVtaUxEn/2VhZMxIZkwUgh8yKAiMzLnrNujTyNJhHpvfF+VxbfDekdNw8ogwAiUoadFl1L66qywfOq7qxBAPnLnGiGFgkCEHCICC/B5AmoW8qm9Nq4iLqtsi5jso6CYkHs64XEhqyjxfUFEUBEFmTskpsqb0QeSDh4rrGP7IPnVaCIDamiwjkI4InwDpRHQJ6JPBHzSrSVuGhab2/eCbEh5b0o1HgQAngig2DmIX0QkHei+JDQO8kuJP6A+tFdzmmWFgkCENgkgIjwIkyagLwOdVmtW4lXXVrK18vsLWJDJv2OULlxCSAi4/Ln6Q0EbKFFv9tKA+z6+FR2b6OuHsSG1JHhPAQ2CSAivAiTJKCuKpuRJdHQeEfYbaUpv71P9/W7sogNmeS7QqXGJYCIjMufp9cQsLWvNOZhSV1W8kosXsQ8FImNzvl57Z7OW2JDOiOkgHkTQETmbd9iWyevQz8/mbCoK0s/jX+YkGibfZkTYkN8/OxDoJIAIlKJhZNjElBXlkRB3Vh+krchr8OSdXn1sk6WHkJsiKFmC4FaAohILRoujEVAHkWViOichMRPtuCify7bPrEh2VBS0HwJICI926T7bJsAAA9gSURBVPaee467Q4eed4888nLPT5pP8eaJyOuwb4eYsKhLy0/yVkJh8a8n77/8yPYyJ8SGJGPkxvkTQER6tvG+fb92GxuPb/7OP//JTUE5duy1np9afvESB3ke8jSUbDwkHPfQuEgvIkJsSPkvES0YhAAi0iPmo0df2RIQExLbSlzuuusPbsmCIo+jLumaBMTiQezLhf44icWRZJ+VRWxInVk4D4EVAojICpJ8JyQSJhpN2wMHnnHq9lpa0uwreRIxsR4SE3km+lkEu/bV5dUkRklMiQ1JwsZNyySAiPRs9/vvP+EOHnwuSkwkNBKUI0de7LlW4xevsQ4TBRMDeRnmeVTV0LwR/74YAaoqq/EcsSGNeLgIAZ8AIuLT6Hlf3oY/RtLknZigSITmmiQYEg55E74waIyjThw0JqLxEf2aBCeZGbEhyei4cZkEEJER7H7ixJ83u6/aCMqcZ3ipO0qiEQYPqrurN7GoszuxIXVkOA+BSgKISCWW4U5qYF0eimZurfNMdH3XrqObM7w0aD/HpG4uDaiH3ok/yN5ru7U+ln3BUGMjJAhAoJEAItKIZ9iLiiXRYHysoOzd+9RsZ3jJO9EYiLwRv6urrpsri6WIDcmCkUKWRQARmai92w7Iq2tMHo26yuaWNA6icRITk17GQgTN78pSnAgJAhBYSwARWYto/AxtBWWuM7w0tVdConGS7InYkOxIKXAZBBCRwuys6b9tBuTnJCgSD4mIRbFnNR2xIVlxUthyCCAiBdu67ZTh0md42VIovXgixIYU/C+Bqo9JABEZk36mZ891hpctvihM2rcZW9nHRIgNyfQmUswSCSAiM7P6nGZ4WdyIiYe6svy1s7KZzh9Ql0dCggAEogkgItGoysuoAXl1YcXEnyjP1GZ4hdN7exEQmZXYkPJebmo8GQKIyGRM0W9FSp3hpa4rTfHNvsii4X7l6HZwId8NMSpsIRBNABGJRjWfjBIUzdqK9VDmNMNrxYp+VxaxISt4OAGBdQQQkXWEZn59aTO8dphTsSH+J3AVsU6CAARaEUBEWuGab2ZbFFJLqcR4KLNYw6siNuSKK65wn/vc59z999/vXn311fkanJZBIBMBRCQTyDkVo8Ud267hpQH84r7SGMSG/OlPf9paWkUzwU455RT3sY99zN17773u6aefnpOJaQsEshFARLKhnGdBmjIsgZDnEeOhaIaXBGjya3gpNkQD6bZir46dcz/72c/c3Xff7S6++OIdgiJRee973+vuuOMO9/DDD8/T2LQKAgkEEJEEaEu9pdQZXpX28gfUa2JDjh8/7r75zW+6G264we3atWuHqOhY53Vd+UgQWCoBRGSplu/Y7uIFxY8NefFIFA15IPJE5JHIM/F/8lzkwciTIUFgSQQQkSVZu6e2FjfDK0NsiMZINFaiMRONnfiCorEVEgSWQgARWYqlB2hn2xleGmMZZVHIiK6sNrg0i0uzuTSrS7O7Tpw44fbt2+fuuusud+zYybGWNuWRFwIlEUBESrJWQXVtO8NLX3McZIbXALEhEhTzTPbu3VuQ1agqBNoTQETaM+OOlgRSZ3j1MmW4IjakZXPWZj9w4MCWiMgbIUFgzgQQkTlbd4JtG31APogNyY1IXVn+TC66s3ITprypEUBEpmaRBdVncEEJP4H7RmxITuR0ZeWkSVklEEBESrDSAurYdobXwYPPOXWTtUrH79kOLqyJDWlVXkVmurIqoHBq1gQQkVmbt7zG5Z7h9eCDD7oDV17lLrzonZvjFBf8zZvcNftPcw/91+3Z4dCVlR0pBRZAABEpwEhLraJmeMlD0cytmCVX/Bler7/+urv55oNu95lvdedd+G73/kuvdZdceevmVse795zlPvXpm5zy5Up0ZeUiSTklEUBESrLWgutqn/2NXcPrnHM/4U7ffba79OrPu/3X3Lby0/kz9pztrr7mumxU6crKhpKCCiKAiBRkLKp6ksD6Afkvubecft6KcFSJyZln/7W77777OqOlK6szQgoolAAiUqjhqPZJAlWCcuppF7v3fOCyKBH5+w9d4S7Zf1lnnHRldUZIAYUSQEQKNRzVXiVw5MiLTkvR/8Wpu92HP3pTlIjsO/DPbs+ZZ60W1vIMXVktgZF9NgQQkdmYkoYYAYlCrIgo36mn7u60hhddWUae7RIJICJLtPrM2/yRy6+I7s5St9eb3vzBrdlfKZ/9pSur+oX61qPH3ZVf/6V7++0/cafd8qPN3wfv/rn78g9+t3WDju2abbcuslMEAUSkCDNRyTYENFB+9jlxA+unn3GuO+Uv7tgSEX8qsb43r680rlvDi66sVet85hu/WhEHEwlt33XnT91vX3jVISKr7Eo7g4iUZjHqG0Xg+htu3JzC2zTFV1OA//LN+ysFxBcT7WusRTEr4Wd/6cpaNYe8D18w6vYlJPqF11dL5MyUCSAiU7YOdUsmoCDC666/sTbY8IxdezavK1/VDK9QRPzjAweecRrEV6Ira6eJ1FUVikLb450lcjR1AojI1C20oPq1/WOj/8Xqf73qe69LDz30kPv4Jz65tezJOy64cHMZFC2HUpUkKBIJXzSa9s899zKWffdA+uMfZk+du/eHv9/Kpf2qfJZ/KyM7RRBARIow0zIqaX9EUrYSk9wpblHI77iNjVvdxsbb3Gc/+5P2i0LmrvSI5UnMQ9vtvu1R99hv/rhSK42H6FqYX8eksgggImXZa9a1rfqD0uacBnP7SG0XhUyZ4dVHvYcu87ZvP70iCk02+eL3nl3Jj4gMbbXuz0NEujOkhEwE2ghGXd6q//Vmqt5mMW0/+xs7wytnHccqq2qmVVNXo2xVZcex6s9z0wggImncuKsHAuEflKY/QN8/+pLb/9VfrPwR0v+Gh0opn/2tmuE1VH37fk6ViKjbqimFNtcxqSwCiEhZ9pp1bcM/KE0iYiDCAdohRcTqoG2XGV5+OSXvV4nIuvaENkdE1hGb3nVEZHo2WWyNwj8oMSIS/uEaS0R8oy1VUEJbyJ54Iv6bMc99RGSedi2yVSkiEnoi/pIaU4AQN8Pr8a0pxYcOPV/sDK8qEWn6jwBjIlN4Q7vXARHpzpASMhFoIyL64xT+0ZKgTDUtYYZX29lZVfn1DpDKIoCIlGWvWdc2FJE2x4o50GB7CSllhpc8lHVreI3ddgl7aLO6OBHZijiRsS2W5/mISB6OlJKBQPgHKPa4JAEJMaXM8NKikOEaXmG5Yx2H3Yuyoc75EevqcqwTEOUnlUUAESnLXrOubaxoVOXTHyUFr5Wc5jAgL7Gosk+bcyXbcIl1R0SWaPWJtrnNH5q6vE0R0hNtdmW1ShaU2FV8q/JNeVyr0lCcdIgIL8FkCITC0DSzR33q6hap6j5pum8yjW1RkbYzvA4efG70GV5VAuHb19Y6889pX5MlSGURQETKstesaxv+QYkRg6pponPxRkJjt53hpdWHx5wyLPtpVQF//EPH/vhIaHNEJLT69I8RkenbaDE1DP+gxIiI4IT3LeEPkWZ4yUM5//wnt2JMmpasV74pzvBaou3m9g8aEZmbRQtuT/gHJUZEFBEd3rcEEfHNrBlemrGl1YObhMSu6SuNMZ/99Z8Rsy97qXtR/BUDIo+jadp11SD8XL3IGH6l5kFESrXcDOsdisE6EdEfoarPq05h6ZOxzJMyIC+PJkeq6lqUTTX+oWuWJPx103yntuKA1ZltPQFEpJ4NVwYmEIpI6rH/B2vgJkzqcSmCYp/9TW1IlajH2lFjJ6TyCCAi5dlstjWO/WPTlG/JXkjTiyFxUDeWdWmt22qGl0SobZL32GSfpmv+gHvb55J/PAKIyHjseXJAoOkPTMw1+tMDoDWHbacMt53hJTHwZ2Sts53yIiA1xirgNCJSgJGWUsV1f2yqrmsQV+LRNIC7FH5t26m1uFJmeGlm2Lpk4x6a0lvVxaUBeF3TGMi65eLXPYvr4xJARMblz9MhMAkCNsMrdspwXzO8JgGDSrQigIi0wkVmCMyfgMZC1IW1btzErktQ5NFMdVHI+Vts3BYiIuPy5+kQmDSBMWZ4TRoIlVshgIisIOEEBCBQRUAzvA4ceCbaQ1HelBleVc/m3HQJICLTtQ01g8BkCfQ9w2uyDadiKwQQkRUknIAABGIJ2AyvvXufivJQtDSLxltiZnjF1oF84xJARMblz9MhMBsCKZ/97WMNr9kALaQhiEghhqKaECiJQMpnf5nhVZKFt+uKiGyzYA8CEOiBADO8eoA6oSIRkQkZg6pAYO4E+hYUxlqGf4MQkeGZ80QIQMC5zQDFNotCxqzhpWnFKpM0HAFEZDjWPAkCEKgg0Pazv3UzvFSOfZgLIakA3dMpRKQnsBQLAQi0J5Ayw0seik01tqVYtEVI2vNPuQMRSaHGPRCAQO8E2s7wMi8EIendNDsegIjswMEBBCAwRQJtB+QRkuGsiIgMx5onQQACGQikCIq+1EjqhwAi0g9XSoUABAYg0GYNL42dkPITQETyM6VECEBgQAIajPe7r5r2EZL8hkFE8jOlRAhAYEACWn+rSTjCa8pPykcAEcnHkpIgAIERCFR90lcztbSysIIP5X1IOPQ9FHktmg5MykcAEcnHkpIgAIGBCSjAEJEYGHrwOEQkAMIhBCAAAQjEE0BE4lmREwIQgAAEAgKISACEQwhAAAIQiCeAiMSzIicEIAABCAQEEJEACIcQgAAEIBBPABGJZ0VOCEAAAhAICCAiARAOIQABCEAgngAiEs+KnBCAAAQgEBBARAIgHEIAAhCAQDwBRCSeFTkhAAEIQCAggIgEQDiEAAQgAIF4AohIPCtyQgACEIBAQAARCYBwCAEIQAAC8QQQkXhW5IQABCAAgYAAIhIA4RACEIAABOIJICLxrMgJAQhAAAIBAUQkAMIhBCAAAQjEE0BE4lmREwIQgAAEAgKISACEQwhAAAIQiCeAiMSzIicEIAABCAQEEJEACIcQgAAEIBBPABGJZ0VOCEAAAhAICCAiARAOIQABCEAgngAiEs+KnBCAAAQgEBBARAIgHEIAAhCAQDwBRCSeFTkhAAEIQCAggIgEQDiEAAQgAIF4AohIPCtyQgACEIBAQAARCYBwCAEIQAAC8QQQkXhW5IQABCAAgYAAIhIA4RACEIAABOIJICLxrMgJAQhAAAIBAUQkAMIhBCAAAQjEE0BE4lmREwIQgAAEAgKISACEQwhAAAIQiCeAiMSzIicEIAABCAQEEJEACIcQgAAEIBBP4P8Bm1TTHNmSbToAAAAASUVORK5CYII=[/img]
[b][color=#38761d]Prosedur Menghitung Jarak Titik ke Garis[/color][/b][br]Adapun langkah-langkah untuk menghitung jarak titik A ke garis [i]g[/i] dengan bantuan titik B, C, dan D sebagai berikut.[br][list][*]Menghubungkan titik A ke titik C dan titik D sehingga terbentuk segitiga ACD seperti gambar di bawah.[/*][/list][img width=699,height=366]https://i2.wp.com/bintangsekolahindonesia.com/wp-content/uploads/2021/03/segitiga-300x157.jpg[/img][br][list][*]Kemudian, menghitung jarak antar dua titik, yaitu AC, AD, dan CD untuk menetapkan jenis segitiga.[/*][*]Terakhir yakni, menghitung tinggi segitiga ACD, yaitu AB yang merupakan jarak titik A ke garis g.[/*][/list]
[b][color=#ff0000][u]Contoh[/u][/color][/b][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik A ke rusuk HG adalah….[br]Langkah penyelesaian[br][list=1][*]Gambarlah kubus ABCD.EFGH[/*][*]Hubungkan titik A dengan titik G dan H sehingga membentuk segitiga AGH.[/*][*]Tetapkan jenis segitiga yang terbentuk[/*][/list]
[b][color=#9900ff]Pembahasan[/color][/b][br]Perhatikan segitiga AHG siku-siku di H.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAbEAAAFmCAYAAADj66QmAAAgAElEQVR4Ae2dCZRdZZWoXf3aXtq9QGlsUBu6gYBEowvWauG91Q02rkxQIUDj6/YJomBLAw0mDEEGQyAoBBATEEEmmWxlVISYARIIc+YQMjEkqYTKXEOSGlJz3f3Wf27OrXOnutMZ/uG7axV1c+8Z9v72/9+Pc+6ucz4hPCAAAQhAAAKGEviEoXETNgQgAAEIQECQGIMAAhCAAASMJYDEjC0dgUMAAhCAABJjDEAAAhCAgLEEkJixpSNwCEAAAhBAYowBCEAAAhAwlgASM7Z0BA4BCEAAAkiMMQABCEAAAsYSQGLGlo7AIQABCEAAiTEGIAABCEDAWAJIzNjSETgEIAABCCAxxgAEIAABCBhLAIkZWzoChwAEIAABJMYYgAAEIAABYwkgMWNLR+AQgAAEIIDEGAMQgAAEIGAsASRmbOkIHAIQgAAEkBhjAAIQgAAEjCWAxIwtHYFDAAIQgAASYwxAAAIQgICxBJCYsaUjcAhAAAIQQGKMAQhAAAIQMJYAEjO2dAQOAQhAAAJIjDEAAQhAAALGEkBixpaOwCEAAQhAAIkxBiAAAQhAwFgCSMzY0hE4BCAAAQggMcYABCAAAQgYSwCJGVs6AocABCAAASTGGIAABCAAAWMJIDFjS0fgEIAABCCAxBgDEIAABCBgLAEkZmzpCBwCEIAABJAYYwACEIAABIwlgMSMLR2BQwACEIAAEmMMQAACEICAsQSQmLGlI3AIQAACEEBijAEIQAACEDCWABIztnQEDgEIQAACSIwxAAEIQAACxhJAYsaWjsAhAAEIQACJMQYgAAEIQMBYAkjM2NIROAQgAAEIIDHGAAQgAAEIGEsAiRlbOgKHAAQgAAEkxhiAAAQgAAFjCSAxY0tH4BCAAAQggMQYAxCAAAQgYCwBJGZs6QgcAhCAAASQGGMAAhCAAASMJYDEjC0dgUMAAhCAABJjDEAAAhCAgLEEkJixpSNwCEAAAhBAYowBCEAAAhAwlgASM7Z0BA4BCEAAAkiMMQABCEAAAsYSQGLGli6+wO+7T2TqVJGurvx91teLnHuuyPLl+e/xCgRcJKDmiZov48cP/qg5ouYKj/AJILHwmVq3RSRmXUlJKCIC6n/mlLxefDF7B+rfhV7PXop/VUMAiVVDzbF1kJhjBSfdqgiUOiuhRHbJJSJ79lS1eVYqQgCJFQHDy4MEkNggC55BoBgBJalip93VOkpyai4hsWIEq3sdiVXHzam1kJhT5SbZKgj434PlnkasYlOsUiEBJFYhMBcXVxILfkld6DmNHS6ODHL2CaijK3WqEIn5ROL7jcTiY23snjgSM7Z0BB4TgWIS8xs9gv/jh+jCLQoSC5enlVtDYlaWlaRCJFDO6cRiogsxDCc3hcScLHtlSSOxynixtJsEhponiggSi2ZcILFouFq11aEmZ6m2YqtAkAwEhiBQai4gsSHg1fAWEqsBniurIjFXKk2etRLwvwNTcyb48F/n78SCVMJ5jsTC4Wj1VpCY1eUluZAJ+N+PBZs51HM6eEMGvX9zSCwarmwVAhCAAARiIIDEYoDMLiAAAQhAIBoCSCwarmwVAhCAAARiIIDEYoDMLiAAAQhAIBoCSCwarkZt9YEHHpBTThktX/jCkXLUUV+RCy64QN555x2jciBYCERN4MEHH5RvfnPM/nnyZTn//PPlrbfeinq3bL8EASRWApDNb+/du1e+8Y0xMnz4ODnhhBdk5MjNcsopa2TEiOly4IF/J7fddpvN6ZMbBMoi0NbWJqeccqoMH14nJ5zwJxk5ctP+eTJDPvOZQ2TatGllbYeFoiGAxKLhasRWTz31DBk+/OqCF/cdNepjOfTQL8vjjz9uRC4ECYGoCNTVnSXDh08qMk8a5POfHyGPPvpoVLtnuyUIILESgGx9+4UXXpAjj/w/BSem//ct//zPC+Qf/uFoWxGQFwRKEpg5c6YceeSJJebJ63L44UeV3BYLREMAiUXDVfutXnzxxfLVr9495ORUMjv4oH+Uy84/UW67dlTVP49NO09W/X4GPzAwbgx8e/S/yIgRM0rOk8MPP14WL16s/by3MUAkZmNVy8hp5MjxcuKJM0tOzi8eerJ8539/RqaeeUjVPzefeYg8c9HJMmdiHT8wMGoM/NMRR8qJJ75Qcp4MG3amPP/882XMPBYJmwASC5uoIds755zz5PjjHyk5OQ85eLhcOOZwufW8Y6v6uebfvyDXf/vv5bkr6+SVn5zDDwyMGgOjv3a0HHfcwyXnyZFHniQLFiwwZPbbFSYSs6ueZWfz0EMPyYgRZw85OUeO3Cif+tRfy0frl8nG+ncr/pm9+FkZefu/St0vRsuS1a/Kvqbt/MDAqDHw67uny1e+fEaJeVLvzZOenp6y5x8LhkcAiYXH0rgtHX30CDn++EeLTtBhw8bLhIkXVSwvX3hIDGnb8D8uRxx2xJBnLY455myZMmWKcfPfloCRmC2VrCKPRYsWyUEHHSrDh98kY8c2Z2R20kkL5YgjRslpp51etcCUyHSUWGfLTuna2yydzTuMOiKwQQYm5rBl4Usy4/+eKAd++gA59tgbZOzYpsA8WSTDhp0mZ599ThWzj1XCIoDEwiJp6HY2b97sXaHjk5/8K/mbT/+tfOqv/loOP+wImXzDpJoEFqbElHT6e7okNTCQppxKyUB/n/R2tktnyy5PRl17mqSvu1NSA/2ZSqT6+6Wvs0M6d++S7tbdMtAXPN2Tkv6ebk9oJn64EnP0R7lN7y+Xedf8u8y+7FR54oej5D9OG+WdNjzooMPlgAM+J0cc8SWZPn16ZrzxJBkCSCwZ7trt9YkHr5QrxxwsV405SNZ/sKhmgYUlsZ72vaJktLN1pwyfPFw+8cNPeD8X//Zij6GSW3fbHhno65WO7g6pu7sus4x6rl5T8lLSC25DbUv9u7+3W7p2N3JUxnd1WWOgfcfH8ua0S2TWZWNl7uXj5f0/PZyZs5s2bZIdO3Zk/s2TZAkgsWT5a7N3JbGbzzpEbhx/sDYSU0dgSk6+fHxxKWjquffvVEpS/X0ZgfnL+ELz/+2vM3fNXI+5+q3eU0d3SpQc2UR/ZGMS46W/vkFmXTpG5lx+urz7KJeV0uaDqkAgSKwAFBdfqkRiDQ1rpbW1Sfr6ejOo1POurg7p6+uRnp5OaWz8OOs7sVUfLZK+rn3S39sjAwV+1Ou96tTf/tOD6gOvt6NNUqmU3D3/bu8oTMnMf/hiC0rpc5d/TlY2rPQX8Z4fO/nYzGtKWunlU95vT3CplPTua0NiHIllxsDqJ++WWZeOljkTx8nC6Vd6/5OTGVQ80Y4AEtOuJMkEVK7Etmx5X/Z1topIyjuS8U/vqVN3Gxs3erJR0unu3icL1y3wWuwvfOQC2dPaVDqxVMr7XkuJTDVeKOmph5KNJxwR78hMnRr0j7TUvtRD/c6cPuzv874by13GF5+K2T+dyJEYR2DBI8T1c36XFtiEOnn1hvNkb8N6b3zxH30JIDF9axNrZOVIbNPm92Rva6OkUgOeVHwRqECVRNRRjzoaUkc7AwP9su7jlZ7Eps/9ufT29Xiv+9Ir9Ntbr79Puvd3D6pGDfXISExJrrPDa/LwBeXLLbOMSPqIr6c7Izp/mUJA1REg34khMiWyLQtf9gQ2+0enydwrxsvO97gdUaE5o9trSEy3iiQUTzkS27rtQ+8IS52y82Xlh+tLxT+l19vbLUs+eMOT2DXPTJKOzjZ/0SF/e40We5q8Uzv+kZgSZEaYqZRIKpX3PVlGYsVEp74787sb90eg9qWEGfw/cZ67KbSmD1ZkOhGVwDa//sKQ45Q39SGAxPSpRaKRlCOxXbs2S39/r3dE5UtFHXF1d3d4310pkfivd3a2yevvzc1csWPrrnpvmaGSzD2153UmDgx432kpOQaPqNRzdTTnv6Z+e8/Vd1zqaK27M/tIzHu9XVQrvtquartHWG4KK7fu7TsainYiDjVeeU8PAkhMjzokHkU5Emtq2iL9/X1ZjRY9PV2yZ+8u7xSj/71Ue1e7tLU1y8vLnvckduvMn0p3T1dZOapuRCUa9UGjRKNa6NXDP/rzT0M+t/w57zuwQhLr6ypwypEGDqRdpHmFTsSypqa2CyExbUsTb2DlSKyx6WNPYuq7K/+Iq6e3y+tUzP6ebIe0t+/OSOyOWdMq+k5MtdZ7EmvZ6TV6FCLhN2kocaqHL1B1WlMdhanvuvxTnOo9FV9PRysf5EU+yHOPTlz59+onf0knYqEJZtBrSMygYkUZajkS27Fzo9dC7x8VKZkpOaijM18Y/ndiqt3+jVUveUdi37rnDNnZ3OB9lzVUDup0Ym9ANOkW+4GsIz9/fbVvf1/qteC/VUzqezMVp99ir67koa7a4cqHM3mWPlW6fu7vBzsRp5wnrXQi+tPLqN9IzKhyRRdsORJr2LJOOjvbvSDUaTy/pV29oI52/FN9Sijq78WWf/R25jux5Wtf976LUt9XqQ7D3B91CanutmzJ5H4n5h91+Udh/qlE9bdkvkT9mPx/+8uoS0x1cmUOJL7/SHTLIjoRo/s0iXfLSCxe3trurRyJqUtJNbdslf6BPi8PJQhfXLl/J6aOzlbXL8tIrJpbsajWd3VaUD38oz9/f77Q1BGW6jJUR16+uPxlfKHlNoxwlFL6KMVmRulOxP/wrolIJ6K2H0llB4bEykZl94LlSsz7W7G9jd7fgRUjoo6M2jt2y6vv/rkmiakP0u7WFu8PnAvtSwlMnX70GkC8vylL5S2mTi16Fwpu5qr1Noup3NzadzbIm7f9d+aaiB8EromYN3h4wQgCSMyIMkUfZLkSU0dj6mfnrk3SsW+v9PZ2eT/79rXK3r27vKt5KIFt2/5R1mWnqjkS8z+Y1O1TlIjU5arUdRJVB6P6GzK/i9Ffrqe91TsqUxcMVsv0d3fxPRiNHFmnUJfeP4VrIkb/cRLrHpBYrLj13VlQYnf98Wa5a+a0UH64s7Pbp+78/8HQ4ffqpwKdiDO4JqK+n0aVRYbEKuNl7dK+xG4af7CMvfUbMur2U0L7qfvFaKnlSEyHD0BiMFvG2Z2I36MT0aJPMiRmUTFrSWXl7Mdk2rcOk6ln/p2Mv2OkKPGE9fNfD58vWz5em3VaBymYLQWT6rc1txNxFddErOWzQrd1kZhuFUkonk0Lnpc5l4/z/m6mbWs9wuG7JCvGQLO6JuK1dCIm9LESy26RWCyY9d8JEuPIyKSjq3Jize9E/I3+E5EIKyaAxCpGZucKSAyJlSMGk5bJ6kR87DY7Jy5ZCRJjEHgEkBgSM0lQpWJdk9WJeJWoP7/gYScBJGZnXSvOCokhsVJiMOX9DXOfzFwTccGU70nrFu7OXPEHgkErIDGDihVlqEgMiZkiqaHi3LponiewzN2ZVy2MctqwbQ0IIDENiqBDCEgMiQ0lBxPea/7gXZmf1Yn4og5TixgiJoDEIgZsyuaRGBIzQVTFYlSdiG9lXRORTkRTPntqjROJ1UrQkvWRGBIrJggTXl92/42D10SkE9GST6Xy0kBi5XGyfikkhsRMkFWhGNc8dU+6kWPiOFk44yrvDt7WT1gSzBBAYhkUbj9BYkiskCB0f23DS7mdiBvcnsgOZo/EHCx6oZSRGBLTXVi58W1dnN2JuItOxEJT2/rXkJj1JS4vQSSGxHIlofO/mz9UnYjfDtydmU7E8ma6fUshMftqWlVGSAyJ6SytYGzpTsRLB+/O/AKdiFVNektWQmKWFLLWNJAYEguKQufnyx6gE7HW+W7T+kjMpmrWkAsSQ2I6i8uPbc3T2Z2IvR1tNYx6VrWBABKzoYoh5IDEkJgvCl1/04kYwkS3cBNIzMKiVpMSEkNiuspLxUUnYjWz2o11kJgbdS6ZJRJDYrpKzOtEvC7QifgGnYglJ7RDCyAxh4o9VKpIDInpKDGvE/F2OhGHmruuv4fEXB8B+/NHYkhMR4kFOxFXck1EPq0KEEBiBaC4+BISQ2K6SSy7E3GS9O6jE9HFz6ZSOSOxUoQceR+JITGdJLbhpacG78584/eldQvXRHTko6jiNJFYxcjsXAGJITFdJLZ18fysuzNzTUQ7P3PCygqJhUXS8O0gMSSmg8ToRDT8gySB8JFYAtB13CUSQ2JJSyzdiXhZ4JqIj+g4VYhJMwJITLOCJBUOEkNiSUts2QM3Ze7OvPKx25OaCuzXMAJIzLCCRRUuEkNiSUpszdO/Grw7812qE7E9qqHOdi0jgMQsK2i16SAxJJaUxPI6EbdurHYYs56DBJCYg0UvlDISQ2JJSGzrkpxOxNWLCg1PXoNAUQJIrCgat95AYkgsbomlOxH/3+Ddmd+Y6dakI9tQCCCxUDCavxEkhsTilFjHzgZ563Y6Ec3/5Eg+AySWfA20iACJIbE4JZbVifg4nYhafAgYGgQSM7RwYYeNxJBYXBJb80xOJ2InnYhhz2eXtofEXKr2ELkiMSQWh8Q2vJxzTUQ6EYeYlbxVDgEkVg4lB5ZBYkgsaoltXfJK9jUR6UR04JMl+hSRWPSMjdgDEkNiUUqs+cOVMv/6wU7Ej+lENOJzwYQgkZgJVYohRiSGxKKSmNeJeAediDFMYyd3gcScLHt+0kgMiUUlsWUPBq6JSCdi/uTjlZoIILGa8NmzMhJDYlFIbM0z92auibjorknS19lhz6QhEy0IIDEtypB8EEgMiYUtsY0vP50W2IQ6WXDj96Vta33yA50IrCOAxKwraXUJITEkFqbEttGJWN1EZK2KCSCxipHZuQISQ2JhSSzdifidzDUR6US08zNDl6yQmC6VSDgOJIbEwpBYx84t8tYdPxq8O/OL3J054alt/e6RmPUlLi9BJIbEwpDY8genDt6dmU7E8iYfS9VEAInVhM+elZEYEqtVYmuzOhGvlr4uOhHt+YTQNxMkpm9tYo0MiSGxWiSW1Yl40/nSto1OxFgnsMM7Q2IOFz+YOhJDYtVKjE7E4EziedwEkFjcxDXdHxJDYtVITHUivnJ9oBPxTe7OrOkUtzYsJGZtaStLDIkhsUolpjoR387qRHy0skHH0hAIgQASCwGiDZtAYkisUolldyLeYcM0IAcDCSAxA4sWRchIDIlVIrH8TsR9UQxLtgmBkgSQWElEbiyAxJBYuRLbOC9wTUSvE3GTG5OELLUkgMS0LEv8QSExJFaOxPI6Edcsjn+wskcIBAggsQAMl58iMSRWSmL5nYh/dnnKkLsmBJCYJoVIOgwkhsSGkpjXifjzwWsifvginYhJz1n2nyaAxBgJHgEkhsSGktjyh24OXBORTkQ+NvQhgMT0qUWikSAxJFZMYmufvW/w7sx3q2sidiY6Vtk5BIIEkFiQhsPPkRgSKySxjfOeGbw7s+pE3E4nosMfE1qmjsS0LEv8QSExJJYrsXQn4hiZ/aPTZO4V42UXnYjxT0z2WJIAEiuJyI0FkBgSC0rM60T8yTmDd2d+k05ENz4JzMsSiZlXs0giRmJIzJdYx64t8vbPJ2TuzkwnYiRTjo2GRACJhQTS9M0gMSTmSyyrE/EJOhFNn9u2x4/EbK9wmfkhMSSmJJbXidhNJ2KZU4jFEiKAxBICr9tukRgSC3YivnbT+dK+fbNuw5R4IJBHAInlIXHzBSTmtsRyOxEb1yxxcyKQtXEEkJhxJYsmYCTmrsSaP1opr9CJGM3EYquRE0BikSM2YwdIzE2J5XUizuSaiGbMWKL0CSAxn4Tjv5GYmxKjE9HxiW9B+kjMgiKGkQISc09i2Z2IP5b+7q4whhLbgECsBJBYrLj13RkSc0ti2Z2IF0j7DjoR9Z2dRDYUASQ2FB2H3kNi7kgsrxNxLZ2IDk1161JFYtaVtLqEkJgbEsvvRJxV3YBhLQhoQgCJaVKIpMNAYvZLLN2JOHHwmogzH0t62LF/CNRMAInVjNCODSAx+yW2/OGfDt6d+Ymf2zFwycJ5AkjM+SGQBoDE7JbY2ud+Hbg784+lv4dORKa+HQSQmB11rDkLJGavxDbOezZzd+bXpqpOxI9rHi9sAAK6EEBiulQi4TiQmJ0S27b0Fe87MP/uzI1rlyY80tg9BMIlgMTC5Wns1pCYfRLzOhEnnzt4d+a36EQ0doISeFECSKwoGrfeQGJ2SczrRLyTTkS3ZrGb2SIxN+uelzUSs0tiwU7E9+hEzBvvvGAPASRmTy1rygSJ2SOx/E7E7prGBitDQGcCSEzn6sQYGxKzQ2Ib5+d2IjbEOIrYFQTiJ4DE4meu5R6RmPkS27b01exOxHV0Imo52QgqVAJILFSc5m4MiZktsdxOxAY6Ec2djEReEQEkVhEuexdGYuZKTHUivkMnor2Tk8yGJIDEhsTjzptIzFyJrQhcE5FORHfmLJmmCSAxRoJHAImZKbF1z90/eE3EX/5Y+nvpRGRKu0UAiblV76LZIjHzJJbXibiTTsSiA5w3rCWAxKwtbWWJITGzJKY6EWdfNlb8ayI2rVtWWcFZGgKWEEBilhSy1jSQmDkSa/7oPXl18ncz10RseGt2reVnfQgYSwCJGVu6cANHYmZIrGPXVnnnzsu5O3O4w5+tGUwAiRlcvDBDR2JmSGzFwz9L35154uny3m/vDHMIsC0IGEkAiRlZtvCDRmL6S2zdH4KdiNfIQG9P+AOBLULAMAJIzLCCRRUuEtNbYtmdiD+Qjp1bohoKbBcCRhFAYkaVK7pgkZi+Ekt3Ip462In4/vLoBgJbhoBhBJCYYQWLKlwkpqfEvE7EGwKdiG/TiRjVHGC7ZhJAYmbWLfSokZh+EvM6EX8R6ET88+Oh150NQsB0AkjM9AqGFD8S009iK35DJ2JIw5vNWEwAiVlc3EpSQ2J6SSzYibj4l9fIQB+diJWMZ5Z1hwASc6fWQ2aKxPSRWF4n4i46EYccvLzpNAEk5nT5B5NHYnpIzOtE/BGdiIMjk2cQGJoAEhuajzPvIrHkJdairomY1Yk4x5nxR6IQqJYAEquWnGXrIbFkJUYnomUTinRiI4DEYkOt946QWLISW/GbW7gmot5ThOg0JYDENC1M3GEhseQklt+J2Bt3+dkfBIwlgMSMLV24gSOxZCSW1Yl48w9EnVbkAQEIlE8AiZXPyuolkVj8Ekt3Ip42eE3ED1ZYPcZIDgJREEBiUVA1cJtILF6JpTsRzxu8O/M7cw0cNYQMgeQJILHka6BFBEgsPomlOxGvyNyd+SOuiajFHCAIMwkgMTPrFnrUSCw+idGJGPrwZYMOE0BiDhc/mDoSi0diWZ2I96hrItKJGByHPIdApQSQWKXELF0eiUUvsfr5z8qsS0fLnAl18trN/ykdjXQiWjqdSCtGAkgsRtg67wqJRSux7E7EM6SJTkSdpwOxGUQAiRlUrChDRWLRSSy3E3ELnYhRDmW27RgBJOZYwYuli8SikZjXiTg90Ik464liJeB1CECgCgJIrApoNq6CxKKR2IpHgtdE/IWNQ4ecIJAoASSWKH59do7EwpdYdifitTLQ36dPwYkEApYQQGKWFLLWNJBYuBILdiK+fvN/yr7GbbWWiPUhAIECBJBYASguvoTEwpOY14k4wb8m4hnS/MG7Lg4pcoZALASQWCyY9d8JEgtHYl4n4pTBayJuWfiS/sUnQggYTACJGVy8MENHYrVLLN2JeOXgNRHpRAxziLItCBQkgMQKYnHvRSRWu8RWPHLr4N2Z/4dORPdmERknQQCJJUFdw30isdoktu4PD6QvKTVxnCy+51pJ9fdrWGVCgoB9BJCYfTWtKiMkVr3E8joRm+hErGoQshIEqiCAxKqAZuMqSKw6iaU7EevSd2e+8gxp/pBORBvnBznpSwCJ6VubWCNDYpVLTHUiLpjyvczdmelEjHXIsjMIeASQGAPBI4DEKpOYuo3KwunBTsTfMpIgAIEECCCxBKDruEskVpnE3qUTUcdhTEwOEkBiDha9UMpIrHyJ5XUiDtCJWGhM8RoE4iCAxOKgbMA+kFh5Equf/1zm7szeNRGbthtQXUKEgL0EkJi9ta0oMyRWWmLbli6QOROCnYgrK2LMwhCAQPgEkFj4TI3cIhIbWmIt63M6ERe9bGSdCRoCthFAYrZVtMp8kFhxieV1Is7+nyopsxoEIBA2ASQWNlFDt4fEikss2Im4imsiGjrCCdtWAkjM1spWmBcSKyyx/E7EgQrJsjgEIBAlASQWJV2Dto3E8iWW1Yn40x/KvqYdBlWUUCHgBgEk5kadS2aJxLIltm3ZApkz0e9EPFOaP6ITseQgYgEIJEAAiSUAXcddIrFBibWsXyULbvz+4DUR6UTUccgSEwQ8AkiMgeARQGJpiXmdiDOuytydeT2diMwQCGhNAIlpXZ74gkNiaYlldSL+bnp8BWBPEIBAVQSQWFXY7FsJiW2XrE7EX10nqRSdiPaNdDKyjQASs62iVebjusTyOhGb6USsciixGgRiJYDEYsWt785clli6E3Gcd3fml648U9TNLnlAAAJmEEBiZtQp8ihdlVhuJ+LWRfMiZ80OIACB8AggsfBYGr0lFyXW0bhNFgY7Eef8zugaEjwEXCSAxFyseoGcXZRYdifijAJUeAkCENCdABLTvUIxxeeaxHI7ESWViok0u4EABMIkgMTCpGnwtlySWP0rgbsz//SH0tm80+DKEToE3CaAxNyufyZ7VySW14m4nk7EzCDgCQQMJIDEDCxaFCG7ILG8TsTFdCJGMZbYJgTiJIDE4qSt8b5slxidiBoPPkKDQA0EkFgN8Gxa1XaJ0Ylo02glFwgMEkBigyycfmazxNb98QGZdelomTNxnCz+1XVCJ6LTQ53kLSOAxCwraLXp2CqxvE7EFjoRqx0jrAcBHQkgMR2rkkBMNkos3Yl4evqaiFedKaqxgwcEIGAXASRmVz2rzsY2iXmdiDedn7k789bF86tmw4oQgIC+BJCYvrWJNTKrJJZ7TcS5v4+VJTuDAATiI4DE4mOt9Z5skmk8qdAAAApNSURBVNi7j94qsy4dI3Mmni6rfn+X1twJDgIQqI0AEquNnzVr2yKxYCfiEtWJyAMCELCaABKzurzlJ2eDxLI7ES+UzpZd5QNgSQhAwEgCSMzIsoUftOkS8zoRL/c7Ec+SlvWrw4fEFiEAAe0IIDHtSpJMQCZLLK8TcQmdiMmMIvYKgfgJILH4mWu5R2Ml5nUiTpJZl42VuZePlw10Imo5vggKAlERQGJRkTVsu6ZKLNiJuJpORMNGHeFCoHYCSKx2hlZswUSJZXUi3nu9FXUgCQhAoDICSKwyXtYubZrEsjoRf3ahdO6mE9HawUliEBiCABIbAo5Lb5kkMdWJODfYibiBTkSXxiq5QiBIAIkFaTj83BSJqU7E1wLXRNy25BWHq0bqEIAAEmMMeASMkJjqRLwr2In4JNWDAAQcJ4DEHB8AfvomSOzdR6dlrom4+sm7/dD5DQEIOEwAiTlc/GDqukts3R8fzNydecm9PwmGznMIQMBhAkjM4eIHU9dZYrmdiF27G4Oh8xwCEHCYABJzuPjB1HWV2HavE3H8/rsznyW7N6wJhs1zCEDAcQJIzPEB4Kevo8TSnYgXZO7OvG3pq364/IYABCDgEUBiDASPgHYSy+1EfIlORIYqBCCQTwCJ5TNx8hXdJEYnopPDkKQhUDEBJFYxMjtX0ElidCLaOcbICgJREEBiUVA1cJu6SKz+lT+kW+kn1MkbP7tQuvbQiWjgcCJkCMRGAInFhlrvHekgMa8T8YpAJ+JGOhH1HjVEB4HkCSCx5GugRQRJS8zrRJxKJ6IWg4EgIGAQASRmULGiDDVRieV1Ij4VZapsGwIQsIgAErOomLWkkqTEsjoRn/plLWmwLgQg4BgBJOZYwYulm5TE3g9eE/G+ycXC43UIQAACBQkgsYJY3HsxCYlldyL+l3TtaXIPPBlDAAI1EUBiNeGzZ+W4JbZ92Wsy1+9EnPRvsnvjWntgkgkEIBAbASQWG2q9dxSnxPI6EZct0BsO0UEAAtoSQGLalibewOKTWM7dmV9+Ot5E2RsEIGAVASRmVTmrTyYuiQU7EdfQiVh9wVgTAhDwCCAxBoJHIA6JBTsRl9KJyMiDAARCIIDEQoBowyaillhWJ+ItdCLaMGbIAQI6EEBiOlRBgxiilFi6E/GM9N2ZVSdiPZ2IGpScECBgBQEkZkUZa08iKom1rF8trwWviUgnYu3FYgsQgECGABLLoHD7SVQSW3jXJJl12ViZe/l42UgnotuDjOwhEAEBJBYBVBM3GYXEsjoRn77HRCzEDAEIaE4AiWleoLjCC1tiWZ2Iv74hrjTYDwQg4BgBJOZYwYulG6bEsjsRL5Kuvc3FdsvrEIAABGoigMRqwmfPyqUk1rW7Ufq7O0VSKS/pgb4+6WnbI/uatmf95HYi7qlfZw8kMoEABLQjgMS0K0kyAQ0lsc7mHdLXtU+6ukSmThUZP15k+XKRgb5e78rzvshaNmR3Iiqh8YAABCAQJQEkFiVdg7Y9lMTULVKUsOrrRa6+Oi0yJbPOzpT0drRljsQWBTsR5z1jUPaECgEImEoAiZlauZDjHkpivR2tkkoNyH33pQX29tsi554rntT6e7qlc/cuoRMx5IKwOQhAoCwCSKwsTPYvVExinS07pb+nS/bsEbnkEpEXX5Ss56mBftm+bIHMunS0zJk4TpbSiWj/YCFDCGhEAIlpVIwkQykmse7W3ZLq7/e+A/OPvlSc/lFZZ+eANLw9W+Zd/S1549aLpHtvS5JpsG8IQMAxAkjMsYIXS7eYxHo7272ORF9aqrlDPVRjh9/g0bZ9s3cEtmcTnYjF+PI6BCAQDQEkFg1X47ZaSGJeQ0dvj/fdlzoKU+LyH36nopJbf3eXtG3f5L/FbwhAAAKxEUBisaHWe0eFJNbTvldSAwPe92DqqKvQj/qeTH1fxgMCEIBAEgSQWBLUNdxnrsS8vw3r7sz8bZg64sp9qJb73CO03GX4NwQgAIEoCSCxKOkatO1ciXXvbZaB/r6CpxL9tPxTiupvxvzvyvz3+A0BCEAgDgJILA7KBuwjV2K9+9oyDR3+KcPefe2y5N7rvU7E7Sve8LJSLffBrkUDUiVECEDAIgJIzKJi1pJKUGLt2zZLX3dn5u/B/FOJO1e9I/Ov/468POls7yodan/+KUUlMx4QgAAE4iaAxOImrun+ghJr21ov3a0t3ulEP1zV5LHm6Xtk7hXjZfvy1/2X+Q0BCEAgUQJILFH8+uw8V2Lqor49Ha3S39stLetXy9L7b0zfnXn+s/oETSQQgIDzBJCY80MgDaCQxJTIsq6J+My90IIABCCgFQEkplU5kgumkMSCd2dedv+U5IJjzxCAAASKEEBiRcC49HJPT4/ce9PV8oOThstFJx8r8/70rNS/+of0RX0n1Mmbt14s6hqKPCAAAQjoRgCJ6VaRmOO5//775cADD5IvHTVKjj1monzpqAvki58/Vr52+Bflge+eLC9ffbbs2fRBzFGxOwhAAALlEUBi5XGycqkZM2bIoYeOkJNPXpp3SakRI2bIZ//ms7Jw5pNW5k5SEICAHQSQmB11rDiL9evXy1/+5Sflm9/8ME9g/jUSv/KVW+Wss75V8bZZAQIQgEBcBJBYXKQ128/UqVPl6KOvKiowX2QHHPC30tDQoFn0hAMBCEAgTQCJOToSTj/9bPn6158rKbFhw8bInDlzHKVE2hCAgO4EkJjuFYoovrq6f5Ovf/2PZUjsVJk1a1ZEUbBZCEAAArURQGK18TN27cmTJ8sxx1xbUmKf/eyhUq8ukMgDAhCAgIYEkJiGRYkjpDVr1sinP32gjBrVUFRkqkNx7NhxcYTDPiAAAQhURQCJVYXNjpVuueUWOeywEwt2KB533MOimjqU7HhAAAIQ0JUAEtO1MjHFdeedd8pf/MX/kq997buiWuq/+tWfyLBhJ8lxx50gS5YsiSkKdgMBCECgOgJIrDpuVq3V2NgoDz30kFx33XWiWu9nz55tVX4kAwEI2EsAidlbWzKDAAQgYD0BJGZ9iUkQAhCAgL0EkJi9tSUzCEAAAtYTQGLWl5gEIQABCNhLAInZW1sygwAEIGA9ASRmfYlJEAIQgIC9BJCYvbUlMwhAAALWE0Bi1peYBCEAAQjYSwCJ2VtbMoMABCBgPQEkZn2JSRACEICAvQSQmL21JTMIQAAC1hNAYtaXmAQhAAEI2EsAidlbWzKDAAQgYD0BJGZ9iUkQAhCAgL0EkJi9tSUzCEAAAtYTQGLWl5gEIQABCNhLAInZW1sygwAEIGA9ASRmfYlJEAIQgIC9BJCYvbUlMwhAAALWE0Bi1peYBCEAAQjYSwCJ2VtbMoMABCBgPQEkZn2JSRACEICAvQSQmL21JTMIQAAC1hNAYtaXmAQhAAEI2EsAidlbWzKDAAQgYD0BJGZ9iUkQAhCAgL0EkJi9tSUzCEAAAtYTQGLWl5gEIQABCNhLAInZW1sygwAEIGA9ASRmfYlJEAIQgIC9BJCYvbUlMwhAAALWE/j/Ug28yRO00P4AAAAASUVORK5CYII=[/img][br]Jarak titik A ke rusuk HG adalah panjang ruas garis AH, ([math]AH\perp HG[/math])[br][math]AH=6\sqrt{2}[/math], (AH diagonal sisi)[br]Jadi jarak A ke HG = [math]6\sqrt{2}[/math] cm[br][br][br][br]
[u][b][color=#ff0000]Contoh[/color][/b][/u][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik B ke diagonal AG adalah….[br]Langkah penyelesaian[br][list=1][*]Gambarlah kubus ABCD.EFGH[/*][*]Hubungkan titik B dengan titik A dan G sehingga membentuk segitiga ABG[/*][*]Tetapkan jenis segitiga yang terbentuk[/*][/list]
Lihat segitiga ABG[br][br][math]BG=6\sqrt{2}[/math], BG diagonal sisi[br][br][math]AG=6\sqrt{3}[/math], AG diagonal ruang
[b][color=#00ff00]Pembahasan[/color][/b][br]Perhatikan segitiga siku-siku ABG[br][math]L\Delta ABG=\frac{1}{2}\times AB\times BG[/math][br][math]L\Delta ABG=\frac{1}{2}\times AG\times BP[/math][br][math]L\Delta ABG=L\Delta ABG[/math][br][math]\frac{1}{2}\times AB\times BG=\frac{1}{2}\times AG\times BP[/math][br][math]AB\times BG=AG\times BP[/math][br][math]BP=\frac{AB\times BG}{AG}[/math][br][math]BP=\frac{6\times6\sqrt{2}}{6\sqrt{3}}[/math][br][math]BP=\frac{6\sqrt{2}}{\sqrt{3}}\times\frac{\sqrt{3}}{\sqrt{3}}[/math][br][math]BP=\frac{6\sqrt{6}}{3}[/math][br][math]BP=2\sqrt{6}[/math][br]Jadi jarak titik B ke AG adalah [math]2\sqrt{6}cm[/math].
[b][color=#ff0000]Contoh[/color][/b][br]Diketahui T.ABCD limas beraturan. Panjang rusuk alas 12 cm, dan panjang rusuk tegak [math]12\sqrt{2}[/math] cm. Jarak A ke CT adalah . . .[br]Langkah penyelesaian[br]1. Gambarlah limas T.ABCD[br]1. Hubungkan titik A dengan titik C dan T sehingga membentuk segitiga ACT[br]2. Tetapkan segitiga yang terbentuk
[b][color=#f1c232]Perhatikan segitiga sama sisi ACT[/color][/b]
[b][color=#00ff00]Pembahasan[/color][/b][br]Perhatikan [math]\Delta[/math]ACP[br][math]AC=12\sqrt{2}[/math][br][math]CP=\frac{1}{2}\times CT=\frac{1}{2}\times12\sqrt{2}=6\sqrt{2}[/math][br][math]AP=\sqrt{AC^2-CP^2}[/math][br][math]AP=\sqrt{\left(12\sqrt{2}\right)^2-\left(6\sqrt{2}\right)^2}[/math][br][math]AP=\sqrt{288-72}[/math][br][math]AP=\sqrt{216}[/math][br][math]AP=\sqrt{36\times6}[/math][br][math]AP=6\sqrt{6}[/math][br]Jadi, jarak titik A ke CT adalah [math]6\sqrt{6}[/math]cm.
[b][color=#9900ff]Jarak Titik ke Bidang[br][/color][/b][br]Garis tegak lurus Bidang[br][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARwAAAE1CAYAAAA1V18eAAAgAElEQVR4Ae3dB9gsNdk38P2wKwiIFGmHpoCUg6JYXqkqSJGionQEFQQEEelFAQFBelU/RJQmIkpTKaKIHj30XqSIBQVUioAV9c17/Rfv52SzyUzKnUwym3Nde2Umk2Rm95n8zp3M7M7gX//6l+jq9e9//1vU17/Ff/7zn/qy/Az+93//V9RXGZ+B0PwbdIUN7beC8zy6FR17dCs4ZYAj/53IngpOJlFWBaeCI3fQvi5XcCo4wcM5cdNAyK8UePa1Q/b9fQ2ee+45QS8a5vQ9ncRhXEwEZGywHHNfXG33vWPn+v4mEhyAOmnocHVUXTslgoP3kWun7PNxVXAyGVKlAFCHBUdeBae8SdyuUBsBB0Orvg+n6P2l6OC57YMDF10bpYKD99JVx5vU/VZwaoQTPOdSMjgVnbTR2cSCM4nzOIi4dBFKaF4FJ22nLTk6quBMUIRTwdHf61NyBy7t2Cs4FZzgqKf0CKcOq9JFaGPg1Injfn+/K3T4pKtfwUnXYUuLaNTjnWhw6jyOfoihQ6Uprw/g4P2pnaOu80NawZmwIVWMeZy+gFPR4QdGRVsLDn3VIWVK98f0Kc3tPpwYx4NO2idwmiK5pm1qx6rreryyAaePc0cxOniObVZw6nDMFtgKTuQfIMsRCO5jquA8Pxdm2+kmuVwFp4IT/EXWCs6syfdJxsTmvWcFTh1WlXlJvoIzC5w68ayfuyGMKjiRI5xJuPRewangEChtaQWnglOHVJY/4N50lUrd1tbxJnV7BaeCU8GJAE4dWumHVtmB08d5nL4Pq+qQanRIJUc7kxrJmN53BSdBhFPBMXdIuXP2cdnU8SY1f/DPf/5TuL5S3oEca1+l39HMfS9NSHtqhBPSVh/R8XlPfQXJCxwAFQuCVO1WcPguwXOCA6x8Omgf6/QRnQpOoiFVDOBCIgnOuhWceEPGvqEzseAgkoqBQMo2OdEIaYsbHBxLHyMW3/fUJ3S8wanDqn9lAVYIFFx1Y4BT0RmNmvqCTgWn4CEVoikuNELaqeCM4uAbydjUKx2eiQanDqt4Jo5jgVOjHD1kJaNTwSk8wskhyqng6GGwiVh8y5SKThA4fZjHqVFOeJQTE5wa5ZgxKxGdCk69WhU8DxQbnIpOf9AJBsf1LmWf8qluBuTYT8rL4pz7ynHSOOSYfIcqk1wvRcRUwXnuOfa7pjkhSNmWbwdPEeH4HNsk4xHy3mPCU8Gp4IzcT+TTsXMFB+8lpONNet0Y8BQBTomT0ykjE8599Q2cio55/scWVE54KjgRIpzSr3y5opNzhEPvxbZz1XJmoDjgKQac0qIczqgjdVvUSW3TCo65k/YVMF98KjiRIpxJinJKAAd49rXzd/m+XOGp4FRwRiaNKZqyjW5QrhRwKjpxIzEbfIoCp7Rh1aREOSWBU9GJiw5FWyZ8Bv/4xz9ErJfPTX5d1OG44S92GxR55Jiq4NAxukRJJZSlzlRTf7QqOAX9XCp15NzSSQGnRkf+0BDSUcFB5NRFxOKzz9gRCkf7uUFDx2MCB9tLiFxcj5E6T03dAarg/PepFRwgpGiDOnlOaRM4FR33TtlnyKKDU6Mc3u9q5QQNHUsbOBWdig4hWsGRnsuVIkLh2Ad19FzSSQWnzum4Q1rBqeBo78NxwcwGnL5GORUdN3SSgFOHVbzDKkRJLiDELmsLTkXHrXPSMKRPaQVHinBwdYtjyJOijdiIuLRfwZn1M619wiHGexn8/e9/F22vWDcGhrbrc/k7ZZ0U8PjswwUTm7Iu4Ni0Zyrjevm6pPIxOneObRYNTu5DNR8MUtUxdWqf/FTg4NhKQsT1WHMEgvuYrMBBBBQajcSqnzJi8dlXKkB89uODi66ODzjnnHOO+OAHPygGg8HwtcQSS4gdd9xR/PjHP56an0IebUd66aWXDre5duSSynN38NzaKx6cGuX4T0jr8PDJcwHn/vvvFyuvvPIIJDIqWP785z8vHnvssbEyyMPxlQSIz7HmhgTn8ViDU6Ocf3p/TcMn+khVxwcYtY4tOABj7rnnHoNEBQfriHbkfEQ78n59OnJpdTg7ei5tVXCUq1Q+w6a2Oqnw8NmP3Il9l23BWXvttUcQkaMZ7BvDLBNIGH6px1caID7HmwsUXMfRC3ByH1YBJB8MUtVRO7Lrug04mJuRIxbCRt3XzTffPFbOVBZ1fTpxiXW4OnzX7TiBk/OwKnd0UuHhux+147us24DTNkSS9ydPJhNS8mSyXBbLJQLie8xdgxG6f2dw2u7Z8dke6wqWT7ttw6MutvsikqIeOrwNOOpQad999x0bIhEkmDQmaCilbdypb8fvS71QQFzrZwFObpFTF6g07TMFHCH7aAMHV6YIDkqbIhYVHFzV4oZGbq8veIS8D1c4fMtXcDQ/sdrU+bvaFgJC7Lpt4Ojmb+QOry6rk8sYjqllONdDOmof6/piYlMvG3BqlNN+2T02HL7tc4Kju//mtNNOiwoO8OojHKHvyQYQ1zIVHE2Ek+sEtC8Isev5gINhli5KUYdTGII1Db90bfjmhXbQPtd3hcVUfvC3v/2t9cubPhPBvnV8Jnpj1elq+NS039h4+LTfBo7uUrcuakE5dXIZ4PgC4luvz3BwvDcTJjb5FRxDhFOjHPuvTLSBg46vfi8KsOBGP2zDMAqRjQ4bzOf4whFSj6NjTkIbNsjIZSo4DeBUdOzQsQFHN1SiK1ZNadPl8xBQbOpOAhic71GGxbQ8BKcOq8wPA2wa3nS5zWfoE6uOCg72o+vQ6s1/KjTARc2jb4jr2kuRx9khJ60tHTpT4AAdzpfvHA5nvVhzO67tdgmTbt/c8OjAMe0Dwyj52+IYagGa++67T1xzzTVj4NA3xFPgwrmPScPF9v1WcFqGVK64mMrrOn6XeSYQfPJdwGlqX41wYt/wxwmMri3bTjhJ5aKBk8swzQRA6vwucTHtu6nzu2xrAoeiFkz+4nXEEUcMIxm1/UcffXRsYvnUU0/VDs10nTvnvEkCpe299h4cDNFS42Lan6njd5mvdnyf9SZwbrrpprFhEiIXDKFoX0BJHmbRPA6VyRkT22Nr64iTsj0qODXKGZ+M7hIX3b6p04ekTeCgXfWSOIHSlCISomOy7dQllJsUWEzvcyLAqVFO89cmqGP7pm3gIMrR3WNjAgdzOeqxlICJ7TGaOuMk5EcHp0Y5+Uc5iHzUDu6y3gYO2sIcDeZkNt1007GIBxhhfoeuVpn2bduhSyk3CcCo73FiwKlRTnOUE4KODTgmRFzzS8HE9jjVDtn39cFf//pX4fLivFfHpy3O+3R82jJNCKfM183FdJmXEhxXoOTytgiUWK4UqCo4Fk8elWFKCUvTvroERt13KeAAnxIxcTnm3OGp4DiCU4dm40OzksCZBHQIqBzxcQYHwy+foRBnHTni6GK5KfJIuU2NNLpaLw2cSUIH+OQETwXHI8KpUc5olFMiOJOGTi7weIFTo5x87l5GRNVVZEP7VcFBPjp0KS8agkxS2lXU4w1O1+h0MZRS95ly+NS0L+r4XaWlgzOJ0Y6Ma0p8igUHc0IqAF2sN0GQcltX2GC/OnCQX0qEQ8cpd8JJXY6Nz+Avf/mLoJfL/TicZTknlF3b6gIp2mdKkEz74oDKBI5v2wRAKemk4uTzvkfAATyckLi05QoFV3nq/F2lJghS5vvCQPW4wUG7pWAjH6dPB5y0OhMPDuDqChvab0pcTPsiPHzSGOBUdP7Vy5sUx8CZxCina3RMCKTO98EGdWKBUyo6iHomLXKxfb8VnP/+ljNFG12lqXEx7c8HnZjgVHT6FelowalRzt87GWaZEEiZnyM4FZ3+oFPBkZ5W0VV0Q/tNCUvTvlzRiR3h0PHIE7SlLdsOOfpezggOXSrnSF2uVnGV5bqKZdsOodFF2oRHim2pwCF4fNLSgDIdb+kgVXCkCMcWF1O5LrChfaaAxbSPEsAhpEwdubT8UuFJAk5Xc0ImGGLmEwBdpCYQYueXBA7gKQ2XtuMtCZ9k4HSBTkxYmtruAhvaZ2xcdO2XBk7foh0CqQR4eg0O5oOaYIi1jTp/F6kOhNh5KjjYH3Xq3FPqrH1Lc8UnKTg1yklzuT02MGr7OnAqOnn8PEdu8PQenK6iHERPXUQ4tE8VhZjrJnAqOnmgQ9FbDvgkB6eLKKeiM/5sLE6AmsApCZ0+TigTNnLaJTyDZ599VoS+gEiqF9d9Oi7txJrrMbVLUUqXqQtIbeC4tCWXzX3+Rz0+uVPX5VnRnQwcCzgAq8/gdBEhdYkN7Vvu/E3LscDBPtVOXcJ6xWYWNupnURw4kzQko47fZdoEDW2LCQ7towRo5GNUO1pdfx4hNnBqlPM39kvwXUJD+6YO35RWcEafYlHhSRDhpASnqyinDq30k88pwAF4ckcuablGN7MAYo1wUqLjMunLWdY00Rszn6KNLtOuIxx5/yVhIx9rhec5wQ5ORYd/aAXMusSG9i13enk5VYQj71PuyCUuTyo+g2eeeUbYvABJyleqq14ph2cxo6CmtgmMWKkKjrofGYqclkuECsdcMlbW4AClvoJT0Qn7ykUbOARQTtjQsZSKTqnwOIFT0fkry2N0mqKRmNuo43OntuBgv9TRc0pLRqc0eLIGJ+V80CREOcCMGxu05wJOrugAwNLhKQEfZ3D6HOVwXs1qaytmJNPUdg7gVHTM9+1woZfrPE/24PQ1ygFITTDE3MaNjmuEQ/vPaVilHgtXx8+hnZzw8QKnz1FOyqFVX9DxBSfnSKcvQywVvK7xGTz99NNC9wIqsV+prnoBkRSvtmEU5/aYEZCpbYpM1DQEHLWttnU1Esl9Xe3wk75uBAcIxQYnVaSUAhvaBycqbW2ZYIidr6KQEhzsO3dkdMc36dDQ+58IcFLOA7Uhwb09Ni6m9mV0UoND+9Z17JzzqNNNctoITp+inIoO/1cuqON3BU6NduJf7eLGsRWcio7f/A93JNPWnikSiZ2PTt8lOIRezpFN27Fxd+qc26vgRJxQbkOCe3tsXEzt5wBOqdGOjFHOUHAdWzbgpJpATjm0wkQyNypt7ZlQiJmfCzg12sl/iGUFju6yuUteiqtdKcCiK1Ep0jZYOLeHYqSC49oeQZFbKkcfpS1zRSTc7SQBJ9U8UEXH/8ulrkjI5UPBQVu5YUPHUxo0uuPlRiOkvQqOx+/8pIhwaB+ckUxbWzIiLssc4OSMDvDRdeQS80Kw4Kg7+POf/6y909hlyGRbtg6t8r/i5QINleUCh9qj6CLHtERkTMfMAYhrG0NwKjruv2ZIEUiqtC064dxOHd825QYH+80RGzomUwcuPd8VD5/yvQUn9nxOKmjk/XCi0taWLTYoFwOc3NEBPqUD03T8PpjY1JkCp0Y5+Uc5wKcNCs7ttujEAqeio38sTxMUsbbZYGJTZgQcoMPxsp3T8SmXYh4oxbfY5cgl9jInQrq2YoJji55ajoY/OaexcMi53eLAAVIVHffJZx0UXHkqONSuikAX6zmDIx9bzkhwHlsUcFIMzyo6+aBjAgfwdIGMuk+5Y+e+zNm5c2wrGjgVHfs5odhDKrl9ij440yZwckEHCOWOjXx8OWLBcUxFg5NieJViPqf073e1gUO4qZFHF+typy5lmaOj59JGVHBqlGMf5ZSMji04NdoJe+BgLmiEHMfgqaeeEiEvjqtaujZ8rmC51unDPJA8XEqxTNGKnLqAI9fzWe4iKtLts5ToKOQ4Q2Ax1Q0GB1jpwODIcwXEtXwKcLCP2MOyFNDI+1ChSAkO9q0DoKu8kA5dYl0TJLb5WYMDtFwRcS1f0XG/2kX4EDypwckNHWBXIh5cx2yLDcqxgFNylAOgfNGZOXOmmGe+BcRgMJjolwrOpH8efXn/l112mTekJoTYwJk0dG699VYx38KLiSU/eqyYfvaTE/1SwZn0z6Pk97/UAd8VL3rJS8UFF1zgjU1T5FQEOCmGVi6Rzj333COmLbW0WGKbIyYaGupYFZx+/Ifz2kOuFi+bYy7x/888Kwo2gGjw5JNPCttXyNWsprocE8xtbbjO7ZjKP/TQQ2LZFVYS0zY7qGLz38iuglM+OEsfMUPMPs8C4qTTvhwNG2dwAFMTHCHb2sDg2G5CxDb/kUceEdPf9Bax6Pv3rthIw8gKTtngLHP0jWLuBRcXRx9/UlRssgIHWHGg0taGLS5qOWD75v9ZXSz03t0qNhI2GFZVcMoF5/Un3inmnraMOOzIL0THxgucmFFOzuis+s51xLT1dqjYKNhUcMrFZrnTHhBzLTldHPjZQ5Ng4w1OTHTaIhSu7WoE07S+zgYbiYXftU3FRoNNBadMcFY4/WHx6mXfIj69z37JsAkCp3R0moCRt71v0w+KRdf4YMXGgE0FpzxwVvz6n8T8K60hPrH7HkmxyRacXIZWW2y9rVjo7RtWbBqwKRmcabt8RcyxwlriBa+Ya+rGzRfPt7iY553bi6UO+n5v/+6vefM6YtuP7TTyFRFgkOI1eOKJJ0TbC9FMrFfIlS1dXa4h13Yf3UEs9tZ1envSAQquV2mTxq87/Cfi5Yu/YQoZ053Br9nsYLbPiOuzDm1ngbdvJD609XYj2KT8HpoVOACpFHA4oqOddv2kWPgNqwuEnqF/4EmoXxI4yx57y0hEY8KG8hff85u9OQfmW/VDYuNNN+8MG8DWOTix5oJ8I53d99xbLLDcWwQm1SYBC473WBI4GEIRJlhWQUH0M9dbN5kqg2WOz6jrNuZfaxvx7g026RQbJ3BiRjm5oLPfgZ8V8752usDlwq5PkJD9L7jlYWK5U36R7D2UAg4wIWzaIKFyQCnkb5FD3QXfs4NYZc33dI6NMziloeMS5Rx82BHi1YstLXAjVA4nie8xzL/JPsNO9YKXzSEW2vboJO+lFHBsPtPlvvigwGQygTPfhnsk+Qxtjs2nDG5UXeltqw9/kynlXI1pX9ZDKppYjjWX02WUc9xxx4m5XrOYwC3ePn/UnOpQR6F09uVWE/hSXsxjLA0cgIIrUYhe8GqaQC554hhfwXn9ym8Vf/zjH7OIboYRzuOPPy5ML0KGK80Rq1NPPVXMMc/8Al9ei9kpU7W9+B7niZcuvOzU/9AEz3wb7C6mn/1ElPdYCjgYUuGyN30mNmmpl8fx5eLXLv8G8dvf/jboaa2mSMU3f2DCBvlc0Mjt5ITOGWecIV4+x1zRI4BU2Mj7mX/jvcY61ksWWFIsttvX2dEpARybq1OIdjC3I6OEIZb8uZawjJ9NWXjJZcR9990XhA39oqMujQJOn9E599xzxYtf8lKBHxwq4STyOUb8jz7H9HeNwTP32z8glj3hDrb3XQI48pUnDKEwrDJFLwQOUp/Pvcs6C3/42OEPw91+++3RsNEBZPuzr40RDkU/coTCsRwzyrGZC7rwwguHnXCJvS8s7oTyOZkX+ciJ4oVzzDMCz2wveqlYcEueHxBTwcG8h81wJaSM6+dAdxMDkaaoBZfJ6bjarmS5HkPs8ovscKqYe94FxA033JAcGxNClE8RUSfgAK2u0Pne9743jGwW+9Q5E4ENneTLf/GXYp41t53qTNSpXrH028RSB10e9FkQOL/57kBstPpAzL3q5mP7of1xpfS+bFPaL6IbUx1EhAQTypc0YYyIDdMD1157bXbYEDpIrcDpy9Dq6qvxE4pziqU/eYbxpDOdjH3JR1T3ssVWHANh3nV3Fiue+ZjX50LgHLzDrB+Tf8lrXjvssE3RhM9nSnC41qVhEkGCOR1qA0MrXP6WsUE59aZAKp9biv888TvEV155ZdbYDMH505/+JOQXDaO4Uo4hmK4N1whpxowZw3BzqZ1OmTrRcjtxUh7PAh84YAydF796UTFt59OdPx8CZ9EFZoFDMCB91epbBUdR9NlQu7Rum/oM80xzPLb7TFEO/4HgM7nkkkuyx0YLDvDhwoba0YERmucCzo033jicSFviI8c4d6YUJ01X+1j6yJlizjeuNwbPXKtsJJY55mbrz4rA+cWFA7HXNgPxwtlfNdYmOsUrXvcWschHT7JuV/e5+IKDSKvpfhu0i+2IdGgfuYNDT1g4//zzBT0rjFJ5GJPT8kCObmiZoOBMQ4HR1bdB58477xw+YWHxrQ8POtF1J39f8hbd8TTxormV52vNNpv1HAaBQyk+F8ACYKjzyilAmm/93cQyX7je+W9C7fh+9oh0ZHgwjMLkMOZA0CaQoX0svN1xzsfne1yu9egJC18642tj2BA6lGYPTowoB3jp0AjNa0LngQceEMssP10s+qEDsz1xXE+0WOWHvwD37o9NdTbqdC9f8k1iyf0uafz8CBpK5WPEhDSGVNSenL5onoUb25XboWWqT+uTmNITFk489Uut2BA6ctolQNoIpw+RzsMPPzx8wsIi79vL+aSexJOY3jNwATLUsSl99bs/ZvwGPUFDKbUlpxjSzP/+fUfaxfe+5DI2y3Q8NmX7WAZfv8HXcI469gQvbGR4aDklQL0AB1GSHOkAzDe9fbX6hIWAH9kaTrLONtsIEBh2YfildmSChlJ1O60ve/xtU+3N9uKXidd73Hw4yeDQExYOPeJINmwIHTmNCdAAX+yiiIYz5Zz/kduyGYK9Y6216xMWArAhIDBxjAlk6uSUzvnGdQUmnKkcQUMp5avp6w67dqqtl01bYaq+Wq5pnY6hqUwft9ETFg74zCFRsZHhibE8BKckdNrAWXv9DesTFhiwkTstJlRxyZw6O6W4tI5yBA2lcl15ecn9L5tqY/Zl31HBsfw70RMW9th736KxAWBT4PQBnU0+sGl9woLlSSxDYLOMmwJxcyBhQyluIrzi5MEIOqb2cOs91XvVqpt7gWNqu6/5+Jnb+aavLnbebffisUkCDoZp8pCIa1mNdDbbcutsn7BAP4pFna2m+hsE+/i5+EyMy3gu8Ka1xTYf/fjwB7RiDHFStzkS4ZQU5QAuQufDH/mYmPaWfJ+wUMGZHGBUNEPAmf9tG4oPbvXhITbPPvvsSJoaCq79jYFTGjo77rJr9k9YqOBUcOSoxWYZT1jY6AObjSCjokPrXBikaGfwhz/8YfgThICG48V5pYvaMg3Ddttjz/qEhUhzNjadgsrgR73w415j/7tvPHoP1Jwrz/oaxWK7n1PncAx/Ozxh4V3rb2yFDaFTQgrQ2MFJFSHts/9BvXjCAnXa8tMnxHzv3X0MHfzcKX72FO+vgtP+8EF6wkIJgPgc4xCcEqIcefL5M4ce1osnLJSPzHgHwnd8Zl9u9TF4XrXaFiO/tYx7cvr4/kPeEz1hAU8b8enMJdSZAqcUdI455pjePGEh5OTMvS4eUYNH1YwMs/7frDuXcddx7u8h5fHhCQvLvvEt4rHHHustNgBxBJzc0Tn55JN79YSFlCd0F/vCw/gQ2YygMxiIF861gFhyv4srOP+dw8ETFpZabiXx61//utfYFAXO6aefLl42+5y9fMJCFxik3Kfx0TXvjffompTvL2Rf9ISFe+65RzzzzDNTrxKGRz7HOBbhIMoJeXFc6aI26CrVWWedNfwd4letOv6/pfq/J/f6HCu+s/5PbLia4trRUj66xvXYuihPT1i49dZbp6CR0el62QeUtjrs4HAPyy644IJhSK4+YYF+mQ0/nsT9u7k4+Zb/8q8Evu+z4FY8Tzbo4oTOcZ/mR9dsyvromhzfu3xM9ISFmTNnZolNE3ZtqDRtzxoc/E4rnh2le8KC/KPYMZ7/PO86Hxf1+z7jV6HkThOybHx0zQQAT09YuOaaa4rDJhSiKOBwRDlXXHGF8QkL+F9SHjpx/7o+bkrDt6MR5YR0qlq3GayYj67J9bOnJyxcfvnlvcKmCSLahshngMtwIXM2TXVpLsY1xbN18EAv0xMWaDgFdPCbtJwnFy7XAhv8lAJnu7UtMz4xHl2T4+dNT1i46KKLJg4bQmcITk7oXHfddWLehaaJpicsyMOped65PRsMiGhwN2zIF+5yPNFLOSbjo2v++wPnpbwP3XHSExbOO++8icUG6EyBA3R8X01Rjss2zNYvuuTrRNMTFmIOpwANwNGdMDXPHKFwfjbPP7pm3ZEhMyJZ10fXcB5TaFv0hIXTTv+qePrpp5O+KLLIJWUBhyNCuvfee8XSy63Y+oQFl+EUcKLHf7SdNBhC4Wcv67xNGlh0fw/5P5NXvuE9QY+u0bXfRR49YeH4k09LCo0Jtq7hYQMnBJ2HHnpIrLjyKsLmCQvycKrp6pT8pEUMu5ounQOZF7x8TlG/wdwdNsAA/znQxQAshzy6pgtc1H3SExY+f/RxWWCjQyg1QKzg+KDzyCOPiJXftqpYcINdW4cy8v+AODGxrv6RkSc/6IxO4Ka5HgyjcBlcbauupwVIjl7lZ3/7PLqm678dnrAw16JLi0MO/3y22OgAQl5MhAaPPvqo99yNac7HZd7mf9Z8t/UTFuQTEpGOelLJUQ1Bg6tYTU9QxI19uMGvDqXS4qL+7bBO/1GYrjy6PLpG136qPHrCwn4HfrY4bGIjNAQH6IS8TPC05b9r3Q2cnrBgGk7h8azyNsIGdyHL/1OqJxzmbXAJvH5zuXts8Lehv9scK6w19p8J/e3Mj65Zb+TRNVQ+dYph4DzLrCJ233NvgZ+Z4HqZICgtnwUcnyhpo/e9Xyyy+qbGE0s9UXTDKczLyFEPnbD4H7LtZkBENJgkrvM2eWAjP9MbkYz691fXp+18euOja9TyKdbpCQs77fpJNmh0YJWGjHy8nYDzoS22cn7CggwLQm9TVINyTRPEdOLVeZs8oKG/B4a99B8G/rb4GwIeilzxnwjm4eSItenRNep372g/MVM8YWGr7XeIio0KkNyZS1hmA8c2ytlmu494PWGBTjyclPIynaSEkM0JhXmbegk8L3CACf0tgQrN51AepYBHvViw1EGXi1cs/bap+lR2njW3Ffj6hM05EVoGT1jYdMttk2Kj4oP13NFhBacNndz1lwsAACAASURBVI/ttItYaKXVBEJPlz+wOpyiEwopTkCbEJz2h5+2xLxN/YnLvMCh/0Tw9zRhQ393lNFFsQtueYSY7UUvHYHnhXPMI/BFUfr7x0jxhIUN3/+hzrEpASB2cEzofGL3PcT8r19leG+F6x99eHViMP6oEUwuyiF2W7t13iYvZOjvBTwIE0oR8VAkg+0YcgEa2m668rjsCXeIud/+galyVH6O6e+aao/2y5HiCQvvXG+jLLHJEaAB7oMJfQGZptee++wf/IQFGR2ceG2TwrqTCffa1Ptt8kNHnjAGEKa7w/E3nwKk4UoW/va2j67RnSe2eXjCwpvXWEc89dRTbC8dEn3KYwEHYJnAOeCzh7A9YQEnHP7n04XTbSdJnbfJDxr6m8n/mbQNjynKabp0Tu1OP/sJMd8GzY+umVXW7fPBExamv3W14WOsOcGR2+oTNPReooJz1FFHZfGEhTpv49aZfDuhbz3cL4XIxTQ3I7cLaFDWDpzn3/fzj65ZbSo6oihJbtdlGU9YWOYNq4jf/e53bJGNDI1pmTptySkbOGqUc8IJJ2TxhAXM29SfCs0bHJowRvTa1vHdIpzR9y0/usb3J0joCQsPPvhgUmxUhEpFhxUcQudLX/pSNk9YqPM2o52urUOn3o5Jf4o4TBPBdExyWURFlO+S4tE1C255mFdd/GzKQkssLe66665OsSkZH3ZwzjzzzOHvEOMHh1xOhBhl8UPV9adC8wZHngjG5HHTeSDP9bTh1NSOzzZ6wsKNN96YFTYqPljPOfoZ/P73vxehL7rK9Y1vfGPqfyv6X6um45fz62dS3mcy97zzixkzZognn3yS9aUDo895LOAALEInNDVd7fLJb/vyqM92l2/Ct5V1/a1nm/L0LC/O9PHHHx9ejYmRrrXW85PAQBjL2McTTzwx8nrggQfESiutNPWf2fbbbz+yXS3vus6NiG97fYaG3hsbODmi4wOKTZ02SFy22yDiWoYTG7mtGODMNdesm/mAziabbCLwI/oEz/nnnz+CDcoDIFdU2sr7IhGrHnXQvqWs4FR0/J9a6opKW3kZCs5lTnQACw0vP/WpT00tU56aAhvUacMjdHssRELa7Qs87OBUdPJBByhxYiO3xQEPnhdPqNx///1iu+22m1qnfEoXX3zxJNjIWIUAEbNuyfgMcPNSyAvAcLxC537k+j7zPaY6NkMs2zIuQy3bsm2Rju92GRfuZcKKohrMz1AeEJLna7B87LHHCoBEZVxSGZCclmOClFvbMpDB4AArDnA4IyPgYwLEJ98WFNtytpjYlvNFpa0eNzRqey5whJbNCRv1WHIDIubxsIBT0XF/ppctJrbl2vDw3a4iwb0eColrfbWz57Yes7Pn0DYbOBWd7tEBTr6wtNXjhkZtzxWO0PK5QaM7nhyA4D6GwcMPPxw0h6PO/9ThlRs8thGMS7k2PHy3q0jEWA+FxLW+rqPnmsfd+btobwgO0PF5qdiErHNBNQlzQS74uJT1hci2XgygTG26wsNdPle0XI4rBkhB4OQaHeWMDiatbSeX28q5YOJS1hYQ33ImJGLkc0Pi2p5LBy+lrAwRjlleb1sOBqei0/xrh01XxdpAsd3ugolLWV9QbOvFAKapTVcsYpUvBRau45QRYgFnUtDhvtxeo50/Die5m5CIsS0WJD7tcnXqUtphA6ei099IB1GRbdTiWy4GLG1t+gARs04paIQc5+C3v/2t8H0BGY5XyGSzrm7oBLR81zLXctPQymeb7XDLppzLMMunrC9CPvXakEmxPSZKHG2HgBFaNwgcQMUBDnd0BIRyQ8cHFZs6NqDYlvHBxKWODyC+dVLAYrMPDiBStBEKiW39bMCZBHRizAEBJVtQbMq5AOJb1hcRn3o2KOjKrLnmmiNfJP3MZz4T/EXYFHBw7sMWEZdyg9/85jfeQyoainFFOTmiE3KJnb7pfOCBB478QJlN5OJaxgYTlzK+mLjU8wFEV4c+Z6Cg2055OlhMeTHAkffFCUMXbbkgI5cdglPRaf/Gu89cDnUEFZwSIh3CyQUQn7KEQUhKn3MbOLQPueOblmODI++3CzBi7lMGRl2eAqeiw48OdQQdOLHQ4R5iAR4fSFzrEAY+KX3OtuDQPuROry6nBEfed0wIcmh7BByg4/OioVVImtuwLHTSGfWpIxxwwAEjQyqfaEmu4zrccilPkQ1n6oqPa3n6nA866KDGIRVBY5PqwNHVk7EoabkrfFjA4YiOOK94cc0FhaJDHQHgUFsyHKHLLpC4lOXEhtpyRcSlPH3OAIfq6XBwybMFR26zJHB0x5oCITZwckTnO9/5jthwww3FnHPOOYw2kGId+bh0DgjoZEWKdfW+HoLCJ6W2ZXDQTig0qH/xxReLbbfdVkyfPn3kPWCfa6yxhsAw7p577gn6ITLCoi3Fgw/lDrrYYouJD3/4w+L6668fXkGTt+H4Lr300ikYCIiQlD5nGRxqTwbBZVk9ZhqunXfeeWLjjTee+szxO8tYv+yyy0aiK12HLjWPE6LBr3/9a69hVNPQK2RoxRXpbL311lMnBZ2QcrrrrrtagUMAcYJDbfnCA2jk92JaBrBXX311EDqIjEzg3HvvvVrw6HiwfxUjbLvkkkuGbRIKoSntTweO3HYoOECU9qVLsd20j1KxcT3uNpyG4HCjEwpOKDpt2NDJQpEPresiHAIHKUFhm8rtmuq4ooPIhdq1SfEeXYZTprIqOm3YyMemfs4EDtqUQfBdpn21gSO3b4KB8tUIR32cDe1TTZvQobZdO3Gfyk+BA3R8X03Rjs02DqCojW9/+9tjHXL11VcXV1555fCu6J/97GfCBNL+++8/cue0jI3PMp2MBJkJHdt8PNNa7byIdu6+++7hMG3mzJnDYRbtl1IMv9pgM0FjytfB98lPflJcd911Q+AQWemGezgmGRwVMp91ep8u4Mj46JZVcLAPoHP00UeLX/ziF0MoMYySf/CdjkMdXhE0OaVdITb41a9+5Q2NDJQNLE1lCIzQ9L3vfe8IONOmTRN33HHHCCSYVFbL4WRRwQmdfKYTkMDxiZJUjH7wgx+Io446ajgXhQ6tQgJ8aL+UfvGLXxwrp9bDugkXXb4K30YbbTRWH3NImM+h46A0JjhcUZMOnHPPPXcsIgM+6nvEnE5OuNgeSwqEhuD0CR06qSk99dRTx7ABJIh0qAylOnBC0KF2ZXAoUlIhCVlX8aD9Umq6D0itR+s6YOQ8gEFtU0qRjVwOy8COylCK+tjmE83o6lC7iHDk7brIxTZPBQeRjKkuoh46BkptO3kJ5TghmgKnD+hcccUVY394GkoBDvWl/i9tAscXHTr5dOBwRDuE1M9//nNx9tlni9122007jHEFpy3a+cIXvjDyOeNzVKGhdQyt6HOglMDhQofaVcEhfExQNOWr4GC4aCqPq250DJTecMMNw/IlgBJyjK4YjYBTOjq6+RsM0VRoaB1zO3SCIG0CxwcdatsEji86mMuhYZWKJu1TTn3AaYp21PkbXIYnYHSpfCxYlsGh8oSDT0rtm8ChNk1g6PJVcJrmh3TgqJf+Qzp1yXVVkMbAATq+L3lOx3e5aZ6nbduFF144AghOxKY5IRWc/fbbb6Q8weSbUkdoAoeGWLYphog2yNC+kWL/FA01pYRMW6oDx1QHoMjHgmUdOASPawpMqP02cAgem1QHjqke3g8dA6UqODrUUuflABcrOF1HSLohFfJM6KgdVwWnKTqyQYhOPkROtqA0lbvqqqvGTmzsAxEGUMGwCsMr2i+ltuAAIxMccj6iK2obKT5Hebu83DakcgVGV56OJSY4uNztAg5dyUqNisv+ugCIHZyu0aGTj9JTTjlFC44OJx04IejQMdBQrQkTm23bbLPNSEfHFbg777xzLHqh/VLqAg5FQDIa6jIus1PblOKSvFoO6ypOKM8Z4QAgOgZEXlg3weCSr0Y4uBJlqq+b06KyLgDkUjYmRIOHHnrIewhlGnr5DqfUem1DKN129XI3OuXtt98+ho5aDietCRxfdKgjEDg+80AyROoQEHdLy9uBBS6b034p9QGnDR41OsRXRlRwcIlevWSMYwJYukjFN4/eJ4FD7VCn90lVcLAPwKK2hRsg1feoi4ZywSTkODggGoIDdHKFR4dKU55uHgcddcaMGUN0kOqwwQnVBA4Ny2yGUlSGOoIMDm2TobBdRqemNpGi02NOB/UR6Zjmd1RwsC63gyEZAWNKVUzUeRy0h6tkdBMiUDHd+CffiEg4hKT0XlRw5DZVKNrWdeBgPxi20XfEEKnp3iNtp32obdHQL6Tz51ZXxoiOTc6j5cEvf/nLITaEjm9qinZc89Uox2fddCcxnZiUqv9LAxwZM0LGN6X9oF2CJiT9+te/PgIFtd+WAhgZNRUcgEzbTeCo+bhSputs6rGonzG2y+CokPms0z6bwJHxsVkGwtSuS0qYEDZITeDIZWIvEwJdp0NwJhGdk08+WahDFBUc4OOLDerRicoFDrBqwxQIHHnkkVP7xjEgj0BB2gQOlVOB0a23oQNsdEO8mOAQWDaoNJVRwcFwSh060d+XUtyro4MjB3B0x9UFPlPg9BEdFRV0AHRYTBgDkxVXXHGkY+rAMaFDJxlXqht2maIhRDoYFsrRA/Ck4RXQkLfhGOknOWzBsYUH6AAwOdrBvBmGV9iGl/oZXXTRRWPzPQSFmqp1Q9dtoyAVHAyf8FUNwCNvw+eM77PpJsKpk+cKDh2fmsaEaAScPqIjD5HUZfXkxfyPWkZeD4l25LomSDjyCQqblCIdeUilq6eLbmzzgIv6Oct1VWBirTdFM7G3UYcmeHTDLiqTc8oB0Rg4paOz2mqrCbx22WUXceaZZ4qf/OQnWkRuu+22sY5AkY+MjLoswxG6zAGMqQ0dHGoeDSkBj7pNty5Dgf/Z8T896gIVRDLydlrGvUEyOKhH2+Q0FjRqu7FxMbWP6IiiTkRDOcPic2y2GA0efPBBQS9gE/rynXRW67lONlN5QCOf4Fjed999xa233jr1rfhvfetbY8MpDAOaJqhVeHzXQ5FCfRMytvn44qp8pQ7rOmCa8uQhFH3eZ5111lQ7uGqGdepkVAb3EsnQcCyrqKRYN8Giy5evZmEeSFcmRp4PHLHrjIADeELB4YqQABAh4pJee+21Y+DQyd6UIhpqAgfbfJHR1esSHops8Hlg3oegagJG3YZ6TZ+nbhvwwZ3QHMjo2kgBjW4fTVjIkQ3eP8cvMDbtr2lbbExs2h8Dpw/ofPWrXx37n1XXASgPk8tt2NB2HR6+eV2hg0lnoIOJZMJGTlVcTOs0B0SfY1OKzoavZuigiJGngyFFnq7D4+oVJpZNP+Ghq5MyzwYKrjJacPqAzi233CIOP/zw4XwOhktqZ6B5HszxECYuqS8yunqh8MhYcC6boJHzEbHgjmcApg6fsI58XKbHEEuuFwMZtc0UwDTtIyUa3PviAkZtxwhOH9DRDcVcUGkrq8PDNy8UHdTnxIbakpHgXlaBiLneBEOKbdwgdNmeiojL+uCBBx4Q6gvYhL5C5oLUCWTfdR04vnlt+Lhs90XJVC9XrFKgJSMYE6ymtlOAxbWPLqHCvrXgAKBQcKh+hcf84/QmQHzzOeCJFSlNEj7AiQuILtqJiZIRnIqO+YfIXKKZtrK+uDTVq/D8bmq+qCkySbWtCzRi7JMDokZwKjpp0AFKTYD4bCsBHUQ98pAo9nIqYJr2EwOCXNq0AakVnIpOuegAqgrPrGhHBq0JhZTbcsEi1XEM7r//fmF6ARvfF83hhKYhc0ByXd+JZ7me74Szrl7bUMt1u08UpKvDBZSpHZrLiZ3KuMRcTokTx75SwWLaTyM4gMgXnFwiIxkdLMuA+Czr8PDNc0XFprwOEZ88Exhc+bHBofZjYqO2zQFCV22YgODObwUnF3QQKal4+K77QCPX8QXGVM8GEpcyPsCY6nABo2uHUEiVqkDEXO8KDu79FgcOZ6RT0TFfYteBZELENV+HBXdeKnSwn5jQ6NrmRiCX9nwwGtx3332i6WWa37HJDxmOqXVD5oJ8IyFdPTnS8V02RTq++TpsfPNcMXIpz40UtZcSK3VfOmByz+sSrFZwgJENLqYyKhwh67mgA4h8saF6vrg01fNFRq3ngohPWYKCO1UxSL2eOzRtx5cCoujgAKIQZNS6IehwDsn6jg4Q8sHEpQ43OHJ7qbHR7a+tg5eynRMiK3BCo5yKzvOP4aHoRk2bohbfbWrU4rvuAohvWRkK7mUdBF3klYKLz3G6gGQNDs3zmIZOtvlqxOK7Hhrp5BbtACFfXJrq+UKjq+cLiks9bnDU9rrAxrRPn85dep0BnoFs8yJwfFNbkEzlfGFS6+UGFcfQLBZWBJkOn9A8F4Rcy6rIpF43AZNDftdgWYMDlHyxoXomTGzzVTxC1kPh0V3BCs1Th1o+64REjDQUGbW+KySu5VNDo9tfDsjYHEMqiJzAqeiM/k5QKDC6+j7I6OrEAIfaVOEIXXeFxLW8DoKu8mw6f05luCFyBqcP6Kg/N3r++ecH/f6PDg6XPPV49tlnn5HL7ur2Cy64YGS7DhzkERCx0lBodPVdMVEfZojPCo8AMrUjQ3P77beP/SwqHoYol4m9nBMuPsfiCpIXOKWjo3bgb3zjG0HghE5Aq8cDcAAWQaJutwWH6scCh9rVwWHKwyN66P1g2VTOBIaaf8QRR0y1R+3iR/HVcuo6IDnllFPG6s6YMSMpODJoPh2+hDoySoN7771XuLyATciL5nN8U9v5nqZydGJSCnB854NC54JQn46DUgKHoiTKp/Sb3/ym1ffKCByOlHAJTW3BMUGk5uNH8OlzoXSDDTZoBQcAyY/LQV08q0uFKXRdBiX35RR4OYMDnELAySE6ohOT0hBwAFUoOnQclKrgEDy+KQc41AY3OGhPRcR1HU/goM+OUvnBhzo0fvrTn47V+drXvsYOjrrv3NExHR8XRl7glI4OnZSUhoJD0ZEvPHQclHKDQ1ARGhypLzxqhCO34woNlccQij47SnXPGpM7vzoUwyNt5O0plk2du8R8W5C8weFAJzTaaRo2NW2jk5JSgIPyBEdI6oMOHQele++9t9WQiSBxSTmwkduQwbBZbgJHrk+Y2KSIZuizoxTDqqa66rPKPvGJTyQHR0WtRGhcjzkIHA50fOdy5HpNuOi20UlJKYGjovOjH/1I7LTTTmLVVVcdO6FXWGEFscUWWwiU0QElw3PCCSeI9ddff6oN/G+65ZZbimuuuWY4HKPjoBTgoD5BQvmU2s7hUH05vfnmmwUiKBw/tYdl5GEbMKF8SmVgTMsyFk3LtuBQG01oyNsADB0vpaaHHF5++eVjZTHEUgHoet21M5dQfoBnH/u8gE3oK2QuSAbHdZlOSEplcAio448/fuykpPJqirJUT8bnxhtv1GIl19fth8AhtOTyWHa5jC9j893vfnfsMrDc9qKLLipQRs7DMrVhwsYlH1fYqH262ka4hKR4vDO1SymevKprc5dddhkpizkgGa+Yy10jFrJ/GTS0I6/bLnuDQ0h1iY7vkIxOSEpVcLBO22zTSy+9dAodipR0kZFNewAHcHGAQ220YUPHpT6uF/kEjpy6ICOX1YEjb9cBYZunHjsiN11dtdxJJ52UDBwTZiEQ5F5XxigYHMDTNTqu8FDnovS8884bfm2DohQViuWXX1788Ic/HIJyww03iEMPPXQMpL322msEHF3kgg5w2WWXDTGh4Rodg5wSOBQtyduw7BLhEDjqe0KnO+yww4bDKEByxhlnGKMfGRp1WcbCZrkNHGpDB0Vb3lZbbTX2d7n22mtH0FEjIXwOarsmFFLl5w5IyPEN7r77bq8hFUU4lJaEjtqBCRwMzYAOcAEYmKPBMIOwIZCQAiG5HZRt2g5sMMQiRChFPbkdLHODA+TUfQAbFQ/dcAr11HK6dYKiLbUFR25HBcG0Ls8P0ftVh1UqSlg3tYf8VMi07Sekk+dUdwgO0PF9ETi+aShUqO86F0QnI6Xnnnuu8xdT3/GOd4x0YqzL4FDblMrzPHI5YEZlKG0DB0M+AqsppegG7VHbSIEobVNTTGbLZbGslpHXdfg05WHCm9pvmvyWwXFZxnuj9pECeqqPSXF5G5a///3vN4LThFHotjZkStjuilkwOBwRUmp01JMO4LQNy66//nqBSAhDJxUbtIc8ipB0c0C6KIngUecUsA8ZEvV4bcGhNuQrZGgL6zIa8vLnPve5sU4pbzctNyEjb7MFh+oQFrbpzjvvPHb8P/7xj4fonHjiiSPbCKNQODjql4BLyDESTIO77rrLO7qRoyLfCIfqpURH7cAEjorOcccdJzbffPNhRKDWUdcJHKADmNTthIsuVedX5PkgoKG25QqO2j4iHhMcmB9S92cqq+YTEk2pKzjUli04wEU9fgwfUV+9IxkAqe1y4MHRRkjnzrnuEJy+oKOeaHvuuad2uKWWk8EBOpdccokVMnI7scABUPJ+sJwrODJABIWa+oIjt6Mioa4jcpE/M6yrECGqpPuO1Pq0zgEHZxs5Q2J7bFPg5IIOIh7faEedyNWBc/HFF4+cjDgxZXCuu+46LTZo++Mf/7hA1AOQ1GGVDA62yyc8IaGLbpCnG1LJZXVt0XDJJk0xpJKxkZdlKLDMAQ61STCoKSIa9TNT56awrtZrW+fEg6Mt206eU7nBnXfeKYBN6EseXvks09AqJFURABIqXscee+zYySiX0W0HUurEtLovrMtl1BMeUOluULz66qvHjgdDKrms2hYiHBmktmW0J7eBiVUTVCpOqGcqS/kyMG3L8pDN5vI+4eKSqtGM/N5pGfDJbbZhE3s7B0AltDEEJxd0QiegDz744JGOhZMLczAzZ84cwnPOOeeMRS/ofDI4iIropEQKtGRIsKyLglRw1ltvvZF2sB9MPMuQYFkth31yg4ObEuX3hGVMDhMYlOoun6MsbW9L27DBdldwqE0ZB5tlHZz0GeBv0dRGbFxs2i8BD59jnAKnD+hceeWVYx2LTjJTCmBkcHRooQyQATZf/vKXx+7BQdsqOBimqfsEXhhuARpENsBQLYN1bnAQAakTxxjG4QZGQgSX7dWhHR0blbFNCQld6gsOtdUEhbxNvSJF7wWp7h4kua68bINDqjI+HTy3OiPg9AGdT3/609pOLJ9wtAwAKPohdK666irxyle+0roNaksFBzjtuOOOVu2o+2sDB1fB2oZR6nZEOSZQ6D0g1ZWxhUYtR0jIaSg4clsyDOqy7p4bep/Yppa3WU8Fi+1+csPE5njGwAE6pcOz2WabtXZ0HTaEjm4eh05WpAACkY6ch2WKguQhmCmKobqASp1jsQFHHpqpuJjW29DBZ3L66aePvS8VEp91goITHGqTUhUNdaIYnzny1HK+67YwdFXOBoDUZQZ33HGHoBdhE5qGTkBzXDE7++yzxbrrrjsSrQAK5B1zzDGtX+e46KKLBOBaZJFFpjogOiSGVxQVoS2CA6k6PCPAMHckHwuOA3M3gA04oZ7ajoyWvA3LGK7J4Lgs01AO8xjULt4XhleASgeOCTA1H5PZ1CZXSrcAECou6Ve+8pWx40GeTRu+CMWo1xVYMfY7Ag7gCcWGKzriQCd0Elq+YkZ4hKYyJBzLLtjYlFWjLcz9qLD4rPtERaY6NmBwlomBSGibMTBI0eYYOFzocMHjc4ldV0fGI2Q5FByqz4ENtdEGCeZ8ENEgqjrkkEOGd0Kb6uBeIzk6QR0fYEx1TIj45HOiYttWKBSx6qfAgmMfWnA4h1g5DK8IoBBo5LqEBkdKaHCkJkRwOV5GBMsAiK6YoR6GWsBILWf60qkJFNt8H2Ca6tiCwVkuFh6c7XIgwdnGAA8Da3oRPi4px7CMK0LiGprlNDzzwalt8lqFBuuY2zEhZpNvi49vuSaAYm3jBIuzLU6kYrbVCg4wcsFGLssBD0eElCM6iJhCIyQXeHAFTXeToQ4awkZ3o6INNGoZX1Bc6sUCpqldTjBitBUTDt+2rcDpGh2uaIeGVhypPMQKWU6JDoDCFS5EO7gcr2JD8zymr2GokLiuuwASUrYJiZjbYqARo01fLDjqWYPTF3RqtGP/5FRXUGzLh2DiUjcmLm1tx4AiRZscqDS14QRORWf8lxFDohtd3ZCIx2WIZVvWFhGfci54hJZtAyL29hRYxN5HEyS22wa33XabaHsBGo6XPL/juswxH8Q1NOOMkjgmo0OQMtW1BcmnnA9OTXVCMfKtHxsprvZjQ+TSvhU4BBIHOiFREpDqMzwVn/uCrorJKPkiElqPC4nU7bigEVLWCRzAw4VOCDy5oZNbxIOhmilyCcn3iWZs68hYcC6HAhJaPzUcMfYXAoxa1xmcXKIdLnRyHWblGu0ALFtEfMtxgiO3FYoHR/0YIOTQpgqLaX2AB8Hbvgib0JQrSnKdB5LL5wQWx2V6uQ3dZDRHXkh0pNb1xcilnoxNV8scSHG20TVOTuAAplBs5Pp9ggfDqpCXDAbXMgcyujZUPHzXXfAILdsVOPJ+OeHgbisVRM7gVHSe/70gU4QUgg73XBDg0oHBlecLja5eKCgu9WUEulzmRiNWe5wYeYFDQzA5WglZ5op0QiaiOa+Ahc4LcUU4cjtcyOja0QHim+cCB0fZLsHR7TsWGrHbtUVpcMstt4iQF+Hjk4YgJdcNAUue1wldNkU9tvmh0ZGuvowO57IOHt88X5x863FAZduGDpUS87jACgYHWPlgQ3VkOEKWQ9AJjYxUqGyBMZXTwRGax4mN3JYvMqZ6voj41rOFg6NcidC4HLMNSizg5IIOwAqBR4UjZN2EiW1+KDCm+jIWnMsmQHzzfQEJqceBiksbLp25L2XZwKFhGUUurmlIdKPWzQUdgGULjKmcCY6QfE5o1LZ8gWmqF4KIb10XODjL9gUW0/sY4JEZeBEYHKkrTbzK/AAAAIhJREFUNlRehSN0vcLTfKlexYJzvQkQ322+eITW4wTFtS1Txy01f3DTTTcJehE+vikHVmiDAPJNQ6AKQUpXN2RYxhEh6SKnkOhIrcuJVFNbvkjZ1AsFias+MEJbriiVUh5IjoDDAQ8XOqHw5IQOIKrwjP+0RxMwpm02gPiW4YIjRjuloNJ2nP8HCyXNqaZI6hsAAAAASUVORK5CYII=[/img][br][br]Garis tegak lurus sebuah bidang jika garis tersebut tegak lurus dua buah garis berpotongan yang terdapat pada bidang.
[b][color=#980000]Jarak titik ke bidang[br][/color][/b][br]Jarak antara titik A ke bidang V adalah panjang ruas garis yang menghubungkan tegak lurus titik A ke bidang [i][math]v[/math].[/i]
[b][color=#ff0000]Contoh[/color][/b][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik F ke bidang ABCD adalah . . .[br]Langkah penyelesaian[br]1. Gambarlah kubus ABCD.EFGH[br]2. Proyeksikan titik F tegak lurus terhadap bidang ABCD
[b][color=#00ff00]Pembahasan[/color][/b][br]Titik F diproyeksikan tegak lurus ke bidang ABCD, sehingga FB tegak lurus terhadap bidang ABCD.[br]Jarak titik F ke bidang ABCD = panjang rusuk FB = 6 cm[br]Jadi, jarak titik F ke bidang ABCD adalah 6 cm.
[b][color=#ff0000]Contoh[/color][/b][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Jarak titik A ke bidang BDHF adalah . . .[br]Langkah penyelesaian[br]1. Buatlah kubus ABCD.EFGH[br]2. Proyeksikan titik A tegak lurus terhadap bidang BDHF
[b][color=#00ff00]Pembahasan[/color][/b][br]Titik A diproyeksikan tegak lurus terhadap bidang BDHF, sehingga AP tegak lurus terhadap bidang BDHF.[br]Jarak titik A ke bidang BDHF = panjang ruas garis AP ([math]AP\bot BD[/math])[br][math]AP=\frac{1}{2}AC[/math], AC diagonal sisi[br][math]AP=\frac{1}{2}\times10\sqrt{2}[/math][br][math]AP=5\sqrt{2}[/math][br]Jadi jarak titik A ke bidang BDHF adalah [math]5\sqrt{2}[/math] cm.
[b][color=#ff0000]Contoh[/color][/b][br]Diketahui kubus ABCD.EFGH dengan panjang rusuk 9 cm. Jarak titik C ke bidang BDG adalah . . .
Lalu berapakah jarak titik E ke bidang BDG?[br]Dapatkah kalian mengambil kesimpulan?[br]
[color=#ff7700][b]Pada kubus ABCD.EFGH dengan panjang rusuk [/b][/color][math]a[/math][color=#ff7700][b] satuan. Berlaku bahwa[br][/b][/color][br]1. Jarak titik C ke bidang BDG adalah [math]\frac{1}{3}a\sqrt{3}[/math] satuan.[br][br]2. Jarak titik E ke bidang BDG adalah [math]\frac{2}{3}a\sqrt{3}[/math] satuan.
