Menentukan Gradien Persamaan Garis Lurus
Petunjuk Umum
[b]1. LKPD ini memuat 3 fitur yakni[/b][br]a. Ringkasan Materi[br]berisi rumus mencari gradien dan contohnya.[br]b. Aplet[br]berisi lembar aktivitas siswa yang berupa grafik interaktif yang dapat digunakan siswa untuk menunjang LKPD[br]c. Lembar pertanyaan dan jawaban[br]Berisi pertanyaan-pertanyaan yang wajib diisi siswa untuk memperdalam materi.[br][b]2. Bacalah dan pahami ringkasan materi tiap bagian[br]3. Bacalah dan jawablah pertanyaan-pertanyaan yang tersedia, kemudian ikuti perintah yang ada pada tiap pertanyaan menggunakan aplet yang tersedia.[/b]
BAGIAN PERTAMA
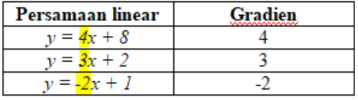
[b][size=150]A. Gradien garis yang memiliki persamaan y=mx+c[/size][br][/b][br]Jika diketahui bentuk umum persamaan garis [math]y=mx+c[/math], maka gradiennya adalah koefisien dari variabel x, yaitu [i]m.[/i][br][b][i][center][b][i]y = [/i][/b][b][i][color=#0000ff]m[/color][/i][/b][b][i]x + c[/i][/b][/center][/i][/b]
contoh :

Aplet 1
Pertanyaan Bagian Pertama
1) Masukkan persamaan [i][math]y=2x+5[/math] [/i]ke dalam kotak “persamaan =” yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
2) Masukkan persamaan [i][math]y=-x+6[/math] [/i]ke dalam kotak “persamaan =” yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
3) Masukkan persamaan [math]y=-3x+4[/math]ke dalam kotak “persamaan =” yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
4) Masukkan persamaan [i][math]y=x-8[/math] [/i]ke dalam kotak “persamaan =” yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
2) Masukkan persamaan [math]y=12x-6[/math]ke dalam kotak “persamaan =” yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
BAGIAN KEDUA
[b][size=150]B. Gradien garis yang memiliki persamaan [i]ax + by + c = 0[/i][/size][/b][br]Untuk mencari gradien jika diketahui persamaan garis [i][math]ax+by+c=0[/math][/i], maka kita dapat mengubah persamaan tersebut ke bentuk[math]y=mx+c[/math][br][center][math]ax+by+c=0[/math][br][b][/b][math]by=-ax+cy[/math][br][math]y=-\frac{a}{b}x+\frac{c}{b}[/math][/center][justify]sehingga gradiennya adalah koefisien dari variabel x, yaitu[math]-\frac{a}{b}[/math][br][/justify]

Aplet 2
Pertanyaan Bagian Kedua
1) Masukkan persamaan [i][math]4x-2y+6=0[/math] [/i]ke dalam kotak yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
2) Masukkan persamaan[math]-3x+3y+1=0[/math][i] [/i]ke dalam kotak yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
3) Masukkan persamaan [i][math]7x-14y+2=0[/math] [/i]ke dalam kotak yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
4) Masukkan persamaan [i][math]-6x+3y+1=0[/math][/i]ke dalam kotak yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
5) Masukkan persamaan [i][math]6x+8y-10=0[/math] [/i]ke dalam kotak yang tersedia[i].[/i] Kemudian, klik kolom “tampilkan grafik”. Cari gradien dan tulis pada lembar jawaban. Kemudian, periksa kebenaran jawabanmu dengan klik kolom “tampilkan gradien”.
BAGIAN KETIGA
[b]C. Gradien Garis yang Melalui 2 Titik ([i]x[/i][sub]1[/sub], [i]y[/i][sub]1[/sub]) dan ([i]x[/i][sub]2[/sub], [i]y[/i][sub]2[/sub])[br][/b][br]Jika diketahui sebuah garis yang melalui titik ([i]x[/i][sub]1[/sub], [i]y[/i][sub]1[/sub]) dan ([i]x[/i][sub]2[/sub], [i]y[/i][sub]2[/sub]), maka mempunyai gradien m dengan rumus sebagai berikut,[br][center][math]m=\frac{\left(y2-y1\right)}{\left(x2-x1\right)}[/math][br][/center]

Aplet 3
Pertanyaan bagian ketiga
1) Geserlah titik A hingga menjadi titik (3, -4). Kemudian geserlah titik B hingga menjadi titik (2, -1). Bagaimana gradiennya?[br]
2) Geserlah titik A hingga menjadi titik (3, 4). Kemudian geserlah titik B hingga menjadi titik (2, -5). Bagaimana gradiennya?
3) Geserlah titik A hingga menjadi titik (3, 1). Kemudian geserlah titik B hingga menjadi titik (2, 1). Bagaimana gradiennya?
4) Geserlah titik A hingga menjadi titik (0, -4). Kemudian geserlah titik B hingga menjadi titik (0, 1). Bagaimana gradiennya?
5) Geserlah titik A hingga menjadi titik (-5, -4). Kemudian geserlah titik B hingga menjadi titik (-3, -1). Bagaimana gradiennya?
BAGIAN KEEMPAT
[b][size=150]D. Gradien Garis yang Melalui Titik Pusat (0, 0) dan Titik ([i]x[/i], [i]y[/i])[br][/size][/b][br]Jika diketahui sebuah garis yang melalui titik pusat (0, 0) dan titik ([i]x[/i], [i]y[/i]), maka mempunyai gradien m dengan rumus sebagai berikut[br][center][math]m=\frac{\left(y2-y1\right)}{\left(x2-x1\right)}=\frac{\left(y2-0\right)}{\left(x2-0\right)}=\frac{y2}{x2}=\frac{y}{x}[/math][br][br][br][/center]Sehingga gradien garis yang melalui titik pusat dan titik (x,y) adalah [math]m=\frac{y}{x}[/math]

Aplet 4
Pertanyaan Bagian 4
1) Geserlah titik A hingga menjadi titik (0,0). Kemudian geserlah titik B hingga menjadi titik (2, 1). Bagaimana gradiennya?
2) Posisikan titik A tetap berada pada titik pusat. Geserlah titik B hingga menjadi titik (-2, 6). Bagaimana gradiennya?
3) Posisikan titik A tetap berada pada titik pusat. Geserlah titik B hingga menjadi titik (-3, 0). Bagaimana gradiennya?
4) Posisikan titik A tetap berada pada titik pusat. Geserlah titik B hingga menjadi titik (0, -3). Bagaimana gradiennya?
5) Posisikan titik A tetap berada pada titik pusat. Geserlah titik B hingga menjadi titik (-4, -5). Bagaimana gradiennya?