Isaac Barrow y el Teorema Fundamental del Cálculo
Isaac Barrow y el Teorema Fundamental del Cálculo
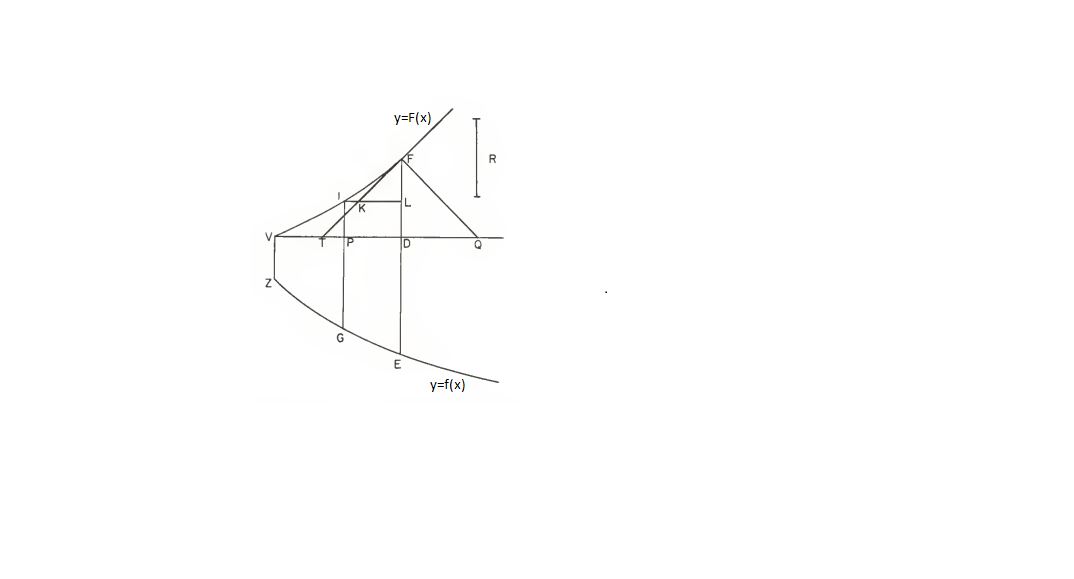
En esta actividad se contempla una ilustración de la versión geométrica del Teorema Fundamental del Cálculo desarrollada por Isaac Barrow en sus lecciones [i]Lectiones [/i][i]Geometricae [/i]de 1670 trabajo en el cual colaboró I. Newton. El resultado que trata sobre el TFC corresponde a la Proposición XI de la Lección X y establece lo siguiente:[br][br][b]Proposición:[/b] Sea ZGE una curva dada por y=f(x) cuyo eje es VD y consideremos las ordenadas (VZ, PG y DE) perpendiculares a este eje y que crecen continuamente desde la ordenada inicial VZ (Figura 1); sea VIF una curva dada por y=F(x) tal que si una línea recta EDF se traza perpendicular al eje VD, que corta a las curvas en los puntos E, F y a VD en D, el rectángulo determinado por DF y una longitud dada R es igual al área de la región VDEZ; sea T un punto sobre VD talque [center][math]\frac{DF}{TD}=DE[/math][/center]y únase T y F. Entonces TF toca a la curva VIF en el punto F. [img width=14,height=20]file:///C:/Users/SAULOM~1/AppData/Local/Temp/msohtmlclip1/01/clip_image034.png[/img]
Figura. 1: Ilustración de. Barrow para la demostración del TFC, (Struit, 1969).

La demostración de este resultado se puede revisar en, [i]Struit, J. D. (1969). Source Book in Mathematics 1200-1800. Cambridge, Mas: Harvard University Press[/i], y fundamentalmente consiste en demostrar que la recta TF está siempre por debajo de la curva VIF.[br][br]Si se interpreta, en notación actual, lo que muestra la Figura 1, se tiene que la curva ZGE se expresa por una función y = f(x), la curva VIF se representa por y = F(x). El segmento VD representa el eje de abscisas donde toma valores x. La cantidad F(x) representa el valor del área bajo la gráfica de f comprendida entre el punto V y x. Dado un punto de abscisa D, Barrow demuestra que la pendiente de la tangente a y= F(x) en el punto F, es decir en el punto (D, F(D)), es igual a f(D) = DE. [br][br]En la siguiente actividad se ilustra este resultado y se interpreta en terminología moderna. En la casilla de entrada se define la función y=f(x) considerada y esta se puede modificar a voluntad. Al ir activando los botones se va desarrollando cada paso de la ilustración.