Funções
Livro de Funções criado para a matéria de Tecnologias no Ensino de Matemática - 2025
Table of Contents
- Introdução às Funções
- O que são funções?
- Tipos de Funções
- Funções Polinomiais
- Função de 1º Grau ou Função Afim
- Função de 2º Grau ou Função Quadrática
- Funções Trigonométricas
- funções trigonométricas
- Função Exponencial
- Função Exponencial
- Referências Bibliográficas
- Referências Bibliográficas
O que são funções?
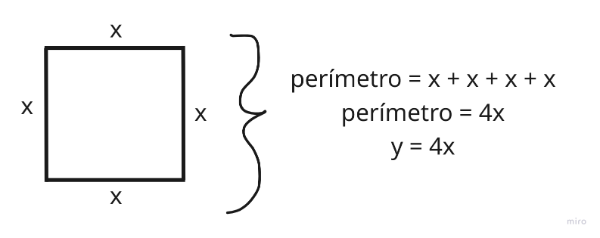
Não é raro, durante nossas vidas, nos depararmos com situações em que[br]podemos, de alguma forma, estabelecer um relacionamento entre grandezas.[br][br]Por exemplo, o gasto com o celular pré-pago, durante um mês, depende da quantidade de[br]minutos falados; o tempo gasto numa viagem entre duas cidades depende da[br]velocidade adotada no percurso.[br][br]Essas e muitas outras situações podem ser mais bem compreendidas se[br]fizermos uso de uma das melhores ferramentas matemáticas para a descrição da[br]realidade: a função.[br][br]Quando afirmamos, por exemplo, que o perímetro de um quadrado é igual ao[br]valor da medida de seu lado multiplicado por quatro, estamos descrevendo verbalmente[br]uma função cuja fórmula matemática correspondente pode ser dada por [b][size=150]y = 4x[/size][/b], em que[br]a variável independente [b]x[/b] corresponde à medida do lado e a variável dependente [b]y[/b][br]corresponde ao perímetro do quadrado.
No geral, uma função é uma entidade matemática que é utilizada para relacionar duas grandezas que variam, como nos exemplos acima, relacionamos o gasto com o celular pré-pago com a quantidade de[br]minutos falados; o tempo gasto numa viagem entre duas cidades e a velocidade adotada no percurso; o tamanho do lado de um quadrado com o seu perímetro.
Definição
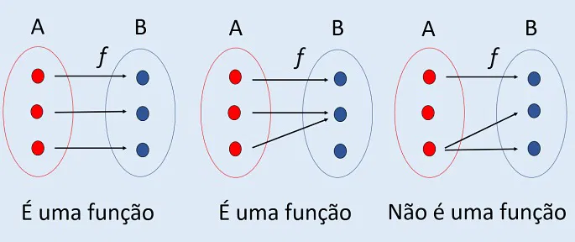
Uma função matemática é uma relação entre dois conjuntos quaisquer que[br]associa, a cada elemento de partida, denominado domínio, um único elemento de um conjunto[br]de chegada, denominado contra-domínio. Os elementos do conjunto contra-domínio que são[br]imagem de algum elemento do domínio constituem o conjunto imagem da função. [br][br]
Denotamos por
[math]f:A\longrightarrow B[/math][br][math]x\mapsto f\left(x\right)[/math][br][br]ou[br][br][math]f:A\longrightarrow B[/math], tal que [math]y=f\left(x\right)[/math]
Representação de uma Função
Há quatro maneiras distintas de se representar ou descrever uma função, a saber:[br][list][*]Descrição Verbal;[/*][*]Fórmula Matemática;[/*][*]Tabela de Valores;[/*][*]Gráfico.[br][br][/*][/list][size=100][size=150][u][i]Exemplo:[br][br][/i][/u][/size][/size][b]Descrição Verbal: [/b]O queijo que um agricultor produz está relacionado com a quantidade de leite que as suas vacas produzem, e após alguns estudos, ele descobriu que para produzir 1 quilo de queijo ele precisava de 5 litros de leite.[br][br][b]Fórmula Matemática: [/b]Vamos considerar que a quantidade de queijo é [b]y[/b] e a quantidade de leite é [b]x[/b].[br]Então a fórmula matemática é dada por:[size=150][b][i][math][/math][/i][/b][b][i]5y = x[/i][/b][/size]
[b]Tabela de Valores:[/b]
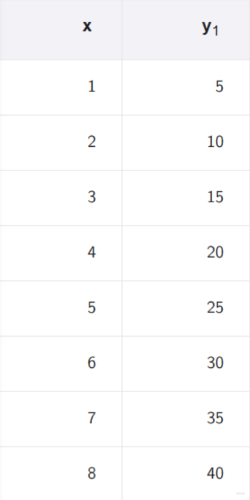
[b]Gráfico:[/b]
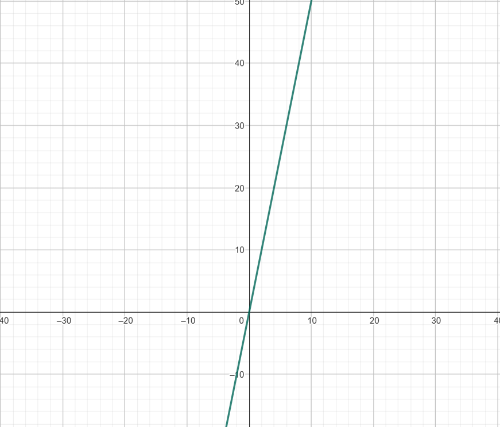
Responda
O que é uma função?
Quais das seguintes representações podem ser usadas por uma função?
Função de 1º Grau ou Função Afim
Definição
Uma [b]função de 1º grau [/b]ou[b] função afim[/b] é uma função [math]f:\mathbb{R}\longrightarrow\mathbb{R}[/math] dada por[br][math]f\left(x\right)=ax+b[/math] para todo [math]x[/math] real, em que [math]a[/math] e [math]b[/math] são números reais dados e [math]a=0[/math].[br]Caso tivéssemos [math]a=0[/math] e [math]b[/math] um número real qualquer, a função se tornaria[br][math]f\left(x\right)=b[/math]. Tal função é denominada de [b]função constante[/b].
Exemplo de Funções Afim
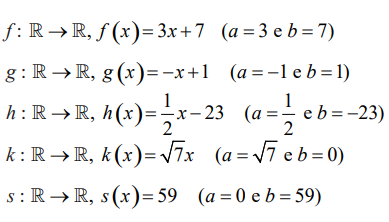
Responda as questões
1)
Qual é o valor de [math]f(3)[/math] para a função afim [math]f(x)=2x+1[/math]
2)
A função [math]f(x)=ax+b[/math] passa pelos pontos [math](1,3)[/math] e [math](3,7)[/math]. Quais são os valores de [b][math]a[/math][/b] e [math]b[/math]
3)
A função afim [math]f(x)=ax+b[/math] é tal que seu gráfico intersecta o eixo [math]y[/math] no ponto [math](0,−4)[/math] e é perpendicular à reta [math]g(x)=\frac{1}{2}x+1[/math]. Qual é a expressão de [math]f(x)[/math]?
funções trigonométricas
Definição
As funções trigonométricas, também chamadas de funções circulares, estão relacionadas com as demais voltas no ciclo trigonométrico.[br]As principais funções trigonométricas são:[br][list][*]Função Seno[/*][*]Função Cosseno[/*][*]Função Tangente[/*][/list]No círculo trigonométrico temos que cada número real está associado a um ponto da circunferência.[br]
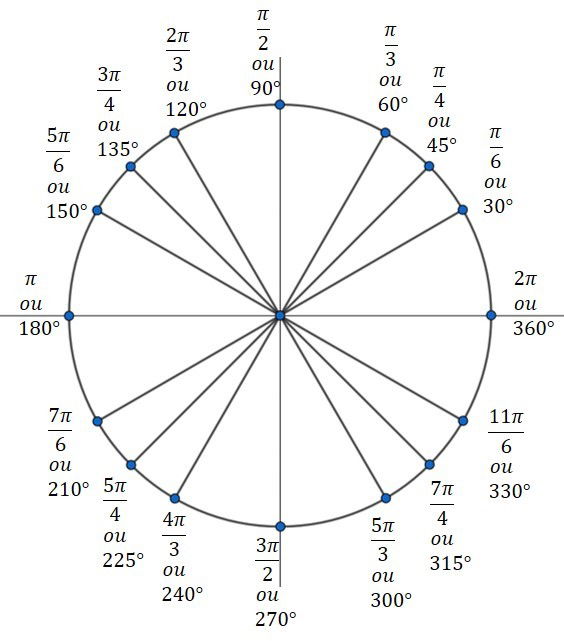
[img]https://static.todamateria.com.br/upload/ci/rc/circulotrigonometrico3-0.jpg[/img]
Dada a função f(x) = sen x + 3, o valor numérico da função para x = 3π/2 é:[br]
Analise o gráfico da função trigonométrica a seguir:[br][img width=459,height=452]https://s5.static.brasilescola.uol.com.br/exercicios/2021/08/questao-grafico-funcao-trigonometrica.jpg[/img][br]A lei de formação que descreve a função demonstrada no gráfico é:
Sobre as funções trigonométricas, julgue as afirmativas as seguir:[br]I → A função seno (f(x) = sen(x)) e a função cosseno (g(x) = cos(x)) possuem imagem no intervalo [–1,1].[br]II → A função tangente (tg(x)) possui imagem entre [2, – 2].[br]III → A função seno é uma função periódica.[br]Marque a alternativa correta:
Função Exponencial
Função Exponencial é aquela que a variável está no expoente e cuja base é sempre maior que zero e diferente de um.[br]Essas restrições são necessárias, pois 1 elevado a qualquer número resulta em 1. Assim, em vez de exponencial, estaríamos diante de uma função constante.[br]Além disso, a base não pode ser negativa, nem igual a zero, pois para alguns expoentes a função não estaria definida.
Exemplo
A base igual a - 3 e o expoente igual a 1/2. Como no conjunto dos números reais não existe raiz quadrada de número negativo, não existiria imagem da função para esse valor.[br]Exemplos:[br]f(x) = 4[sup]x[/sup][br]f(x) = (0,1)[sup]x[/sup][br]f(x) = (⅔)[sup]x[/sup] [br]Nos exemplos acima 4, 0,1 e ⅔ são as bases, enquanto x é o expoente.
Gráfico da função exponencial
O gráfico desta função passa pelo ponto (0,1), pois todo número elevado a zero é igual a 1. Além disso, a curva exponencial não toca no eixo x.[br]Na função exponencial a base é sempre maior que zero, portanto a função terá sempre imagem positiva. Assim sendo, não apresenta pontos nos quadrantes III e IV (imagem negativa).[br]Abaixo representamos o gráfico da função exponencial.[br][img width=630,height=556]https://static.todamateria.com.br/upload/ex/po/expoencialgrafico3.jpg[/img][br][br][br][br]
Exercícios
Dada uma função de R → R com a lei de formação f(x) = [i]a[/i][sup]x[/sup], em que [i]a [/i]é um número positivo diferente de 1, julgue as afirmativas a seguir:[br]I → Essa função será crescente se [i]a [/i]for positivo[i].[/i][br]II → Se x = 0, então, f(x) = 1.[br]III → Essa é uma função exponencial.[br]Marque a alternativa correta:
Dada a função f(x) = 2[sup]x+3[/sup] + 10, o valor de x para que f(x) = 42 é de:[br]A) 2[br]B) 3[br]C) 4[br]D) 5[br]E) 6
Um botânico, encantado com o pau-brasil, dedicou-se, durante anos de estudos, a conseguir criar uma função exponencial que medisse o crescimento dessa árvore no decorrer do tempo. Sua conclusão foi que, ao plantar-se essa árvore, seu crescimento, no decorrer dos anos, é dado por C(t) = 0,5 · 2[sup]t – 1[/sup]. Analisando essa função, quanto tempo essa árvore leva para atingir a altura de 16 metros?
Referências Bibliográficas
[b]BOURCHTEIN, Ludmila; BOURCHTEIN, Andrei. [/b][i]Introdução às funções elementares.[/i] São Paulo: Edgard Blücher, 2023. 455 p.[br][br][b]COSTA, Kiara Lima; LIMA, Diego Ponciano de Oliveira; VERAS, Darlan Portela. [/b][i]Matemática básica I.[/i] Fortaleza: Universidade Aberta do Brasil: Instituto Federal de Educação, Ciência e Tecnologia do Ceará, Diretoria de Educação a Distância, 2017.[br][br][b]CAETANO, Paulo Antonio Silvani; PATERLINI, Roberto Ribeiro. [/b][i]Funções elementares: módulo II.[/i] Cuiabá, MT: Central de Texto, 2013. (Matemática na prática. Curso de especialização em ensino de matemática para o ensino médio)[br][br][b]DANTE, Luiz Roberto. [/b][i]Matemática: contexto e aplicações – ensino médio.[/i] 2. ed. São Paulo: Ática, 2010. 3 v.