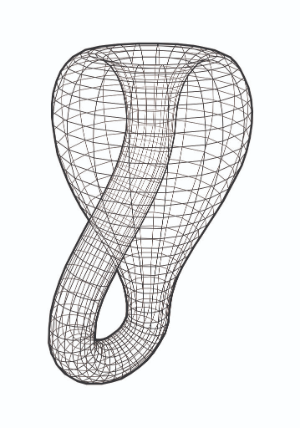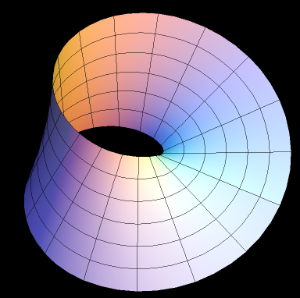
Parameterizing the Möbius Strip
What is a Möbius strip?
Easy visualization - Long strip of paper with a half twist, connected at the ends.[br][br]What makes it unique? - One-sided, embedded in a 3D space.[br][br]Applications? - Motor belts, recording tapes, electrical resistors.

Parameterization of a Möbius Strip - Visualized
How Does the Parameterization Work?
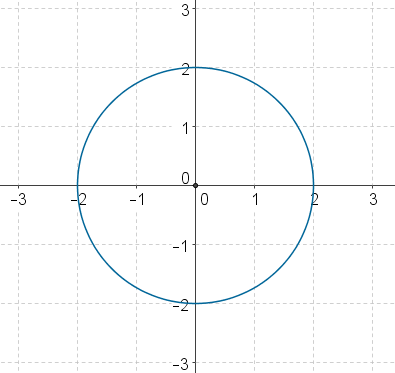
Take only the parts of the equations that don't contain t:[br][br](2cosθ, 2sinθ, 0)[br][br]This defines a circle in the XY plane with radius 2 centered at (0,0,0). Essentially, if we ignore the t-terms, we're describing a point moving around a circular, flat loop.
Circle of Radius 2 Centered at Origin
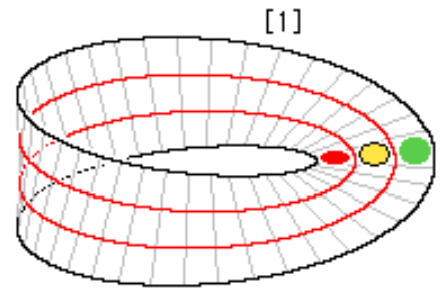
How Does the Rest of This Parameterization Change the Motion of This Point?
Let's start with the cos(θ/2) components in X and Y. These terms scale the outward displacement in the radial directions by cos(θ/2). For example:[br][br]When θ=0: [br]cos(0/2) = cos(0) = 1, the displacement is maximal and directed outwards.[br][br]When θ=2π: [br]cos(2π/2) = cos(π) = -1, the displacement is maximal but flipped.[br][br]Since we're connecting at the ends (0 and 2π), this implies that the orientation of the outward displacement is reversed, giving us our half-twist.[br][br]In the z direction, sin(θ/2) scales the vertical displacement. For example:[br][br]When θ=0 or 2π: [br]sin(0/2) = sin(2π/2) = 0, no vertical displacement[br][br]When θ=π:[br]sin(π/2) = 1, the displacement is maximal[br][br]How we can show mathematically that we're getting a half-twist?[br][br]At θ=0, take a point on the strip at t=B. Plugging this in, we get:[br](2+B, 0, 0)[br][br]At θ=2π, the same point t=B gives us:[br](2-B, 0, 0)[br][br]This shows a mirroring across the initially defined circle, meaning a point traveling along the strip returns to the starting point with an inverted orientation.
Half-Twist Visualized
But Wait, What About Cos(θ) and Sin(θ)?
These terms simply keep the outward displacement radially centered with our circle (think planet orbiting the sun). This is because (cosθ, sinθ) is our unit normal vector to a circle centered at the origin.
Final Notes
If you haven't realized already, traveling around the Möbius strip radially by 4π will bring us back to our starting point with our initial orientation. This is what makes them so useful; If you start at any point, and go in a straight line, you eventually end up right back where you started.[br][br]P.S. This means Möbius strips have no inside or outside, which makes them non-orientable. This means any attempt to "invert" the Möbius strip results in the same structure you started with. In other words, Tony Stark is full of crap.