Vectores y Geometría en el espacio
Breve introducción a vectores y sistemas de coordenadas para espacios de tres dimensiones. Se verá que los vectores proveen una descripción particularmente simple de rectas y planos en el espacio.
Table des matières
- Sistemas de tres coordenadas
- Coordenadas
- Planos Coordenados
- Punto en el espacio
- Repaso
- Vectores
- Conceptos iniciales
- Operaciones Básicas
- Aplicaciones
- Repaso
- Producto Punto
- Definición
- Vectores Ortogonales
- Proyecciones
- Producto Cruz
- Definición
- Ortogonalidad
- Aplicaciones
- Proyecto
- Geometría de un Tetraedro
- Referencias
- Referencias
Coordenadas
A fin de representar puntos en el espacio, se elige primero un punto fijo O (el origen) y tres rectas que pasan por O que son perpendiculares entre sí, llamadas ejes de coordenadas y marcadas como eje x, eje y y eje z. Por lo común, se considera que los ejes x y y son horizontales, y que el eje z es vertical.
Conceptos iniciales
Observa y atiende el siguiente material relativo a los conceptos iniciales de vectores.
Definición
¿es posible multiplicar dos vectores de modo que su producto sea una cantidad[br]útil? Una respuesta es el producto punto, cuya definición se da a continuación.
Si [b]a[/b]=(a[sub]1[/sub],b[sub]1[/sub],c[sub]1[/sub]) y [b]b[/b]=(a[sub]2[/sub],b[sub]2[/sub],c[sub]2[/sub]), entonces el producto punto de [b]a[/b] y [b]b[/b] es el número dado por [b]a [/b]. [b]b[/b]:[br][br][b]a[/b] . [b]b[/b] = a[sub]1[/sub] b[sub]1[/sub] + a[sub]2[/sub] b[sub]2[/sub] + a[sub]3[/sub] b[sub]3[/sub]
Definición
Un vector perpendicular de a y b es el vactor resultante de la operación llamada producto cruz:[br][br]Si a=(a1,b1,c1) y b=(a2,b2,c2), entonces el producto cruz de a y b es el vector a x b:[br][br]a x b = (a[sub]2[/sub]b[sub]3[/sub] - a[sub]3[/sub]b[sub]2[/sub], a[sub]3[/sub]b[sub]1[/sub] - a[sub]1[/sub]b[sub]3[/sub], a[sub]1[/sub]b[sub]2[/sub] - a[sub]2[/sub]b[sub]1[/sub])
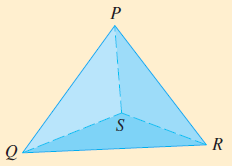
Geometría de un Tetraedro
Un tetraedro es un sólido con cuatro vértices P, Q, R y S, y cuatro caras triangulares.
Problema propuesto
Sean [b]v[sub]1[/sub][/b], [b]v[sub]2[/sub][/b], [b]v[sub]3[/sub][/b] y [b]v[sub]4[/sub][/b] vectores con longitudes iguales a las áreas de las caras opuestas a los[br]vértices P, Q, R y S, respectivamente, y direcciones perpendiculares a las caras respectivas[br]y que apuntan hacia afuera. Demuestre que[br][br][math]v_1+v_2+v_3+v_4=0[/math]
Referencias
- Marsden, Jerrold, Cálculo Vectorial, Addison Wesley, 2013.[br][br]- Stewart, Cálculo de Varias Variables, Cengage Learning, México, 2012.[br][br]- Nociones preliminares de física: Cálculo Vectorial, Escuela Técnica Superior de Náutica y Máquinas Navales, consultado en http://www.ehu.eus/juancarlos.gorostizaga/apoyo/vectores, 24 de Enero 2020.[br]