[b]Reconocimiento y proceso de resolución[/b][br]Para reconocer este caso de factorización debemos hacer lo siguiente:[br][br][list=1][*]Verificar que el polinomio se encuentre ordenado de forma descendente.[/*][*]Descartar que exista factor común[/*][*]Clasificar el número de términos que tiene el polinomio para ubicar el posible caso de factorización.[/*][*]Una vez que hemos identificado que el polinomio tiene 3 términos nos centramos en los casos únicamente para trinomios que hemos aprendido.[/*][/list][br][table][tr][td][b]TRINOMIO CUADRADO PERFECTO[/b][/td][td][b]TRINOMIO DE LA FORMA [/b][math]x^2+bx+c[/math][b][br]O TRINOMIO SIMPLE [br][/b][/td][td][b]TRINOMIO DE LA FORMA [/b][math]ax^2+bx+c[/math][b] O TRINOMIO COMPUESTO[/b][/td][/tr][tr][td][list][*]Primer termino y tercer término son cuadrados perfectos.[/*][*]Primer termino y tercer término tienen signo positivo.[br][/*][*]el segundo termino es el doble producto de la raíz cuadrada del primer termino por la raíz cuadrada del tercer término[/*][/list][br][/td][td][list][*]el coeficiente del primer término es igual a uno.[/*][/list][/td][td][list][*]el coeficiente del primer término es un número que por lo general no es cuadrado perfecto.[/*][/list][/td][/tr][tr][td]sino cumple con una de las 3 características descartado este caso.[/td][td]sino cumple con la característica , descartado este caso.[/td][td][br][/td][/tr][/table]

[b]TRABAJO EN CLASE 1: (TC1)[br][/b][br][list=1][*]Pasar la materia al cuaderno y resolver los siguientes ejercicios sección teoría.[/*][*]Subir un archivo de word con las fotos del trabajo resuelto a la carpeta compartida de la asignatura.[br]El archivo de word debe guardarse de la siguiente manera: Apellido y nombre-grado y paralelo-TC1 ejemplo. [br]Si el estudiante se llama Carlos Machado deberá guardar así: MachadoCarlos-9B-TC1.[br][br]Ejercicios:[br][br] [/*][/list]1. [math]4x^2-22x+30[/math][br][br]2. [math]9x^2-9x-28[/math][br][br]3. [math]2a^3+6a^2+4a^{ }[/math][br][br]4. [math]5x^2-18x+9[/math][br][br]5. [math]2x^2+15x+28[/math][br][br][br][br][br]

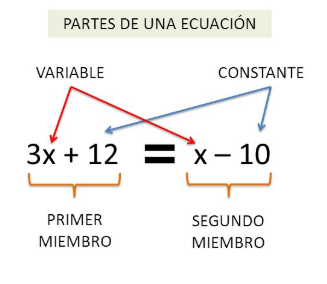
DESTREZA: M.4.1.10 Resolver ecuaciones de primer grado con una incógnita en ℤ en la solución de problemas.[br][br][b]Conceptualización:[/b][br][br][br][b]Ecuación:[/b] es una igualdad que contiene una incógnita o variable.[br][br]Sus partes son:

[b]Miembros: [/b]son las expresiones que se encuentra a cada lado del signo igual.[br][b]Incógnitas:[/b] es la letra o símbolo que se desconoce.[br][b]Coeficientes:[/b] son los valores numéricos (números) que multiplican a las incógnitas (están junto a las letras)[br][b]Términos independientes o constantes:[/b] son los valores o números que no están acompañados por las letras.

[b]Clasificación de las ecuaciones: [br][/b][br]Ecuaciones equivalentes.[br]Dos o más ecuaciones son equivalentes cuando tienen la misma solución.[br][br]Ejemplo:  Las ecuaciones siguientes son equivalentes:[br]a) 4x – 2 = 2x[br]b) 3x +1= x + 3    ya que ambas tienen por solución x = 1.[br][b]Por la variable:[/b][br][list][*]Enteras. La variable  está sumando, restando o multiplicando  3x + 4 = 1[/*][/list][list][*]Racionales: Alguna incógnita aparece en el denominador:  [/*][/list][list][*]Irracionales. Cuando ninguna incógnita aparece debajo del signo radical:[/*][/list][list][*]Exponenciales, logarítmicas y trigonométricas[/*][/list][br][b]Por el número de incógnitas:[/b][br][list][*]De una incógnita: 2x + 3 = 5x – 6[/*][/list][list][*]De dos incógnitas: 3x – 2y = 15[/*][/list][list][*]De tres incógnitas: 2x – y + 5z = 5[/*][/list][list][*]De [b]n[/b] incógnitas (en general)[/*][/list][br][b]Por el grado:[/b][br][list][*]Ecuaciones de primer grado o lineales. Cuando el mayor exponente con el que figura cualquier incógnita es uno: 3x – 2 = 7[/*][/list][list][*]Ecuaciones de segundo grado o cuadráticas. Cuando el mayor exponente con que figura cualquier incógnita es dos: 2x[sup]2 [/sup] + 3x – 5 = 0[/*][/list][list][*]Ecuaciones de grado n (en general): x[sup]5[/sup] + 2x[sup]2[/sup] – 3x + 1 = 0   sería de grado   5[/*][/list][br][b]Por el número de soluciones:[/b][br][list][*][b]Compatibles.[/b] Aquellas ecuaciones que tienen solución: Se dividen a su vez en:[/*][/list]                   - [b] Compatibles determinadas.[/b] Si tienen un número finito de soluciones.[br]                          x –2 = 0. Su solución es única, x = 2.[br]                          x[sup]2[/sup] – 9 = 0. Tiene dos soluciones, x = 3   y   x = – 3.[br]                   -  [b]Compatibles indeterminadas. [/b]Si tienen infinitas soluciones.[br]                         x + 2 = y. Tiene infinitas soluciones.[br][list][*][b]Incompatibles.[/b] Aquellas ecuaciones que no tienen solución: 2x – 1 = 2x + 3[/*][/list]    [br][b]PROPIEDADES DE LAS ECUACIONES[/b][br][br]Si a los dos miembros de una ecuación sumas o restas un mismo número o expresión, se obtienes otra ecuación equiva­lente a la dada.[br][br][b]De esta propiedad se deduce:[/b][br]En una ecuación puedes pasar un sumando de un miembro a otro cambiándolo de signo (se llama[b] transposición de términos[/b]). [br][br]Por ejemplo, [br][br]6x – 8 = 4 [br][br]6x = 4 + 8  [br][br]6x = 12[br][br]Cuando en los dos miembros de una ecuación aparecen términos iguales y con el mismo signo, se pueden suprimir. [br][br]Por ejemplo, [br]3x +2 – 5 = 4x – 5 [br][br]3x + 2 = 4x[br][br]Si multiplicas o divides los dos miembros de una ecuación por un mismo número o expresión distinta de cero, obtienes otra ecuación equivalente.[br]De la cual se deduce:[br][br][b]Para quitar los denominadores de una ecuación[/b] multiplica ambos miembros por el [b]m.c.m.[/b]  de todos los denominadores; obtendrás así otra ecuación equivalente sin denominadores.[br][br][b]Transposición de términos[/b][br]En una ecuación puedes pasar un término que está multiplicando al otro miembro dividiendo  y viceversa.[br]

[b]EJERCICIOS A RESOLVER[/b]

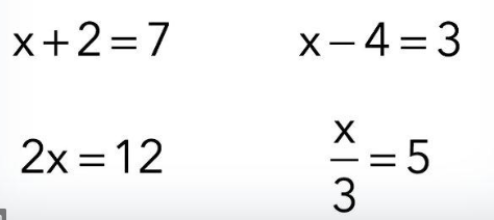
[b]PREGUNTAS[/b]

De los ejercicios de la imagen anterior trabajar con las siguientes instrucciones.[br]Instrucciones:[br][list=1][*]Pasar la materia al cuaderno. [/*][*]Identificar las partes de una ecuación, ejercicios propuestos[/*][/list]Rubrica de calificación:[br][table][tr][td][list][*]Materia pasada al cuaderno[/*][/list][/td][td]2[/td][td]puntos[/td][td][/td][td][/td][/tr][tr][td][list][*]Preguntas de repaso en el cuaderno[/*][/list][/td][td]4[/td][td]puntos[/td][td][/td][td][/td][/tr][tr][td][list][*]Ejercicios propuestos[/*][/list][/td][td]4[/td][td]puntos[/td][td][/td][td][/td][/tr][tr][td][/td][td][/td][td][/td][td][/td][td][/td][/tr][tr][td][/td][td][/td][td][/td][td][/td][td][/td][/tr][/table][color=#980000]Enviar las fotos de la materia en el cuaderno y de resolución de los ejercicios directamente a Idukay.[br]Las fotos del trabajo deben estar pegadas en un documento de word.[br][br][/color]El tiempo para envío del trabajo es jueves 26 de marzo.

[b][left]Tema: Dejando huellas para el cambio[/left]Subtema: [/b]Una función lineal hacia el cambio[br][br][b]¿Cómo graficar una función lineal?[br][/b][br]Primero, es necesario conocer con exactitud qué es un plano cartesiano: está formado por dos rectas[br]numéricas, una horizontal y otra vertical, que se cortan en un punto denominado eje de las abscisas (o[br]eje de las x ) y eje de las ordenadas (o eje de las y ). El punto donde se cortan se denomina origen.

[b]¿Cómo encontrar las coordenadas?[br][/b][br]1. Las coordenadas se forman siempre a partir de dos números, uno en cada eje ([b]xx[/b] y [b]yy[/b] ).[br]2. El primer número se busca en el eje de las [b]X[/b] y el segundo en el eje de las [b]Y[/b] .[br]3. Toma en cuenta los signos de los números de cada eje y los cuadrantes.

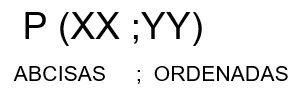
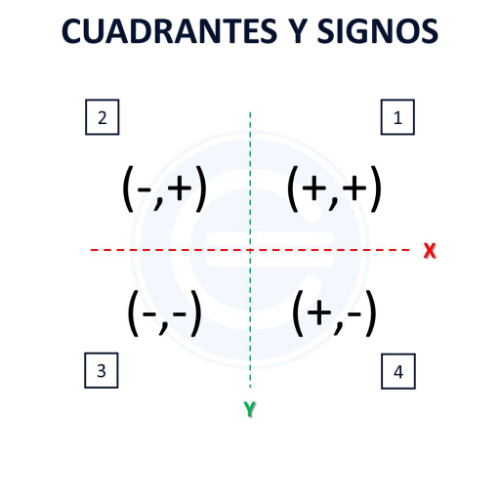
[b]Cuadrantes[/b][br]El primer cuadrante es[br]( [b]X[/b] Positivo, [b]Y[/b] Positivo), ubicado a la derecha en la parte superior. [br]El segundo cuadrante es[br]( [b]X[/b] Negativo, [b]Y[/b] Positivo), ubicado en la izquierda en la parte superior, junto al primer cuadrante.[br]Abajo del segundo cuadrante, tenemos ( [b]X[/b] Negativo y [b]Y[/b] Negativo). [br]El cuarto cuadrante está[br]ubicado a la derecha, junto al tercer cuadrante ( [b]X[/b] Positivo, [b]Y[/b] negativo).

[b]Función lineal con ecuaciones de primer grado[/b][br][br]Ejemplo: y=2x-1[br][br][list=1][*]Grafica una tabla. Propón valor para [b]X[/b] (recuerda puedes dar a [b]X[/b] valor desde cero hacia arriba o abajo). En base a esos valores, encontramos cuánto vale [b]y.[/b][/*][*]Usa la ecuación y= 2x-1. Crea otra tabla con dos columnas: una es la columna de las X y la otra de las Y . Reemplaza X con los valores propuestos a continuación en la columna designada. Resuelve la ecuación y coloca los resultados en la columna de las Y. Los pasos para seguir serían los siguientes:[/*][/list]

Dibuja la tabla y completa la columna de las X con los valores asignados. En este caso,[br]vamos a usar 5 valores en X:[br][table][tr][td][b]x[/b][/td][td][b]y[/b][/td][/tr][tr][td]-2[/td][td]-5[/td][/tr][tr][td]-1[/td][td]-3[/td][/tr][tr][td]0[/td][td]-1[/td][/tr][tr][td]1[/td][td]1[/td][/tr][tr][td]2[/td][td]3[/td][/tr][/table][br]Ahora calcula Y , utilizando la ecuación y = 2x – 1[br][br]Para esto utilizamos valor numérico.[br]