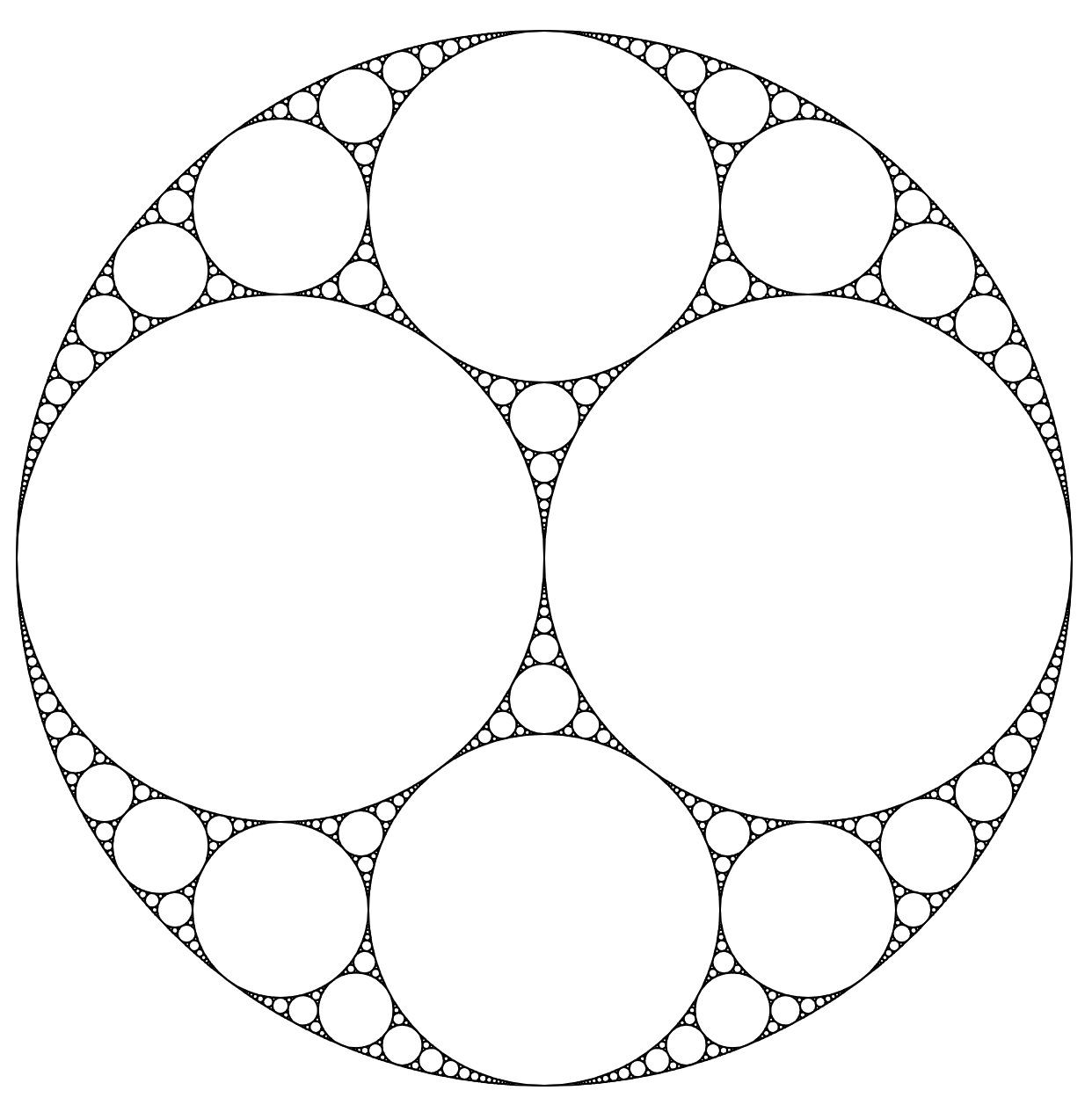
Apollonius-Kreise
Dieses Applet zeigt, wie das Apollonische Berührproblem von Kreisen mit Hilfe [br]von komplexen Zahlen und der Krümmungsformel von Descartes gelöst wird.[br]Ein Kreis ist mit Mittelpunkt z (komplex) und Radius r gegeben.[br]Die Krümmung k ist [math]\pm\frac{1}{r}[/math] u.z. positiv, wenn die Berührung außen erfolgt, ansonsten negativ.[br]Mit den angeführten "Berührformeln" kann man aus den Krümmungenk[sub]1[/sub], k[sub]2[/sub], k[sub]3[/sub] [br]den Wert k[sub]4[/sub] und damit den Radius r4, sowie aus den Mittelpunkten z[sub]1[/sub], z[sub]2[/sub], z[sub]3[/sub][br]die Mitte z[sub]4[/sub] ermitteln und damit auch weitere tangierende Kreise schmieden.[br]Eine Fortsetzung ergibt das Apolloniusnetz, wie man weiter unten sehen kann.
Ein Fortsetzung sieht dann, wie folgt, aus:
