Artistic heritage meets GeoGebra

Álvaro Martínez Sevilla, Jul 10, 2017

a closer view with GeoGebra to research on history of art and mathematics dissemination

Table of Contents

  1. The Mathematical Walks Project
    1. Description
    2. Objectives
    3. Directions
  2. Mathematics Dissemination
    1. Visual arithmetics
    2. The use of star polygons for representing sun rays
    3. Vectorial Calculus applied to sculpture
    4. Mathematical model on flowers in a vase
    5. 3D model on Mocárabes
  3. From maths to artistic interpretation
    1. Analysis on functionality of archs and lintels
    2. Looking center for pointed and multi centered archs
    3. Modelling to understand baroque lights and shades
    4. The Firsts algorithmic alphabets
  4. Research on History of Art
    1. The pattern construction
    2. The great number at the imperial palace
    3. The window that codifies Pi
  5. Discovering maths from art
    1. New Geometric Locus from a urbanistic problem
    2. New computational geometry problem from a romanic church

1.

The Mathematical Walks Project

[i][/i]

  • 1. Description
  • 2. Objectives
  • 3. Directions

1.1.

Description

[size=100][br][list][*][b]Dissemination activities:[/b] ERN, PiDay, Science weeks and fairs, Dissemination Congress, ...[br][/*][*][b]Mathematical Tourism [/b]entrepreneurship together with a scientific tourism business.[br][/*][*]A GeoGebra-based [b]printed Book + digital volume[/b]. More than 400 applets, together a disc with more monuments, mathematical concepts and the GGB files.[/*][*][b]Joint research[/b] on math and history of art.[/*][*][b]Working Team:[/b] 3 mathematicians, 1 art historian, plus the aid of scientific promotors.[/*][/list][/size]
Groups on Mathematical Walks
– Álvaro Martínez Sevilla

1.2.

–

1.3.

–

2.

Mathematics Dissemination

  • 1. Visual arithmetics
  • 2. The use of star polygons for representing sun rays
  • 3. Vectorial Calculus applied to sculpture
  • 4. Mathematical model on flowers in a vase
  • 5. 3D model on Mocárabes

2.1.

Visual arithmetics

Some consoles lets us to do some visual arithmetics[br][br]As [math]2\cdot\Phi=\sqrt{5}+1[/math] then [math]\Phi=\frac{\left(\sqrt{5}+1\right)}{2}[/math]
– Álvaro Martínez Sevilla

2.2.

–

2.3.

–

2.4.

–

2.5.

–

3.

From maths to artistic interpretation

  • 1. Analysis on functionality of archs and lintels
  • 2. Looking center for pointed and multi centered archs
  • 3. Modelling to understand baroque lights and shades
  • 4. The Firsts algorithmic alphabets

3.1.

Analysis on functionality of archs and lintels

We can analyze also over the sustentation on lintels and archs, and if the disposal of voussoirs are optimal or not.
Cathedral. Ecce Homo Gate
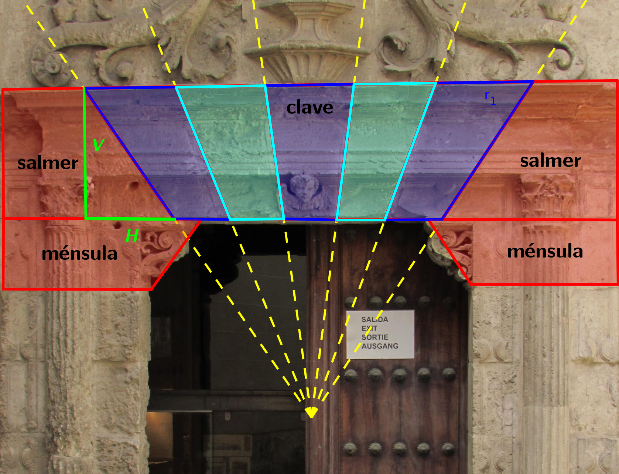
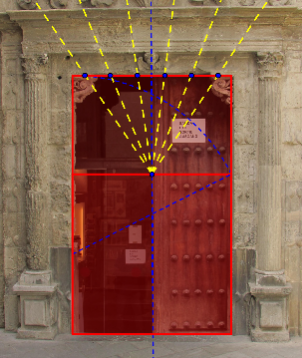
That [b]springing stone[/b] ([b][i]enjarje[/i][/b] on Spanish) is near optimal. Their surfaces receive almost perpendicular the forces transmitted by the arch
Silk Old Market. Granada
– Álvaro Martínez Sevilla

3.2.

–

3.3.

–

3.4.

–

4.

Research on History of Art

  • 1. The pattern construction
  • 2. The great number at the imperial palace
  • 3. The window that codifies Pi

4.1.

The pattern construction

Casa de Tiros. Granada
Is an enigmatic renaissance palace, with three polygons on bronze over the main door ([b]a triangle, a square and a octagon[/b]) never explained by historicians of art.[br][br]We found that it form part of a [b]triangular lattice[/b] that defines the facade, in the way of the great number defines some renaissance buildings on Italy, but with a completely singular geometry with many and rich artistic interpretations.
– Álvaro Martínez Sevilla

4.2.

–

4.3.

–

5.

Discovering maths from art

  • 1. New Geometric Locus from a urbanistic problem
  • 2. New computational geometry problem from a romanic church

5.1.

New Geometric Locus from a urbanistic problem

[size=100]At a main ceremonial gate, [b]La Puerta del Perdón[/b], of the Catedral of Granada, over a narrow street on the city, we may ask:[br][/size][br][b]Which is the correct distance to observe, at a glance (without scroll) that gate?[br][/b][br]The set of points from we can see the gate with a complete visual human angle (aprox 30 º) form a geometrical locus that is know as [b]Isoptic Curve of a segment[/b] (Arco Capaz on Spanish). This is historically associated to Pothenot Problem, and can be constructed with GeoGebra, taking in count both sides
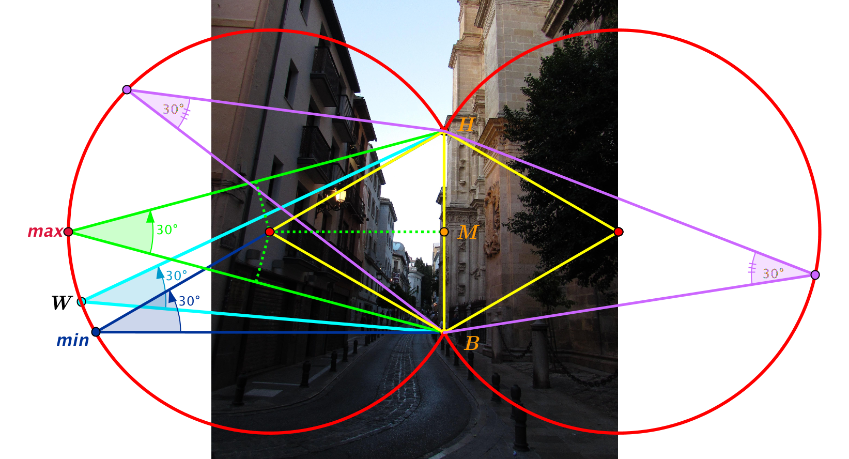
But, instead of taking the normal geometrical locus in GeoGebra for that problem, we can generalize this by asking[br][br][b]Which is the analogous geometrical locus if we count with an human vision angle ranging from 30º to 35º [/b](as occurs in fact)[b]?[/b][br][br]The result is a locus not described at the moment (as far as we know), that we called [b]Lunula Capaz[/b] (on spanish). And we can visualize it on GeoGebra activating the trace for the following construction.
– Álvaro Martínez Sevilla

5.2.

–

Information